基于遗传算法和人工神经网络的冷水机组模型参数辨识及误差补偿方法
张丽珠 章超波 陈琦 赵阳
(1 浙江大学制冷与低温研究所 杭州 310027;2 浙江省能源集团有限公司 杭州 310007)
作为中央空调系统的重要组成部分,冷水机组能耗约占中央空调系统的40%~50%[1]。由于冷水机组组成部件多且机理复杂,构建准确可靠的仿真模型往往较为困难。目前,已有许多学者对冷水机组仿真建模方法进行了研究,并开发了一些冷水机组性能模型。该领域早期研究关注于基于系统内部复杂热动力学方程的冷水机组建模方法。J.P.H.Bourdouxhe等[2]提出了ASHRAE Primary Toolkit 模型,该模型通过对冷凝器、蒸发器、压缩机和膨胀阀等组成部件分别建模,最终实现对冷水机组的整体建模。该类模型的构建难度较高,且系统的变工况特性需要反复迭代求解。该方面研究逐渐转向半经验或经验冷水机组仿真模型的研究。常见的半经验模型有Gordon-NG模型和Lee 模型,两者均通过对设备传热过程公式进行简化来得到关于冷水机组性能系数COP 的模型[3-4]。冷水机组经验模型主要包含简单一次线性回归模型(SL 模型)[5]、二次线性回归模型(BQ 模型)[6]、DOE-2 模型[7]和多元多项式回归模型(MP 模型)[8]。该类模型构建难度低且计算速度快,常被用于冷水机组性能预测和故障诊断[9]。此外,具有强大的非线性学习能力和较高的预测精度的人工神经网络等机器学习算法也开始被广泛应用于冷水机组建模[10-11]。
相比于上述几种方法,DOE-2 模型的输出包括冷水机组冷却水出口温度、冷冻水供水温度和功率,和实际仿真需求相符且具有一定的物理意义,因此被广泛应用于冷水机组仿真建模,DOE-2、EnergyPlus 和Dymola 等软件均采用了该模型。DOE-2 模型的参数通常采用最小二乘法对大量厂家性能数据进行拟合得到[12]。然而厂家性能数据往往很难获得。实际应用场景中传感器数量十分有限,很难通过最小二乘法直接拟合。同时由于实际中存在传感器偏差、模型假设不合理等问题,参数辨识得到的DOE-2 模型往往具有较大的预测误差。
本文提出一种基于遗传算法和人工神经网络的参数辨识和误差补偿方法解决上述问题,并在实际项目中进行验证,为可靠准确辨识冷水机组模型参数提供一种新思路。
1 模型参数辨识和误差补偿方法
1.1 DOE-2 模型
DOE-2 模型采用3 条性能曲线来预测冷水机组的出水温度和功耗[7]。这3 条曲线分别为制冷能力曲线、EIR 与运行状态关系曲线和EIR 与负载率关系曲线。其中EIR 为COP 的倒数,即轴功率与制冷量之比。制冷能力曲线用于计算冷水机组制冷量修正系数CAPFT,如式(1)所示。基于该修正系数,可以计算得到冷水机组最大可用制冷量,如式(2)所示。
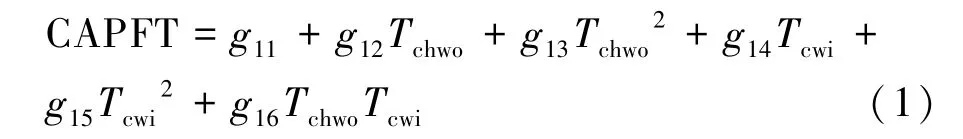
式中:Tchwo为冷冻水出口温度,℃;Tcwi为冷却水进口温度,℃;g11、g12、g13、g14、g15、g16为待定系数。

式中:CAP 为冷水机组的最大可用制冷量,kJ;Qr为冷水机组的额定制冷量,kJ。
EIR 与运行状态关系曲线用于计算满负荷运行时冷却水温度和冷冻水温度变化对冷水机组EIR 的修正系数,如式(3)所示。

式中:g21、g22、g23、g24、g25、g26为待定系数。
冷水机组部分负荷运行时,引入EIR 与负载率关系曲线,用于计算部分负荷修正系数EIRFPLR,如式(4)所示。
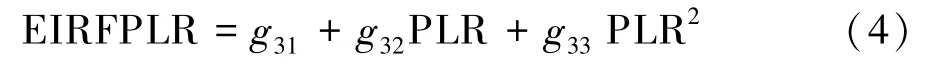
式中:g31、g32、g33为待定系数;PLR 为负载率,即冷冻水出口温度设定值下冷水机组制冷量Qs与所处工况下最大制冷量CAP 之比。
基于上述3 条性能曲线,最终可以计算得到冷水机组的实际功率,如式(5)所示。

式中:P为冷水机组实际功率,kW;COPr为冷水机组额定COP。
实际冷冻水出口温度由式(6)计算。

式中:Tchwo为冷冻水出口温度,℃;Qchw为冷组实际制冷量,kW,取Qs与CAP 的较小值。
实际冷却水出口温度由式(7)计算

式中:Tcwo为冷却水出口温度,℃;mcw为冷却水流量,kg/s;Qcw为冷却水吸收热量,kW,取P与Qchw之和。
1.2 基于外部知识库的遗传算法
遗传算法是一种常见的启发式寻优算法,已被广泛应用于模型参数辨识。通过合理设定约束条件缩小优化变量搜索范围,可以有效提高遗传算法计算效率。DOE-2 模型中3 条性能曲线的系数通常由实测数据拟合得到,模型参数所在范围无规律可循。如EnergyPlus、Dymola 和DOE-2 等仿真软件提供了麦克维尔、约克、开利和特灵等生产商不同型号冷水机组DOE-2 模型性能曲线系数。假设相似冷水机组之间性能曲线相近,那么通过已知冷水机组性能曲线系数可以快速确定待建模冷水机组DOE-2 模型参数搜索范围。基于这一假设,本文提出一种基于外部知识库的遗传算法,对建模冷水机组DOE-2 模型参数进行辨识,步骤如下:
1)确定目标函数。采用的目标函数如式(8)所示。遗传算法的最终目标为找到一组最优参数组合,使目标函数达到全局最小值。

式中:Tchwoi和Tcwoi分别为工况i下的实测冷冻水和冷却水出口温度,℃;和分别为工况i下DOE-2 模型预测的冷冻水和冷却水出口温度,℃;m为用于参数辨识的样本总量。
2)确定参数搜索范围。将Dymola 内部冷水机组DOE-2 模型性能曲线库作为外部知识库。在参数辨识过程中,首先通过对比该冷水机组与外部知识库中冷水机组在6 项指标上的相似度,找出外部知识库内与该冷水机组相似的所有冷水机组(以下称为参考冷机)。6 项指标分别为压缩机类型(离心式、螺杆式、活塞式等)、冷凝器类型(水冷式、风冷式等)、卸载机制(分级、进口导叶和变频器变频等)、生产商、性能曲线温度范围(冷冻水出口温度范围、冷却水进口温度范围)和额定制冷量。然后,根据参考冷机性能曲线系数确定DOE-2 模型参数搜索范围。本研究中取参考冷机性能曲线系数最大值和最小值作为参数寻优上下界。
3)基于上述目标函数和参数搜索范围,使用遗传算法对DOE-2 模型参数进行辨识。
1.3 基于人工神经网络的误差补偿方法
DOE-2 模型是一种近似拟合,误差来源十分广泛,往往很难用物理模型去描述。在此提出一种基于人工神经网络的误差补偿方法,基于其强大的非线性描述能力来对误差进行补偿。人工神经网络由输入层、隐藏层和输出层构成。每一层内部拥有若干神经元,相邻层间神经元通过权重相连。每一个隐藏层的神经元内部含有激活函数,用来提高神经网络的非线性拟合能力。人工神经网络内部权重可通过随机梯度下降[13]、Adam[14]等方法学习得到。
为了对DOE-2 模型进行误差补偿,需要对DOE-2 模型的输入和误差之间的映射关系进行学习。采用人工神经网络对DOE-2 模型的预测误差进行建模,并基于建立的模型对DOE-2 模型的误差进行补偿,如图1所示,具体步骤如下:
1)使用基于外部知识库的遗传算法对DOE-2 模型参数进行辨识,得到模型预测值。
2)根据实际数据,计算DOE-2 模型的预测误差。模型预测误差定义为:

式中:e为预测误差;y为实际值;为DOE-2 模型预测值。
3)训练DOE-2 模型误差的预测模型。本研究中人工神经模型的输入为DOE-2 模型的输入,输出为DOE-2 模型的预测误差,采用Adam 算法训练得到DOE-2 模型误差的预测模型。
4)将误差预测模型的输出加上DOE-2 模型的输出得到误差补偿后的DOE-2 模型(以下称为混合模型)的预测值:

式中:为混合模型预测值;为DOE-2 模型预测值;为DOE-2 模型误差预测值。

图1 冷水机组混合建模方法原理Fig.1 The schematic of the hybrid chiller modeling method
为了得到准确的人工神经网络模型,需要对神经网络的结构参数和超参数进行优化。根据Kolmogorov 定理,三层前向网络可以逼近任何连续函数[15]。因此,本研究中采用三层神经网络进行误差补偿。同时,该定理还给出了隐藏层神经元个数经验计算式,如式(11)所示[16]。采用该式计算神经网络隐藏层内部神经元个数。对于其他参数,例如激活函数和L2 正则化参数,采用交叉验证和网格搜索进行优化[17]。

式中:n为隐藏层节点数;p为输入层节点数。
1.4 模型性能验证指标
选用平均绝对误差(MAE)、平均绝对误差百分比(MAPE)、均方根误差(RMSE)、决定系数(R2)和均方根误差的变异系数(CV-RMSE)进行模型精度评估,定义如式(12)~式(16)所示。MAE、MAPE、RMSE 和CV-RMSE 反映了预测值和实际值之间偏离程度,值越小表明模型预测精度越高。R2反映模型的拟合程度,R2的值越接近1,说明模型对观测值的拟合程度越好。

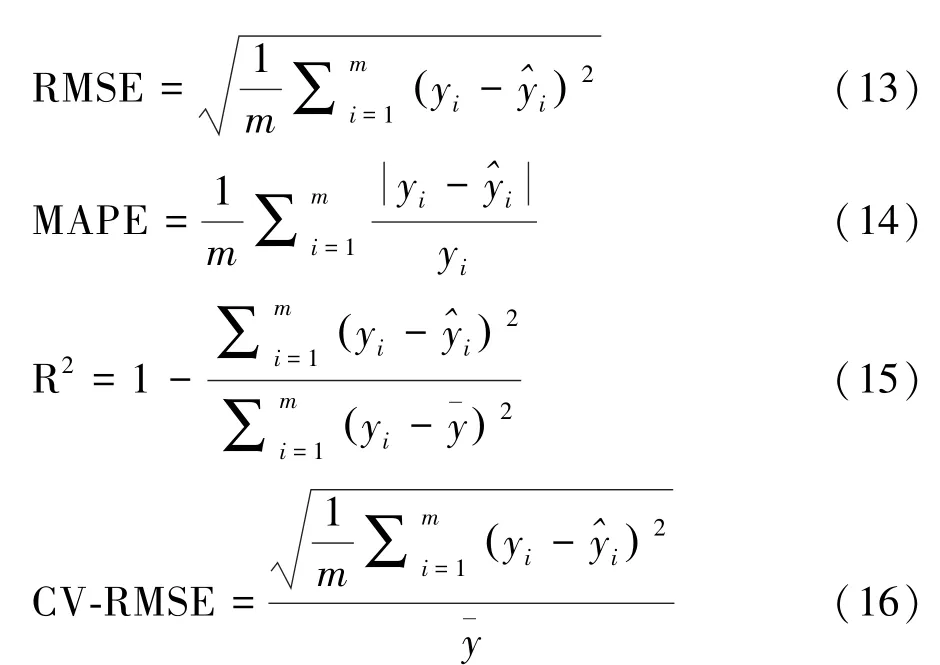
式中:为模型预测值;yi为实际值;为实际值的平均数;m为总样本数。
2 仿真验证
2.1 验证数据集
采用一台实际离心式冷水机组(额定制冷量为5 275 kW)的实测数据集对提出的方法进行验证。数据采集时间段为2019-05-11—2019-11-14,采样频率为5 min/次,共获得27 918 组样本。被测变量包括冷水机组冷冻水进出口温度、冷却水进出口温度、冷冻水供水温度设定值、冷冻水流量和冷却水流量。各被测变量的箱线图如图2所示。随机抽取70%的数据作为训练集,30%的数据作为测试集。训练集用作模型训练,测试集用作模型性能验证。

图2 被测变量箱线图Fig.2 Box plots of the measured variables
2.2 基于外部知识库的遗传算法性能评估
该冷水机组的压缩机类型为离心式,冷凝器类型为水冷式,卸载机制是通过进口导叶开度调节制冷量,额定制冷量为5 275 kW。由图2 可知,冷冻水出口温度通常位于8.4 ℃附近,冷却水进口温度通常位于29.4 ℃附近。基于该冷水机组的以上6 项指标,最终从Dymola 冷水机组性能曲线库筛选得到5 台与其相似的冷水机组作为参考冷机。参考冷机各项指标如表1所示,表中所有冷机的生产商均为开利,采用离心式压缩机,水冷式冷凝器,卸载机制为进口导叶。取参考冷机性能曲线系数的最大值和最小值分别作为对应参数寻优范围的上下边界,如表2所示。

表1 参考冷机的各项指标Tab.1 Performance indexes of the reference chillers

表2 遗传算法参数寻优范围上下界Tab.2 Parameter bounds for the genetic algorithm
利用MATLAB 遗传工具箱在训练集上对该冷水机组DOE-2 模型进行参数辨识。通过引入各参数搜索范围均为-1~1 作为对照组,对基于外部知识库的遗传算法参数辨识性能进行评估。由于遗传算法寻优具有随机性,在有知识库和无知识库情况下分别进行5 次寻优。遗传算法迭代次数和模型精度如图3所示。结果表明:基于外部知识库的遗传算法可以大大提高模型参数辨识效率,并提高模型精度。在无外部知识库的情况下,遗传算法的迭代次数在217~462次内波动,模型在训练集上的误差在1.40~1.44 ℃2内波动。在有外部知识库的情况下,遗传算法迭代次数显著降低(在79~136 次内波动),而模型误差显著减小(在0.260~0.263 ℃2之间)。

图3 有无知识库的遗传算法性能对比Fig.3 Performance comparisons between genetic algorithms with and without a prior knowledge base
辨识后DOE-2 模型的预测值与实测值在测试集上的对比结果如图4 和图5所示。由图4 可知,存在部分冷冻水出口温度的预测值与实际值相差较大的情况,说明DOE-2 模型不能很好地预测该冷水机组在所有工况下的冷冻水出口温度。对于冷却水出口温度,图5 显示DOE-2 模型能很好预测该冷水机组的冷却水出口温度,绝大部分冷却水出口温度的预测值与实际值之间的相对误差绝对值均小于5%。DOE-2 模型在测试集上的预测精度如表3所示。结果表明:DOE-2 模型对该冷水机组冷冻水出口温度整体预测精度远远小于冷却水出口温度。
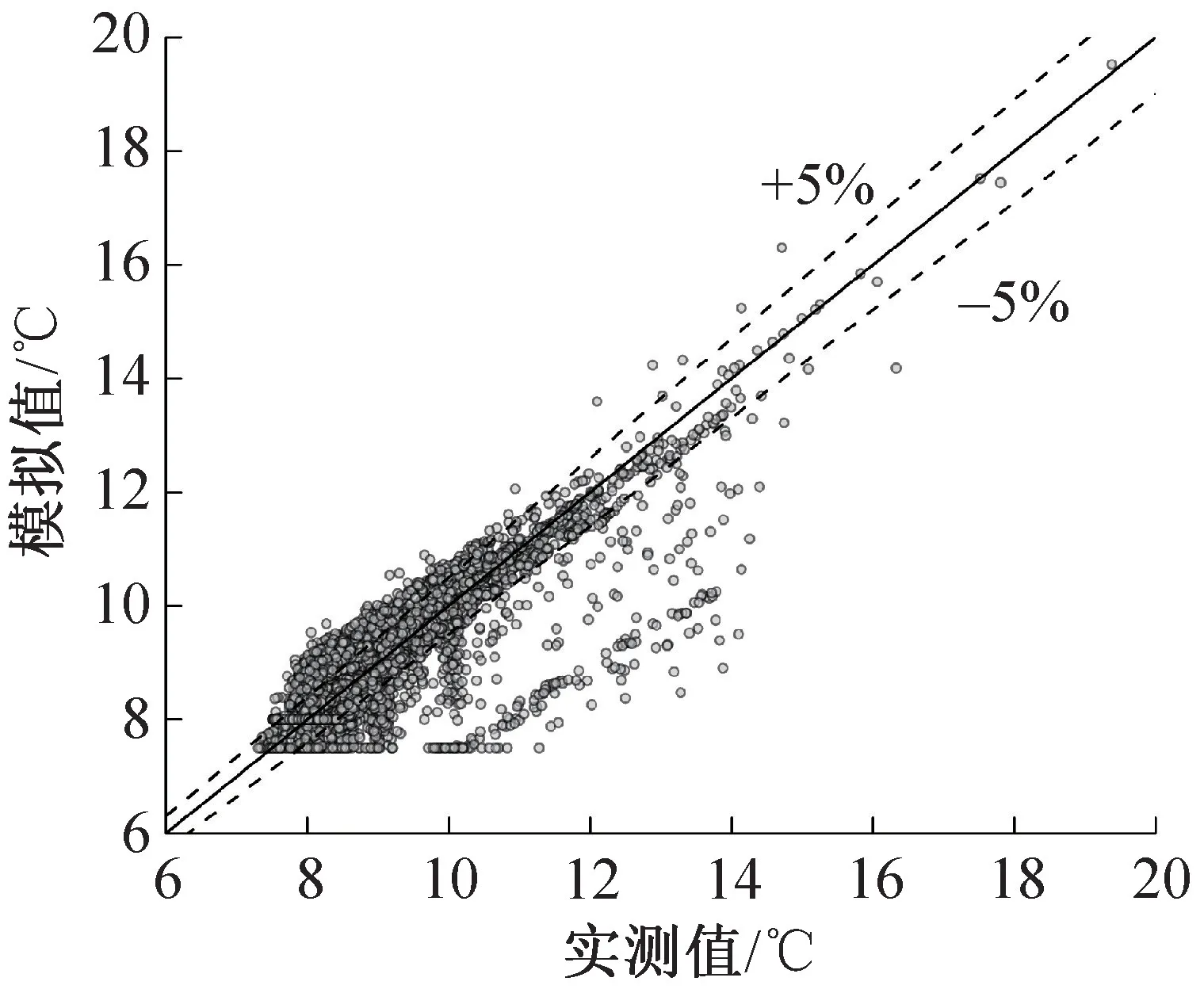
图4 DOE-2 模型冷冻水出口温度预测值与实测值对比Fig.4 Comparisons between the predicted and measured chilled water outlet temperatures
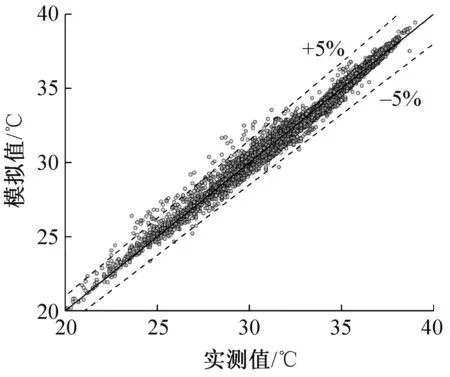
图5 DOE-2 模型冷却水出口温度预测值与实测值对比Fig.5 Comparisons between the predicted and measured cooling water outlet temperatures

表3 DOE-2 模型在测试集上的精度Tab.3 Accuracy of the DOE-2 model on the testing set
精度指标冷冻水出口温度冷却水出口温度
综上所述,冷水机组冷冻水出口温度预测值与实测值误差较大,无法满足实际要求。分析原因可能是传感器漂移、传感器测量误差、模型假设不合理、遗传算法参数寻优的不确定性等。
2.3 基于人工神经网络的DOE-2 模型误差补偿方法性能评估
为了补偿DOE-2 模型在预测冷冻水出口温度时的误差,采用三层人工神经网络对冷冻水出口温度预测误差进行建模。模型的输入与DOE-2 模型保持一致,输出为冷冻水出口温度预测误差。
采用网格搜索和5 折交叉验证方法优化冷冻水出口温度误差补偿模型的激活函数和L2 正则化参数。优化结果如表4所示。激活函数的最优解为relu 函数,L2 正则化参数的最优解为0.001。模型训练采用Adam 算法。

表4 误差补偿模型最优超参数Tab.4 Optimal hyper-parameters of artificial neural networks for error compensation
基于训练得到的误差补偿模型,对DOE-2 模型的冷冻水出口温度预测值进行校准。混合模型在测试集上的预测效果如图6所示。相比于DOE-2 模型(图4),混合模型冷冻水出口温度预测值与实际值更加接近,绝大部分出口温度预测值与实际值之间的相对误差绝对值小于5%。
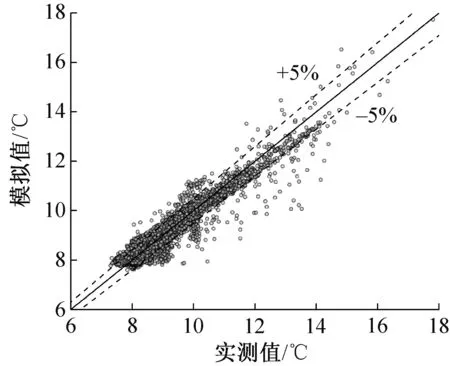
图6 混合模型冷冻水出水温度预测值与实测值对比Fig.6 Comparisons between the corrected and measured chilled water outlet temperatures
人工神经网络也能够直接用来预测冷冻水出口温度和冷却水出口温度。因此,本文进一步对比了人工神经网络与混合模型和DOE-2 模型之间的预测精度。同样采用网格搜索和5 折交叉验证方法优化人工神经网络模型的激活函数和L2 正则化参数。最优结果如表5所示。模型训练采用Adam 算法。混合模型、DOE-2 模型和人工神经网络模型在测试集上的预测精度如表6所示。结果表明:混合模型相比于DOE-2 模型或人工神经网络模型具有更高的精度。相比于DOE-2 模型,混合模型在预测冷冻水出口温度时的MAE、RMSE、MAPE 和CV-RMSE 分别降低了36.49%、46.00%、33.16%和45.73%,R2提高了25.75%。

表5 人工神经网络模型最优超参数Tab.5 Optimal hyper-parameters of the artificial neural network-based chiller model

表6 各模型冷冻水出口温度预测精度对比Tab.6 Prediction accuracy of the chilled water outlet temperature of the three types of models
3 结论
本文提出了一种基于遗传算法和人工神经网络的冷水机组模型参数辨识及误差补偿方法,并利用某离心式冷水机组的实际运行数据对提出的方法进行了验证。通过建立冷水机组DOE-2 模型,研究了有知识库和无知识库情况下遗传算法参数辨识的性能,并采用人工神经网络方法构建了冷冻水出口温度误差补偿模型,对比了有补偿和无补偿情况下DOE-2模型的精度。得到如下结论:
1)基于外部知识库的遗传算法在进行DOE-2 模型参数辨识时具有更高的效率和精度。无外部知识库的情况下,遗传算法的迭代次数范围为217~462次,模型在训练集上的误差在1.40~1.44 ℃2之间。在有外部知识库的情况下,遗传算法的迭代次数范围为79~136 次,在训练集上的误差在0.260~0.263℃2之间。
2)得到的DOE-2 模型对该冷水机组冷冻水出口温度预测精度远远小于冷却水出口温度。绝大多数冷却水出口温度预测值与实测值的相对误差均能保持在5%以内。但对于冷冻水出口温度,存在部分工况下冷冻水出口温度的预测值与实际值相差较大的情况。
3)相比于DOE-2 模型和人工神经网络模型,本文提出的混合模型具有更高的预测精度。相比于DOE-2 模型,其在预测冷冻水出口温度时的MAE、RMSE、 MAPE 和 CV-RMSE 分别降低 36.49%、46.00%、33.16%和45.73%,R2提高25.75%。

