喷射器及其在制冷中的应用研究进展
陈光明 孙翔 宣永梅 高能 郝新月
(1 浙江大学制冷与低温研究所 杭州 310007;2 浙大宁波理工学院能源与环境研究所 宁波 315100)
随着工业发展、城市化进程的加快,人们对能源的需求越来越大。随之而来的能源短缺、价格上涨以及全球性的环境问题,使得研究人员转向对可再生能源的研究,并考虑优先利用低品位能源、提高能源利用效率。
喷射器是一种可以利用高压流体引射低压流体,有效利用流体压力能的部件,最早的研究开始于在19世纪60年代[1]。1901年,K.Chunnanond 等[2]将喷射器用于抽除蒸汽冷凝器中的不凝性气体。当时喷射器主要用于蒸汽机领域,代替机械泵给锅炉加水,喷射制冷循还没有提出。经历了一个多世纪的发展,如今喷射器作为一种具有升压、节流、泵送、混合等多功能的部件已经被广泛应用。
本文将对喷射器的工作机理、性能评价指标、理论模型建立、结构尺寸对性能的影响以及喷射器在制冷中的应用等方面的研究进展进行介绍。
1 工作机理及评价指标
1.1 喷射器的工作机理
喷射器按喷嘴出口截面工作流体的速度大小可分为亚音速喷射器与超音速喷射器。超音速的物理过程是指流体的实际流速大于流体所处状态时声音传播速度的流动过程;反之,实际流速小于流体所处状态时声音传播速度的流动过程为亚音速流动。本文主要介绍超音速喷射器。
图1 是一个超音速喷射器内部结构工作机理示意图。喷射器可分为喷嘴、接受室、恒面积段和扩压段四部分,喷射器的工作机理为:高压(高于相应临界流动的滞止压力)的工作流体依次经过喷嘴的渐缩、渐扩段,速度在喷嘴喉部到达音速,在喷嘴出口截面到达超音速。在此过程中,工作流体的压力降低,压力能转换为动能。喷嘴出口的工作流体凭借其较低的静压,与引射流体入口之间形成压差,驱动引射流体进入接受室。随后二者混合,在混合过程中发生剧烈的质量、动量、能量交换,混合流体速度由超音速降为亚音速时,还会出现激波现象,压力升高,进入扩压室。在扩压室内,混合流体动能转换为压力能,最终从喷射器出口排出,实现了把引射流体压力升高的目的。
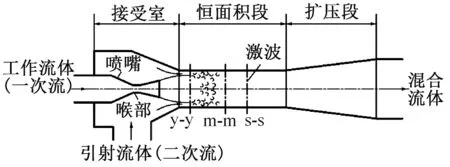
图1 喷射器内部结构工作机理[3]Fig.1 Principle of ejector configuration[3]
1.2 喷射器性能的评价指标
喷射器的性能评价指标[3]主要有:喷射系数、压缩比、膨胀比、喷射器效率等。喷射制冷系统评价指标有:系统制冷量、COP 等。
喷射系数是对喷射器引射能力的评估,可以被定义为喷射器引射流体与工作流体的质量流量之比。

式中:me为引射流体的质量流量,kg/s;mg为工作流体的质量流量,kg/s。
压缩比被定义为喷射器出口混合流体与引射流体的压力之比。

式中:pc为喷射器出口混合流体的静压力,kPa;pe为引射流体的静压力,kPa。
膨胀比被定义为喷射器进口的工作流体压力与喷射器接受室前的引射流体压力之比。

式中:pg为喷射器进口工作流体的静压力,kPa;pe为引射流体的静压力,kPa。
索科洛夫等[4]指出,喷射器的完善性可用喷射器效率来衡量,即引射流体获得的与工作流体丧失的之比。

式中:eg、ec、ee分别为工作、混合、引射流体的单位,kJ/kg。

式中:h0、s0为等熵滞止状态下工质的比焓、比熵,kJ/kg、kJ/(kg·K);h0,e、s0,e为与周围环境处于平衡状态下工质的比焓、比熵,kJ/kg、kJ/(kg·K);T0,e为环境温度,K,通常取293 K。
S.Elbel 等[5]提出了喷射器对功的恢复效率,同时考虑了引射流量和压力提升的影响。他们把喷射器效率定义为实际能从喷射器中恢复的能量的比例,即从接受室入口到扩压室出口引射流体被等熵压缩的功除以从喷嘴进口到扩压室出口理论上工作流体可以被回收的最大能量。
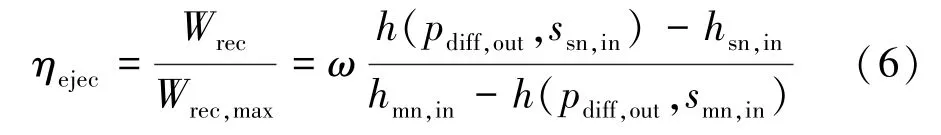
式中:ω为喷射系数;h为引射流体经等熵压缩在扩压室出口的比焓,kJ/kg;hsn,in为引射流体接受室入口的比焓,kJ/kg;hmn,in为工作流体喷嘴入口的比焓,kJ/kg;h(pdiff,out,smn,in)为工作流体经等熵膨胀在扩压室出口的比焓,kJ/kg。
上述性能指标中,喷射系数是最直接、最容易理解的指标,反映了通过消耗一定数量的工作流体来获得一定数量引射流体的压力提升,但是没能反映流体所携带能量的价值。索科洛夫等[4]的效率虽然试图反映流体的能量问题,但是由于概念本身存在的缺陷,例如基准态问题,使得它难以得到实际使用;更为严重的是,它忽视了混合过程是喷射器的本质特征,把工作流体与引射流体分开单独考虑,因此它不能真实反映喷射器的实际工作过程。文献[5]所提出的喷射器对功的恢复效率虽然克服了效率所存在的缺陷,但同样没有反映混合过程是喷射器的本质特征,因此也不能真实反映喷射器的实际工作过程。
本文作者认为,要建立合理的喷射器性能评价指标,首先要建立能够反映喷射器本质特征的理想喷射器模型,用实际喷射器的性能与理想喷射器的性能接近的程度作为评价实际喷射器优劣的指标,才有理论和实际价值。
2 理论模型进展
本节将介绍喷射器理论模型的研究进展。所涉及的模型假设有:工质为理想气体、喷射器边界绝热、入口速度为零、径向温度与速度均匀分布等。其他常见的模型简化手段包括:恒压或恒面积混合假设、将斜激波近似为正激波、引入等熵效率系数来近似每段的损失、假设两相混合物性质均匀以及在工作流体形成的有效面积喉部开始混合。
1942年,J.H.Keenan 等[6]最先提出了基于理想气体动力学理论的喷射器一维数学模型,研究的是一个简化的恒面积混合的喷射器,且不包含扩压段。其假设包括:工质为理想气体、喷射器边界绝热、流动为等熵过程,入口速度为零,此外还讨论了正激波现象。1950年,J.H.Keenan 等[7]在之前研究的基础上考虑了喷射器的多种几何结构,包括不同的喷嘴和混合段尺寸,其模型将喷射器分为4 个基本的子部件:喷嘴、接受室、混合室和扩压室。基于以上假设,结合动量、能量和质量守恒方程,即可确定各子部件关键界面工质的参数。
J.T.Munday 等[8]假设工作流体从喷嘴喷出后,并不立即与引射流体混合,而是为引射流体形成一个收敛管道,该管道就像一个收敛的喷嘴,这样引射流体在某个位置加速到音速,该位置即为喉部,如图2所示[8-10]。在此之后,两股流体在相同的压力下发生混合。

图2 喷射器假想有效面积Fig.2 Effective area occurring in the ejector throat
J.C.Dutton 等[11]对恒面积混合的超声速喷射器进行了理论和实验研究,理论分析了基于简化的恒面积混合且无黏滞力相互作用的一维模型。研究了7个无因次变量对喷射器压力恢复性能,即压缩比的影响。实验结果表明,理论预测的喷射器最大压缩比较实验值高15%~22%。该误差很大程度上是由于模型忽略了流动过程中的摩擦损失。
在Keenan 模型的基础上,I.W.Eames 等[12]进行了模型的一项重要改进,考虑了喷嘴、混合段和扩压段的摩擦损失,在计算质量、动量、能量守恒时计入了基于实验数据的等熵效率经验系数。
Huang B.J.等[3]也提出过类似的模型,同样假设工质为理想气体,且考虑到摩擦和混合损失而采用等熵效率系数。以R141b 为工质,在多种工况下对11种不同几何结构的喷射器进行了实验测试,该理论模型采用的等熵效率系数基于相同工况下的实验数据。
Huang B.J.等[13]研究了壅塞现象对喷射器性能的影响,绘制了背压对喷射系数的影响曲线。如图3所示[3],发生压力与蒸发压力保持不变,其中喷射器的运行模式分为3 种:临界(双壅塞)、亚临界(单壅塞)和回流模式。当背压低于临界背压,喷射系数是恒定的,达到极大值,临界模式下工作流体与引射流体均发生壅塞;当背压大于临界背压而小于极限背压,喷射系数随背压的增大而减小,此时为亚临界模式,仅工作流体发生壅塞;当背压大于极限背压,喷射系数为0,即回流模式下喷射器无法工作。他们详细阐述了临界模式下恒压混合喷射器的一维模型。该模型假设开始混合截面位于恒面积段内,而且引射流体达到音速,然后工作流体与引射流体在相同的压力下进行混合。有学者在此基础上进行了修改,得到更准确的结果[14-15]。

图3 喷射器的运行模式Fig.3 Operational modes of ejector
Liu Jiapeng 等[16]在Huang B.J.等的基础上提出了进一步简化的模型。用含有4 个参数的两个线性方程来求解喷射系数与临界背压,而4 个参数可通过等熵效率系数以及几何尺寸参数得到。为了简化理论模型,假设了喷射器各部件的等熵效率不随工况条件和几何参数的变化而变化。对比文献中可用的实验值,结果显示喷射系数和临界背压的平均误差分别为3.13%和1.35%。Zhang Hailun 等[17]借助CFD 研究了不同粗糙度对喷射器整体以及各部件效率的影响,为模型部件效率的选择提供了参考。
Zhu Yinhai 等[18]提出了一种喷射器临界模式下同时考虑流向与径向的临界圆二维模型。见图4,在恒面积段入口截面引入“临界圆”,采用指数式来近似该截面流体的径向二维速度分布。作者对模型进行了实验验证。结果显示,实验与理论结果的最大误差为10.78%,而Huang B.J.等[3]一维模型的误差为23%。此外,Zhu Yinhai 等的模型只需要14 个方程和2 个等熵系数,而Huang B.J.等的模型需要18 个方程和4 个等熵系数。Zhu Yinhai 等[19]基于上述模型还研究了两相工质模型。但为了简化研究,他们假设工作流体和引射流体的径向速度分布为线性而非指数。

图4 喷射器结构与A-A 截面流场Fig.4 Configuration of ejector and A-A section flow field
N.S.Kumar 等[20]基于法诺流动和可变热容比,对一维喷射器模型进行了修正。利用法诺流动方程来描述混合段的可压缩摩擦流动。此外,考虑到热容比在喷射器每段的差异,引入热容比在各段的平均值进行计算,而不是假设一个恒定的值。与传统一维模型相比,该修正模型得到的喷射系数、背压的平均误差分别为4%和5%,具有更高的精度。
涉及亚临界模式下的喷射器模型研究文献较少。传统的喷射器模型侧重于研究理想运行工况,即临界模式下的性能。受客观因素影响,在某些情况下,喷射器未必能在临界模式下稳定运行,因此对于亚临界模式的研究具有重要意义。Chen Weixiong 等[21]研究了临界、亚临界模式下的一维喷射器模型。亚临界模式下,仍假设喷射器内壁与工作流体之间仍然存在一个有效面积区域,此处引射流体被加速至最大速度,但低于声速,未达到壅塞状态。除了该有效区域处的控制方程与临界模式不同外,其他方程相同。Shi Chaoyin 等[22]提出了工质为实际气体的临界与亚临界模式下的一维喷射器模型。对于亚临界模式,采用了与Chen Weixiong 等[21]相同的边界条件。
Li Fenglei 等[23]也提出了预测亚临界模式下喷射器性能的模型。该模型基于恒压混合等假设,可预测临界背压、极限背压和喷射系数。随着背压超过临界值,喷射系数呈线性下降,在引射流体流量为零的情况下,结合质量、动量和能量守恒方程和等熵关系可以得到极限背压值。
V.Kumar 等[24]提出了一种新型的一维模型。模型引入Prandtl 混合长度、Prandtl-Meyer 膨胀波、Kelvin-Helmholtz 不稳定性和斜压效应等气体动力学概念来确定各个截面的直径、混合段长度、喷嘴出口位置、喷嘴收敛角和发散角。结果表明,与Huang B.J.等[3]的一维模型相比,二者面积比、喷射系数的偏差分别为-0.287%、2.5%。
为了解决1.2 节评价指标的问题,一些研究者提出了理想喷射器模型。
根据喷射器的工作特点,A.Arbel 等[25]提出了理想膨胀压缩机(Turbine-compressor)模型,以此作为实际喷射器内部损失的比较基准。R.K.Mcgovern等[26]根据可逆过程能效最高的热力学常识,将喷射器作为“黑箱”,假设在“黑箱”内发生的所有过程均为可逆过程,称之为可逆喷射器并进行了分析。以理想膨胀压缩机模型为基础,进一步引入理想热机概念以实现膨胀机、压缩机排出流体之间温度的一致。虽然这些模型试图给出喷射器的最高能效以作为实际喷射器的比较基准,然而忽视了一个最基本、最重要的事实,即实际喷射器不是通过功的传递来实现低压流体压力的提升,而是通过混合过程中动量的交换实现能量的传递,即实际喷射器不存在任何机械运动部件,也就不存在任何机械功的传递过程。混合过程动量交换是喷射器所具有的、区别于其他能量交换设备的本质特征,任何忽视这一特征的模型都不能真正反映喷射器的本质;此外,实际喷射器的混合压力远低于其出口压力,而以“膨胀压缩机”为基础的模型都认为混合压力等于出口压力。因此此类模型偏离实际喷射器的工作机理太远,不仅不能指导实际喷射器能效的提高,甚至可能产生严重的误导。
3 结构尺寸的影响
喷射器作为系统中的关键部件,其性能对系统效率有着重要的影响,越来越多的研究关注于喷射器几何形状和运行工况对系统性能的影响。本节重点关注喷射器几何尺寸对系统性能的影响。从理论上来说,不同的运行工况对应不同的喷射器最佳结构。
3.1 喷嘴
对于超音速喷射器来说,喷嘴相关的几何尺寸包括:喷嘴出口位置、喷嘴收敛角、发散角、喷嘴收敛段、喉部、发散段长度。
如图5所示,根据喷射器喷嘴出口与恒面积直管段的入口对应位置关系,通常将喷射器分成两类,文献称之恒压混合喷射器和恒面积混合喷射器。

图5 喷射器结构区别Fig.5 Different structure of ejector
此处分类只是依据喷射器的结构特征而提出的,与喷射器理论模型中所说的恒压混合模型以及恒面积混合模型不同。恒压混合模型是指混合过程动量方程中所用的压力为恒定值,而恒面积混合模型是指在混合过程动量方程中流动方向上的横截面的面积保持不变。J.H.Keenan 等[7]最早提出恒压混合喷射器的概念,J.T.Munday 等[8]提出恒压混合模型,J.H.Keenan 等[6]提出恒面积混合模型,而Huang B.J.等[3]提出的喷射器结构上是恒面积混合喷射器,但混合模型却采用恒压混合模型。
喷嘴出口位置对喷射器的性能有较大影响。对于固定结构的喷射器,通常是根据设计工况,按经验确定喷嘴位置。但当运行工况偏离设计工况时,此时的喷嘴位置往往不能提供较好的喷射器性能。S.Aphornratana 等[27]首次提出可移动喷嘴的设计,即喷嘴可在混合室内轴向移动,研究了喷嘴位置对系统制冷量和性能系数的影响,结果表明这种喷射器具有良好的变工况适应性。R.Yapici[28]进行了一种可移动喷嘴喷射制冷系统的实验研究。结果表明,最佳的喷嘴出口位置在距恒面积段进口上游5 mm 处。K.Chunnanond 等[29]通过实验发现,将喷嘴引回恒面积段外,即喷嘴向喷射器上游移动,可以减小膨胀波的膨胀角,更多的引射流体通过由此产生的更长的夹带管段进入恒面积段,从而提高喷射器的性能。另一方面,引射流体的增多使得混合流体的动量降低,激波位置向上游偏移,喷射器不得不在较低的背压下工作。Chen Shaojie 等[30]以R236fa 为工质从理论与实验上对可移动喷嘴的喷射器性能进行了研究,其通过实验研究了喷嘴位置对喷射器临界模式下的喷射系数的影响,发现临界喷射系数随喷嘴出口与恒面积段入口距离的增加先增大后不变。因此在一定范围内,临界喷射系数取决于引射流体的壅塞情况。当喷嘴向上游移动时,混合流体在恒面积段内达到声速,临界喷射系数保持不变。Wang Chen 等[31]提出了一种自适应喷嘴结构的喷射器,即在喷嘴上安装波纹管,喷嘴位置可根据工作压力的变化而改变,波纹管的设计基于数值模拟的结果。Fu Weina 等[32]数值研究了喷嘴出口位置的影响。结果表明,当喷嘴出口至恒面积段进口距离与喷嘴喉部直径的比值从0 增至19时,喷射系数持续增大;当该比值继续增大,喷射系数急剧下降,此时喷嘴出口截面位于混合室收敛段进口的上游。此时工作流体在喷嘴出口膨胀较剧烈,导致引射流体流动有效面积减小,从而导致喷射系数骤降。史海路等[33]实验研究了喷嘴出口位置的影响,结果均显示存在最佳位置使得喷射系数最大。最佳喷嘴出口位置值还会随着其他几何尺寸的变化而变化[14,34]。
Wang Lei 等[35]利用CFD 数值研究了喷嘴的收敛角和发散角,喷嘴收敛段、喉部和发散段长度对喷射器性能的影响。随着喷嘴收敛角的增大,工作流体流量与喷射系数先缓慢增大再急剧下降;随着喷嘴发散角的增大,工作流体流量与喷射系数先急剧上升再缓慢下降;随着喷嘴收敛段、喉部和发散段长度的增加,喷射系数先增大后减小。在其所研究的几个几何因素中,喷嘴喉部和发散段尺寸对喷射系数的影响较大。姚轶智等[36]通过在喷嘴尾部设置静态扰流元件,拓展混合空间以增强动量交换效率的同时将传统的动量交换过程由二维变为三维,在亚音速工况下提升了喷射器喷射系数,但临界压力降低。薛康康等[37]提出采用花瓣形喷嘴提高混合效率的方法提升了喷射器性能,数值结果表明,与圆形喷嘴相比,该结构下的临界背压提高了5%,喷射系数最多可提高13.3%。
3.2 接受室
接受室收敛角是影响喷射器性能的重要参数之一。Wu Hongqiang 等[38]研究了恒压混合下接受室收敛角θ对引射系数的影响。收敛角较小时,喷射系数随θ的增大而增加,当θ介于8~10°时,达到最大值,之后随θ增大缓慢减小。因此,对于给定长度的混合室,存在一个最佳的接受室收敛角。当收敛角大于最佳收敛角时,作者通过CFD 解释了此时喷射系数减小的原因,即随着收敛角的增大,喷射器内涡流的分布更加明显,从而降低了喷射器性能。
A.S.Ramesh 等[39]从数值模拟与实验上对收敛角介于0~22°的6 个不同尺寸喷射器进行了研究。结果表明,在所研究的工况下,收敛角12°的喷射器对应的喷射系数最佳,与收敛角0°对应的最佳喷射系数相比,增加了99.1%。
但是,对于不同的喷射器类型、不同的工质、不同的运行工况,最佳收敛角的值往往不同[40-44]。
3.3 恒面积段
面积比是影响喷射器性能的一个重要因素。面积比,如式(7)所示,为恒面积段截面积与喷嘴喉部截面积的比值。

式中:dm为恒面积段截面的直径,mm;dnozz为喷嘴喉部截面的直径,mm。
S.Varga 等[45]采用可变喉部面积喷射器,在保持恒面积段直径不变的情况下,通过改变喷嘴直径,控制面积比在13~27 范围内,利用CFD 研究了面积比对喷射系数的影响。结果表明,在恒定的工作流体压力和引射流体压力条件下,虽然喷射系数随面积比的增加而增加,但这也导致了临界背压变小。因此,面积比存在一个最佳值,应根据工况条件选择其值。当面积比取21 时,喷射系数取到最大值0.26,这与Sun Dawen[46]在类似工况下的结果吻合度较高。S.Varga等[47]还通过实验将结果与CFD 数据进行了总结和比较,发现CFD 与实验的工作流体流量吻合较好,平均相对误差为7.7%,但CFD 对引射流体流量及引射系数的预测平均相对误差约20%。Pei Pucheng等[48]利用CFD 对燃料电池用喷射器的结构进行了优化研究,该喷射器利用高压一次氢气引射未反应完全的二次氢气,最佳面积比范围为9~12.53。Ma Xiaoli 等[49]提出了在喷嘴喉部内实现可移动主轴的方法,使喷嘴喉部面积在操作者的控制下动态变化,当主轴远离喷嘴时,喷嘴喉部面积增加,从而改变面积比。研究发现,当主轴位置向喷嘴方向移动时,由于一次流量的减少,引射流量减少,存在最佳喷射系数。临界背压随主轴尖端到喷嘴距离增加而显著增加。V.V.Nguyen 等[50]通过移动主轴、改变喷嘴出口位置,从而调节面积比,发现与固定结构喷射器相比,可变几何结构喷射器的性能得到较大提高。
对于恒面积段长度,K.Pianthong 等[51]认为,随着恒面积段长度的增加,临界背压缓慢增加,达到一定极限后开始下降。但是最大喷射系数几乎不受恒面积段长度的影响。Yan Jia 等[52]数值模拟的结果也显示恒面积段长度对喷射系数的影响很小。Chen Weixiong 等[15]的数值模拟结果显示,随着恒面积段长度与直径之比从2 增至10,当引射压力较低时,喷射系数先增大而后趋于稳定;当引射压力较高时,该长径比对喷射系数的影响不大。
3.4 扩压段
扩压段的结构尺寸包括扩压段长度、发散角。K.Banasiak 等[53]研究了扩压段发散角对喷射器对功恢复效率的影响,数值模拟结果显示,最佳发散角约3°。当发散角由2°减至1°时,扩压段内壁的摩擦效应加剧使得该效率迅速降低,而当发散角由3.5°增至15°时,动量混合的不完全导致该效率缓慢降低。Li Shengyu 等[54]利用CFD 研究了扩压段长度对喷射系数的影响,喷射系数随着扩压段长度的增加先迅速增加再缓慢减小。M.S.Lee 等[55]也借助CFD 对喷射器扩压段尺寸进行了优化。Yan Jia 等[56]的数值模拟结果显示,在其所研究的范围内,扩压段长度对喷射系数的影响很小。Dong Jingming 等[57]的CFD模拟结果表明,在相同的恒面积段长度下,其所研究的几种扩压段长度对应的喷射系数几乎一致,而临界背压随扩压段长度的增加而增大并趋向于某一恒定值。
4 喷射制冷技术的应用
喷射制冷技术的应用形式主要是各类喷射制冷系统,包括单级喷射制冷系统、多级喷射式制冷系统、喷射-压缩复合制冷系统、喷射-吸收复合制冷系统、无泵喷射制冷系统等[58-59]。
喷射制冷系统的性能系数COP 被定义为制冷循环获得的制冷量与输入系统的能量之比,即:

式中:Qe为系统制冷量,kW;Qg为发生器热,kW;Wpump为循环泵功,kW。
由于发生器热与泵功在能量品位上差别较大,用上述指标衡量系统的优劣是有欠缺的。可以采用系统效率来评价热和机械能共同驱动的系统在热力学理论研究方面似乎更为合理,但如上文所述,概念本身存在的问题,使得这一评价指标在很多场合会失去实际意义。热和机械能共同驱动的系统性能评价本文不做讨论。
4.1 单级与多级喷射制冷系统
单级喷射制冷系统是形式最简单的喷射制冷系统,原理如图6所示。发生器出口的高温高压制冷剂气体作为工作流体经喷射器喷嘴加速,在接受室中引射来自蒸发器的低压制冷剂,二者在混合室中完成动量交换、质量交换后经扩压室排入冷凝器。冷凝器出口的制冷剂分为两股,一股经循环泵加压送入发生器,另一股经节流阀降温降压后送入蒸发器。在喷射制冷系统中,喷射器在临界条件下运行,为系统提供稳定的喷射系数、制冷量和COP,当背压超过临界背压,喷射器性能将显著降低。

图6 单级喷射制冷系统Fig.6 Single stage ejector refrigeration system(SERS)
考虑到工况条件的影响,Z.Aidoun 等[60]基于热力学模型对单级喷射制冷系统进行了模拟,研究了设计工况和非设计工况下的喷射器性能。研究发现在非设计工况下,由于混合不充分和激波的存在,增加了内部过热的产生。为了防止内部凝结,喷射器进口需要设置大约5 ℃过热度,但过大的过热度会限制冷凝器的效率。B.Gil 等[61]在蒸发温度10 ℃、冷凝温度40 ℃、发生温度70~200 ℃的工况下,通过数值手段研究了不同工质(丙酮、苯、环戊烷、环己烷、甲苯、R236ea、R236fa、R245ca、R245fa、R365mfc、RC318)在喷射制冷循环中的性能,结果表明每种工质的最佳喷射系数、最大COP 以及对应的最佳发生温度均不相同。
有学者将预热器、预冷器引入单级喷射制冷系统[62],原理如图7所示。预热器与预冷器的本质均为回热器,但它们布置的位置及目的有所差异。预热器被设置在喷射器出口与发生器入口,即喷射器出口的制冷剂加热即将进入发生器的制冷剂,降低了发生器所需的加热量,减小了冷凝器的负荷。预冷器被设置在冷凝器出口与蒸发器出口,即用蒸发器出口的制冷剂冷却冷凝器出口即将进入蒸发器的制冷剂,降低了冷凝器的负荷,保证了进入喷射器制冷剂的过热度,但降低了系统制冷量。Sun Dawen 等[63]对该系统进行了理论研究。研究发现,如果在循环中引入预热器,则可减少热输入量和冷却负荷,在所研究的工况下COP 可提高约20%。但额外的两个换热器,导致额外的成本且增加了系统复杂程度。引入预热器可以提高系统COP,虽然设置预冷器不一定能提高系统COP,但有时可以降低系统能耗,预冷器的设置有没有意义取决于蒸发器出口制冷剂为预冷器提供的冷量是否多余。例如,在压缩空气冷冻干燥技术中,为确保压缩空气中的含湿量达到要求,需将其降温至压力露点2~10 ℃,而用气设备并不需要如此低的温度,往往在蒸发器前设置一个预冷器,用蒸发器出口的低温压缩空气预冷蒸发器前的高温压缩空气,可以回收多余的冷量,从而降低了蒸发器的负荷。
基于单级喷射制冷系统,有学者提出了一种朗肯-喷射制冷复合系统,最典型的循环原理如图8所示。该类系统利用汽轮机等透平机械的乏汽作为工作流体驱动喷射器,在获得输出电功率的同时产生制冷量,即冷电联产。Zheng Bin 等[64]对该系统进行了理论研究,喷射器由汽轮机的乏汽驱动,系统可同时产生电力和制冷量。以R245fa 为工质,在tg=122℃、tc=25 ℃、te=70 ℃的工况下,效率为56.8%,且大部分损失发生在喷射器中。A.Habibzadeh等[65]理论研究了不同工质(R123、R141b、R245fa、R600a、R601a)对该种系统性能的影响,结果表明,R141b 对应的的最佳压力最低,R601a 对应的的损失最低。P.Haghparast 等[66]研究了喷射器几何形状对带有两级蒸发器的朗肯-喷射复合系统性能的影响,该系统可以提升传统有机朗肯循环的输出电功率。结果表明,输出电功率随喷射器面积比、引射流体流量的增加而提高,随喷嘴喉部直径、工作流体压力的增加而降低,随恒面积段直径的增加而提高。A.Ahmadzadeh 等[67]研究了一种由太阳能驱动的联合朗肯-喷射制冷系统(CPER),功率为50 kW。该系统主要由两个循环组成:集热器循环和制冷循环。通过热力学计算及分析,结果表明,热能利用率提高25.5%,效率提高21.27%,总成本降低7.76%。Zhang Chenghu 等[68]提出了一种同时输出功率和热量的新型有机朗肯循环与喷射式热泵相结合的系统。该系统仍以汽轮机乏汽作为工作流体驱动喷射器,与传统的有机朗肯循环相比,新型联合循环最大净输出功率提高10.78%,最大热回收能力提高19.04%。之后还对朗肯循环与喷射式热泵并联布置的系统进行了热力学分析[69]。也有学者对朗肯循环与喷射制冷循环相结合的冷热电联产系统进行了研究[70]。而在另一种与朗肯循环相结合的喷射制冷系统中[71],喷射制冷子系统相对独立,喷射器并不是由汽轮机的乏汽驱动,可视为两子系统的复合式系统。

图8 朗肯-喷射制冷复合系统Fig.8 Combined SERS and power system
太阳能作为可驱动喷射式制冷的低品位热源之一,近些年得到了学者们的广泛关注,其最初的形式如图9[72]。由于存在制冷剂泄漏风险以及太阳能子系统与喷射制冷子系统的耦合导致控制困难等原因,该系统的应用受到了限制。因此,该系统的另一种形式出现了,如图10所示。该系统中,太阳能子系统通过中间换热器将集热器收集的热量传输给喷射制冷子系统,以驱动后者运行。与传统的蒸气压缩制冷系统相比,此系统COP 更高,更环保。但由于太阳能间断、不连续,所提供的热量不稳定,使得该系统的整体效率较低。学者们研究了集热器[73-76]、太阳辐射强度[77]、蓄能装置[78-81]、可变几何形状喷射器[82-84]对该系统性能的影响。
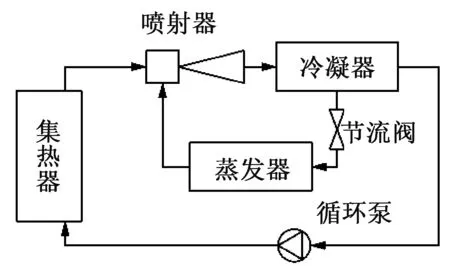
图9 太阳能喷射制冷系统Fig.9 Solar-driven ejector refrigeration system(SoERS)

图10 含中间换热器的太阳能喷射制冷系统Fig.10 Solar-driven ejector refrigeration system with intermediate heat exchanger
此外,有学者对该系统与朗肯循环的耦合系统进行了研究,原理见图11。M.Elakhdar 等[85]对该系统进行了动态模拟,集热器类型为抛物线槽式,他们研究了不同制冷剂(R601a、R245fa、R123、R141b)对喷射系数、系统COP 的影响,结果表明,R601a 提供的喷射系数和COP 最高。此外,有学者还研究了与之类似的太阳能驱动的冷热电三联供系统[86-87]。

图11 朗肯-太阳能喷射制冷系统Fig.11 Solar-driven ejector refrigeration system combined with a power cycle
含多个喷射器的喷射制冷系统、含多个蒸发器的喷射制冷系统等在一定情况下既能满足不同的系统需求,又能提高传统喷射制冷系统的性能。考虑到固定几何形状喷射器的变工况适应性较差,F.Aligolzadeh 等[88]提出了多种不同尺寸喷射器并联布置的系统形式,如图12所示,每个喷射器仅在特定的背压范围内工作,即背压决定喷射器运行的方案,该系统可以在工况变化的情况下以较高的效率连续运行。

图12 一种多喷射器制冷系统Fig.12 Multi-ejector refrigeration system
关于多级喷射制冷系统,Xing Meibo 等[89]提出使用两个喷射器从传统的两级蒸气压缩制冷系统中回收节流过程损失的功,系统COP 可提高10.5%~30.6%。Chen Guangming 等[90]提出了一种由两个热源驱动的两级喷射制冷系统,如图13所示,该系统可由两种不同品位的热源驱动,以R236fa 为工质对该系统进行了实验模拟。结果表明,在低于21.7 ℃的冷凝温度下,后一种系统的性能优于常规单级系统。

图13 一种由两个热源驱动的两级喷射制冷系统Fig.13 Two-stage ERS driven by two heat sources
4.2 喷射-压缩复合制冷系统
近年来,喷射-压缩复合制冷系统得到了广泛的研究。喷射器喷射系数与运行工况对喷射制冷系统性能的影响至关重要。对于单级喷射制冷循环而言,当其他参数不变,蒸发压力增大时,喷射系数以及冷凝压力也会增大。本文介绍三种类型的喷射-压缩复合系统,第一种类型可称为含压缩机的喷射制冷系统,其中压缩机的作用主要是提升引射流体的压力;第二种类型可称为含喷射器的蒸气压缩制冷系统,其中喷射器主要是作为一种膨胀装置;第三种类型,喷射-压缩复叠系统,该类系统由喷射子循环与压缩子循环组成。
第一类系统于1990年由M.Sokolov 等[91]提出,其基本形式如图14所示,在传统单级喷射制冷系统的基础上引入压缩机,置于蒸发器出口,增加引射流体的压力,从而提高了喷射器的性能。Xu Yingjie等[92]对传统的含压缩机的喷射制冷系统进行了改进,即在蒸发器入口增加了气液分离器和节流阀,如图15所示。结果显示,在所研究的工况下,新系统COP 可达6.30,较前者提高了21.95%,表明新系统具有更好的节能潜力。杨悦等[93]对以太阳能为热源的此类系统进行了热力学分析,研究了压缩机压比对系统性能的影响,结果表明存在最佳压比为1.45。

图14 含压缩机的喷射制冷系统Fig.14 ERS with a booster compressor

图15 一种改进的含压缩机的喷射制冷系统Fig.15 Improved ERS with a booster compressor
针对第二类含喷射器的蒸气压缩制冷系统,其原理如图16[94],将喷射器并入蒸气压缩循环一方面可减少与膨胀装置相关的不可逆损失,另一方面提高了压缩机吸入压力,减小了压缩功,从而提高COP。

图16 含喷射器的蒸气压缩制冷系统Fig.16 Compression refrigerating system with an ejector
E.Nehdi 等[94]研究了蒸发温度、冷凝温度、喷射器面积比、工质对该系统COP 的影响,采用R141b 时系统性能较好,最大COP 为4.9。当以R141b 为工质,tc=30 ℃,te=-15 ℃,面积比取最佳面积比时,该循环COP 较传统压缩式循环提升约22%。H.K.Ersoy 等[95]以R124a 为工质对该系统进行了实验研究,COP 比传统压缩系统高6.2%~14.5%。N.B.Sag 等[96]以R134a 为工质进行了实验研究,与传统系统相比,COP 增加了7.34%~12.87%,效率增加了6.6% ~11.24%。Wang Xiao 等[97]从理论上对4种不同的含喷射器的蒸气压缩制冷系统进行了比较。还提出了一种新的循环,将喷射器置于蒸发器和气液分离器之间,使其具有更好的性能。也有学者提出了其他配置形式[98-99]。
D.A.Dokandari 等[100]对该系统的复叠式系统进行了研究,即将高温循环的蒸发器作为低温循环的冷凝器,分别以CO2和NH3作为低温循环和高温循环的工质。与传统的蒸气压缩式复叠系统相比,该系统的COP 和第二定律效率较前者分别提升7%和5%。
M.Elakdhar 等[101]提出了一种在不同压力水平下运行的双蒸发器系统。如图17所示,在该系统中,喷射器将从两个蒸发器出口的工质进行混合,与常规循环相比,该循环使COP 提高了32%。由于与传统的蒸气压缩制冷相比,喷射器提高了压缩机进口的工质压力,故压缩机仅需要很少的功率输入。

图17 一种含多个蒸发器的喷射-压缩复合系统Fig.17 Multi-evaporator ERS
此外,T.Rostamnejad 等[102]对第一类与第二类相结合的复合系统进行了研究,如图18所示,以效率为目标函数对该系统的工质进行了筛选,并与第二类含喷射器的蒸气压缩制冷系统和常规蒸气压缩制冷系统进行了比较。结果表明:在所研究的6 种工质中,R1234ze 最为理想,在冷凝温度为40 ℃和蒸发温度为5 ℃时,该系统的效率分别比后两者高5.7%和15.5%。

图18 含额外压缩机及喷射器的压缩制冷系统Fig.18 Compression refrigerating system with an extra ejector and compressor
第三类是喷射-压缩复叠系统,该类循环由喷射子循环与压缩子循环组成。1993年,M.Sokolov等[103]首先提出了这种系统,原理如图19所示。太阳能喷射子系统与压缩子系统间设一接触式换热器作为中间冷却器,该换热器既作为太阳能喷射子系统的蒸发器,也作为压缩子系统的冷凝器。A.Arbel等[104]对该系统进行了理论研究,证明了其可行性。Sun Dawen[105]将文献[103]采用的中间接触式换热器换成了间壁式换热器,并对该系统进行了数值研究,并分别以R134a、水作为压缩子循环、喷射子循环的工质,结果表明,该联合循环系统COP 比常规循环增加50%。H.Vidal 等[106]利用TRNSYS 对带有蓄热器的该系统进行了动态模拟,分别以R141b 和R134a作为喷射子循环和压缩子循环的工质,对中间换热温度以及平板集热器面积进行了优化。K.Megdouli等[107]对喷射子循环与两个压缩子循环三者复叠的系统进行了研究,将喷射制冷系统作为第三级冷却循环,从高温冷凝器回收余热。在总损失最小化的情况下,通过理论证明了该系统与两个压缩子循环复叠的系统相比具有更高的COP 和更低的损失。Chen Guangming 等[108]提出了一种提高喷射-压缩复叠系统效率的方法,即利用压缩子循环压缩机出口的过热CO2蒸气预热喷射子循环发生器前的制冷剂,从而提高整个系统的效率。分别以R245ca、R600、R601b 为喷射子循环工质对蒸发温度-40~0 ℃范围内的系统性能进行了分析。研究结果表明,该方法在低蒸发温度下对提升系统性能更有效。乔夏莹等[109]对图19所示系统进行了热力学分析,研究了发生温度、中间温度、冷凝温度和蒸发温度对系统性能的影响。
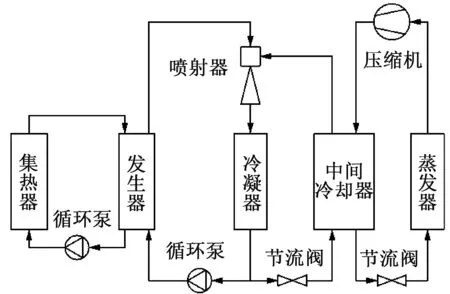
图19 一种太阳能喷射与压缩结合的制冷系统Fig.19 Combined SoERS with compression refrigeration system
4.3 喷射-吸收复合制冷系统
吸收式制冷是常见的制冷方式之一,最基本的形式如图20,原理及分类可以参考文献[110]。吸收式制冷可由各种低品位热源驱动,但是与传统的蒸气压缩制冷相比,其系统COP 普遍较低。

图20 吸收式制冷系统Fig.20 Absorption refrigeration system
喷射-吸收复合制冷循环最早由Chen Liting[111]提出,在这种循环中,喷射器引射蒸发器中的制冷剂至吸收器,原理如图21所示。系统高度依赖于喷射器几何形状,最佳COP =0.85,而常规循环在相同工况下(tg=120 ℃、tc=40 ℃、te=5 ℃)的COP =0.68,当冷凝器温度降低至30 ℃,COP 可达1.5。C.Vareda 等[112]数值模拟了喷射器混合段直径对该系统性能的影响。该系统以氨-硝酸锂为工质对,喷射器位于吸收器入口,取代溶液膨胀阀。液-气喷射器从蒸发器中吸入制冷剂蒸气,吸收器压力高于蒸发器压力,而不需要额外的能源消耗。结果显示:与传统的单效吸收式制冷循环相比,喷射器的设置使得发生温度降低约9 ℃,且在中等温度范围COP 升高;其次,混合段的直径对系统COP 影响较大,可变几何形状的喷射器更有利于系统控制与优化。Liang Xiao等[113]提出一种采用两个喷射器的吸收式制冷系统,即设置额外的喷射器替代图21所示系统中的循环泵,该喷射器由发生器出口的高压工质驱动。热力学分析结果表明,与传统的吸收式制冷系统相比,尽管该系统无需循环泵,但由于牺牲了部分制冷剂流量,使得系统COP 降低。

图21 喷射-吸收复合制冷系统(a)Fig.21 Combined ejector-absorption refrigeration system(a)
另一种喷射-吸收复合制冷系统的原理如图22所示[114],将喷射器置于发生器和冷凝器之间,增加了蒸发器中制冷剂的流量,从而实现性能的提升。作者研究了运行工况参数对该系统喷射系数、COP 的影响,在tc=30 ℃,te=5 ℃或te=10 ℃的条件下,该系统最佳COP 较传统单效吸收式制冷系统高20%~40%。

图22 喷射-吸收复合制冷系统(b)Fig.22 Combined ejector-absorption refrigeration system(b)
G.K.Alexis 等[115]从理论上对这两种系统进行了比较,在相同的发生温度、蒸发温度条件下,第二种系统(引射蒸发器中的工质排至冷凝器)提供的COP介于1.099~1.355 ,高于第一种系统(引射蒸发器中的工质排至吸收器)的COP,介于0.274~0.382 。
Hong Daliang 等[116]提出了一种改进的喷射-吸收复合系统,该系统在高热源温度下为双效循环,在低热源温度下为单效循环。低压发生器出口处的部分制冷剂蒸气被高压发生器出口处的制冷剂蒸气直接引射至冷凝器,通过使用喷射器,降低了外部热源的品位,系统COP 比传统的单效循环高30%。Yan Xiaona 等[117]对文献[16]提出的系统进行了实验研究。结果表明,系统COP 比单效吸收式制冷系统高30%,发生温度比双效吸收式制冷系统至少低20 ℃,实验结果与理论结果吻合度较高。
Shi Yuqi 等[118]提出了一种双热源驱动的喷射-吸收复合制冷系统并进行了实验研究,该系统借助喷射器,以高压发生器中蒸气为工作流体,引射低压发生器出口的蒸气。在该系统中,从低压发生器引出的蒸气流量多于传统的双效循环,这意味着可以使用更多的低品位热量,系统所需的输入热量和驱动循环所需的热源温度可以降低。该研究以溴化锂-水作为工质对,185~215 ℃的热空气作为高温热源,太阳能集热器加热的热水作为低温热源。在热空气进口温度215 ℃的工况下,该系统的COP 可达0.95,比单效循环高约20%,且驱动温度比传统的双效循环低。此外,喷射-吸收复合系统也可以与有机朗肯循环相结合。Wang Jiangfeng 等[119]对一种与朗肯循环相结合的喷射-吸收复合系统进行了研究,该系统可同时输出功率(612.12 kW)和制冷量(245.97 kW)。作者研究了各工况参数(即发生温度、冷凝温度和蒸发温度、汽轮机进出口压力、溶液氨浓度)对系统性能(即制冷量、净输出功率和效率)的影响,结果表明,喷射器的引入提高了传统系统的性能。K.Abdul等[120]对太阳能驱动的结合了朗肯循环的第二种喷射-吸收复合系统进行了分析,结果显示,太阳能集热器的损失最大,太阳能子系统以R141b 为工质时,其损失占总损失的79.61%。
4.4 无泵喷射制冷系统
在喷射制冷系统中,尽管泵的功率远小于其他部件,耗电量较小,但它往往是系统中唯一的运动部件,需要更多的维护成本,并且在运行过程中,泵与其他部件相比更可能出现故障。此外,对于废热驱动的喷射制冷系统,泵是唯一用电设备,如果采用无泵喷射,不仅可省去高品位电能的消耗,而且系统可应用于无电力场所。因此,无泵喷射制冷系统被广泛的研究。总的来说,该类系统有如下几种:重力式、旋转式、热驱动式以及热管-喷射制冷系统。
重力式无泵喷射系统的基本配置如图23所示。V.M.Nguyen 等[121]提出了一种重力式无泵喷射循环,以水为工质搭建了一台制冷量7 kW 的样机。由于发生压力、冷凝压力、蒸发压力依次降低,故要使工质在无泵的情况下完成循环,发生器、冷凝器、蒸发器需从高到低布置,换热器之间的压差通过它们之间的高差补偿,该系统高度约7.5 m。J.Kasperski[122]指出,系统布置的高差主要由工质种类和工况决定。该类系统的主要缺点是高差限制导致的对场地的高度要求,以及管道长度较长引发的阻力大、热耗散大的问题。J.Kasperski[123]还提出过一种旋转式的无泵喷射系统,该系统利用离心力克服压差,可缩小重力式系统的尺寸和工质的充注量。

图23 重力式无泵喷射系统Fig.23 Gravity pumped ejector system
针对热驱动式无泵喷射系统,Huang B.J.等[124]提出过一种多功能发生器的喷射制冷系统,其原理如图24所示。该系统包括两个发生器,由一个蒸气发生器和一个排气室组成。蒸气发生器加热工质升高压力,而排气室冷却工质降低压力,两个发生器通过阀切换交替运行,以此产生压差驱动工质循环。实验结果表明:在tg=90 ℃、tc=32.4 ℃、te=8.2 ℃的工况下,COP 为0.22。

图24 一种热驱动式无泵喷射系统Fig.24 Ejector system with thermal pumping effect
S.B.Riffat 等[125]提出了一种热管-喷射制冷系统,基本原理如图25所示。该系统由热管、喷射器、蒸发器和节流阀组成。发生器中的工质被加热升压,在喷嘴中加速从而引射蒸发器中的低压工质,二者混合后进入冷凝器,冷凝器中的一部分工质经节流阀后进入蒸发器,另一部分通过热管内壁材料的毛细作用返回发生器完成循环。以甲醇、乙醇和水为工质对该系统进行了理论研究,结果显示,甲醇的效果较好,系统COP 可达0.7。B.M.Ziapour 等[126]对前人提出的这种系统进行了能量和分析。计算结果表明,系统COP、第二定律效率均随着蒸发温度的升高和冷凝温度的降低而增大。总损失随着冷凝温度、发生温度的升高而增大,随蒸发器温度的升高而降低。对于大直径热管,在tg=100 ℃、tc=30 ℃、te=10 ℃的工况下,COP 可以达到0.30。此外,Ling Z.[127]还提出一种垂直布置的基于虹吸效应的热管-喷射制冷系统。

图25 热管-喷射制冷系统Fig.25 Combined heat pipe and ejector refrigeration system
5 总结与展望
本文首先对喷射器的工作机理以及喷射系数、压缩比、膨胀比和喷射器效率等常见的评价指标进行了介绍。其次,回顾了喷射器设计理论模型的发展历程,阐述了喷射器喷嘴、接受室、恒面积段和扩压段尺寸对其性能的影响。最后,对主要的几种喷射制冷系统展开了讨论,即单级与多级喷射制冷系统、喷射-压缩复合制冷系统、喷射-吸收复合制冷系统、无泵喷射制冷系统。
喷射器模型的研究方面,大多基于理想气体、绝热边界、入口速度为零、径向温度与速度均匀分布等假设,或采用将斜激波近似为正激波、引入等熵效率系数等简化手段。这些假设或简化手段是模型准确性不足的重要原因。
结构尺寸对喷射器性能的影响研究方面,大量研究证明,喷嘴出口位置、喷嘴收敛角、发散角、接受室收敛角、恒压混合段长度、面积比、扩压段长度均存在最佳值,而恒面积段长度在一定范围内并不会显著影响喷射器性能,各参数变化对喷射器性能影响的剧烈程度各不相同。
喷射制冷技术方面,近年来学者们进行了大量的应用研究。对于工质的选择,不同工质适用的最佳工况温度范围不同,应根据实际工况合理选择工质,以保证系统安全、高效的运行。对于单级喷射制冷系统,预热器的引入可以提高系统COP,但预冷器未必,设置预热器、预冷器的必要性应根据其中热量、冷量的来源以及技术经济分析综合考虑。对于喷射-压缩复合制冷系统,这两种子系统的复合既可以降低传统压缩系统的能耗,也可以提升传统喷射系统的性能。喷射制冷与吸收式制冷均为低品位热源可驱动的系统,二者的结合使得系统性能得到了很大的改善。无泵喷射制冷可用于无电力环境,这一优势是其他系统难以替代的。
由于篇幅限制,本文没有介绍喷射器内部流动及能量传递的数值模拟以及可视化研究,也没有介绍不同工质在喷射制冷系统中的应用特性研究。
从本文讨论可以看出,喷射器由于结构简单,可靠性高,可利用低品位热能作驱动力,近年来引起学界以及工业界的广泛关注。但是,能源效率不高、环境适应性不强,仍然是喷射器得到大规模应用的重要障碍。因此,建议进一步开展下列研究工作:
1)从热力学机理着手,研究喷射器可能达到的理想最高效率,以此作为喷射器性能完善度的衡量指标;
2)深入开展喷射器内部流动、能量交换、动量交换等机理的研究,特别是有关超声流动激波产生、激波强度、激波消除等机理的研究以及超声两相流动机理研究。在此基础上,优化设计沿流动方向喷射器内表面型线,以减少喷射器内部的不可逆损失;
3)深入研究外部工况参数与喷射器内部几何参数之间的关系,研究内部几何参数可调的喷射器结构,提高喷射器对外部工况变化的适应性;
4)开展喷射器应用技术研究,包括针对不同应用场合开展不同流程以及相应工质选择的研究,以提高整个系统的能源利用率。

