“整数梯度下降”算法对热泵用翅片管蒸发器流路的优化

张浩 侯泽飞 李杏党 樊超超 晏刚 褚雯霄 王秋旺

(1 广东美的制冷设备有限公司 佛山 528311；2 西安交通大学能源与动力工程学院 西安 710049)

翅片管换热器广泛应用于制冷空调领域，其性能直接影响整机系统的制冷(热)量和能效(COP)。目前关于翅片管换热器的优化主要集中在翅片间距、翅片类型、管间距、管径、制冷剂流路等方面[1－3]。其中，换热器制冷剂流路优化无需增加额外部件，不改变原有换热器结构，是一种有效提升系统性能的方式[4－5]。

换热器制冷剂流路优化可采用实验和仿真两种方法。仿真方法具有工作量小、优化周期短等优势得到广泛应用。换热器仿真模型多采用分布参数法构建，将换热器分为过冷区、两相区和过热区，对每个区域均进行微元控制体划分和计算[6－7]。利用仿真模型可得到换热器的换热特性及压降特性。对于提升换热器综合性能而言，传热系数越大越好、流体压降越小越好；但这两个因素往往相互制约、相互影响，因此难以用单一参数(传热系数或压降)来评价换热器综合性能。针对该问题，部分学者探究了基于热力学第二定律的换热器性能综合评价方法(熵产或损)。A.Cavallini 等[8]利用冷凝器制冷剂侧熵产来评价冷凝器综合性能，并深入探讨了冷凝器流路对制冷剂侧熵产的影响。W.J.Lee 等[9]提出了一种基于热力学第二定律的冷凝器分路数优化方法。研究表明:目前关于制冷剂流路优化的研究主要是针对单独的换热器部件尤其是冷凝器，而在系统层面上进行蒸发器流路优化的研究较少。根据ISO 5151 标准[10]，在测试热泵型房间空调器性能时，需调整压缩机运行频率使得系统制热量与额定值相同。因此针对热泵用翅片管蒸发器，在对比不同制冷剂流路性能的同时，本文设定制冷剂入口焓值和蒸发器出口过热度，通过迭代求解制冷剂质量流量保证不同流路蒸发器换热量相同，再通过熵产进行不同流路蒸发器性能比较。本文还对比了实验结果与仿真结果，验证了蒸发器熵产仿真值与系统COP 实验值之间的对应关系，即蒸发器熵产的变化可用于预测热泵系统COP 的变化；利用上述仿真模型计算得出的蒸发器熵产可用来评价蒸发器综合性能。

构建蒸发器仿真模型并选择合适的综合性能评价参数后，需选择有效的优化算法来构建相应蒸发器流路优化模型。目前，有很多相关算法被应用到工程仿真中，如机器学习，遗传算法，梯度下降算法等[11－13]。梯度下降算法具有易实现，计算效率高等优势；由于蒸发器分路数为整数，因此本文采用“整数梯度下降”算法构建了热泵用蒸发器制冷剂流路优化模型，并获得了设计换热量为2 000～6 000 W 所对应的最佳蒸发器流路。

1 仿真模型

本研究选用熵产作为蒸发器综合性能的评价参数。对于翅片管蒸发器，熵产由制冷剂与空气之间的换热温差及流体压降产生；蒸发器熵产的增加会导致系统压缩机及风机功耗增加，从而降低系统性能。因此在进行蒸发器流路优化时，应尽量使蒸发器熵产最小。本文采用分布参数法构建仿真模型，利用Fortran 语言编写，选用R32 为制冷剂；模型中制冷剂的状态参数由NIST 制冷剂物性数据库得到[14]。

1.1 计算流程

为简化模型、提高计算效率，提出以下假设[15]:1)仿真模型中换热及流动过程均为稳态过程；2)U型连接管、分液器及其他连接管路处的热损失忽略不计；3)流经分液器的制冷剂被均匀分配。基于上述假设及能量守恒原则，使用以下公式进行蒸发器仿真模型建立:

其中，总传热系数k可表示为:

蒸发器制冷剂侧和空气侧的传热系数及压降根据表1所示的经验关联式进行计算。

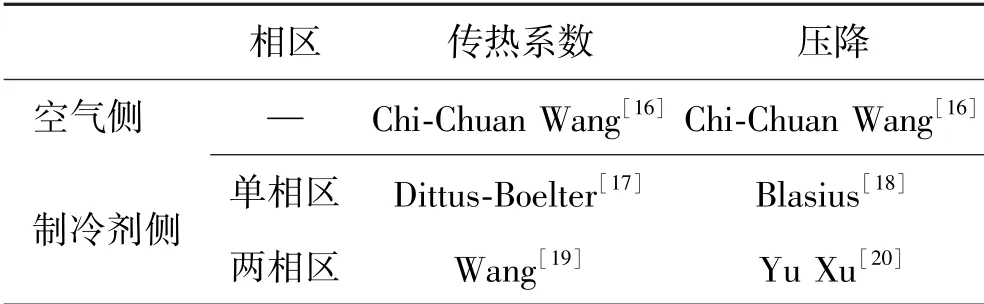
表1 传热系数及压降关联式Tab.1 Heat transfer and pressure drop correlations

析湿系数ξ和翅片效率ηa的计算如下[21]:

蒸发器U 型连接管处的制冷剂压降δpr.b由下式计算[22]:

基于上述经验关联式，建立气体旁通蒸发器的仿真模型，蒸发器的熵产通过下式进行计算[23]:

仿真模型的求解过程如图1所示，蒸发器制冷剂入口焓值由冷凝器出口制冷剂状态决定(等焓节流过程)，通过计算换热面积与实际换热面积的比较迭代求解蒸发器制冷剂入口压力；通过计算换热量与设计换热量的比较迭代求解制冷剂质量流量。采用上述仿真模型即可得到不同制冷剂流路的熵产、制冷剂进口压力、制冷剂压降的参数。

图1 仿真模型求解过程Fig.1 Calculation procedure of the simulation model

1.2 蒸发器流路及结构参数

蒸发器结构参数如表2所示，蒸发器流路如图2所示。制冷剂分2 路(分路数I)进入蒸发器，流经前半段蒸发器换热后汇合并经由分液器分为4 路(分路数II)进入后半段蒸发器。因此一个常规蒸发器的流路可由3 个参数确定，即前半段蒸发器分路数(NP-I)、分液器相对位置(RL)和后半段蒸发器分路数(NP-II)；其中分液器相对位置(RL)定义为前半段蒸发器管数与蒸发器总管数之比。本文将蒸发器流路标记为“NP-I-RL-NP-II”，例如:图2所示流路被标记为“2-0.2-4”。RL＝0 即制冷剂在进入蒸发器前已被分成若干路。

表2 蒸发器结构参数Tab.2 Geometric parameters of the evaporator

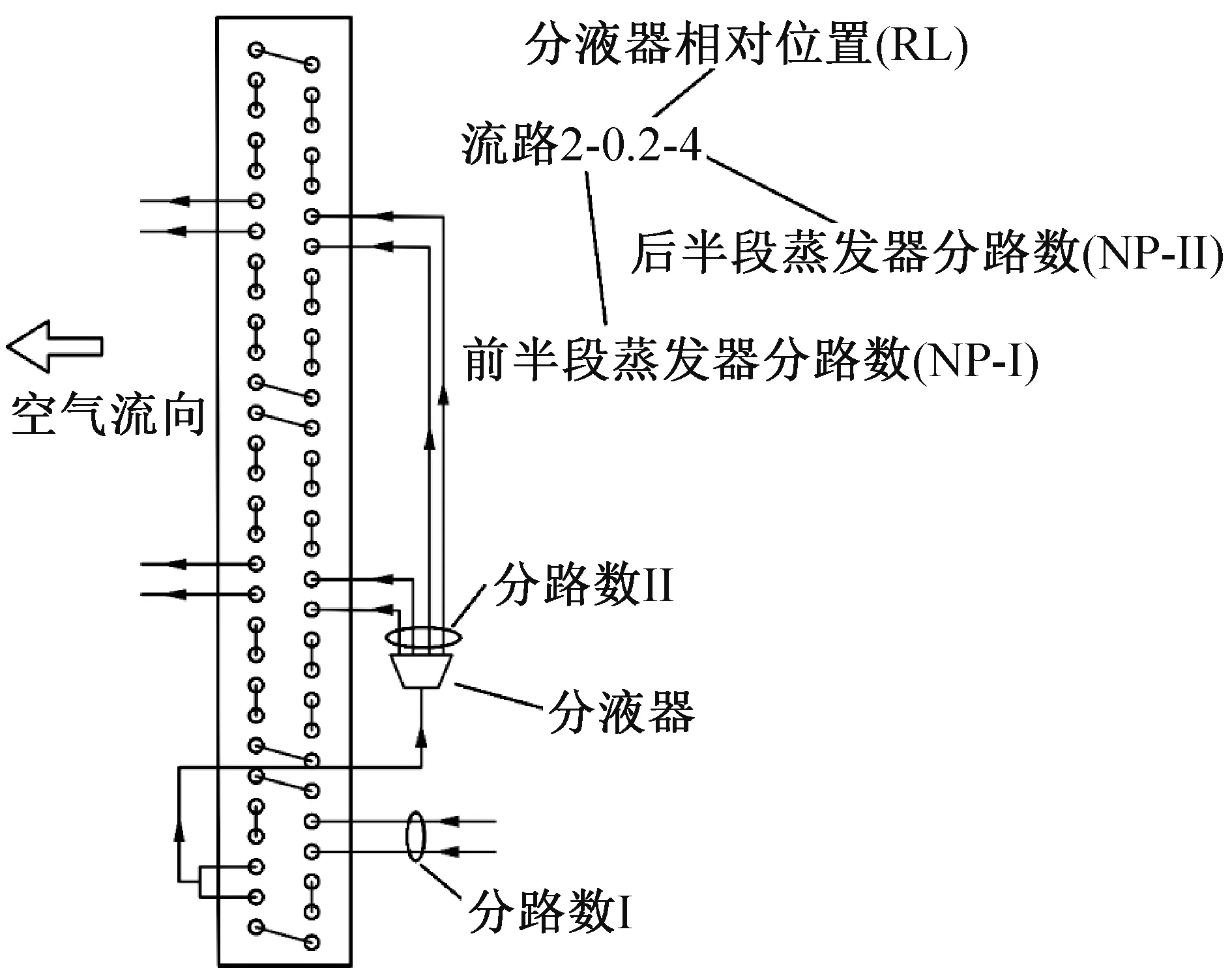
图2 蒸发器流路Fig.2 The evaporator refrigerant circuit

当蒸发器分路数减少或分液器相对位置后移时，蒸发器管内制冷剂平均流速增大，管内表面传热系数增大，制冷剂侧压降增大。管内表面传热系数增大有利于系统性能提升，而制冷剂侧压降增大不利于系统性能提升，此外制冷剂侧压降会直接影响平均蒸发温度和换热温差。综上所述，蒸发器流路对于蒸发器综合性能的影响非常复杂，难以用单一传热或压降参数来评价其综合性能；基于热力学第二定律的熵产可以反映传热系数和压降之间的平衡关系，以下将详细探究蒸发器流路对其熵产的影响。

2 仿真结果及分析

蒸发器流路可用3 个参数表示，但在分析蒸发器流路对蒸发器熵产影响时，可将3 个参数简化为两个参数，即将前半段蒸发器分路数(NP-I)设置为1，仅研究分液器相对位置(RL)和后半段蒸发器分路数(NP-II)对蒸发器熵产的影响。如图3所示为20 种流路在不同设计换热量工况下的熵产变化情况。不同设计换热量工况下仿真模型的输入参数如表3所示。

图3 20 种蒸发器流路Fig.3 The twenty specific refrigerant circuits

表3 仿真模型的输入参数Tab.3 The input parameters for simulation procedure

图4所示为3 种换热量工况下，制冷剂流路对蒸发器熵产的影响。在设计换热量1 000 W 工况下，当后半段蒸发器分路数(NP-II)为2、3、4 时，蒸发器熵产随分液器相对位置(RL)的增加呈先减小后增大的趋势。主要原因为其前半段蒸发器分路数(NP-I)为1，后半段蒸发器分路数(NP-II)为2～6，即前半段蒸发器管内制冷剂流速较大；当分液器相对位置(RL)后移时，前半段蒸发器在整个蒸发器中的占比增加，导致整个蒸发器的管内制冷剂平均流速增加，管内扰动增强，管内表面传热系数增大，而平均流速的增加会导致管内表面摩擦加剧，制冷剂侧压降增大；因此，在管内表面传热系数和制冷剂侧压降的双重作用下，对于NP-II 为2、3、4 工况均存在一个最佳RL 使得蒸发器熵产最小。此外，当NP-II 为6 时，管内制冷剂流速过低，导致管内表面传热系数成为了限制蒸发器综合性能的主要因素，此时增大RL 有利于提升管内制冷剂流速；因此在设计换热量1 000 W 工况，NP-II为6 时，蒸发器熵产随RL 增加呈下降趋势。

如图4(b)所示，当NP-II 为2 时，蒸发器熵产随RL 的增加而增大。因为在设计换热量2 000 W 工况下，制冷剂质量流量相较于1 000 W 工况较高，当NP-II 为2 时，管内制冷剂质量流速较高，此时制冷剂侧压降较高，导致蒸发器熵产增加，此时减小RL 有利于降低蒸发器熵产。NP-II 为3、4、6 时，蒸发器熵产随RL 增加呈先减小后增大趋势。

图4(c)所示为设计换热量3 000 W 工况下制冷剂流路对蒸发器熵产的影响。不同NP-II 条件下，制冷剂熵产均随RL 增加而增大。因为当设计换热量为3 000 W 时，蒸发器管内制冷剂流速较高，制冷剂与管内壁的摩擦加剧，此时制冷剂侧压降是限制蒸发器综合性能的主要因素；因此减少RL 或增大NP-II可以有效降低蒸发器熵产。综上所述，设计换热量1 000 W、2 000 W、3 000 W工况对应的最佳制冷剂流路分别为1-0.13-2、1-0.1-3、1-0-6。以上分析均基于仿真结果得出，为验证准确性，将对仿真结果与实验数据进行对比。

图4 流路对蒸发器熵产的影响Fig.4 Entropy generation variation of each refrigerant circuit

3 蒸发器熵产仿真值与系统COP 实验值之间的对应关系

验证仿真结果的实验在焓差实验室内进行，制热量测试偏差为±0.5%，COP 测试偏差为±0.75%。实验装置选用额定制热量为2 400 W 的变频热泵型房间空调器，空调器的室内换热器结构参数及相关配置如表4所示。根据ISO 5151 标准[10]，室内、室外的干湿球温度分别设置为20 ℃/15 ℃和7 ℃/6 ℃，为减小随机误差，针对每个工况条件均进行3 次测试，取3 次测试结果的算术平均值为最终结果。

表4 变频热泵型房间空调器相关参数Tab.4 Specifications of the tested inverter driven air conditioner

实验对5 种蒸发器流路进行了对比测试，分别为1-0.13-2、1-0.1-3、1-0.2-4、1-0.33-4、1-0-6，测试中通过调节压缩机运行频率使得系统制热量保持在1 200 W 和2 400 W，保证对不同流路蒸发器系统性能测试时，系统制热量相同。蒸发器熵产仿真值与系统COP 实验值之间的对比结果如图5所示。

图5所示为蒸发器熵产仿真值与系统COP 实验值的对比。对于两种制热量工况，熵产仿真值较小的蒸发器制冷剂流路所对应系统的COP 较高，即利用所述仿真模型计算得出的蒸发器熵产可用来预测相应实际热泵系统的COP 变化情况。由此，可见熵产仿真值最小化可以作为蒸发器流路优化的目标，以下将基于所述仿真模型，将蒸发器熵产选为“代价函数”，采用“整数梯度下降”算法构建蒸发器制冷剂流路优化模型。

4 热泵用蒸发器制冷剂流路优化模型构建

“整数梯度下降”是一种常用的优化算法，通过沿函数梯度方向反复搜索获得复杂函数的局部最小值[24－25]。NP-I、NP-II、RL 3 个蒸发器流路参数为优化参数，将3 个参数分别标记为θ1、θ2、θ3，则优化参数向量可表示为:

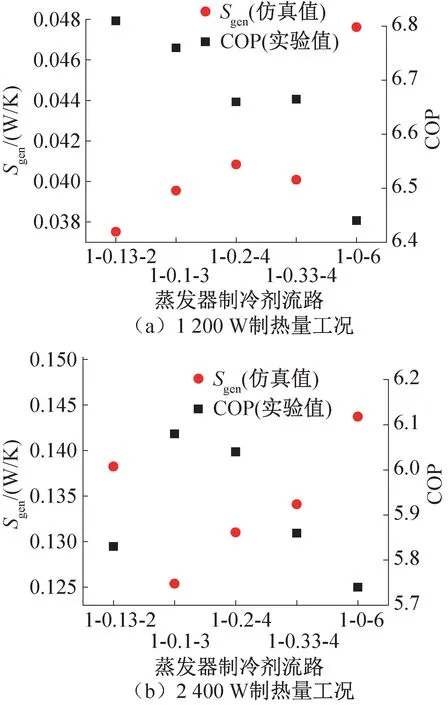
图5 蒸发器熵产仿真值与系统COP 实验值的对比Fig.5 The comparison between tested COP and theoretical entropy generation

选择蒸发器熵产作为“代价函数”，可表示为:

“代价函数”的梯度向量表示如下:

其中，“代价函数”在各个优化参数方向上的梯度由下式计算:

式中:梯度计算步长Δθ1、Δθ2、Δθ3分别为0.05、0.05、0.005。

“代价函数”的梯度向量即为优化参数向量的“下降方向”，具体优化方式如下式所示。

式中:β1、β2、β3分别为算法的下降步长，若下降步长过大，则函数最小值可能被跳过；而下降步长过小会影响计算效率。由于蒸发器的分路数为整数，故β1、β2分别设为相应梯度绝对值的倒数(如式(19)所示)；β3为0.1。为避免算法在求解过程中陷入局部最优点，在上一次求解完成后对初始优化参数向量θ0进行调整。本文在式(20)所示的向量空间内随机选取100 个初始优化向量θ0。

优化算法的计算流程如图6所示。

图6 优化算法求解流程Fig.6 Calculating procedure of the optimization algorithm

首先设定初始优化参数向量θ0，并利用蒸发器仿真模型计算熵产梯度向量∇Sgen，将优化参数向量沿梯度向量方向进行“下降”，若优化参数向量的变化值小于设定偏差ε，则记录优化结果，否则继续进行寻优；前一次求解过程完成后，调整初始优化参数向量并进行重复计算，直到100 个初始优化参数向量被完全检索。基于上述优化算法，求解出了设计换热量为2 000～6 000 W 所对应的最佳蒸发器流路，如表5所示。

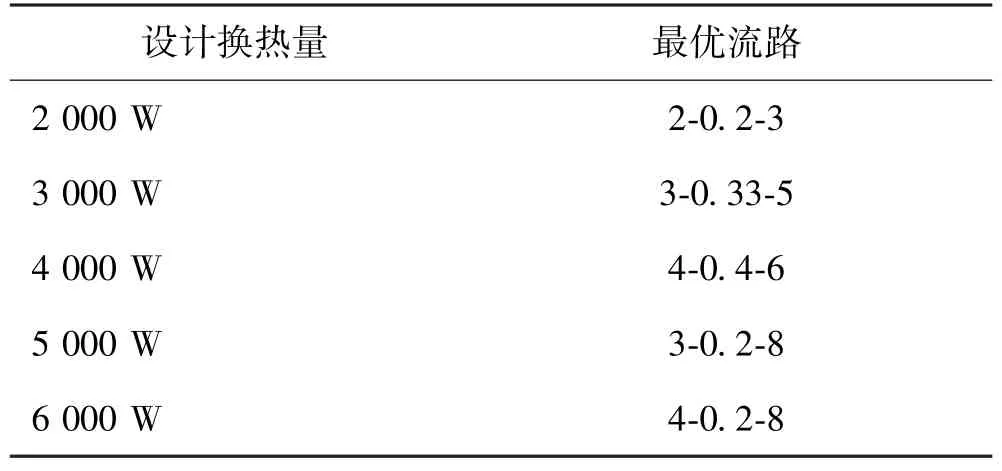
表5 设计换热量2 000～6 000 W 所对应最佳蒸发器流路Tab.5 The optimization results for various heat transfer capacity conditions

5 结论

本文采用分布参数法构建了热泵用翅片管蒸发器的仿真模型，研究了蒸发器制冷剂流路对蒸发器熵产的影响，并利用熵产最小化原理，提出了基于“整数梯度下降”算法的蒸发器流路优化方法。得到结论如下:

1)当蒸发器分路数减小或分液器相对位置后移时，管内制冷剂平均流速增加，管内表面传热系数和制冷剂压降增大；增大传热系数可提升蒸发器综合性能，但制冷剂压降增大会产生不利影响。熵产可对传热系数与压降进行综合考量，来评价蒸发器综合性能。仿真结果表明当蒸发器设计换热量增大时，最小蒸发器熵产所对应的分路数增加，且分液器相对位置前移。

2)通过对比实验与仿真结果，验证了蒸发器熵产仿真值与系统COP 实验值之间的对应关系，即蒸发器熵产(仿真值)的变化可用于预测热泵系统COP的变化。最小化蒸发器熵产(仿真值)可作为蒸发器流路的优化目标。

3)以熵产作为“代价函数”，采用“整数梯度下降算法”构建蒸发器流路优化模型，获得了设计换热量为2 000～6 000 W 所对应的最佳蒸发器流路。

符号说明

COP ——系统性能系数

q——控制容积的换热量，W

Q——蒸发器换热量，W

——质量流量，kg/s

h——比焓，kJ/kg

A——传热面积，m2

T——温度，K

k——总传热系数，W/(m2·K)

d——管直径，m

l——管长度，m

s——间距，m

tn——厚度，m

λ——导热系数，W/(m·K)

α——对流传热系数，W/(m2·K)

η——翅片效率

ξ——析湿系数

w——含湿量，g/(kg 干空气)

p——压力，kPa

ρ——密度，kg/m3

x——干度

f——摩擦因子

Re——雷诺数

G——质量流率，kg/(m2·s)

S——熵产，W/K

v——比容，m3/kg

θ——优化参数

β——下降步长

下标 r——制冷剂侧

a——空气侧

in——内侧

ou——外侧

tu——管

w——壁面

fin——翅片

root——根部

b——半圆连接管

v——气相区

tp——两相区

i——进口

上标j——计算次数