定向钻穿越管道施工引起曹娥江堤防土层变形计算分析
殷学成,柴文琦,李树巍
(浙江省钱塘江管理局勘测设计院,浙江 杭州 310016)
1 问题的提出
随着经济的发展,近几十年来长距离输送油气、输水、通信等管道得到蓬勃发展,而定向钻穿越作为一种先进的非开挖管道穿越施工方法,因其施工时不会破坏水域堤防、对河床扰动少、施工期短、工程造价低等特点,在地质条件适宜的情况下,得以大规模应用于大中型河流穿越工程中[1]。
定向管道施工对地面建筑物及周围环境影响较小,但是仍会对周围土体产生扰动,从而引起地面变形。目前,对地下管道施工的研究踵事增华,其中顶管法和盾构法在理论和工程实践中得到大量的研究和应用[2-3],但是对定向钻管道施工引起的地面变形研究比较缺乏,多集中在定向钻管道的施工工艺和技术上,以及定向钻技术穿越河流的防洪评价分析[4-5]。
本文以定向钻管道穿越曹娥江工程为例,通过Plaxis软件数值模拟对管道施工引起的曹娥江堤防堤顶路面变形进行研究分析,并提出相应的预防措施。
2 Plaxis有限元软件简介
Plaxis软件是由荷兰PLAXIS B.V.公司研究开发的二维计算程序,被广泛应用于岩土工程的变形和稳定性研究中。该软件借助先进的本构模型,能够模拟土体的非线性、时间相关性和各向异性行为,还能考虑结构模型和土体与结构之间的相互作用等[6]。
Plaxis计算软件中主要通过线弹性模型和Mohr-Culomb模型模拟地基土[6]。
(1)线弹性模型。该模型参数中包含以下参数:抗弯刚度EI(kN · m2),轴向刚度EA(kN/m),重度w(kg/ cm3),厚度d(m),泊松比µ。
(2)Mohr-Culomb模型。模型中包括以下5个输入参数:土体弹性模量E(kPa)和泊松比µ,表示土体塑性的粘聚力C(kPa)和摩擦角φ(°),剪胀角ψ(°)。Mohr-Culomb模型屈服准则:
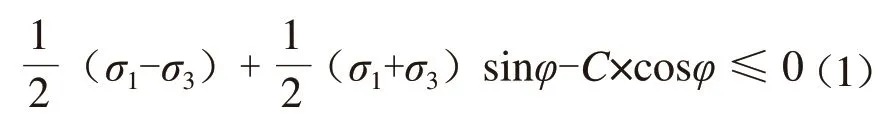
同时,该模型对塑性势函数进行了定义:

式(2)中:g为势函数包含第三个塑性参数,即剪胀角ψ。
3 工程实例
绍兴—杭州成品油管道工程(以下简称“绍—杭管道”)穿越曹娥江堤防某处,距离袍江大桥西80 m,采用管径φ406.4 mm直缝埋弧钢管,穿越长度约为1 210 m,右岸入土点距堤脚85 m,入土角取10°,左岸出土角距堤脚95 m,出土角取10°,穿越管段在曹娥江堤防下高程为-18.00 m,实际埋深约28.0 m。
3.1 计算工况及模型概化
该模型考虑的输油管道直径为600 mm(按扩孔孔径比拖管管径大50%考虑),管道穿越处流域水位高程取6.65 m,堤防高10.0 m。根据现场工程地质情况,工程管道穿越段地质分布自上而下分别为:1-1堤身素填土(层厚△H=5.5 m), 2-2砂质粉土(层厚△H=9.5 m),3-2淤泥质粉质黏土(层厚△H=19.6 m),4-1粉质黏土(层厚△H=5.1 m),4-2淤泥质粉质黏土 (层厚△H=4.8 m)。土体物理力学参数见表1。

表1 土体物理力学参数表
管道位于地下淤泥质粉质黏土中,为满足有限元理论位移协调的原则,需要在2种材料间加设界面单元,以此有效模拟钢管与土体之间的相对位移。钢管与土体的接触表面是介于完全光滑和完全粗糙之间,在Plaxis软件中可以通过设定界面强度折减因子Rinter来衡量[6]。该折减因子Rinter关系式为:
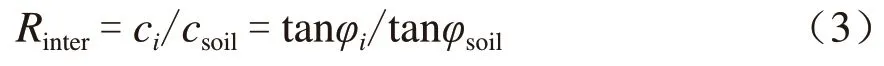
式中:ci和φi分别为界面的内聚力(kPa)和摩擦角(°);csoil和φsoil分别为土层的内聚力(kPa)和摩擦角(°);Rinter取0.7。
Plaxis数学模型采用15节点单元,共有866个单元,10 392个节点,以合适的边界条件加以模拟(见图1)。

图1 定向钻管道穿越曹娥江堤防有限元计算模型图
3.2 模型结果分析
定向钻管道施工造成地表轻微下陷,图2为定向钻管道施工引起的堤防地基土层竖直方向上的变形云图。从图2中可以看出,定向钻管道施工后,土层沉降对称分布,最大沉降出现在管道中心轴线位置,管道上方的土层沉降随深度的增加而增加,在接近管道顶端位置达到最大;而管道下方土体出现向上的位移,在管道底端达到最大。

图2 管道施工引起的堤防地基土层竖直方向上的变形云图
同时,研究文献7~8提出不排水固结的条件下,管道施工因土体损失而导致地面变形的计算方法。Peck给出的地面沉降横向分布的预估公式[7],在工程领域得到广泛应用。

式(4)~(5)中:S(x)为地面沉降量(m);x为离管道轴线的水平距离(m);Smax为管道轴线上方地面最大沉降量(m);V1为单位长度上的土体损失率(m3/m),主要与工程地质情况、管道施工方法与施工工艺等因素有关;i为沉降槽宽度系数(m),管道在黏土中埋深h满足3 m≤h≤34 m时,i的经验公式可表示为:

图3为Plaxis计算模型得到的堤顶路面沉降与水平距离的变化曲线,该变化趋势与Peck公式法一致。经过比较,Plaxis模型计算得到管道轴线位置的沉降最大值为1.73 mm,与Peck公式法得到的沉降最大值1.71 mm比较接近。
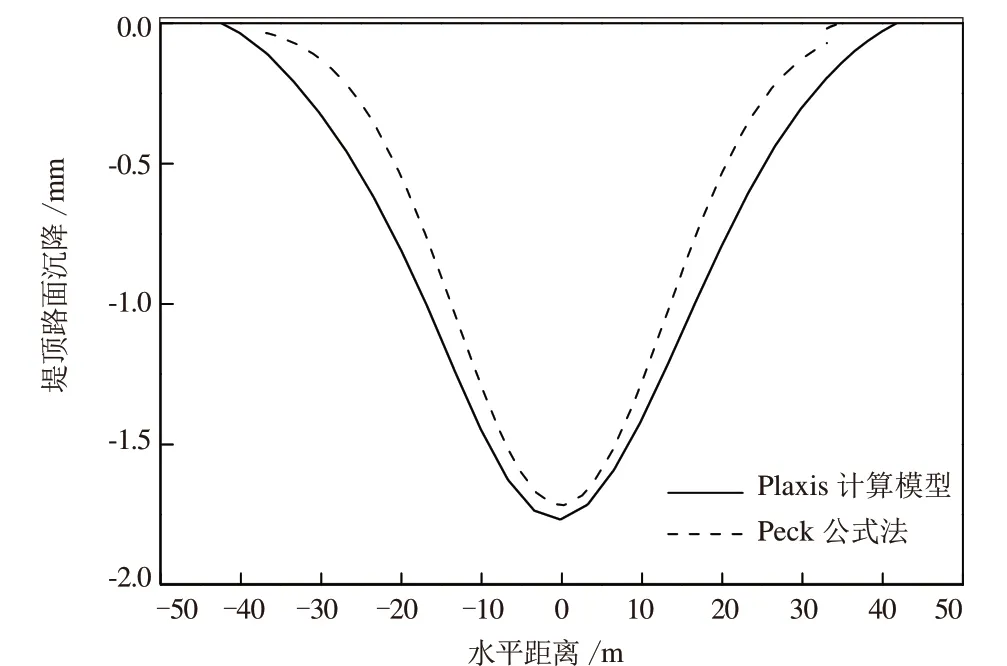
图3 Plaxis模型与Peck公式法堤顶路面沉降横向分布比较图
3.3 管道埋深改变时的堤顶路面沉降规律
本文设置定向钻管道埋深分别为5,10,15,20,25,30,35 m共7种情形来分析管道埋深对堤顶路面沉降的变化规律。数值计算的模型基本同图2,只是管道的原点坐标是变化的。图4~5为Plaxis数值模拟的计算结果。
图4为具有代表性的4种定向钻管道地下埋深变化时堤身土层竖向变形等值线云图。从图4上可以得出,当管道埋深变化时,堤身土层竖向变形的等值线云图形状及其等值线上的数值也会随之变化;经过比较发现,随着管道埋深变小,堤顶路面沉降随之变大。
由图5可以得到:1对于同一管道埋深,管道正上方的堤顶路面沉降最大;2图中所有曲线基本相交于2点(-28.0,-0.3)和(28.0,0.3);3在x轴的[-28,28]范围内,堤顶路面的沉降随着管道埋深的减小而增大,在[-50,-28]和[28,50]范围内,堤顶路面的沉降随着管道埋深的增大而增大。
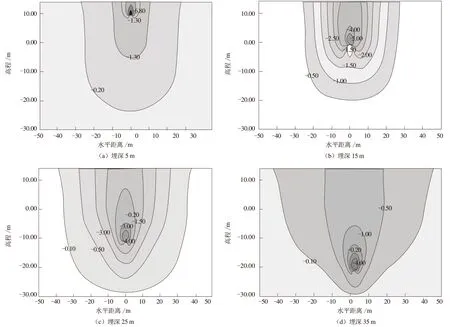
图4 管道埋深不同时的土层竖向位移云图
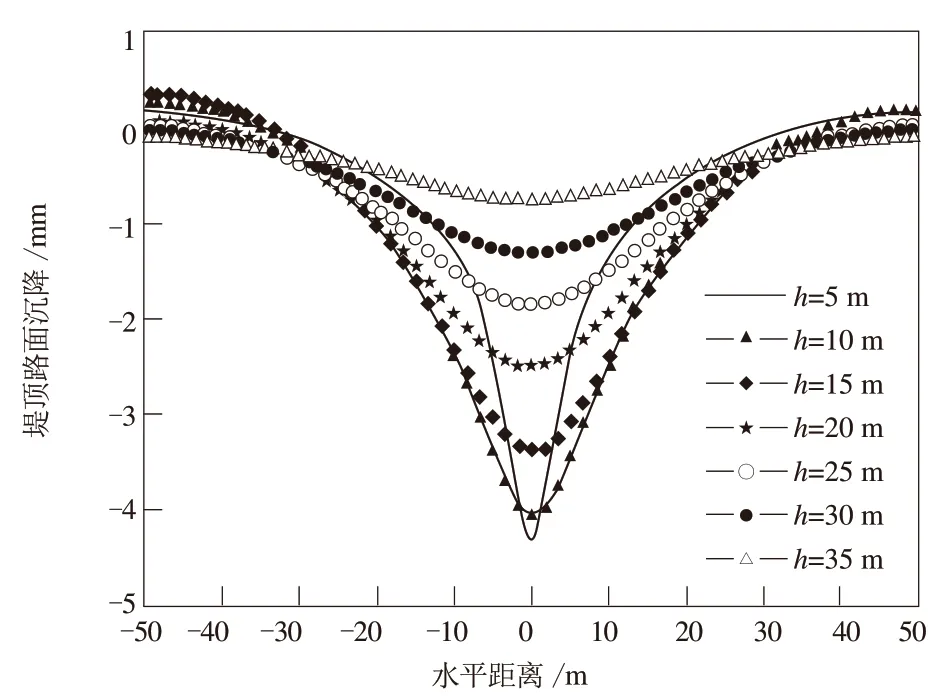
图5 管道埋深变化时堤顶路面沉降与水平距离关系图
4 结论与建议
(1)通过Plaxis数值模拟定向钻管道穿越曹娥江堤防,结果表明定向钻管道施工会引起土层在竖直方向的位移变化,最大沉降出现在管道中心轴线位置;并与Peck经验公式法比较可知,堤顶路面的最大沉降相比经验公式法略大,因为Plaxis模型适应复杂边界调节和地层结构,其计算结果较Peck经验公式更为合理。
(2)对于同一管道埋深时,管道轴线正上方的堤顶路面沉降最大;管道埋深变化时,堤顶路面最大沉降与管道埋深的深度呈现负相关关系。因此,在曹娥江定向钻管道时,要严格控制管道埋深,以控制合理的堤顶路面沉降。
(3)为将定向钻管道穿越曹娥江堤防产生的沉降控制在合理范围内,除了建立现场沉降变形监测系统,还应采用平衡功能较好的定向钻机,减少减阻泥浆套的厚度,严格控制出泥量,定向钻结束后采用水泥砂浆加固减阻泥浆等措施;同时,施工过程中应根据不同穿越地层和深度,适当调整泥浆的工作压力和排量,防止由于泥浆压力和性能改变造成泥浆漏失,减少由于冒浆诱导产生地层裂缝的可能性。
(4)得出的堤顶路面沉降规律对穿越曹娥江流域堤防的管道施工有一定的参考价值。

