农业用水统计方法改进的探索与实践以丽水市为例
沈春玲,戚核帅,温进化
(1.丽水市水利局,浙江 丽水 323000;2.浙江省水利河口研究院(浙江省海洋规划设计研究院),浙江 杭州 310020)
1 问题的提出
用水总量统计是水资源管理的常规工作,各级地方水利部门每年都要开展用水量分析、统计、校核等工作,并定期向社会发布。同时,用水总量统计成果也是各地落实最严格水资源管理制度用水总量目标考核的重要依据。以丽水市为例,农业用水量约占全市用水总量的64.7%,农业用水量统计是丽水市用水总量统计的重点。但在南方丰水地区,灌区一般都存在水源数量多、水源供水随机性强等特点,且受水资源监控计量设施建设资金少及后期运行管理难度大等因素制约,要按照办资管〔2020〕76号《关于做好用水统计调查制度实施工作的通知》要求,对灌区水源供水量进行全面监控进而精确统计农业用水量,存在较大的难度。
目前,农业用水统计方法主要可分为2类[1]:一是基于监测数据的统计分析,多数采用典型调查或现行灌溉定额与实灌面积进行匡算[2],是目前用水统计工作中最常用的方法;二是基于水循环过程的物理模型方法,常见的有SWAT模型[3]等,但建模对灌区基础资料的支撑情况具有较高要求。根据丽水市灌区管理的实际情况,普遍采用以农田灌溉水有效利用系数测算等为依据的定额推算方式,但现行测算统计工作主要基于典型渠段或田块推算得到灌区水量,由于灌区渠系的多样性和复杂性,难以反映事物的全貌[4],统计方式相对粗放。
本文以丽水市为例,基于农田灌溉水有效利用系数测算等样点灌区数据成果,在分析筛选农业用水量主要影响因素的基础上,结合气象水文、种植结构、管理实际等情况引入相应影响系数,对传统灌溉定额推算方法进行改进,提出丽水市农业用水统计方法,为同类型地区农业用水统计工作提供参考。
2 研究区域概况
丽水市地处浙江省西南浙闽两省结合部,位于东经118º41′~120º26′、北纬27º25′~28º57′。东南与温州市接壤,西南与福建省宁德市、南平市毗邻,西北与衢州市相接,北部与金华市交界,东北与台州市相连。属亚热带湿润季风气候,热量丰富,降水充沛,四季分明。
丽水市均为中小型灌区,以自流型灌区为主。其中,3 333.3~10 000.0 hm2的中型自流灌区2处,666.7~3 333.3 hm2的中型自流灌区8处,666.7 hm2以下的小型自流及提水灌区共有3 843处。全市有效灌溉面积为95 066.0 hm2,以种植水稻为主,主要农作物还包括豆类、薯类、油菜籽、药材、蔬菜、瓜类等。
3 改进思路
参考美国采用的灌溉面积×灌溉定额估算,综合考虑不同作物的耗水差异、气候条件等不确定因素的方法[5],通过影响因素分析与筛选,对传统定额法进行改进,提出适用于丽水市实际情况的农业用水统计方法。
3.1 数据来源与处理
选取丽水市19个样点灌区作为研究数据来源。由于灌区基础条件基本维持稳定,且同一区域内灌溉技术及管理水平也基本相当,结合数据获取的可靠性以及实际管理的可行性,选取近5 a(2014—2018年)有效灌溉面积、播种面积、降水深、代表灌区基础条件的农田灌溉水有效利用系数、代表丽水市种植结构特征的水稻种植面积、茶叶种植面积、蔬菜种植面积、其他种植面积作为数据样本,并对其进行无量纲化处理。各样点灌区基本情况见表1。
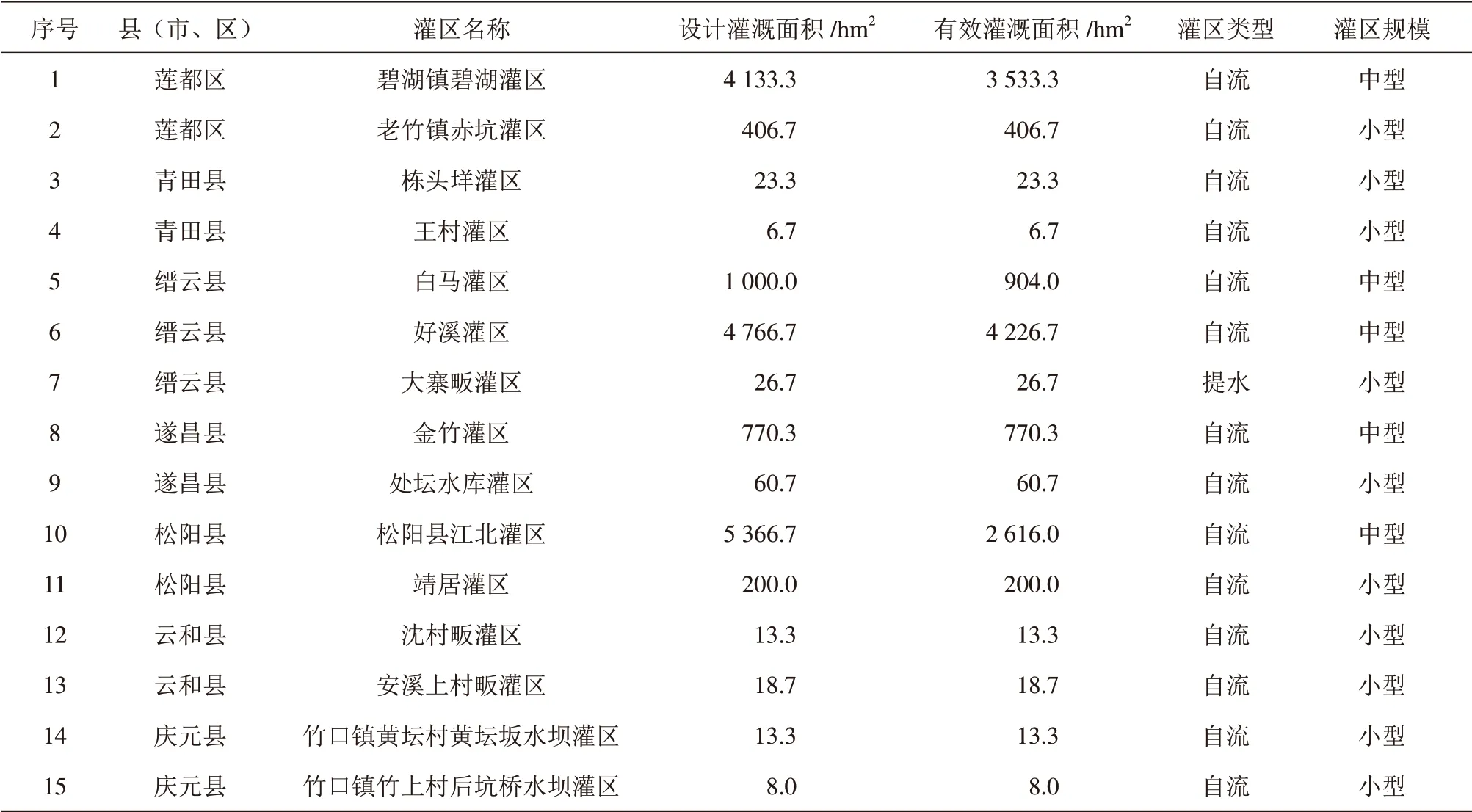
表1 丽水市样点灌区基本情况表

续表1
3.2 影响因素分析
目前农业用水影响因素分析的常用方法有多元线性回归法和Tobit模型等。首先采取全要素分析的方式,将选取的全部影响因素纳入分析样本,然后在全要素分析结果基础上,结合影响因素物理意义的判断,通过样本筛选组合分析后,得到农业用水主要影响因素。
3.2.1 多元线性回归法
多元线性回归[6]是计量经济学里最基本的回归方法,是利用线性回归方程的最小平方函数对多个自变量和因变量之间关系进行建模的一种回归分析,应用于经济、水文、气象等多个领域,是目前应用广泛的回归分析方法。
以二元线性回归模型为例:

式中:Y为因变量;X为自变量;b为对应变量的回归系数。
3.2.2 Tobit模型
Tobit模型[7]是美国诺贝尔经济学奖获得者James Tobin在分析家庭耐用品支出情况时对Probit回归进行的一种推广,能够很好地解决受限或截断因变量的模型构建问题,在农业用水效率的影响因素分析中广泛应用。
Tobit模型如下:

式中:Y、Y*为因变量;X为自变量;α为截距项;β为未知参数;ε为扰动项。
3.3 统计方法改进
根据农业用水影响因素的影响特征关系,引入水文特征系数、种植结构系数、管理水平系数等,以适用不同年型、不同区域、不同种植结构的情况,提升方法的通用性与可靠性。改进定额法的一般表达式如下:

式中:W为区域农业用水量,万m3;f1、f2、f3分别为水文特征系数、种植结构系数、管理水平系数;S为区域灌溉面积,万hm2;Q为平均灌溉用水量,m3/hm2。
根据农业用水影响因素的物理特征,结合管理实际和数据量化情况,确定水文特征系数、种植结构系数和管理水平系数的指标定义如下:
(1)水文特征系数采用蒸发降水比,即蒸发强度与降水深度之比。
(2)种植结构系数采用体现水稻种植结构特征的指标,为保证统计指标的规范合理性,以及规避全是水稻种植或全非水稻种植的情况,以“(播种面积+水稻种植面积)/播种面积”作为计算指标。
(3)基于数据获取和数据量化的考虑,采用农田灌溉水有效利用系数的倒数作为管理水平 系数。
4 结果与分析
4.1 农业用水量影响因素分析
4.1.1 全要素分析
多元线性回归法全要素分析结果见表2;Tobit模型法全要素分析结果见表3。
由表2~3可知,2种方法在全要素分析中呈现出较大分歧。其中,多元线性回归法中播种面积(相关性弱)、有效灌溉面积(P>|t| =0.068)、茶叶种植面积(P>|t|=0.814)呈现非显著性的影响程度;Tobit模型法中有效灌溉面积(P>|t|=0.056)、水稻种植面积(P>|t|=0.566)、其他作物种植面积(相关性弱)呈现非显著性的影响程度。

表2 多元线性回归法全要素分析结果表
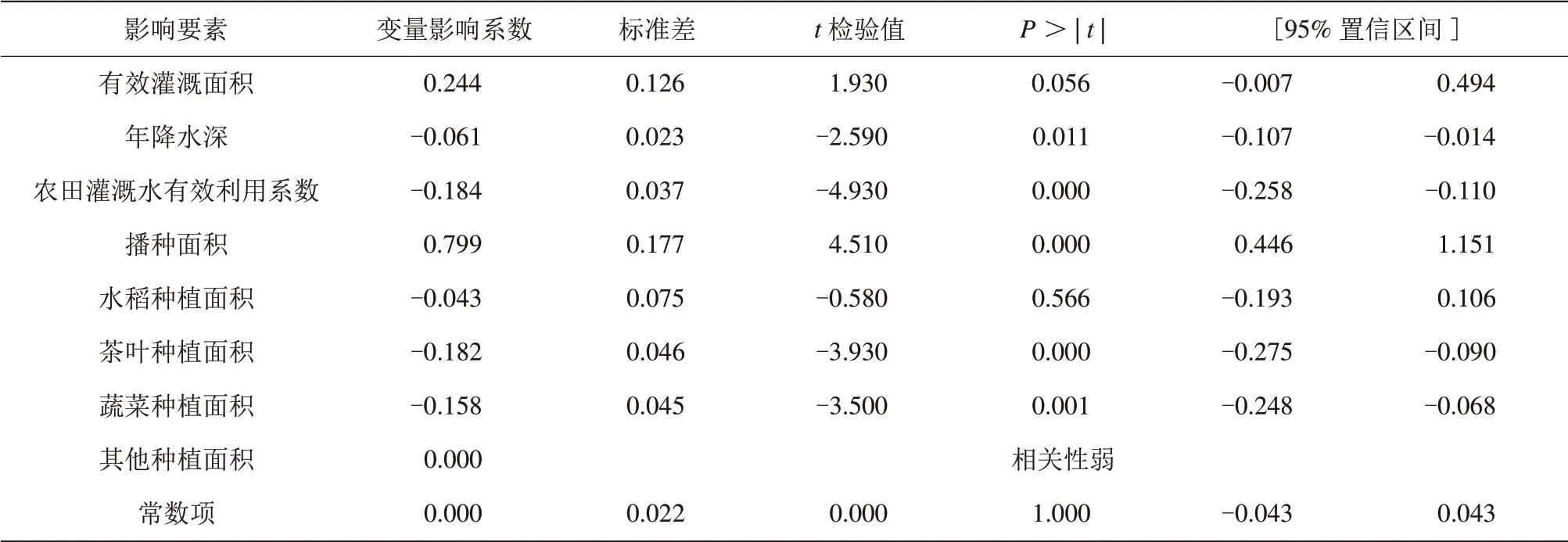
表3 Tobit模型法全要素分析结果表
4.1.2 主成分要素分析
经样本筛选组合后,以有效灌溉面积、年降水深、农田灌溉水有效利用系数、播种面积、水稻种植面积为主成分要素,分析如下:
多元线性回归法主成分要素分析结果见表4,Tobit模型法主成分要素分析结果见表5。
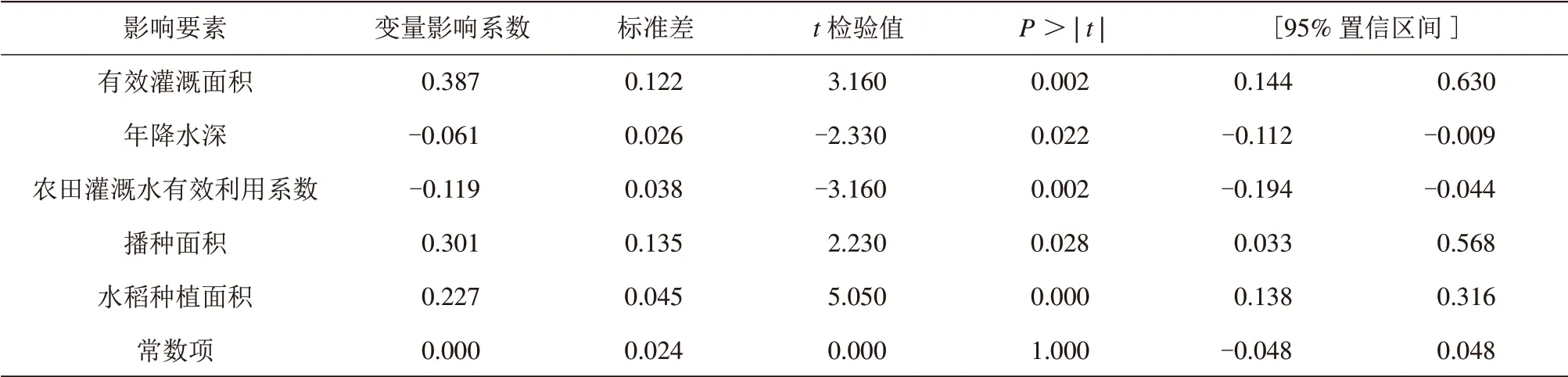
表4 多元线性回归法主成分要素分析结果表

表5 Tobit模型法主成分要素分析结果表

续表5
由表4~5可知,对于主成分要素的影响因素分析,2种方法表现出较高的一致性。根据P>|t|指标的分析,各主成分要素都呈现出较为显著的影响程度,其中年降水深和播种面积要素的影响程度相对偏弱。根据变量影响系数指标的分析,农业用水量与有效灌溉面积、播种面积、水稻种植面积呈正相关影响,而与年降水深、农田灌溉水有效利用系数呈负相关影响,并且有效灌溉面积是农业用水量最主要的影响因素。
4.2 农业用水量统计分析
以农业用水量主要影响因素作为统计分析样本,采用改进定额法,利用Stata软件进行模型构建和求解,得到丽水市农业用水量改进定额统计模型如下:
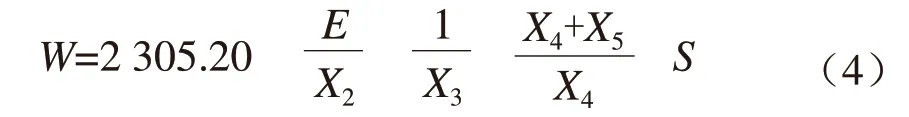
式中:W为区域农业用水量,万m3;X2为年降水深,mm;E为蒸发量,mm;X3为农田灌溉水有效利用系数;X4为播种面积,万hm2;X5为水稻种植面积,万hm2;S为有效灌溉面积,万hm2。
根据丽水市农业用水量统计结果(见图1),分别采取“全市统计”和“典型测算+非典型统计”2种方式,对比分析丽水市水资源公报2014—2018年农业用水量得到:统计结果年际间呈现一定偏差,但总体尚可,平均统计偏差在-8.0%左右;研究采取的2种统计方式,统计结果基本一致。
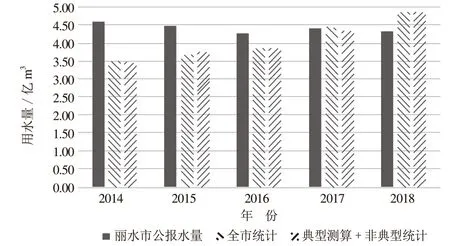
图1 丽水市农业用水统计结果对比图
5 结 语
本文在用水影响因素分析和定额改进的基础上,通过基于丽水市样点灌区数据的农业用水量统计方法的探索与实践,得到主要结论如下:1农业用水量受水文特征、种植结构、管理水平等密切影响,采用多元线性回归法和Tobit模型法对影响因素的影响显著性分析,可较好地确定影响区域农业用水的主要因素;2通过引入水文特征系数、种植结构系数、管理水平系数等影响系数提出的农业用水改进定额统计法,总体表现较好,可为丽水市农业用水统计工作提供支撑。

