不同糙体对水流和糙率特性影响试验研究

江会昌，吴军君

（浙江省钱塘江管理局勘测设计院，浙江 杭州 310016）

1 问题的提出

不同糙体对水流特性的影响不同，使得加糙后所能达到的糙率也不尽相同，这也是不同的河工模型选取不同糙体和加糙方式的原因。针对淮河干流淮正段的大变态非恒定流河工模型要求的糙率较大情况，一般糙体难以达到阻力相似的目标。陈先朴等[1]设计并论证梅花形十字板加糙；华北水利水电学院[2]结合工程实际需要提出用塑料草垫加糙的方法；为解决定床潮汐河工模型加糙的难题，陈志昌等[3]提出采用等腰三角橡皮块加糙的方法；徐华等[4-5]通过水槽试验推导出三角块梅花形加糙后的糙率计算公式；朱代臣等[6-7]研制Y型塑料加糙体用于长江防洪模型试验，并取得满意的成果。

然而，一直以来许多专家学者都比较关注加糙后所能达到的糙率，却没有进行糙体本身对水流特性影响方面的分析和探讨。本文选取2种不同糙体进行水槽试验，利用美国SonTek公司研制的三维声学多普勒流速仪（Micro Acoustic Doppler Velocimeter，简称ADV）进行多工况流速量测，从流速、紊动强度和雷诺应力等垂向与横向分布着手，分析不同糙体、布置方式、流量及水深变化对水流特性的影响，探讨糙率与雷诺数及弗劳德数之间的关系，以期认识不同糙体加糙后对水流特性的影响特征，进而了解糙体的阻力特性，为选择糙体提供技术参考。

2 试验装置与方法

2.1 试验装置

本试验在多功能水槽中进行，水槽长35.0 m，宽0.8 m，高1.0 m，其中有效长度32.0 m。为尽可能减少进出口对试验的影响，保证水流平稳过渡，进口、出口段各长7.0 m，加糙试验段长18.0 m。加糙试验水槽见图1，槽底、边壁均为有机玻璃。

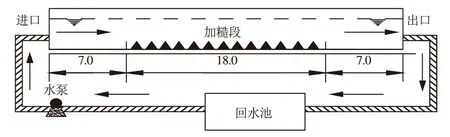
图1 加糙试验水槽示意图 单位：m

试验选用的糙体为光壁石和塑料草2种，其中光壁石的等容粒径（d）为1.75～2.12 cm，塑料草高约2.0 cm。先在水槽内铺设1块厚约6.0 mm的PVC塑料板，再用AB胶将糙体按梅花形布置粘贴在PVC板上。利用ADV进行垂线流速测量，流速仪的采样频率为25 Hz，每个测点持续测速30 s，并通过Win ADV平台处理试验数据。

2.2 试验方法

试验分为3种不同水深，分别是15.0，20.0，30.0 cm，在相同的水深条件下通过增大流量来增加流速，通过自动控制系统调节满足水深基本不变，试验工况见表1。

试验时，在水深小于2.0 cm的范围内每隔2.0 mm测量1个点，2.0～4.0 cm之间每4.0 mm测量1个点，4.0 cm以上每1.0 cm测量1个点。在试验段的正中间布设5条测流垂线（自左至右间距 分 别 为0.10 ，0.15，0.15，0.15 ，0.15 ，0.10 cm），利用ADV测量各工况条件下的流速，以分析时均流速、紊动强度和雷诺应力的垂向与横向分布特征。

表1 试验工况表

3 试验结果与分析

3.1 流速分布特征

图2～4展示了3种试验工况的流速垂向和横向分布。由图2～4可知，糙体对水流的流速分布有着重要影响。加糙后流速垂向分布呈“J”型，相同参数条件下加糙间距、水深越小，流量越大，流速分布“J”型越明显，其对水流的干扰作用也就越强，同时水流在糙体有效高度范围内，流速变化就越大。塑料草对流速垂向分布的影响较光壁石大，相对于加糙间距和水深，流量变化对流速的垂向分布影响更大。

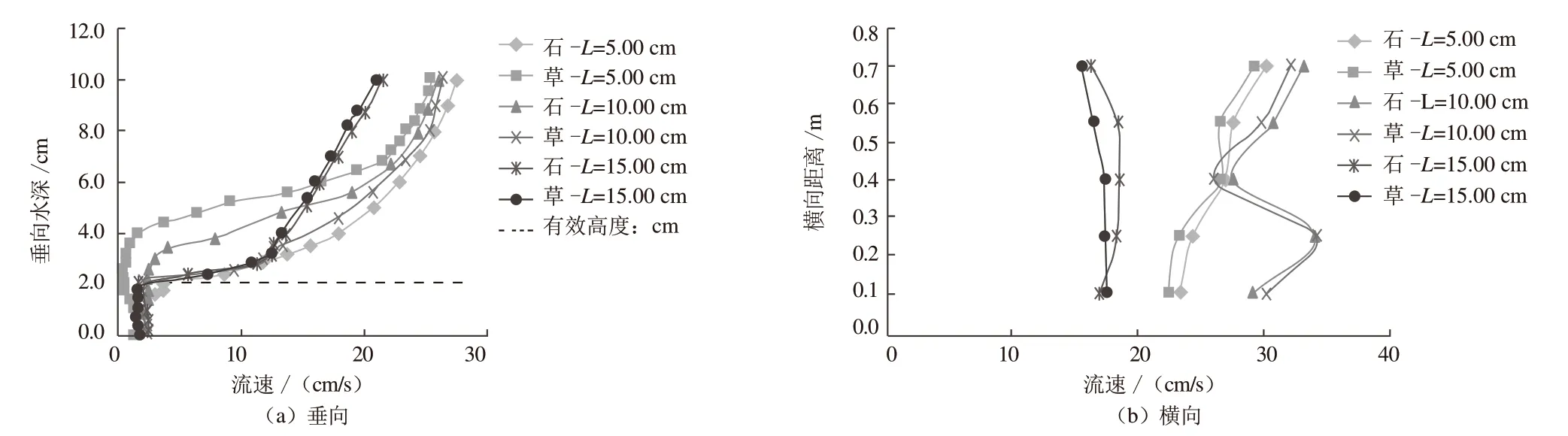
图2 工况1流速分布图

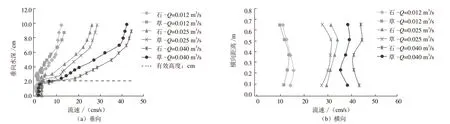
图3 工况2流速分布图

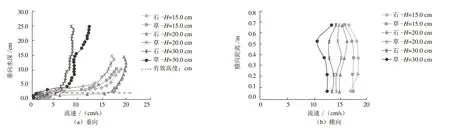
图4 工况3流速分布图

3.2 紊动强度分布特征

脉动流速是水流紊动的最重要特性之一，其均方根被称为紊动强度[8-9]。本文主要考虑糙体对纵向水流紊动强度的影响，在Win ADV中其数据处理的计算公式为：

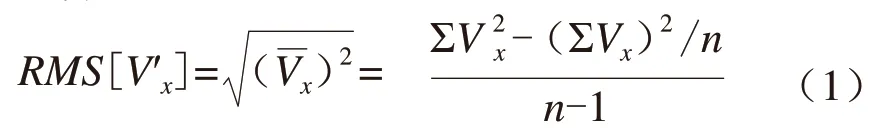
式中：Vx为纵向瞬时流速，cm/s；n为统计样本个数，无量纲。

图5～7展示了各种试验工况紊动强度的垂向和横向分布。由图5～7可知，糙体对水流的紊动强度也有重要影响。加糙后水流的紊动强度分布呈现不同程度的变化，相同参数条件下加糙间距越大、流量越小、水深越大，其紊动作用越弱。塑料草对紊动强度的影响较光壁石大，这是因为塑料草的表面比光壁石还要“粗糙”，塑料草有许多分支，且本试验选用的草是柔性的，随水流易弯曲、波折，从而导致紊动强度更大。总体上紊动强度垂向分布略呈斜“J”型，在有效高度内由于糙体自身的绕流作用导致紊动强度增大，相对于水深变化对2种糙体加糙后紊动强度的影响，流量与加糙间距的影响更大一些；通过比较流速分布图和紊动强度分布图，可以发现，流速与流速梯度变化越大的地方，紊动强度越大，这与前人[7]的研究结果一致。

图5 工况1紊动强度分布图

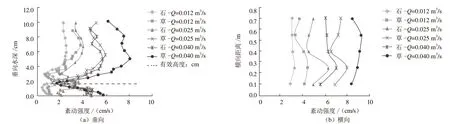
图6 工况2紊动强度分布图

图7 工况3紊动强度分布图

3.3 雷诺应力分布特征

雷诺应力是紊动水团的交换在流层之间产生的剪切应力[10]，是表征水流结构变化的一个重要参数，源于流场在空间上的不均匀性，代表紊流脉动对时均流动的影响，最终的作用结果是使流动均匀化。为方便分析，本文采用x、z方向的雷诺应力作为代表，其表达式为：

式中：ρ为水的密度，1 g/cm³；ux′为x方向的脉动速度，cm/s；uz′为z方向的脉动速度，cm/s。

图8～10为各工况雷诺应力分布图。由图8～10可知，糙体对雷诺应力的分布也有重要影响，加糙后雷诺应力分布呈现出不同程度的变化，加糙后其垂向分布总体上呈“>”型；在相对水深（水深/有效高度）约为5.0处有最大值，且塑料草的最大值比光壁石的大，因为塑料草的柔性大于光壁石的柔性的结果；相同参数条件下加糙间距越小、流量越大、水深越小，雷诺应力的最大值就越大。

图8 工况1雷诺应力分布图

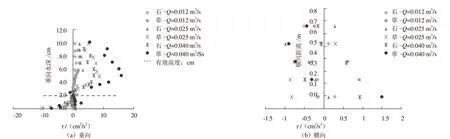
图9 工况2雷诺应力分布图

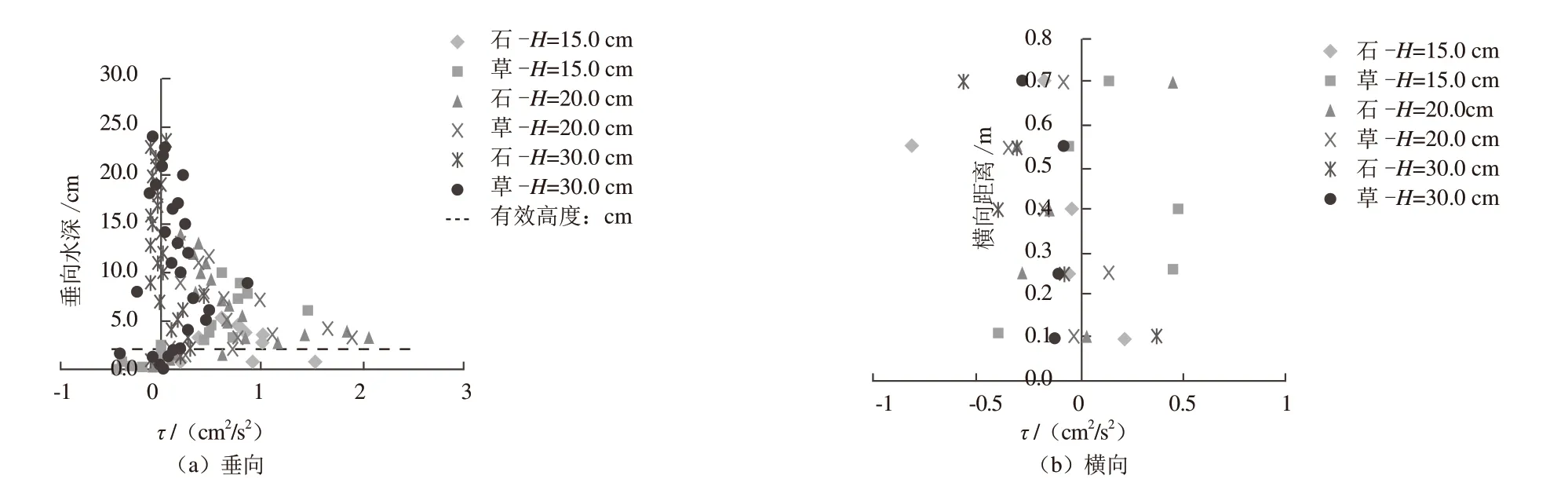
图10 工况3雷诺应力分布图

4 糙率的变化特性

4.1 加糙间距对糙率的影响

加糙间距变化对糙率的影响见表2。糙率是反映水流阻力影响的一个综合性无量纲数，一般用n表示，糙率值采用曼宁公式计算：

式中：i为水力坡降，无量纲；R为水力半径，m；A为过水断面面积，m2；Q为流量，m3/s。

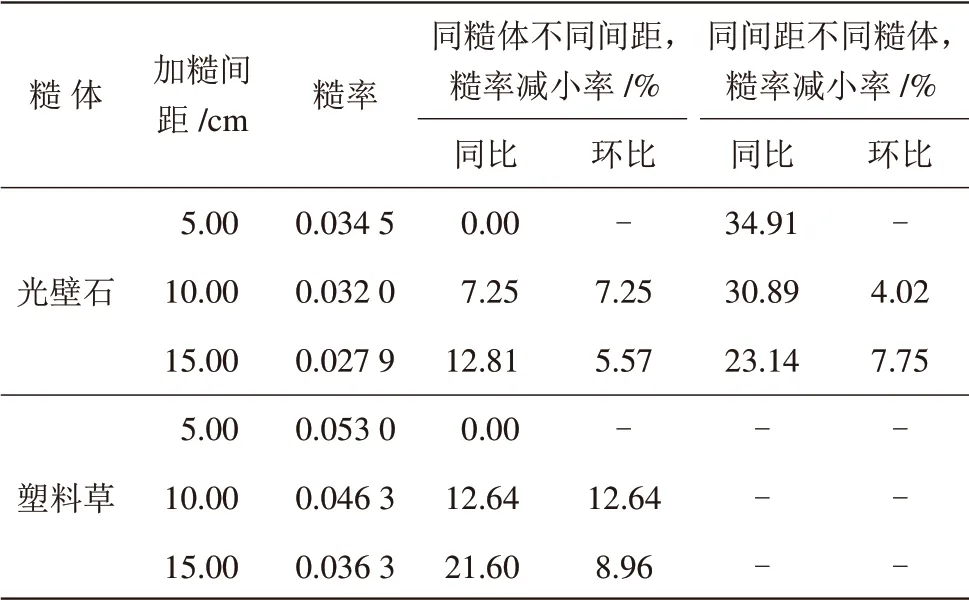
表2 加糙间距变化对糙率的影响表

从表2可以看出：1塑料草加糙后的糙率比光壁石大。2在保持流量和水深不变的情况下，随着加糙间距的增大，糙率逐渐减小，最后趋于定值，但塑料草糙率减小的趋势比光壁石明显，塑料草糙率下降的梯度较光壁石大。3光壁石加糙后的糙率减小率相对于塑料草小，且塑料草加糙后糙率下降的速度较快，但两者的减小趋势在逐渐变缓；另外，两者加糙后的糙率趋于一致的速度在变大。

4.2 流量对糙率的影响

流量变化对糙率的影响见表3。

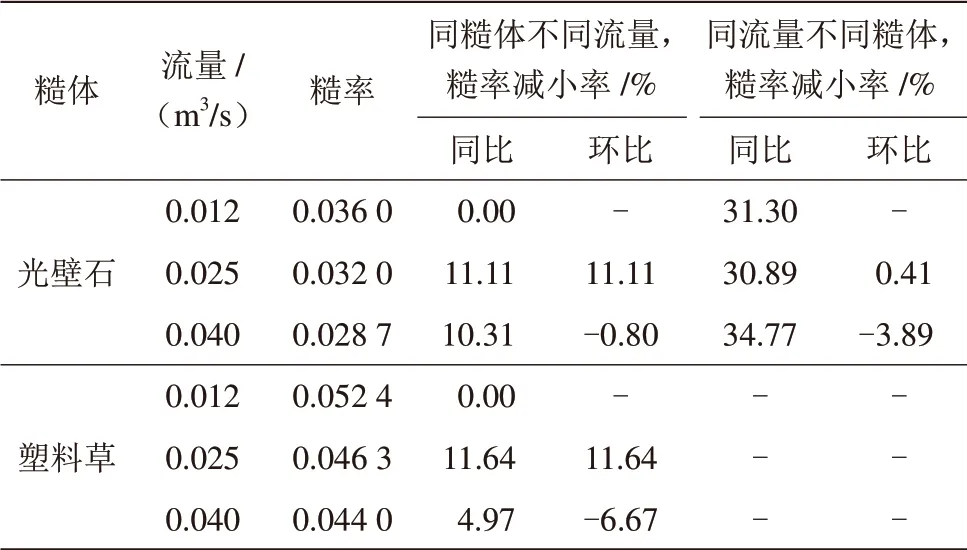
表3 流量变化对糙率的影响表

从表3可以看出：1塑料草加糙后的糙率比光壁石大。2在保持水深和加糙间距不变的情况下，随着流量增大，糙率逐渐减小，但塑料草糙率减小的趋势越来越小，最后趋于定值，而光壁石的糙率几乎直线下降。3在一定范围内，光壁石加糙后的糙率减小率相对于塑料草小，当超过这一范围时，其下降的速率反而较塑料草大；两者加糙后的糙率趋于一致的速度在一定范围内随流量的增大而变大，超出这一范围时反而呈减小趋势。

4.3 水深对糙率的影响

水深变化对糙率的影响见表4。

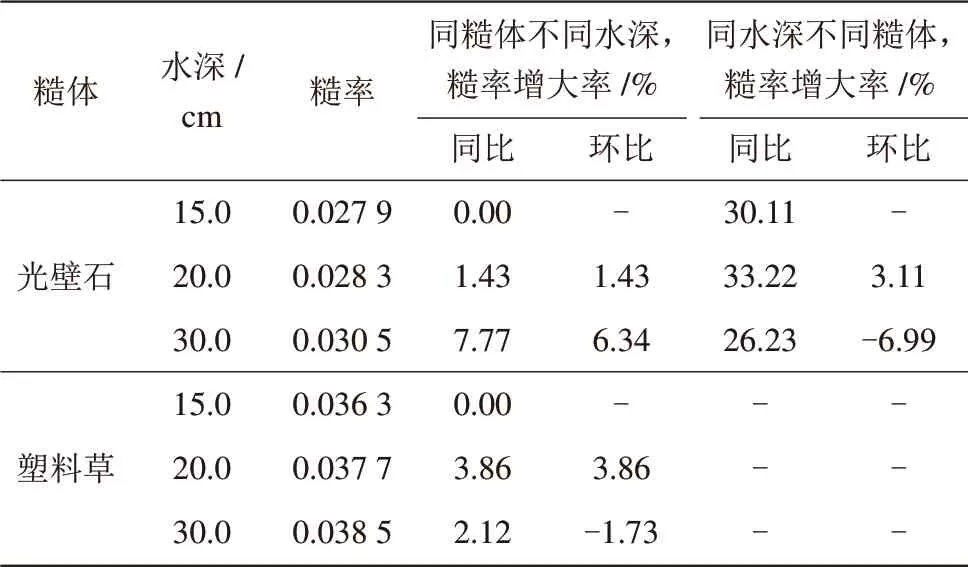
表4 水深变化对糙率的影响表

从表4可以看出：1塑料草的糙率比光壁石大。2在保持流量和加糙间距不变的情况下，随着水深的增加，糙率逐渐增大，塑料草糙率增大的趋势越来越小，而光壁石却相反，增大的趋势略显增加。这可能是因为光壁石水位抬高值较大，尤其是在低水位的时候更明显，水深修正导致糙率变化突出。3在一定范围内，光壁石加糙后的糙率增大率相对于塑料草小，当超过这一范围时，其增大的速率反而较塑料草大；两者加糙后的糙率趋于一致的速度在一定范围内，随水深的增加而变小，超出这一范围时，趋同的趋势就越来越明显。

4.4 糙率与雷诺数（Re）、弗劳德数（Fr）之间的关系

光壁石糙率随雷诺数、弗劳德数的变化见图11。

从图11（a）可以看出：1随着雷诺数增大，糙率逐渐减小，但变化幅度越来越小，最后趋于稳定。2试验条件下糙率变化范围为0.025 4～0.038 6。不同加糙间距所能达到的糙率值不同，加糙间距为15.00 cm时糙率小于0.030 6，间距为10.00 cm时糙率为0.028 7～0.036 0，间距为5.00 cm时糙率大于0.033 2。由图11（b）可知光壁石糙率随弗劳德数的变化规律与雷诺数相同。

塑料草糙率随雷诺数、弗劳德数的变化关系见图12。

图11 光壁石糙率随雷诺数、弗劳德数的变化图

图12 塑料草糙率随雷诺数、弗劳德数的变化图

从图12（a）中可以看出：1随着雷诺数的增大，糙率逐渐减小，但变化幅度越来越小，最后趋于稳定。2试验条件下糙率变化范围为0.034 6～0.057 1。不同加糙间距所能达到的糙率值不同，加糙间距为15.00 cm时糙率小于0.042 9，间距为10.00 cm时糙率为0.044 0～0.052 4，间距为5.00 cm时糙率大于0.051 7。由图12（b）可知塑料草糙率随弗劳德数的变化规律与雷诺数相同。

5 结 语

通过水槽试验及结果分析[11]，可得出光壁石和塑料草加糙后水流和糙率的变化特性：

（1）光壁石和塑料草对水流特性的影响及其糙率的变化规律相似，但塑料草对水流特性的影响较光壁石大，加糙后的糙率也比光壁石大。

（2）相同参数条件下加糙间距、水深越小，流量越大，流速呈“J”型分布越明显、紊动作用也越强、雷诺应力的最大值就越大；流量的变化相对于加糙间距和水深来说，其对纵向流速垂向分布的影响更大一些。而相对于水深的变化对纵向紊动强度垂向分布的影响，流量与加糙间距的影响更大 一些。

（3）在保持流量和加糙间距不变的情况下，随着水深的增加糙率逐渐增大。而保持水深和加糙间距不变，随着流量的增大糙率却逐渐减小。维持流量和水深不变，随着加糙间距的增大糙率也逐渐 减小。

（4）随着雷诺数或弗劳德数的增大，糙率逐渐减小，但幅度越来越小，最后趋于稳定。

（5）糙体对水流特性的影响十分复杂，本文仅通过水槽试验进行流速、紊动强度和雷诺应力等垂向与横向分布的初步研究，全面了解其影响机理还有待更多研究者进行深入研究。