嵊泗县暴雨强度公式推求
虞佳维,陶烨明,李可鹏
(嵊泗县气象局,浙江 嵊泗 202450)
1 问题的提出
嵊泗县地处亚热带季风气候区,由于独特的地理位置和气候条件,经常受梅雨、强对流天气和热带气旋(台风)的影响,是洪涝、台风、暴雨等气象灾害多发、重发地区,城区往往因排水不畅造成局部被淹引起内涝。近几年,受全球气候变化影响,极端气象灾害越来越频繁,暴雨天气频发,其中周北平等在2016年通过研究近53 a长三角地区极端降水时空变化分析发现,浙江东部沿海及岛屿站点的降水变得较为极端,未来易发生暴雨和洪涝,呈现出短时间局地性强降水集中的特征[1],加之目前短时临近暴雨预报预警能力较弱,尤其是强降水的定时、定点、定量精细化预报水平不足[2],一旦发生短时强降水将直接影响人民群众的生命财产安全及社会稳定[3-5]。
暴雨强度公式是科学、合理地制定城市排水工程规划、设计的基础,开展相关研究具有重要意义。嵊泗县无本县暴雨强度公式,主要采用舟山市暴雨强度公式作为本地暴雨强度公式,但由于嵊泗县距离舟山本岛较远,舟山市暴雨公式无法适应于本地。随着社会进步,迫切需要利用最新的实测资料编制嵊泗县城市暴雨强度公式,从而加强县域暴雨精细化监测预警工程建设,切实增强基层现代化水平和气象监测预警能力建设。
2 资料来源和统计样本选取
2.1 资料来源
所用资料源于嵊泗县国家基准气候站1980—2015年共36 a气象年报表中的暴雨雨量记录和降水自记纸资料、现代自动气象站逐分钟降水量资料。
2.2 统计样本建立
暴雨样本资料的选样方法有年最大值法、年超大值法、年超定量法与年多个样法等[6]。根据目前国家标准GB 50014—2006《室外排水设计规范》(2014年版)[7],具有20 a以上自动雨量记录的地区,排水系统设计暴雨强度公式应采用年最大值法,因此按照“不漏场次、不漏大值”的原则选取降雨过程,使用年最大值法编制暴雨公式。
本文选取每年5,10,15,20,30,45,60,90,120,150,180 min共计11个降水历时的年最大值作为建立暴雨强度公式的统计样本。重现期采用1,2,3,5,10,20,50,100 a等8个期限。
3 嵊泗县短历时降雨量年际变化特征
许多文献[1-5]中均指出全球极端天气越来越频繁,并且极端性越来越明显,由于仅在暴雨天气发生频率变化不大的情况下,得到的暴雨强度公式才具有现实意义,因此为确定嵊泗县暴雨天气发生情况,将嵊泗国家基准气候站1980—2015年共36 a的各历时分为1980—1997年和1998—2015年2段(2段均为18 a)综合分析暴雨发生情况以确定暴雨强度公式是否适用于外推的时间。对这2段各历时暴雨数据进行分析,统计排名前10的降水极值在2个时段内所占次数。根据数据显示,强降水事件在2个时段中出现的频率变化不大,但各时刻历史极值基本出现在后18 a内(见表1)。从表1中可以得出,1980—1997年的18 a中雨量最大的10个降水极值出现次数为4~7次,与1998—2015年的18 a中出现的3~6次基本相当。表2为1980—1997年与1998—2015年2阶段极端降水的样本均值对比表。由表2可知,前30 min后者最大降水均值均小于前者最大降水均值;在30 min以上降水历时,除120 min外,后者最大降水均值大于前者最大降水均值,但相差比例较小。
从统计结果可以得出,1980—2015年共36 a期间,强降水事件发生频率变化不大,较为平稳,30 min以下短历时极端降水量呈下降趋势,但30 min以上(除120 min外)累计降水量呈增加趋势。

表1 1980—2015年各历时最大的11个降水极值分布表
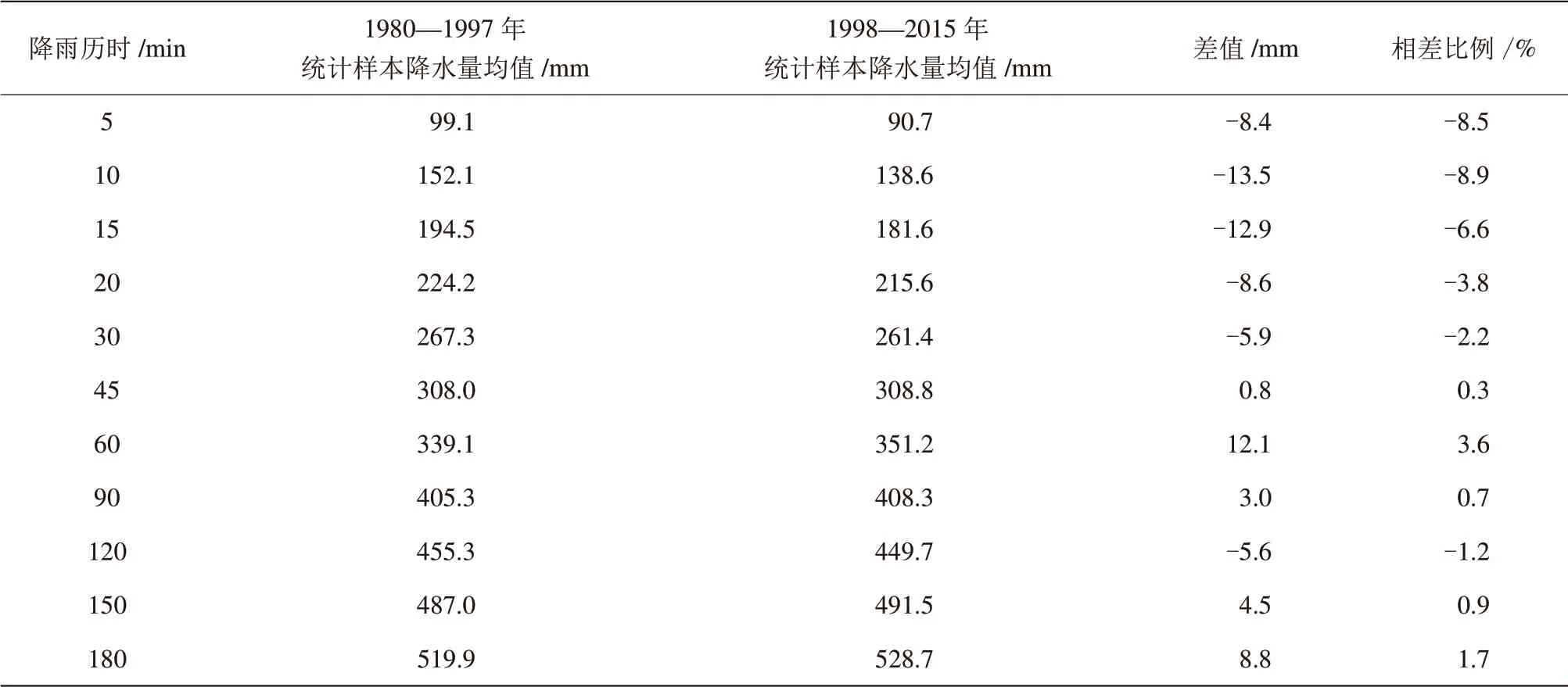
表2 1980—1997年与1998—2015年极端降水的样本均值对比表
4 频率计算和分布曲线拟合
4.1 频率和重现期计算[8]
在暴雨强度频率的计算中,常用经验频率公式:

式中:ρ为经验频率(%);n为样本总量;m为样本序号。
暴雨强度重现期p是指相等或超过暴雨强度出现1次的平均时间。由此得出重现期计算公式为:

式中:P为重现期(a)。
4.2 频率分布曲线拟合方法
频率分布曲线拟合基于选取的统计样本,采用经验频率曲线或理论频率曲线进行趋势性拟合调整。由于采用的重现期(100 a一遇)大于资料年限,故采用理论频率分布曲线对观测资料序列进行调整。暴雨强度公式统计中,常用的理论频率曲线有皮尔逊Ⅲ型分布曲线、指数分布曲线、耿贝尔分布曲线、经验频率曲线等。皮尔逊Ⅲ型曲线(简称P-Ⅲ型)是一条一端有限一端无限的不对称单峰、正偏曲线,通过“适线法”调整公式中的变差系数Cv和偏态系数Cs,使理论频率曲线与实际频率曲线基本吻合,指数分布曲线是基于X=a×1nT+b,耿贝尔分布曲线是基于X=-a×〔1n{1n[p/(p-1)]}〕+b。
选用何种分布曲线关键是看分布曲线对原始数据的拟合程度,误差越小、精度越高的分布越具有代表性,拟合精度以绝对均方误差和相对均方误差作为判断标准[9]。利用中国气象局推广下发的“暴雨强度计算系统”对频率分布曲线调整、暴雨强度公式拟合、精度检验、结果输出进行处理计算。
本文利用“年最大值法”对嵊泗国家基准气候站1980—2015年降水资料进行选样,并采用P-Ⅲ型分布曲线、指数分布曲线和耿贝尔分布曲线对11个降水历时分别进行拟合,得出P-i-t表(见表3)。

表3 嵊泗站3种曲线拟合P-i-t表

续表3
5 暴雨强度公式推求
不同拟合方法对应于不同的适应情况,本文主要进行暴雨强度总公式拟合、单一重现期暴雨强度公式拟合和区间参数公式拟合3种拟合,再通过对暴雨强度计算结果进行精度检验,误差越小、精度越高,最终确定嵊泗县暴雨强度公式。
5.1 暴雨强度总公式拟合
依据GB 50014—2006《室外排水设计规范》,暴雨强度公式的定义为:

式中:q为暴雨强度,L/(S · hm2);P为重现期,a;t为降雨历时,min;A1雨力参数;C为雨力变动参数;b为降雨历时修正参数;n为暴雨衰减指数。重现期越长、历时越短,暴雨强度就越大。
本文分别对P-Ⅲ型、指数分布、耿贝尔分布3种频率曲线,采用最小二乘法和高斯牛顿法进行暴雨强度总公式拟合,拟合结果见表4。

表4 嵊泗县暴雨强度总公式参数表
5.2 单一重现期暴雨强度公式拟合
从公式(3)可以得出,暴雨强度公式为已知关系式的超定非线性方程,公式中有4个参数,常规方法无法求解,因此参数估计方法设计和减少估算误差尤为关键。首先对式(3)进行线性化处理,即:

将公式(4)两边取对数,并令q=1nq,b0=1n167A,b=-n,x=1n(t+b),即转化成:

式(5)应用数值逼近和最小二乘法,求得b0及b1。将b值在(0,50)范围内取值,步长0.001,应用最小二乘法,求解A,n值。代入式(4)中,计算出q′′,同时计算出的降雨强度q′和计算的暴雨强度q′′的平均绝对方差σ,采用数值逼近法选取σ最小的一组A、b、n,从而推算出单一重现期暴雨强度公式[10]。本文选用精度最好的耿贝尔曲线拟合单一重现期暴雨强度,拟合结果见表5。

表5 嵊泗县耿贝尔分布曲线拟合单一重现期暴雨强度公式表

续表5
5.3 区间参数公式拟合
由于上文求得的单一重现期的暴雨强度公式,2个单一重现期之间的暴雨强度还无法求得,因此引入重现期区间参数公式,用以求解2个单一重现期之间的暴雨强度。
经反复推算和筛选,用公式y=b1+b21n(P+C)作为区间参数公式来求算区间参数值效果最佳(式中:y为A、b、n参数中的任一个;P为重现期;C为常数)。首先把1~100 a分为1~10 a和10~100 a 两个区间,将A、b、n分别代入公式y=b1+b21n(P+C)求解。同理,利用单一重现期暴雨强度拟合方法和最小二乘法分别求得2个区间下的A、b、n值,将得到的结果带入式(4)中,即可算出1~100 a的任意一个重现期暴雨强度公式。区间参数公式各参数值拟合结果见表6。

表6 嵊泗站暴雨强度区间参数公式各参数值拟合结果表
5.4 精度检验
5.4.1 检验方法与标准
为确保计算结果的准确性,对暴雨强度计算结果进行精度检验,计算重现期 2~20 a的暴雨强度,并将算得的暴雨强度理论值和实测值的平均绝对均方误差和平均相对均方误差,与GB 50014—2006《室外排水设计规范》(2014年版)规定的精度对照。规范中明确规定一般降水强度地区,平均绝对均方误差不超过0.05 mm/min;降水强度较强地区,平均相对均方误差不大于5%[7]。
平均绝对均方误差:

平均相对均方误差:
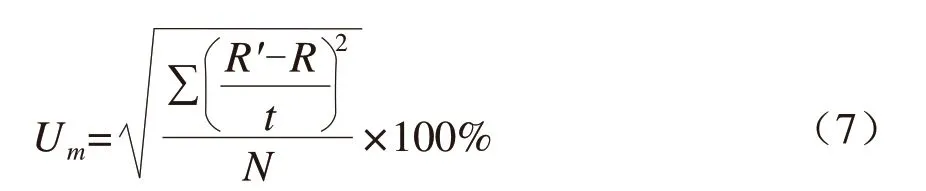
式(6)和式(7)中:R′为暴雨强度公式计算值,即理论降水量(mm);R为降水强度,即实际降水量(mm);t为降水历时(min);N为样本数。
5.4.2 确定最优拟合方案
利用嵊泗县气象站雨量资料,采用“年最大值法”选样方法,拟合得到暴雨强度总公式和区间公式。将5,10,15,20,30,45,60,90,120,150,180 min共计11个降水强度的实际观测值与用总公式及区间公式计算所得理论值之间进行检验,检验结果见表7。

表7 嵊泗县暴雨强度公式精度检验表
从总公式的拟合精度看,利用最小二乘法对耿贝尔分布曲线拟合出的总公式,平均绝对标准差和平均相对标准差均为拟合出的总公式中最小,即最优拟合结果。从区间公式的拟合精度看,基于耿贝尔分布曲线和指数分布曲线利用最小二乘法拟合出的区间公式平均绝对标准差一致,但是基于耿贝尔分布曲线利用最小二乘法拟合出的区间公式平均相对标准差更小,因此基于耿贝尔分布曲线利用最小二乘法拟合出的区间公式精度更高。综上,基于耿贝尔分布曲线利用最小二乘法拟合出的总公式和区间公式均为总公式和区间公式中最优结果。
从总体检验结果来看,除采用最小二乘法对P-Ⅲ型频率分布曲线拟合的区间公式拟合结果不符合GB 50014—2006《室外排水设计规范》(2014年版)要求外,整体上区间公式精度优于总公式拟合精度,并且基于耿贝尔分布曲线利用最小二乘法拟合出的区间公式为所有公式中最优拟合公式。
5.4.3 拟合结果检验
从暴雨强度公式拟合结果可以看出,暴雨强度区间公式精度稍高,但考虑规划设计部门使用暴雨强度公式时一般使用总公式,因此本文对精度较高的总公式均进行对比分析。
通过对嵊泗县暴雨强度总公式精度的对比分析,可见P-Ⅲ型最小二乘法、指数分布最小二乘法、指数分布高斯牛顿法、耿贝尔分布最小二乘法、耿贝尔分布高斯牛顿法暴雨总公式的拟合效果均符合规范要求,故将5种拟合方法进行对比,选取最优拟合方法作为嵊泗县的暴雨强度公式。
分别选取固定重现期P=2 a,P=3 a两种方案对5个暴雨强度总公式进行比较(见图1)。由图1 可知,5个暴雨强度公式算得的结果相差很小,因此从拟合结果考虑,基于耿贝尔分布曲线,利用最小二乘法拟合出总公式平均绝对标准差和平均相对标准差均最小,拟合效果最好,因此选取耿贝尔分布最小二乘法总公式作为嵊泗县暴雨强度公式。
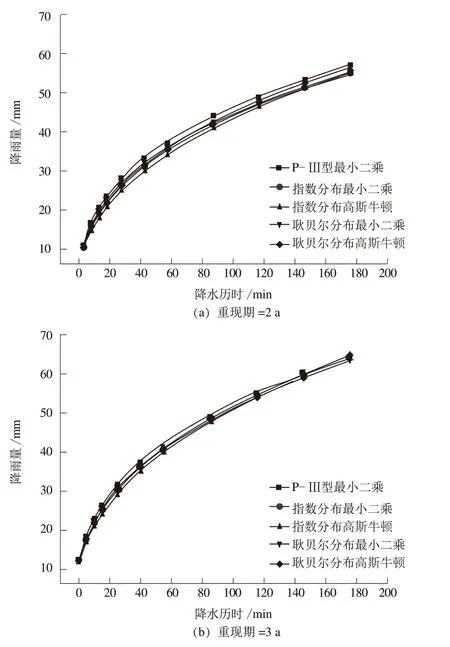
图1 暴雨强度公式降雨量计算结果比较图
6 结 论
(1)总结1980—2015年共36 a期间嵊泗县短历时降雨量年际变化特征,强降水事件发生频率变化不大,较为平稳,30 min以下短历时极端降水量呈下降趋势,但30 min以上(除120 min外)累计降水量呈增加趋势。
(2)根据嵊泗国家基准气候站1980—2015年共36 a降水量资料,采用“年最大值法”,选取每年5,10,15,20,30,45,60,90,120,150,180 min共11个降水历时的年最大值作为建立暴雨强度公式的统计样本,重现期采用1,2,3,5,10,20,50,100 a等8个期限,拟合暴雨强度总公式、单一重现期暴雨强度公式以及区间参数公式。结果表明:除采用最小二乘法对P-Ⅲ型频率分布曲线拟合的区间公式拟合精度不符合规范要求外,其余拟合结果均符合规范要求,总体上区间公式精度优于总公式拟合精度,其中基于耿贝尔分布曲线利用最小二乘法拟合出的总公式和区间公式均为总公式和区间公式中最优结果,并且拟合出的区间公式为所有公式中最优拟合公式。
(3)考虑规划设计部门使用暴雨强度公式时一般使用总公式,经检验,最终确定基于耿贝尔分布曲线,利用最小二乘法拟合出总公式为嵊泗县暴雨强度最终公式:


