基于多机载预警雷达的机动目标融合跟踪方法

戴 瑜，龙文佳

（湖北大学知行学院，武汉 430019）

0 引言

多机载预警雷达通过协同探测，可以实现对机动目标的精确跟踪，获得目标的状态及属性信息，形成完整的战场态势，夺取现代战争的制信息权［1］。

机动目标的跟踪是多机载预警雷达数据融合研究中的一个难点，当前，对机动目标的跟踪采用的主要方法为基于卡尔曼滤波的BLUE 算法和IMMPDAwoOoSM 算法［2-6］。然而，由于目标运动状态和杂波环境的复杂性，使得传统的卡尔曼滤波本身不足以完全解决该问题。为此，本文基于量测噪声协方差估计设计了一种优化了的卡尔曼滤波器［7-8］，引入了协方差交集的概念，提出了一种针对多机载预警雷达数据融合中机动目标跟踪的新方法。相比现有的方法，该方法具有更高的跟踪精度。

1 基于量测噪声协方差估计的优化卡尔曼滤波器设计

假设在一般情况下，对于以恒定速度直线运动的目标而言，目标速度的加速度符合高斯白噪声特性，则可以对卡尔曼滤波器进行以下优化和调整［9-10］。目标的状态方程模型可以表示为

其对应的噪声协方差表示为

该协方差矩阵通常表现为高斯白噪声协方差矩阵，现在考虑状态矩阵的构建

从式（6）可以看出，加速度矢量被认为是一种状态噪声，可以通过Fk矩阵进行状态估算。于是修改的协方差表示为

以上优化过程，仅对目标以恒定速度直线运动时的优化有效。如果目标方向发生机动或改变，则以上估计器的过程噪声将增加，而且这种噪声也不再是高斯白噪声，但可以合理地将其视为测量噪声。

实际测量向量与估计向量之间的误差为

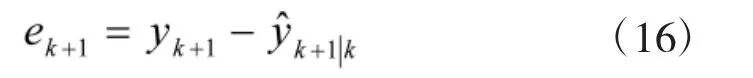
基于式（10），同时考虑引入的测量噪声，则上式可表示为

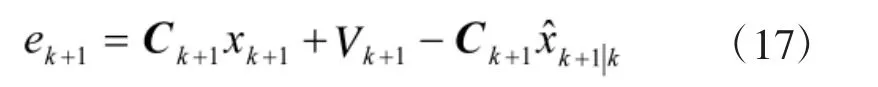
进而，由式（17）可以得到测量噪声Vk+1的表达式

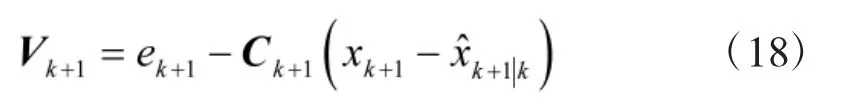
则该测量噪声向量的协方差及其协方差矩阵Rk+1为

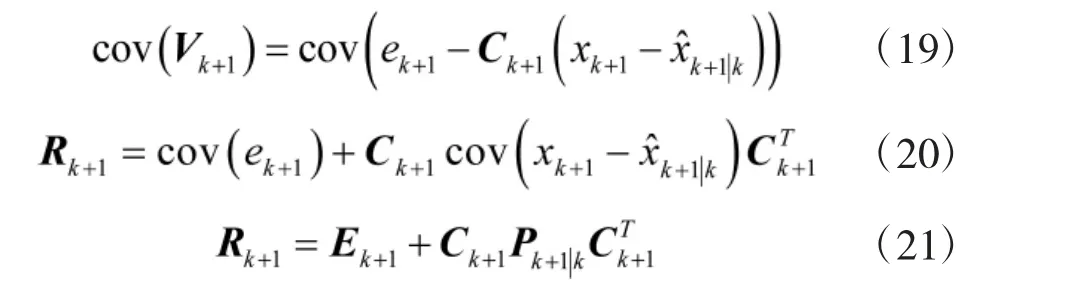
测量误差协方差的估算可以由滑动平均滤波器实现

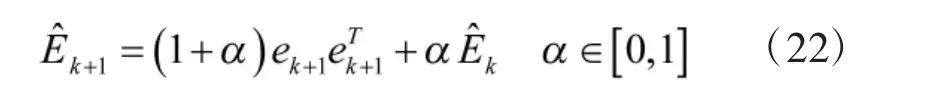
该滤波器具有统一的稳态增益，并且α 可以用滑动平均滤波器的点数n 表示为

可以重新排列，由α 找到所需的滑动平均滤波器的点数n 如下

其中，α 的值可以通过模糊逻辑方法给出最佳估计。

在检测概率较高的情况下，由式（16）可知，强机动目标会使真实测量值与测量的预测值间的偏差变大，使式（22）所表征的不确定性增大，进而进一步使式（21）所表征的测量方差增大。根据式（13）可得，测量不确定性的增加使得滤波增益减小，从而在状态更新中对滤波值的计算更依赖于状态的预测，而不是最新的测量信息，此时匀速直线运动模型的设定便限制了对机动目标的跟踪性能。但是，在本文方法中，采用了滑动平均滤波对信息协方差进行估计，通过滤波系数的自适应更新，能够有效调整信息不确定性的大小，对机动目标给出更大的滤波增益，以此提高对机动目标的跟踪新能。

2 滑动平均滤波器参数的估计

由式（24）可知，估计出α 的值就能确定合适的滑动平均滤波器的采样点数n。本文采用Bellman和Zadeh 提出的模糊逻辑理论［11］，用于优化测量协方差的Fresenius 范数方差，这种方法确保了模糊目标函数和模糊约束都有同样的约束条件。具体约束条件如下：

1）当目标发生转向机动，噪声是非高斯，需要最小化Frobenius 测量协方差。

2）重构前提是系统中噪声通过小的加速条件产生。

对于测量噪声协方差矩阵的估计Frobenius 范数的平均值，可表示如下

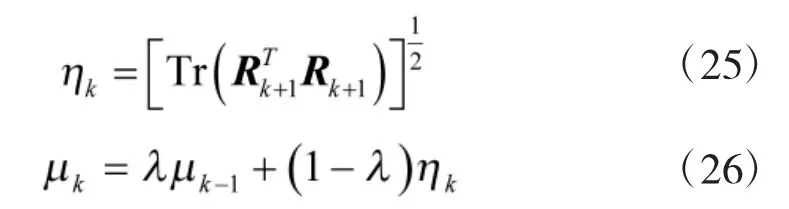
则模糊隶属方程和精确递归方差由下式给出

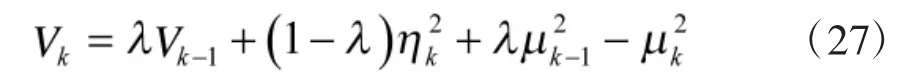
上式可以近似为

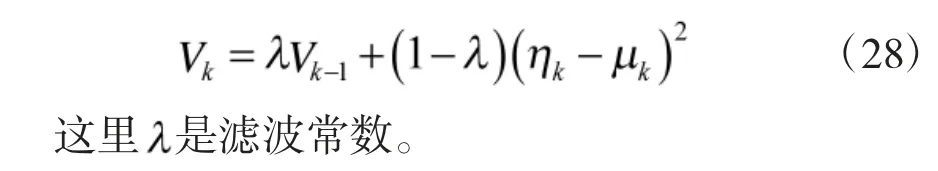
在每次迭代时，将对比当次Vk与前面最大Vmax值，如果Vk＞Vmax，则Vk用代替Vmax。然后模糊隶属函数横坐标刻度确定为

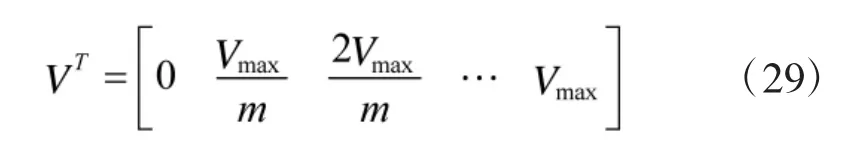
该集合将方差模糊化为隶属度。这实际上是将模糊化与基于规则的模糊推理相结合的模糊推理。这样，通过去模糊化处理，给出了优化的滤波系数

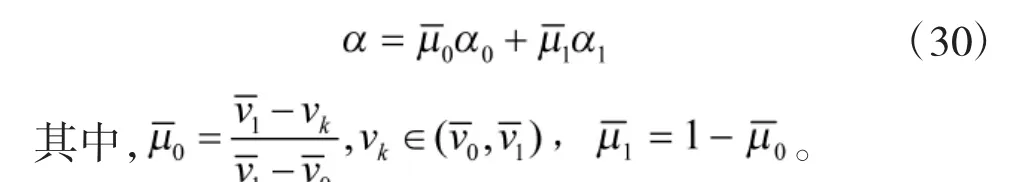
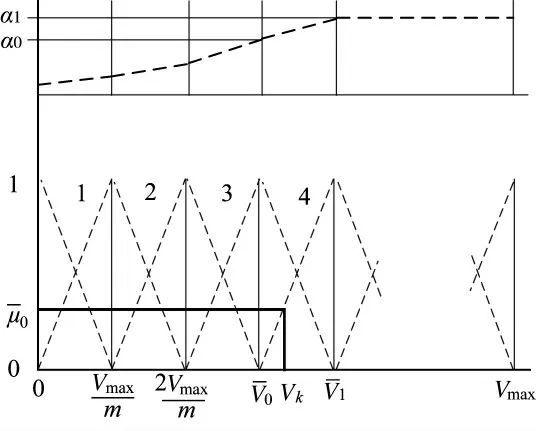
图1 模糊推理隶属函数值

图1 给出模糊推理隶属函数值的示意图。这种简单的线性组合产生可接受的性能，但需要进一步研究来调整α 和隶属函数横坐标。

3 多机载预警雷达数据融合

多机载预警雷达协同探测时，需要将多组跟踪信息融合在一起，以产生一致的态势感知，即协方差交集［12］。协方差交集采用在信息空间中表示的平均和协方差估计的凸组合［13-15］。在这种意义上，这种凸组合是一致的，即所得到的协方差超椭圆体包含在每单个估计器的所有协方差超椭圆体的外界。

下面给出了基于两传感器信息交集的一致协方差和平均估计值μ∈［0，1］

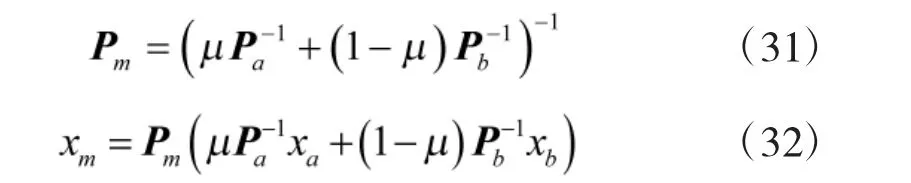
对于n 部传感器交集，可以应用一般均匀加权方案，随着更多信息可用及接收到的数据可靠性变化而可以相应变化。下面给出具体实现方法：

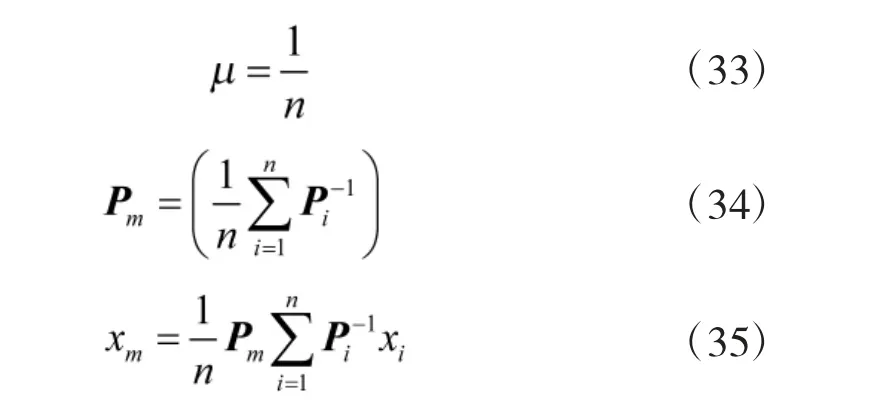
4 仿真分析

为了验证本文方法的有效性，首先设置了具有一个目标和两个机载预警雷达传感器平台的仿真环境，如图2 所示。两个雷达传感器的飞行平台分别在5 000 m 的高度以150 m/s 和100 m/s 的速度巡航。运动目标在1 000 m 高度，以200 m/s 的速度巡航。

仿真中，高斯白噪声被传入位置和角度零均值和方差测量分别为30 m/s2和0.1 mrd。当采纳简单卡尔曼滤波方法，这些噪声的传入会导致在非线性目标估计器中产生相当大的误差。

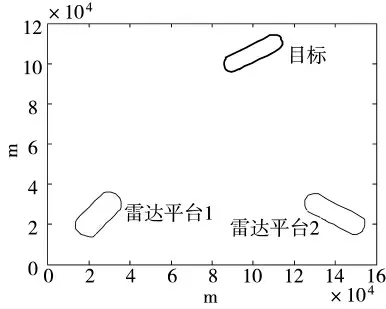
图2 机载预警雷达和目标的几何位置关系图

图3（a）给出了目标所在区域内的飞行路线，为椭圆形跑道，图3（b）给出了非直线段的实际航行的速度值。图4 给出了基于常规卡尔曼滤波的目标航迹融合和跟踪结果，可以看出，融合的位置和速度值误差较大，融合航迹起伏较大，不平稳。图5 给出了基于本文算法的融合结果，可以看出目标的位置和速度估算误差小，速度误差减小了一个数量级，使其成为位置预测的可用度量，融合航迹平滑且接近真实航迹。该算法能够优化模糊逻辑反馈控制滑动平均滤波恒定递归地测量方差，并允许系统不断适应任何性质的噪声改变，重新计算状态协方差矩阵和估计测量噪声协方差矩阵。

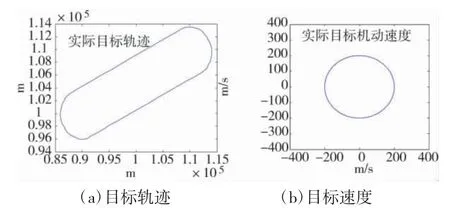
图3 目标的实际位置和速度

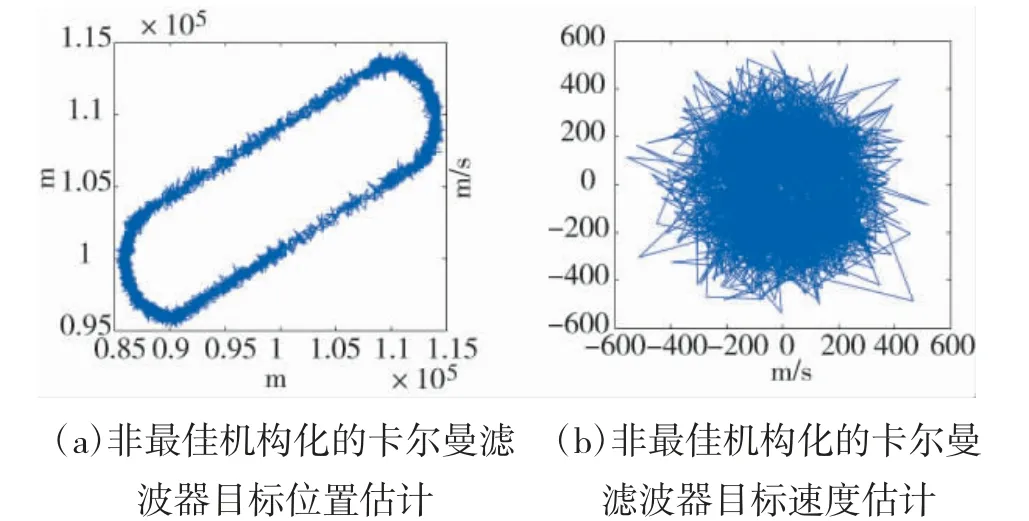
图4 基于常规卡尔曼滤波的目标航迹跟踪结果

图5 基于本文算法的目标航迹跟踪结果

假设目标机动飞行，目标的起始位置为（120.8°E，40.1°N），飞行过程中高度始终为6 000 m，航线上有两个机动拐弯点，分别是（119.9°E，39.9°N）和（120.3°E，40.2°N），拐弯点之间目标直线飞行，目标的机动转弯采用常速率转弯模型进行描述。

仿真中，设置两部预警机，预警机航线均为直线飞行，两者的速度均为250 m/s。其中，第1 部预警机在（118.7°E，40.2°N）和（120.2°E，40.2°N）之间匀速飞行，高度6 040 m；预警机2 在（118.7°E，39.8°N）和（120.2°E，39.8°N）之间飞行，高度6 000 m。

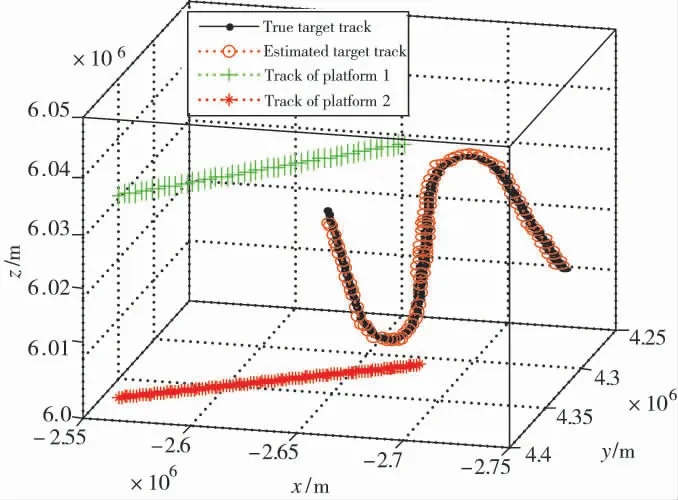
图6 基于本文算法的融合仿真结果

图6 给出了基于本文提出算法的目标跟踪结果。从图中可直观看出，本文提出的算法成功稳定地跟踪机动的运动目标。图7 给出了300 次蒙特卡洛实验的位置和速度均方根误差（RMSE）性能比较结果，其中，包含BLUE 算法、IMMPDAwoOoSM 算法（“乱序”目标中未利用OoSM 测量的IMMPDA 算法）［3］，结果表明本文算法的误差性能是最佳的。需要指出的是，每次仿真中均对目标和机载雷达的初始位置、初始速度加入一定的随机扰动以模拟实际场景中的不确定性，再加上起始时刻滤波器尚未收敛，滤波误差相对较大，因此，造成起始误差的不同。

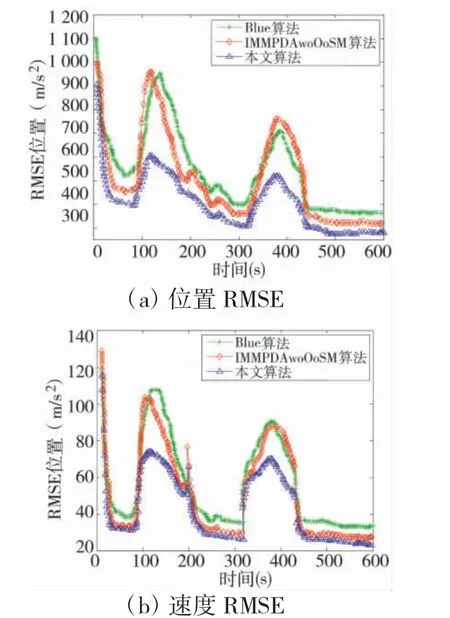
图7 跟踪性能比较

5 结论

针对多机载预警雷达信息融合中的机动目标跟踪问题，本文从转换量测Kalman 滤波角度，提出了一种多机载预警雷达平台跟踪机动目标的新方法。该方法通过噪声源进行重组，简化噪声协方差模型状态，从优化单系数滑动平均滤波器来估算测量噪声协方差，通过基于优化模糊逻辑，使利用协方差矩阵估算测量的罗伯尼范数方差最小化，仿真分析表明，该方法能够较好解决多机载预警雷达数据融合中的机动目标跟踪问题。