基于电力电子变压器的串联型12脉波整流器

孟凡刚， 姜彤， 郭依宁

(哈尔滨工业大学(威海) 新能源学院，山东 威海 264209)

0 引 言

多脉波整流技术具有结构简单、实现难度低、可靠性高等优点，适应于大功率整流系统[1]。根据后级三相二极管整流桥连接方式的不同，多脉波整流器可分为串联型多脉波整流器和并联型多脉波整流器两种。相比较而言，串联型多脉波整流器输出电压加倍，且具有更好的平衡性，被广泛应用于蓄电池充电和高压直流输电等高压大功率场合[2-3]。移相变压器是串联型多脉波整流器的必需器件，其主要作用是提供几组存在相位差的三相交流电压，给后级的几组三相二极管整流桥供电。但是，传统工频移相变压器体积大、质量重，不仅增加了多脉波整流器的安装和运输难度，还占用了较大的空间，限制了串联型多脉波整流技术的应用。

为解决传统工频移相变压器体积大质量重的问题，文献[4-6]提出了使用自耦变压器代替传统工频移相变压器的方法，但是，自耦变压器本身就存在安全性低、绕组结构复杂、仅适用于非隔离场合等缺点[7]，且受整流器结构的影响，使用自耦变压器的方法对并联型多脉波整流器有效，对串联型多脉波整流器不适应，目前尚未发现与此相关的研究内容。文献[8-10]提出使用电力电子变压器代替传统工频移相变压器的方法，但是，这些文献未提到使用电力电子变压器代替传统工频移相变压器后三相二极管整流桥导通模态的变化以及整流器的工作特性。将电力电子变压器技术与多脉波整流技术相结合，为提高多脉波整流器性能提供了一种新的思路[11-12]。

本文对基于电力电子变压器的串联型12脉波整流器进行了研究，使用电力电子变压器代替传统工频移相变压器，达到减小移相变压器体积与重量、提高其功率密度的目的。所研究的整流器具有输出电压加倍、平衡性好、控制电路简单、功率密度高等优点，主要适应于空间有限或承重有限的高压大功率电能变换场所。实际电路中，为提高整流器输入电压的承受能力，电力电子变换器采用高耐压等级的电力电子器件，电力电子变换器可采用多模块化结构。

1 基于电力电子变压器的串联型12脉波整流器的电压分析

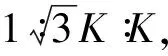
为了便于分析基于电力电子变压器的12脉波整流器，做以下假设：

1)三相交流输入电源为理想电源；

2)所以开关器件均为理想开关器件；

假设整流器的三相交流输入电压为：

(1)

其中Us为输入电压的幅值。

本文仅对基于电力电子变压器的串联型12脉波整流器的a相进行分析，b相和c相的分析原理与a相分析原理相同。根据高频变压器的联结结构和匝比关系，结合图1和图2，可以得到电力电子变压器的输入电压uAn1和高频变压器副边电压uA2n2满足以下关系：

图1 基于电力电子变压器的串联型12脉波整流器Fig.1 A series-connected 12-pulse rectifier based on power electronic phase-shifting transformer

图2 高频变压器绕组结构图Fig.2 Winding configuration of high-frequency transformer

(2)

电力电子变换器的主要作用是将输入的低频交流电变换为高频交流电。图3所示为a相电力电子变换器的开关函数波形(以升频至500 Hz为例)。其中，Sadio为单相桥式不控整流电路的开关函数，Sak为单相全桥逆变电路的开关函数，Sw为整个电力电子变换器的开关函数。a相电力电子变换器的开关函数表达式可以表示为

图3 a相电力电子变换器的开关函数Fig.3 Switching function of power electronic converter

(3)

其中ωs为高频方波信号的角频率。

在平衡状态下，电压un2G可以表示为

(4)

根据图1、图2和式(4)，电压un2G和uA2n2可以表示为：

(5)

其中：uo为负载电压；uFP为点F和点P之间的电势差；Ud为二极管正向导通压降。

开关函数sgn(x)定义为

(6)

根据式(2)和式(5)可以得到电力电子变压器输入电压与高频变压器输出电压之间的关系，但式(5)中点F与点P之间的电势差uFP为未知量。为获得电力电子变压器输入电压的表达式，需求解电压uFP。下面利用开关函数法分析后级三相二极管整流桥的导通模态。

使用电力电子变压器代替工频移相变压器后，工作频率的升高导致整流器中两组串联连接的三相二极管整流桥的导通模态发生变化，与其工频状态下的导通模态有所差别。定义三相二极管整流桥桥臂的开关函数为Sx，x代表三相二极管整流桥桥臂的导通状态：当x>0时，代表的是整流桥桥臂的上桥臂导通；当x<0时，代表的是整流桥桥臂的下桥臂导通；当x=0时，代表的是该整流桥桥臂不导通。整流桥Rec2的导通模态如图4所示。主要特点有：在整流器运行的任意时刻，2个串联的三相二极管整流桥都有5个二极管处于导通状态；在一个周期内，每个管子导通的总角度为150°；由于工作频率的升高，三相二极管整流桥的上下桥臂处于高频交替导通状态；两组三相二极管整流桥的导通模态存在30°的相位差。

图4 整流桥Rec2的导通模态Fig.4 Conduction mode of Rec2

开关函数Sx可以表示为

(7)

根据图1和图4，可以得到基于电力电子变压器的串联型12脉波整流器共有12种工作模态，如表1所示。

当整流器工作于模态1时，因为高频切换的原因，又可对应到Sw=1和Sw=-1两种情况：第一种情况，当Sw=1，导通的二极管为D15D16D11D26D21；第二种情况，当Sw=-1，导通的二极管为D12D13D14D23D24，第二种工作情况与工作模态2重复，在这两种情况下，电压uFP表达式为

(8)

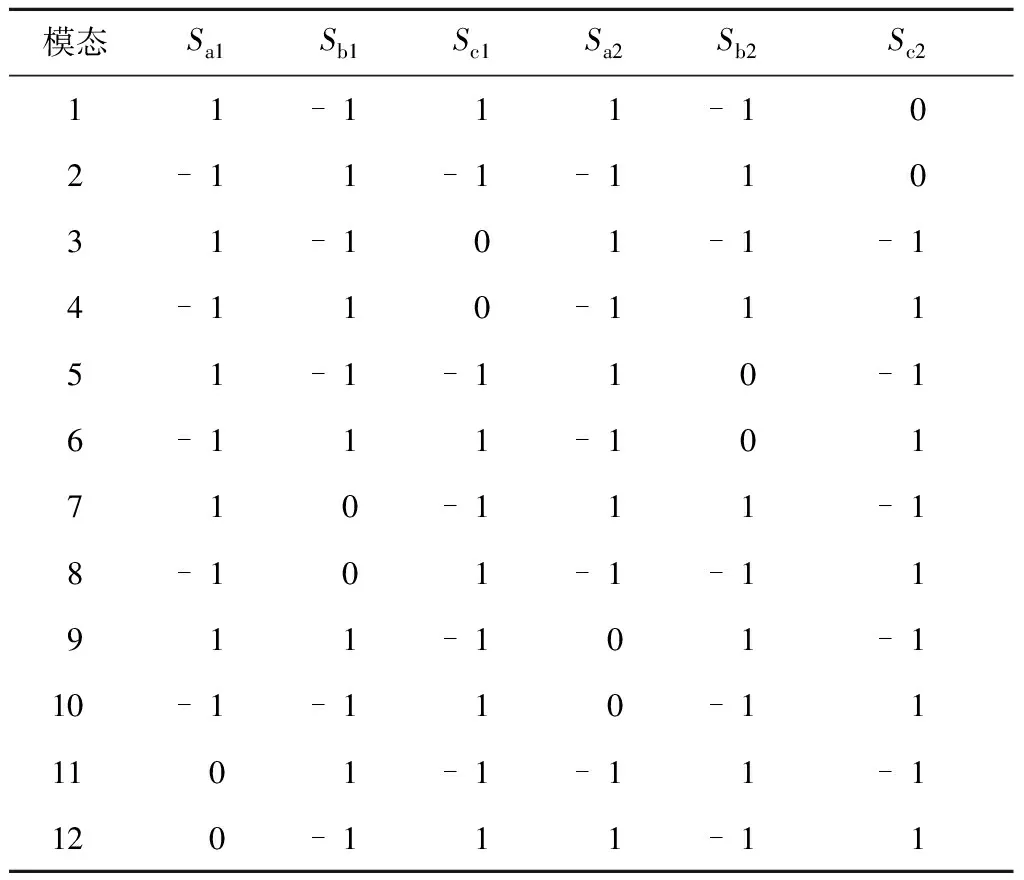
表1 整流器的12种工作模态

当整流器工作于模态3时，因为高频切换的原因，也可对应到对应到Sw=1和Sw=-1两种情况：第一种情况，当Sw=1,导通的二极管为D16D11D26D21D22，第二种情况，当Sw=-1，导通的二极管为D13D14D23D24D25，第二种工作情况与工作模态4重复，在这两种情况下，电压uFP表达式为

(9)

以同样的方式分析其余的10种工作模态，可以得到电压uFP的数值只有两种，是一个6倍频方波。电压uFP的数值如表2所示，设

根据式(2)、式(3)、式(5)、式(10)、表1和表2可以得到电力电子变压器的输入电压表达式为

(10)

表2 12种工作模态下电压uFP的数值

(11)

其中φ表示的是三相交流输入电压与电力电子变压器输入电压之间的相位差。

根据式(11)，使用MATLAB绘制电力电子变压器的输入电压波形，其为12阶梯波，如图5所示。

图5 电力电子变压器输入电压波形示意图Fig.5 Input voltage waveform of power electronic transformer

2 基于电力电子变压器的串联型12脉波整流器的电流分析

为求整流器输入电流的表达式，引入等效电阻的概念，每相电力电子变换器的右侧等效为电阻Re，建立整流器的解析模型如图6所示。

图6 整流器的解析模型Fig.6 Analytical model of the rectifier

电力电子变压器输入电压中谐波相较于基波来说小很多，为便于分析，用电压基波值来近似代替电压值，根据输入输出功率平衡，可以得到

(12)

由式(12)可知，在输入电压已经确定的情况下，等效电阻的取值只与负载有关。为简便起见，单独分析a相的电流。基于建立的整流器的解析模型，a相的输入电流可表示为

(13)

输入功率因数kp可表示为

(14)

根据解析模型，可以总结出在输入电压和负载确定情况下，输入功率因数与串联型12脉波整流器的电感参数的选取有关。假设Re/(ωLs)为x，根据式(14)，可以画出输入功率因数与x的关系如图7。

图7 输入功率因数kp与Re/(ωLs)的关系图Fig.7 Relationship between input power factor kp and Re/(ωLs)

根据图7可以看出，kp与Re/(ωLs)的选取有关。理论上，Re/(ωLs)的比值越大，输入功率因数将越接近于1；在负载和输入电压确定的情况下，Ls的取值越小，输入功率因数越大，但滤波能力会下降。

3 仿真与实验验证

为验证上述理论分析的正确性和有效性，本节设计了一个1 kW的实验样机，并进行了相应的仿真和实验验证。仿真和实验条件如下：1)输入相电压为120 V；2)输入电感Ls=10 mH；3)电力电子变换器将工频升频为500 Hz；4)高频变压器的绕组结构为Y/Δ/Y，匝比为1∶1.107∶0.639；5)大电容C1=C2=3 300 μF/450 V；6)负载电阻为130 Ω。

图8所示高频变压器与工频变压器的实物对比图。图中，左侧为额定工作频率50 Hz的工频变压器，其右侧为额定工作频率500 Hz的高频变压器。两种移相变压器均使用Z10铁芯材料制作，容量相等约为2 000 kVA。通过测量可得，传统工频移相变压器的体积约为高频变压器体积的3倍。表3为工频变压器与高频变压器的体积重量。

图8 相同容量的高频变压器和工频变压器的实物对比Fig.8 Physical comparison of high frequency transformers and power frequency transformers of the same capacity

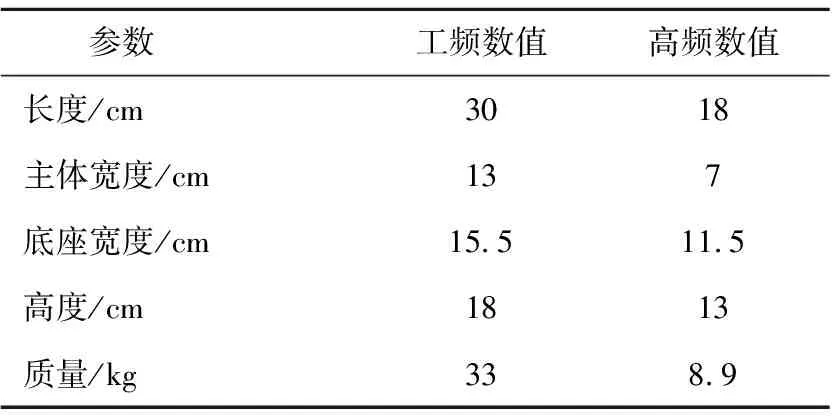
表3 工频变压器与高频变压器的体积重量

图9所示为基于电力电子变压器的串联型12脉波整流器实验装置图。其中，电力电子变换器和三相二极管整流桥均可模块化，使整流器结构更加紧凑。

图9 整流器的实验装置图Fig.9 Experimental setup of rectifier

图10所示为电力电子变压器的输入电压仿真与实验波形，可以看出其为12阶梯波，理论分析与仿真实验结果相符。THD的实验值约为10%。

图10 电力电子变压器的输入电压Fig.10 Input voltage of power electronic transformer

图11所示为整流器输入电流波形。输入电流由12段弧线组成，THD的实验值约为6.5%。

图11 整流器的输入电流Fig.11 Input current of rectifier

图12所示为电力电子变压器的输入电压经过电力电子变换器时，各变换过程的电压波形，12阶梯波经单相不控整流电路整流，后经过单项全桥逆变电路变换为500 Hz的高频交流电压。理论分析与仿真实验结果相符。

图12 电力电子变换器变换过程波形Fig.12 Transformation waveform of power electronic converter

图13所示为整流器负载电压uo和负载电流io的波形。阻性负载下，负载电压和负载电流的纹波均非常小。

图13 负载电压和负载电流Fig.13 Load voltage and load current

4 结 论

本文研究了一种基于电力电子变压器的串联型12脉波整流器，使用了电力电子变压器技术与多脉波整流技术相结合的方法，在保证串联型多脉波整流技术优势的前提下，减小了传统工频移相变压器的体积与重量，提高了其功率密度。仿真与实验结果表明，使用该方法后，高频变压器的体积约为同容量工频变压器体积的三分之一，功率密度显著提高，且整流器的电能质量能得到保证。本文主要研究的是12脉波整流器的情况，但方法可推广至其他类型的多脉波整流器中，拓宽了串联型多脉波整流技术的应用范围。