基于反步法的SCARA机器人轨迹跟踪控制

赵娜，吕成兴

(1.齐鲁工业大学(山东省科学院) 山东省海洋仪器仪表研究所 山东省海洋环境监测技术重点实验室 国家海洋监测设备工程技术研究中心，山东 青岛 266033；2. 青岛理工大学 信息与控制工程学院， 山东 青岛 266000)

选择顺应性装配机器手臂(selective compliance assembly robot arm，SCARA)机器人是典型的机械臂系统，其结构设计如图 1所示。由于具有结构简单等优点，目前已广泛应用于组装、焊接、加工等行业[1-5]。同时，这些领域对于SCARA机器人的运行速度和轨迹跟踪精度也提出了更高的要求。因此，研究SCARA机器人的轨迹跟踪问题在理论和实践中都具有极其重要的意义。

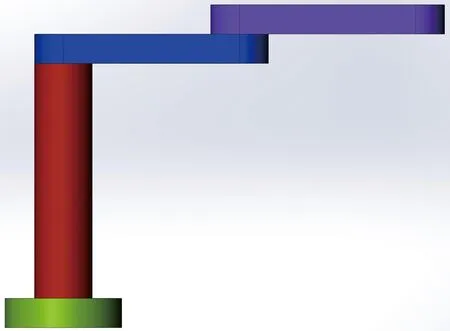
图1 SCARA机器人结构示意图Fig.1 Schematic of SCARA robot

由于机械臂系统是高度非线性的系统，因此线性控制的方法难以获取良好的动态和稳态性能。滑模控制的滑模面不受被控对象的参数不确定性和外部干扰的影响，因此经常在机械臂的控制中使用，然而滑模控制容易引入颤振现象[6-7]。模糊控制不需要建立精确的数学模型，但是其稳态性能并不理想[8]。反步设计方法对于非线性系统、尤其是带有不确定性的非线性系统具有较强的处理能力。Nikdel等[9]通过设计自适应反步控制器来提高机械臂的轨迹跟踪性能，控制器在模型非线性和参数不确定性的情况下保证了系统稳定性以及良好的跟踪性能。反步法相对于其他的渐近收敛算法，具有收敛速度快、控制精度高和抗干扰能力强等优点。目前SCARA机器人系统的时变轨迹跟踪问题依然存在控制精度不足、抗干扰能力较差等缺点。针对SCARA机器人系统时变轨迹跟踪的控制精度问题，本文提出了一种新型的反步法轨迹跟踪控制器，该控制器具有优良的动态与稳态性能，且能够快速消除误差。

1 机器人模型

二自由度机器人的动力学方程表示为：[10]

(1)

其中q∈2为机器人关节的角位移向量，2为机器人关节的角速度向量，2为机器人关节的角加速度向量。M(q)∈2x2为惯性矩阵且为正定，2x2为离心力和哥氏力向量，τ∈2为系统的输入力和力矩向量，τd∈2为扰动输入且假定其为有界的。

2 控制器设计

对于二自由度SCARA机器人的非线性运动学和动力学数学模型，忽略扰动项，采用反步法设计机器人的轨迹跟踪控制律。

选取系统的状态变量分别如下

(2)

则误差向量为

(3)

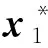
(4)

选取虚拟控制量为

(5)

沿系统的轨线，对V1微分，得

(6)

(7)

设计李雅普诺夫候选函数为：

(8)

(9)

(10)

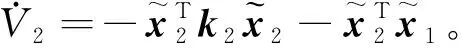
V=V1+V2。

(11)

3 仿真与讨论

为了验证所设计算法的有效性，我们进行了仿真实验。机器人模型参数为：

(12)

其中，控制器参数设计为：kp1=kp2=300，kd1=kd2=100。

我们设计两个应用场景来验证所设计控制器的有效性。场景一为给定期望轨迹信号为阶跃信号，场景二为给定期望信号为时变信号。q=[q1pd,q2pd]T为非线性PD轨迹跟踪控制器产生的轨迹信号，q=[q1,q2]T为所设计反步法控制器产生的轨迹信号。

3.1 阶跃信号轨迹跟踪仿真

关节1和关节2的期望位置信号q=[q1d,q2d]T为单位阶跃信号。由图 2可以看出，在极短的时间内关节1和关节2的位置跟踪到了期望信号，所设计的控制器的动态能性优于非线性PD控制器的动态能性。由图3可以看出，输入力矩为光滑曲线，所设计控制器的力矩曲线光滑合理。

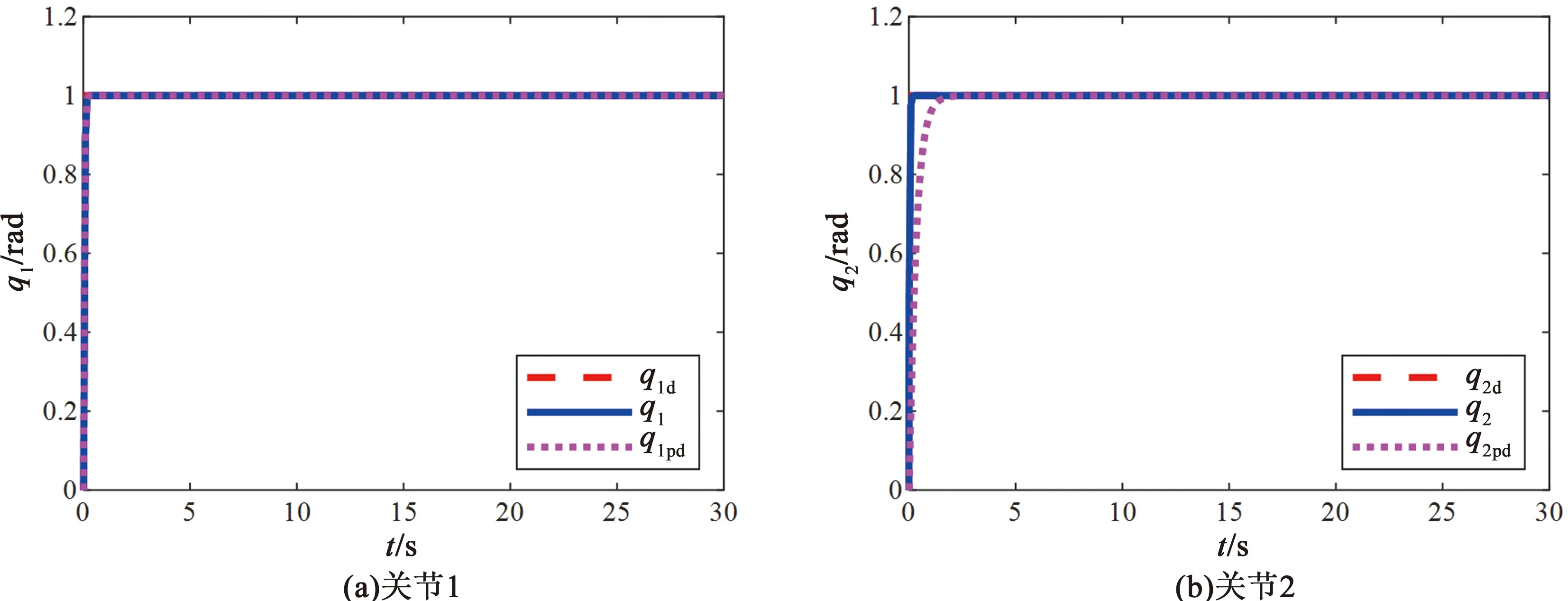
图2 关节阶跃信号轨迹跟踪仿真图Fig.2 Tracking position of joint step signal

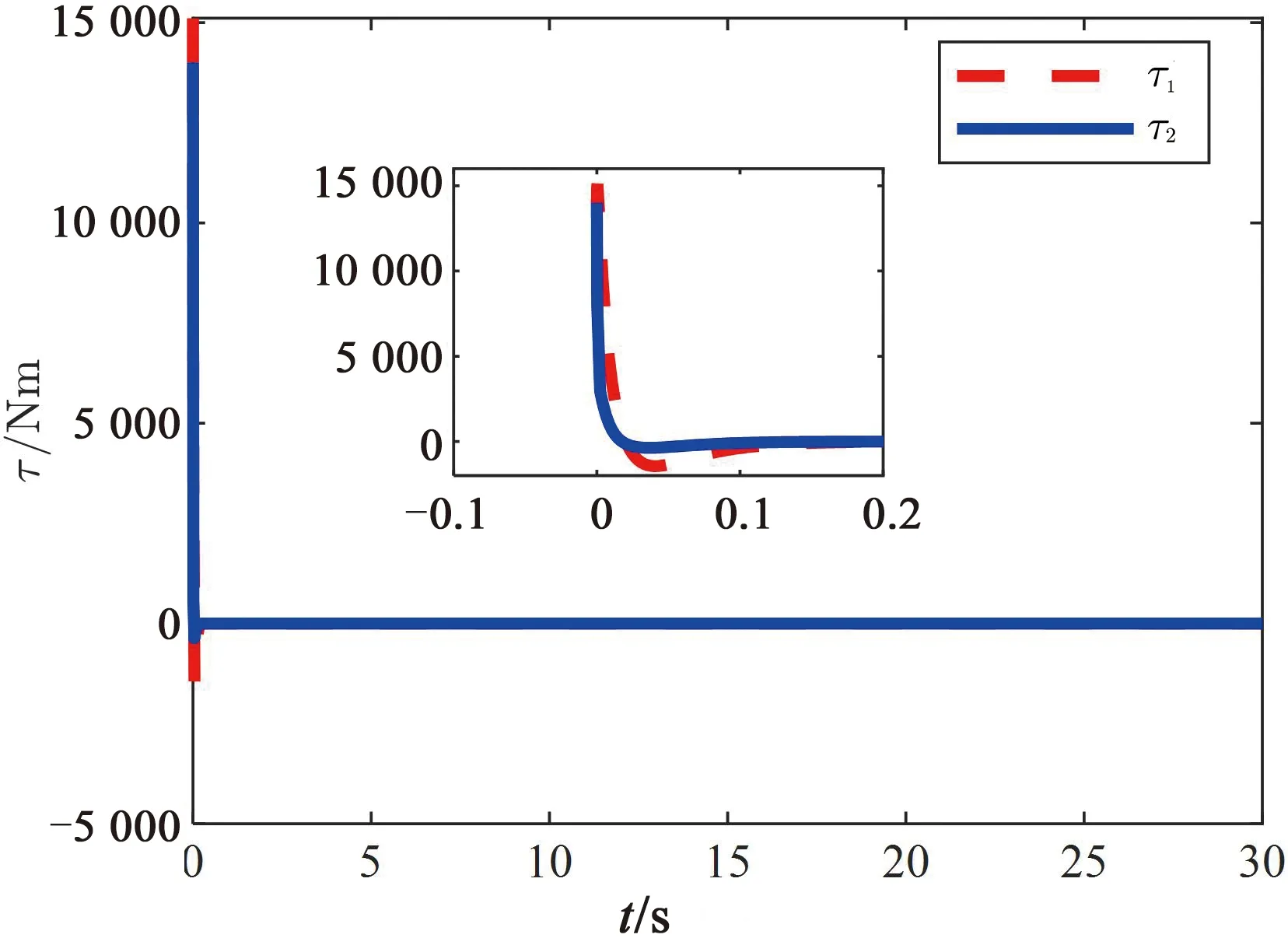
图3 阶跃信号的系统输入力矩Fig.3 Input torque of system under step signal

由图4可以看出，加入定值扰动τd=[5,5]T时，跟踪曲线有误差存在，而所设计的反步控制器动态性能和稳态性能均优于PD控制器。

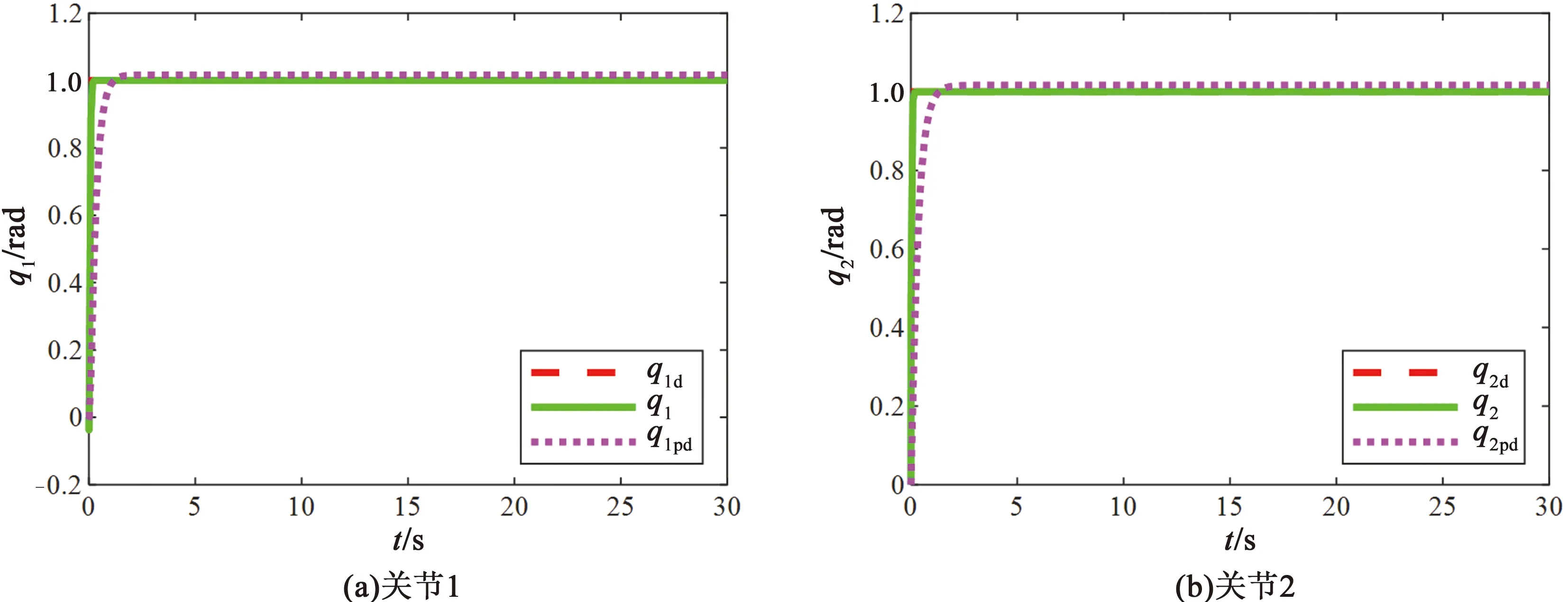
图4 加入扰动时关节阶跃信号轨迹跟踪仿真图Fig.4 Tracking position of joint with disturbance under step signal

3.2 连续时变信号轨迹跟踪仿真

设计期望时变轨迹信号为：q1d=2.5sin (0.2t) ，q2d=2.5cos (0.2t)。控制器参数设置不变。由图5可以看出，对于连续时变信号期望轨迹，所设计的控制器可以快速跟踪，并具有良好的稳态性能。由图6可以看出所设计控制器的力矩曲线光滑合理。

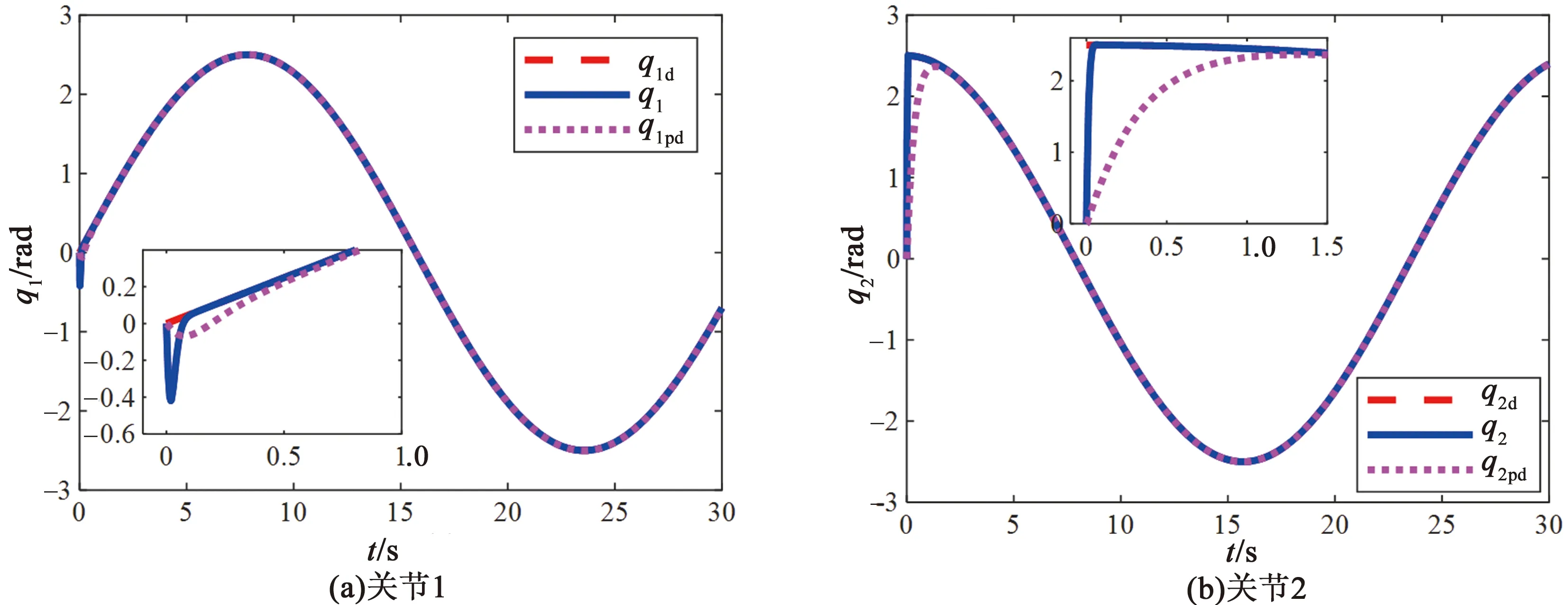
图5 关节时变信号轨迹跟踪仿真图Fig.5 Tracking position of joint under time-varying signal

图6 时变信号的系统输入力矩Fig.6 Input torque of system under time-varying signal

图7为关节1和关节2的位置跟踪曲线，可以看出，加入定值扰动τd=[5,5]T时，对于时变轨迹信号，PD控制器在有定值扰动存在时跟踪误差较大，而所设计的反步控制器动态性能和稳态性能均优于PD控制器。

图7 加入扰动时关节时变信号轨迹跟踪仿真图Fig.7 Tracking position of joint with disturbance under time-varying signal

4 结论

本文针对SCARA 机器人的时变轨迹跟踪问题，使用反步法设计了二自由度SCARA机器人的一种新型轨迹跟踪控制器。设计了闭环系统的李雅普诺夫函数，采用李雅普诺夫稳定性定理和拉萨尔不变集定理，证明了所设计的控制律保证二自由度机器人轨迹控制闭环系统是一致全局渐近稳定的。仿真结果表明，所提出的控制律对跟踪给定值信号和时变信号都取得了满意的控制效果，验证了控制律的有效性。在进一步的研究工作中，将解决轨迹跟踪控制中的不确定干扰问题。