大旋比V形带轮旋压三维成形仿真与验证

秦 飞 周 敏 王武荣 韦习成 唐季平 曹 进

(1.上海大学材料科学与工程学院, 上海 200444； 2.南通福乐达汽车配件有限公司, 江苏 南通 226000)

旋压是近代发展起来综合铸造、挤压、拉伸、弯曲、环轧和横轧等工艺特点的无切削加工的先进金属塑形成形工艺[1],也是一种通过旋转将力从点传递到线和面，并赋予力一定的方向，使加工过程中的金属件沿受力方向均匀变形的先进工艺。旋压成形工艺主要是利用金属材料的塑性变形和流动变形性能加工零件，采用旋压工艺生产V形带轮不仅可以避免机加工工艺所产生的缺陷和材料利用率低等问题，而且能保证加工件具有很高的强度和同轴度。

随着旋压工艺的广泛应用及旋压件形体的复杂化，数值模拟逐渐成为研究零件成形参数的主要手段。众多学者对旋压工艺开展了相关研究。Lossen等[2]提出了一种结合金属旋压和摩擦特性的新工艺用于加工管材，利用摩擦实现自感应生热对材料进行热处理，扩展了旋压时材料的成形极限。Jin等[3]提出了一种对圆盘状坯料边缘进行增厚的旋压加工工艺，并基于有限元模拟和正交试验，分析了成形过程中的主要缺陷和部分工艺参数对成形的影响。Ahmed等[4]提出了一种采用辊套和恒定间隙的毛坯保持器的新旋压工艺，解决了杯形件由于法兰起皱而导致的低成形性，抑制了变形起皱现象。Jin等[5]提出了用于加厚圆盘状边缘的五步旋压法，通过有限元模拟研究了圆盘状截面形状和流线分布，结果表明成形零件横截面的流线沿零件的形状分布。万里翔等[6]建立了多楔带轮旋压成形二维仿真模型，解决了齿面凹坑缺陷，并分析了每道次金属流动规律。唐季平等[7]使用Simufact有限元软件建立了齿形带轮旋压增厚模型，分析了旋压增厚过程中零件上耳部内侧过渡区材料折叠问题，并总结了变形区材料流动规律和折叠缺陷产生的原因。李萍等[8]基于Simufact有限元软件采用多道次旋压成形工艺的建模方法，解决了带横向外凸筋的齿形带轮凸筋部位难成形的问题。然而，目前对旋压工艺的研究大都集中于管材类、棒材类、杯形件和圆盘(碟形)类零件，少数对V形带轮的研究集中于2D模拟或不完全使用旋压工艺加工。但无论是对棒材、杯形件、管形件还是圆盘(碟形)状旋压件的研究，与V形带轮旋压成形相比，其成形机制都相对简单。V形带轮旋压成形区域小而变形量大，坯料与旋轮接触处应力应变分布不均匀，材料局部呈非稳态变形，在模拟过程中,坯料易局部破裂或局部区域材料堆叠，使刻齿仿真难以实现高精度模拟仿真成形[9]。目前对此类成形机制复杂的旋压件的研究还相对较少。因此，建立兼顾计算效率与模拟精度的V形带轮旋压仿真建模方案对旋压工艺调试与成形过程中缺陷的避免具有重要意义。

本文基于对V形带轮旋压成形特征的分析，借助Deform- 3D有限元软件建立了V形带轮旋压成形的有限元模型，并基于模拟结果分析了成形过程中的应力应变场分布，确保零件齿成形区域不破裂，并根据模拟结果试制零件。该研究结果可用于指导V形带轮的实际生产及同类型产品的开发。

1 V形带轮旋压工艺

1.1 材料参数

有限元模拟采用SPHE深冲用热轧软钢板(国产钢号08AL)，原始坯料厚度6 mm。材料基本性能参数：屈服强度215.6 MPa，抗拉强度335.7 MPa，断后伸长率45.3%，工程应力- 工程应变曲线如图1所示。

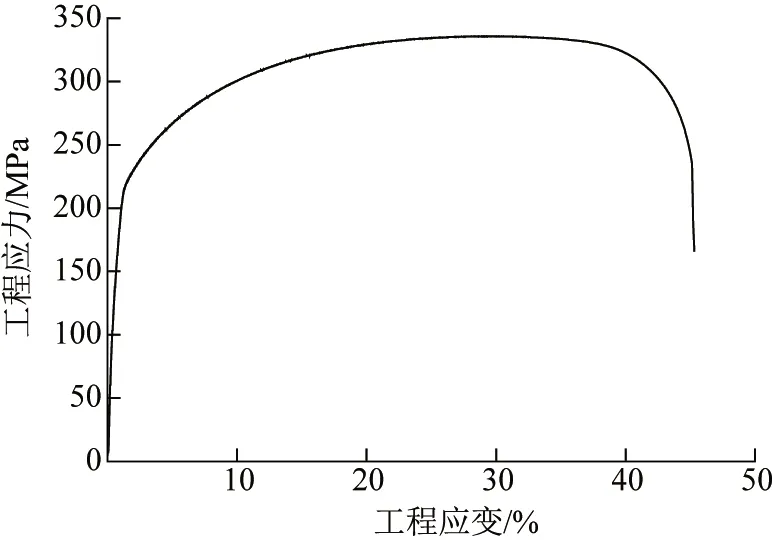
图1 SPHE钢的工程应力- 工程应变曲线Fig.1 Engineering stress- engineering strain curve of SPHE steel

在旋压过程中，由于受三向应力作用，SPHE钢的应变远高于其单向拉伸的颈缩应变。其变形过程为弹塑性变形，真应力- 真应变曲线见图2。

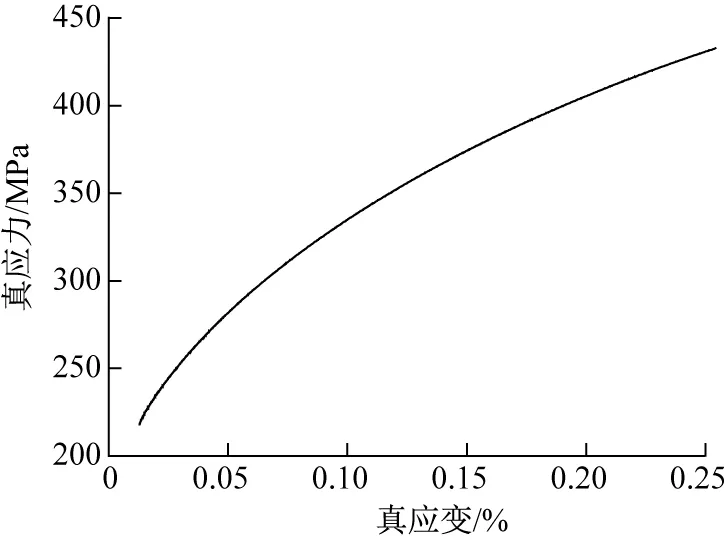
图2 SPHE钢旋压过程中的真应力- 真应变曲线Fig.2 True stress- true strain curve of SPHE steel during spinning

1.2 V形带轮结构

V形带轮为空心回转体零件，特点是整体尺寸大而齿形尺寸小且精度要求高，其剖面及齿形见图3。其中，齿尖圆弧半径约为零件直径的1/187，齿底圆弧半径约为零件直径的1/158，齿槽深度约为零件直径的1/21，齿间距约为零件高度的1/10。大旋比旋压是多因素耦合作用下的多道次局部加载和卸载的复杂过程，成形过程中易出现局部损伤破裂、隆起等[10]，因此复杂度极高。

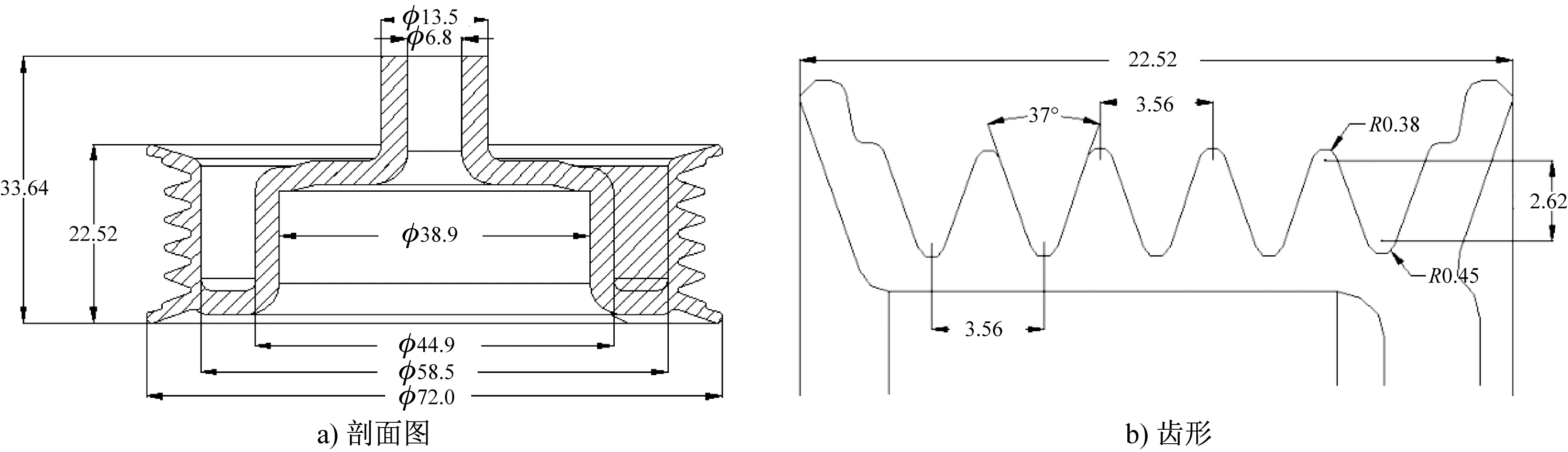
图3 V形带轮结构图Fig.3 Structure drawing of V- shaped belt wheel

1.3 工艺建模方案

V形带轮板料经冲压成圆盘状坯料，后经翻边成形内外筒壁而成零件毛坯。在后续旋压成形过程中，安装于旋压机的上模和下模具将零件毛坯Z向夹紧并自转，布置于X-Y平面内的多道次旋轮依次径向进给加压于零件毛坯外缘的坯料，使之产生局部塑性刻齿变形并最终成形为多楔带轮零件。根据多楔带轮旋压成形工艺流程提出了如下建模方案：通过螺旋进给替代传统建模方法，将坯料的自转转化为旋轮绕静止坯料的阿基米德螺旋进给运动，并设置黏着接触点使模型处于稳定状态。即坯料在模具夹持下固定不动，每一道次旋轮先从径向匀速靠近坯料，靠至即将接触坯料时，旋轮以坯料轴线为旋转中心做螺旋进给运动，进给到所需深度后以恒定半径绕坯料公转一圈，然后退出，每一道次旋轮本身不自转。

2 有限元模型建立及分析

2.1 建模过程

利用Deform- 3D软件模拟V形带轮的旋压成形过程，建立如图4所示的有限元模型。旋压模拟工艺参数如表1所示。建立自定义材料属性并赋予坯料，材料属性按1.1节所述进行定义。为了提高成形零件齿形的清晰度和模拟的精确度，模拟中做如下替换和简化。(1)坯料为弹塑性体，模具为刚性体。(2)由于六面体网格不能很好地描述齿尖形状，因此选用四面体网格划分方法，实际网格数31万；旋轮、上下模具以及芯模设置为解析刚体无需划分网格。(3)刻齿过程中局部塑性应变较大，需要在刻齿成形过程中对坯料设置网格重划分，重划分条件为干涉深度大于0.7，范围为区域网格重划分。(4)模拟过程中旋轮做进给运动的同时绕坯料的中心轴转动，在接触部位不仅存在滚动摩擦，也存在滑动摩擦；摩擦表现出高度的非线性特征，因此采用剪切摩擦进行简化处理；旋轮与坯料间的摩擦因子设置为0.05[11]。(5)实际旋压过程中加入石墨乳液作冷却液，旋压温度恒定在常温，因此忽略模拟成形过程中的温度变化，将仿真成形过程视为等温成形[12]，坯料与模具温度设为20 ℃。

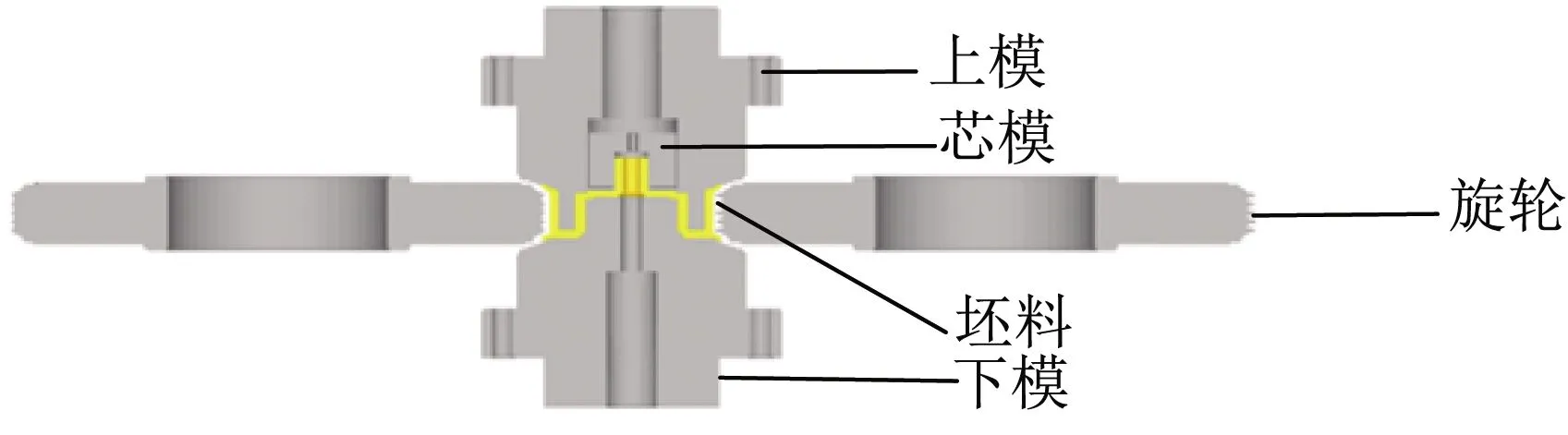
图4 模型中坯料及其他模具的位置Fig.4 Locations of workpice and other molds in the model

表1 V形带轮旋压成形参数Table 1 Spinning forming parameters of V- shaped belt wheel

2.2 模拟结果

2.2.1 刻齿成形过程

在刻齿成形过程中，坯料部分区域为减薄旋压。为防止成形过程中旋压力过大导致减薄区域坯料破裂，将刻齿成形分为第一道次粗齿成形和第二道次细齿成形。在第一道次成形初期，如图5所示，旋轮粗齿齿形部位先作用于坯料筒壁，接触部位开始向内凹陷。此时材料不仅在纵向上向两侧齿尖流动填充齿形，而且在横向上向未刻齿区域流动并有少量材料向已刻齿区域流动。在成形中期，粗齿齿形区域进一步与坯料贴合，此时金属沿径向发生剧烈变形，逐渐成形粗齿旋。压力随旋轮进给量的增加而增大，且开始时增大较快，至旋轮进给量达到一定值后又减缓[13]。在成形末期，粗齿旋轮与坯料完全啮合，粗齿齿形完全成形。

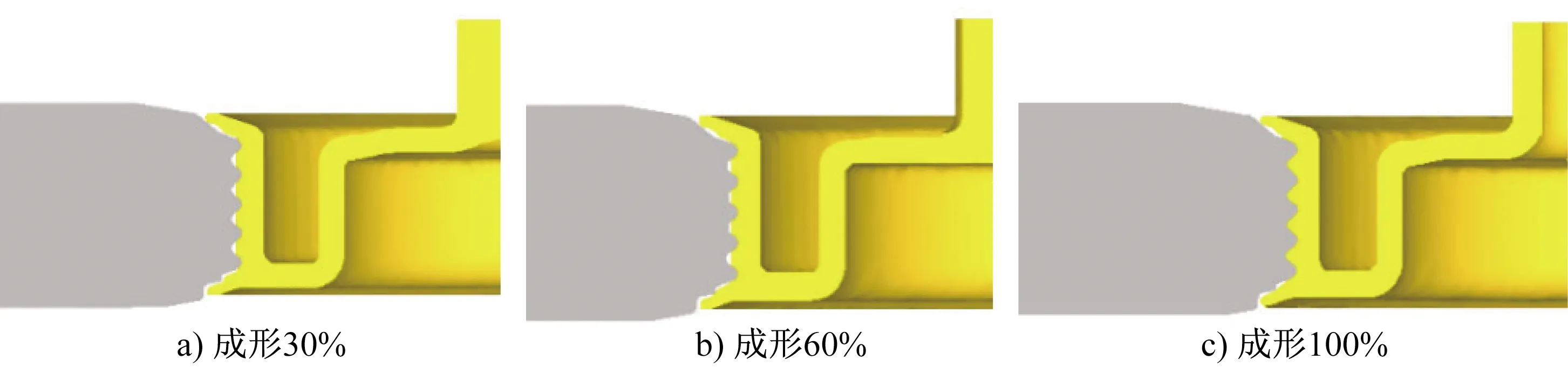
图5 第一道次成形图(左边为旋轮，右边为坯料)Fig.5 Forming diagram of the first working step (rotating wheel on the left and workpice on the right)

图6为第二道次细齿成形过程图。该道次在第一道次的基础上进一步细化齿形，以达到需要的齿形精度。

2.2.2 等效应力分布特征

刻齿成形过程伴随着区域减薄和增厚，旋压过程中坯料可能出现减薄破裂。因此在减薄区域，即在将成形的齿底区取5个点分析等效应力状态，如图7所示。图8为5个点的等效应力值随时间的变化。

图7 点追踪位置Fig.7 Point- tracking positions

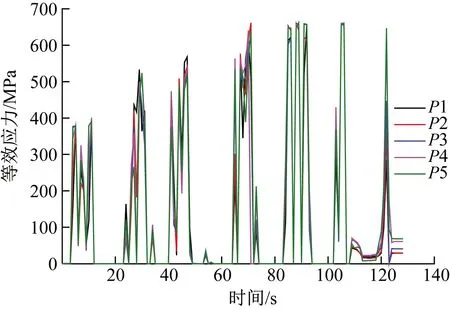
图8 追踪点处等效应力随时间变化曲线Fig.8 Variation curves of equivalent stress at tracking points with time

由图8可以看出，在成形过程中，5个追踪点的等效应力值均为正，点与点之间的等效应力变化趋势相同且等效应力值变化不大。这主要是因为5个点分布在同一条轴线上，同时与旋轮发生接触，进给深度相同，同一时间材料的变形抗力相同。由图9和图10可知，轮齿部位的等效应力沿周向分布较为均匀，越靠近旋轮与坯料接触区，等效应力越大，坯料与旋轮直接接触位置的等效应力最大，远离接触区域等效应力几乎为0。

图9 第一道次等效应力图Fig.9 Equivalent stress diagram of the first working step

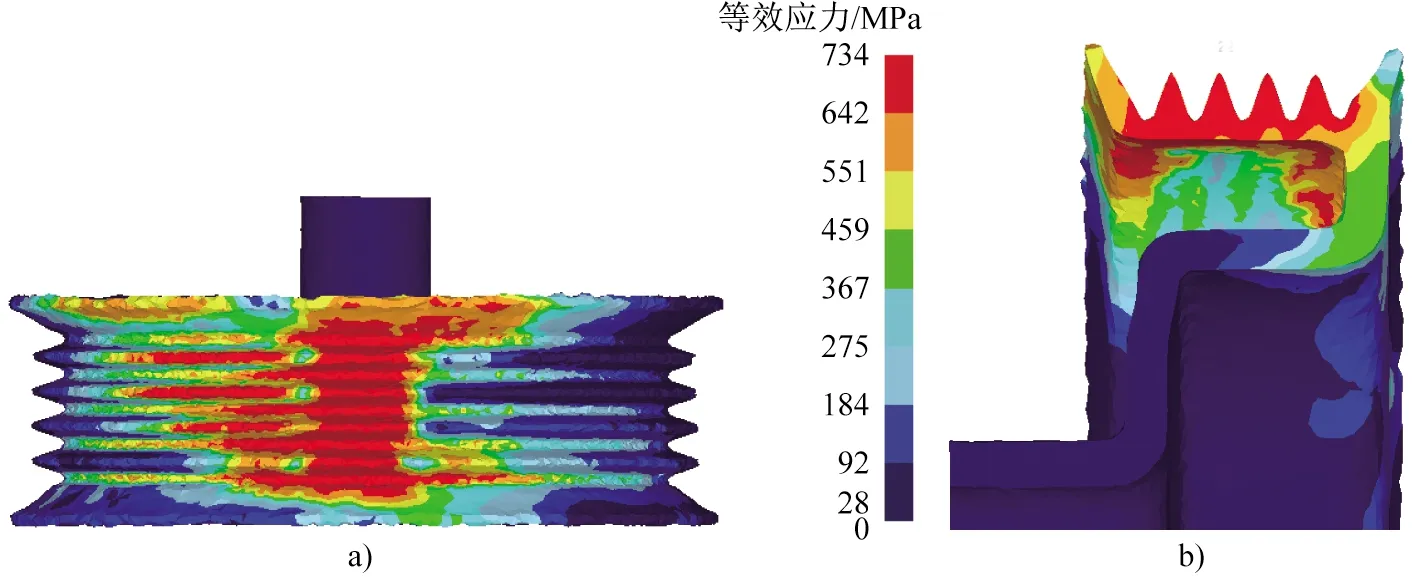
图10 第二道次等效应力图Fig.10 Equivalent stress diagram of the second working step

图9为第一道次成形时坯料所受等效应力状态。外筒壁刻齿成形区的应力主要为压应力，齿壁区承受的是拉应力。这是因为在粗齿旋轮进给过程中，外筒壁刻齿区大部分材料受到挤压逐渐填充齿形，而齿壁材料为了填充齿顶而受拉。由图9等效应力云图可知，粗齿成形区的等效应力最小为167 MPa，最大为668 MPa，说明在粗齿成形道次结束后坯料处于弹塑性应力状态，卸载后存在回弹。图10为第二道次成形时坯料所受等效应力状态。第二道次的最大等效应力值大于第一道次。一方面，这是由于经过第一道次成形后，材料变形抗力增大；另一方面，第二道次的进给量大于第一道次。第二道次刻齿成形区的等效应力为225～734 MPa，与第一道次相同，均处于弹塑性应力状态，卸载后，产生一定回弹。因此，为了防止实际生产过程中由于材料回弹而导致零件尺寸不达标的情况，刻齿完成后，在保持进给量不变的情况下继续保持刻齿状态一段时间，再取出坯料，以保证成形零件合格。

2.2.3 旋轮载荷

在旋压过程中，旋轮齿及旋轮中心轴所受载荷较大，易造成旋轮齿破裂和旋轮中心轴断裂。图11分别是第一、第二道次旋压过程中旋轮所受载荷随时间的变化。从图11可以看出，随着时间的增加，旋轮所受载荷先缓慢增加，但增量不大。这是由于坯料首先受到旋轮的挤压，此时旋轮与坯料刚接触，进给量不大，材料变形抗力小，故载荷增量不大。在时间为10和64 s左右时，第一道次和第二道次旋轮所受载荷均出现剧烈波动，并分别于22和76 s时达到最大值，为87和155 kN。这是因为坯料在旋轮的作用下产生塑性变形，发生加工硬化，变形抗力增加导致旋轮所受载荷增大。因此，在实际旋压过程中，旋轮承受的载荷至少要大于155 kN。

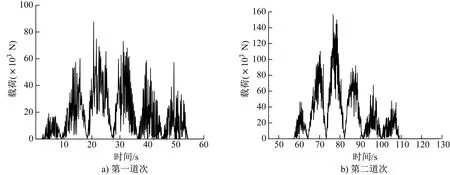
图11 旋轮所受载荷随时间的变化Fig.11 Dependence of load acting on the rotary wheel on time

3 成形试验结果与讨论

3.1 零件试制

使用60 t立式数控旋压机进行试模验证，零件工装和加工如图12所示。加工动作由PLC单元控制。石墨乳液用于润滑和冷却。加工零件如图13所示。从图13可以看出，模拟工艺参数实现了V形带轮旋压成形的全工序生产。

图12 60 t立式旋压机工装图Fig.12 Assembly diagram of the 60 t vertical spinning machine

图13 模拟成形零件与试制零件Fig.13 Simulated forming part and trial-producted part

3.2 试制零件与模拟成形件的验证

在同齿带传动过程中，为使带齿能顺利嵌入轮齿槽且不会打滑脱出齿槽，要求带齿与轮齿啮合时有一定的齿侧间隙。在带轮齿槽的齿形角及顶部、根部圆角半径已定的情况下，齿槽深度决定着轮齿与带齿间接触面积及径向间隙的大小。因此，齿间距和齿槽深度是确定最终成形零件是否达到标准的重要条件。在后处理中测量模拟成形件的尺寸数据，结果如图14所示。采用CV- 3100轮廓仪测量试制件的关键尺寸，结果如图15所示。可以看出，试制零件的齿间距分别为3.569、3.562、3.579、3.551 mm，与模拟件尺寸的误差分别为0.013、0.024、0.023、0.014 mm，最大误差小于0.7%。试制件的齿槽深度分别为3.447、3.370、3.369、3.381、3.376 mm，与模拟件尺寸误差分别为0.011、0.058、0.028、0.078、0.042 mm，最大误差小于2.3%。由此可知，仿真模拟得出的工艺参数实现了齿形带轮零件的全工序生产，模拟结果和实际成形零件在齿间距和齿槽深度等外形精度上具有良好的相符性，验证了本文建模方法的可行性。

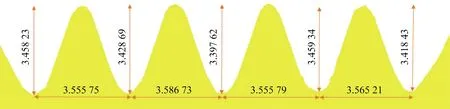
图14 模拟成形件尺寸Fig.14 Dimension of the simulated forming part

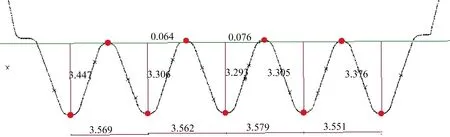
图15 试制零件轮廓线Fig.15 Outline drawing of the trial-produced part

4 结论

(1)基于Deform- 3D平台建立了V形带轮旋压成形有限元仿真模型，通过螺旋进给替代传统建模方法，将坯料的自转转化为旋轮绕静止坯料的阿基米德螺旋进给运动，并在上下模具与坯料之间设置黏着接触点使系统处于稳定状态，有效减少了计算量，实现了大旋比V形带轮旋压三维成形仿真，证明了建模的可行性。

(2)试制零件的齿间距与模拟件的最大误差小于0.7%。试制零件的齿槽深度与模拟件的最大误差小于2.3%，试制件与模拟件的相符度较高，证明了建模方法的可行性。

(3)实际旋压过程中，第一道次旋轮可承受载荷至少要大于87 kN，第二道次旋轮可承受载荷至少要大于155 kN。由于刻齿结束后零件存在回弹的可能，因此刻齿后在保持进给量不变的情况下应继续保持刻齿状态一段时间。