参数扰动下时滞忆阻神经网络的Lagrange稳定性
李梁晨 甘勤涛 蔺佳哲,3
(1陆军工程大学石家庄校区, 石家庄 050000)(2盲信号处理国家级重点实验室, 成都 610000)(3中国空气动力研究与发展中心计算空气动力研究所, 绵阳 621000)
第4种无源基本电路元件——忆阻器的概念最早由Chua[1]于1971年提出.2015年,Chua[2]再次对忆阻器的概念和分类进行了明确.在双极性周期性电信号下,理想忆阻器在V-I平面的电特性为一条捏滞回线,即忆阻器的阻值(称为忆阻)依赖于过去流经该器件的电荷总量.该特性可以由一些氧化物材料实现,并且具有一定的非易失性.2008年惠普实验室构造出Pt/TiO2/Pt结构的忆阻器,并且构建了器件的忆阻模型[3].该实验室于2010年使用忆阻实现了NAND等基本布尔逻辑[4],使得在同一器件中实现信息储存和处理变为可能.
Hu等[5]使用忆阻器在电路系统中模拟神经元突触连接构建了基于忆阻的神经网络电路.这种基于忆阻的神经网络在图像处理[6]、联想记忆[7-8]、机器学习[9]等领域有着广泛的应用前景.近年来,这类神经网络得到越来越多学者的关注.
Wu等[9]建立了时滞忆阻神经网络数学模型,并分析了模型平衡点的全局一致稳定性.此后一些关于忆阻神经网络稳定性[10-11]、同步性[12-13]、无源性[14-15]、耗散性[16-17]等动力学特性的研究成果相继问世.这些研究中都假设忆阻器的忆阻值在2个定值间切换,并且切换的条件只依赖于网络中神经元的实时状态.然而,这种假设忽视了忆阻器状态变化的过程,使得网络中的忆阻器失去了特有的记忆特性.Pershin等[18]也指出了该问题.
本文根据忆阻器的物理特性,构建一类荷控忆阻神经网络模型.网络中忆阻器的状态(忆阻值)由初始状态和在特定方向上通过器件的电荷量决定,网络的连接权值受通过相应忆阻器电荷量的影响连续变化.实际忆阻器在双极性周期性电信号下的V-I曲线与理想模型略有差异.这种差异很可能导致神经网络的稳定状态发生变化,而在以往的研究中该因素都被忽视.本文使用参数扰动来刻画这种差异,并通过分析网络的Lagrange稳定性研究其对忆阻神经网络动力学性态的影响.Lagrange稳定性研究的是整个系统的稳定性,若网络是Lagrange意义下稳定的,则可保证网络的平衡点、周期解、概周期解、混沌吸引子都在全局吸引集的范围内.Lyapunov意义下网络的全局稳定性也可视为全局吸引集为平衡点的Lagrange稳定的特殊情况[19-20].
本文通过构造Lyapunov函数,用线性矩阵不等式形式给出受参数变化范围影响的网络Lagrange稳定的充分条件,并根据网络自身参数给出全局指数吸引集估计.最后,通过数值实例说明理论结果.
1 网络建模
Strukov等[3]给出了惠普实验室制作的Pt/TiO2-x/Pt结构忆阻器的模型:
(1)
式中,v(t)为施加在忆阻器两端的电压;i(t)为通过忆阻器的电流;l为夹在2个金属电极间半导体薄膜的厚度;w(t)为电阻较低的掺杂区域的长度;ron、roff分别为忆阻器的最小和最大忆阻值;μ为忆阻器中离子迁移的平均速率.
由式(1)可推导出忆阻器忆阻值rmem(t)及其导数的表达式:


(2)
(3)
式中,w0为掺杂区域的初始长度.忆阻器的忆导值定义为mmem(t)=1/rmem(t),忆导值的导数满足
(4)
将这种忆阻器应用到神经网络电路中,代替模拟神经元突触的电阻,可得到图1中的忆阻神经网络电路.根据基尔霍夫电流定律,得到如下荷控忆阻神经网络模型:

(5)

令C([-τ,0],Rn)表示由连续函数ψ:[-τ,0]→Rn构成的Banach空间,其范数为‖ψ‖c=sups∈[-τ,0]|ψ(s)|.对任意常数S>0,定义其子集CS={ψ∈C:‖ψ‖c 定义1如果对于任意的S>0,存在常数κ=κ(S)>0使得‖x(t,ψ)‖<κ,ψ∈CS,t≥0,则称网络在Lagrange意义下是一致有界的. 定义2如果存在一个径向无界的正定函数V(x(t)),泛函κ∈C,正常数l、α,使得对网络的任意解x(t)=x(t,ψ),当V(x(t))>l,t≥0时,有V(x(t))-l≤κ(ψ)exp(-αt),则称网络是全局指数吸引的,紧集Ω:={x∈Rn,V(x) 图1 忆阻神经网络电路图 定义3若网络在Lagrange意义下一致有界并且是全局指数吸引的,则称网络在Lagrange意义下是全局指数稳定的. 本文对忆阻神经网络模型(5)做如下假设: 2)时滞τj(t)可导,且存在正常数τ、ωj,满足 3)外部输入Ii(t)有界,即存在正常数γi,使得|Ii(t)|≤γi(i=1,2,…,n). 在研究网络稳定性时将用到以下引理: 引理2[21]若M、E、T(t)为实矩阵,且T(t)满足TT(t)T(t)≤I(I为单位矩阵),则对任意ε>0有 MT(t)E+(MT(t)E)T≤ε-1MMT+εETE 首先,将模型(5)中的神经元状态方程改写成如下形式: (6) 其中 将式(6)改写成矩阵形式: (7) 其中 x(t)={x1(t),x2(t),…,xn(t)}T f(x(t))={f1(x1(t)),f2(x2(t)), …,fn(xn(t))}T g(x(t-τ(t)))={g1(x1(t-τ1(t))), P(t)={p1(t),p2(t),…,pn(t)}T 其中 G=[G1G2…Gn] Wi(t)=diag(Wi1,Wi2,…,Win) 式中,ei为第i个元素为1的n维列向量. 实验表明,忆阻器的实际阻值与理想模型存在一定差异[3],因此在研究忆阻神经网络的稳定性时,考虑一定的参数扰动.在模型(7)中引入参数扰动,得 (8) 式中,参数扰动ΔA、ΔB、ΔD满足 ΔA=H1T1(t)Z1 其中,H1、H2、H3、Z1、Z2、Z3为已知的常实数矩阵;T1(t)、T2(t)、T3(t)为未知的时变矩阵,满足 (9) 对于模型(8)的稳定性有如下结论. 定理1当A1~A3成立时,若存在正定矩阵K、M1、M2,正常数εi(i=1,2,…,9)和正定对角矩阵R、Q,使得下列线性矩阵不等式成立: (10) (11) 其中, Φ=-diag(ε1I,ε2I,ε3I,ε4I,ε5I,ε6I,ε7I, 则模型(8)是Lagrange意义下全局指数稳定的,且Π={x∈Rn|xTKx≤PTM2P}为模型(8)的一个全局指数吸引集,其中P={γ1/C1,γ2/C2,…,γN/CN}T. 证明构造径向无界的Lyapunov-Krasovskii泛函 式中,K为正定矩阵;Q=diag(q1,q2,…,qn)为正定对角矩阵.计算V(t)的导数 由假设1可得 (12) 由引理2,有 (13) 以及 2(xT(t)K+fT(x(t))Q)(-ΔDx(t)+ΔAf(x(t))+ (14) 由假设1和线性矩阵不等式(11),可得 x(t-τ(t))TKx(t-τ(t)) 由V(t)的定义可知 (15) V(t)≤xT(t)(K+QLf)x(t) (16) 综合式(12)~(16),可得 由线性矩阵不等式(10)及引理1可知,Ξ-ΓΦ-1ΓT<0.因此 其等价于 由引理3可知 式中,λ为方程λ=2-eλτ的根.因此,模型(8)是Lagrange意义下全局指数稳定的,且Π={x∈Rn|xTKx≤PTM2P}是它的一个全局指数吸引集. 在模型建立和定理1的证明中应注意以下方面: 1) 忆阻器具有极性,因此若将忆阻器反向接入网络,其阻值变化将恰好相反,模型(5)中相应忆阻器忆导的导数将取相反数. 3)定理1讨论了当激活函数满足Lipschitz连续条件时,网络Lagrange稳定的充分条件.忆阻器阻值在各阻态下小范围变化引起的参数扰动存在于判定不等式中,一方面影响判定条件,另一方面影响P、M2的取值,间接影响全局指数吸引集的范围估计. 4)若激活函数是有界的,不难推断出网络一定是Lagrange稳定的,但是其全局指数吸引集的范围仍有待估计.此时,参数扰动的影响将主要体现在对全局指数吸引集的范围估计. 5)本文中为处理忆阻神经网络模型参数变化所使用的重构模型方法,避免了文献[23]中使用定量分析方法造成的计算量过大的问题,所得条件保守性较弱,且计算量小.用这种方法处理模型,验证文献[23]例1中网络的稳定性仅需求解1个线性矩阵不等式,而根据该文中的定理3.1则需求解8个,且随着网络中神经元个数增加,差距将进一步拉大.此外,在文献[24]的证明过程中使用这种方法,亦可降低稳定性判据的计算量,且所得全局吸引集的估计范围更小,保守性更低. 本节以图2中的忆阻神经网络电路为例,通过数值模拟说明所建立的荷控忆阻神经网络模型与现有的2类忆阻神经网络模型的不同之处及优势,并验证定理1的可行性. 图2 由2个神经元构成的忆阻神经网络电路图 算例1假设图2中的忆阻器相同,且满足 忆阻器中离子迁移的平均速率为常数μ=10-14m2/(s·V).选取图2中的电阻和运算放大器为 外部输入Ii=0,传输时滞满足τi(t)=1+0.5tanh(t)s,i=1,2. 首先,用现有的2类切换型忆阻神经网络模型来描述本例中的忆阻神经网络,并分别用这2种模型进行仿真. 若采用文献[14]中的忆阻神经网络模型,则网络中忆阻器的忆阻值满足 网络神经元状态的描述方程则与模型(5)中一致.选取神经元状态初值x1(θ)=2 V,x2(θ)=2 V,θ∈[-1.5,0],对网络进行仿真,网络中忆阻器忆阻值的轨迹如图3所示. 对于文献[25]中的电压导数符号切换忆阻神经网络模型,其忆阻器的忆阻值满足 网络神经元状态的描述方程仍与模型(5)中一致.选取神经元状态初值x1(θ)=2 V,x2(θ)=2 V,θ∈[-1.5,0],对网络进行仿真,网络中忆阻器忆阻值的轨迹如图4所示. 对这2类模型的仿真显示,网络中忆阻器的忆阻值在某些时段出现高频率震荡.仿真中,每个点的间隔时间为0.01 s,而实际中忆阻器的忆阻值不会在这么短的时间内发生如此大的变化,即使施加在忆阻器两端的信号为高频双极周期信号,忆阻器的V-I特性曲线表现为一条直线,其作用如同普通的电阻.因此,用这2类模型来描述算例1中的忆阻神经网络,将与实际网络存在较大误差. 图5中忆阻值的轨迹符合忆阻器物理特性.因此,对于算例1中的忆阻神经网络,使用荷控忆阻神经网络模型(5)对其进行仿真,结果更符合实际. 选取如下3组初值: x1(θ)=2 V,x2(θ)=2 V,θ∈[-1.5,0] x1(θ)=-2 V,x2(θ)=-2 V,θ∈[-1.5,0] x1(θ)=2 V,x2(θ)=2 V,θ∈[-1.5,0] 分别在这3组条件下,使用荷控忆阻神经网络模型(5)对算例1中的忆阻神经网络进行仿真,网络中神经元状态的轨迹如图6所示. (a) 神经元x1 (b) 神经元x2 通过对比可看出,在初始条件φ1和φ2下,忆阻器的初始忆阻值相同,而网络的神经元状态初值不同,网络中神经元状态轨迹分别趋向于不同步的震荡.在初始条件φ1和φ3下,网络的神经元状态初值相同,而忆阻器的初始忆阻值不同,网络中神经元的状态轨迹趋向于不同的区域.而在现有模型中,忆阻器的忆阻值是由相应神经元的当前状态决定的,因此不会出现这种现象,同时忆阻器失去了其记忆特性.而在本文提出的荷控忆阻神经网络模型中,忆阻器的忆阻值由其初始忆阻值和从初始时刻到当前时刻流经忆阻器的电荷量决定.换言之,忆阻器的忆阻值受到相应神经元从初始时刻到当前时刻全部状态的影响,这体现了其记忆特性. 下面验证定理1中网络稳定性判据的可行性. 算例2设图2中的忆阻器满足 其他电路元件选择如下: 选取网络的外部输入为P(t)={cost,sint}T.假设网络中的参数扰动满足 通过计算可得 使用Matlab中的LMI工具箱计算定理1条件中的线性矩阵不等式(10)和(11),得到一组可行解.根据定理1,该忆阻神经网络是Lagrange稳定的,经计算得Ω={x∈R2|xTKx≤6.493 2}是网络的一个全局指数吸引集,其中 以模型(8)对图2中的电路进行仿真,选取20组不同的网络初值,满足 网络中存在和不存在参数扰动的情况下,在这20组初值下神经元状态轨迹如图7所示. (a) 神经元x1 (b) 神经元x2 由图7可看出,当网络中存在参数扰动时,网络的周期解发生了一定的偏移,但仿真结果与定理1的结论一致,忆阻神经网络的轨迹都收敛到所给出的全局吸引集内.这说明了本文给出的荷控忆阻神经网络模型(8)稳定性判据的可行性. 1) 本文所提出新模型的自反馈系数和连接权值随相应忆阻器阻值的变化而连续变化,保留了忆阻器记录在一定方向上流经器件的电荷量的特性,更符合实际,且更具有一般性. 2) 本文使用的重构模型方法亦可推广应用于传统忆阻神经网络模型的研究.本文推广了部分忆阻神经网络Lagrange稳定性和Lyapunov稳定性的研究成果. 3) 从数值仿真结果中可以看出,参数扰动使得网络的最终状态发生了变化.因此,若不考虑该因素,很可能导致网络在实际应用中的结果达不到预期效果.本文中考虑的参数扰动来自于忆阻器实际阻值与理想模型存在的差异,但还有其他一些因素也可能造成参数的扰动,比如环境温度的变化、磁场的变化,这些因素同样也可作用于非忆阻神经网络.因此,本文的结果对于忆阻神经网络及非忆阻神经网络的应用有实际意义.





2 网络稳定性
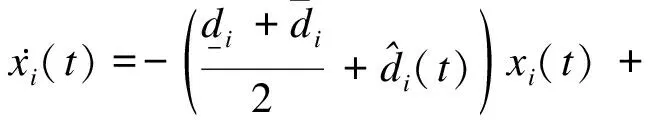

g2(x2(t-τ2(t))), …,gn(xn(t-τn(t)))}T


ΔB=H2T2(t)Z2
ΔD=H3T3(t)Z3
ε8I,ε9I,M1,M2)









3 数值算例













4 结论

