堆载及基坑开挖作用下被动桩水平受力及变形响应

杨 涛 童立元 潘皇宋

(东南大学岩土工程研究所， 南京 210096)

在城市交通网络形成过程中，既有地下桩基、管线和地铁隧道等地下构筑物相互影响越来越明显[1].随着基坑工程密度的加大，对已有地下构筑物产生叠加影响的因素逐渐增多.例如，基坑的开挖必然导致周边土体位移及应力场发生变化，从而对邻近桩基产生影响[2]；桩基附近的堆载会对桩基本身产生挤压效应，引起桩体的挠曲变形等[3].在目前的大多数研究中，对桩基水平受力变形的影响分析往往只考虑基坑开挖或堆载等单一因素，很少分析实际工程中常见的基坑开挖卸荷与堆载对桩基的综合作用，从而引发一些工程事故.因此，开展针对基坑开挖卸荷与堆载综合作用下邻近桩基受力变形的研究具有一定的工程实际意义.

国内外学者就基坑开挖或堆载对邻近桩基的影响开展了大量研究[4-5].Poulos等[6]运用有限元与边界元相结合的方法，分析了基坑开挖引起邻近桩基受力变形的影响因素.张爱军等[7]基于影像源法及Winkler地基模型，采用两阶段分析方法推导出基坑开挖引起的桩基响应数学解析解.郑刚等[8]以实测工程为案例，采用三维有限元法进行计算，分析了桩基和基坑间距、桩基刚度、桩顶竖向荷载和桩基顶部约束条件等对桩基附加弯矩、位移的影响.冯昌明等[9]基于布西奈斯克解及明德林位移解，提出了堆载作用下被动单桩竖向和水平向承载特性的分析方法.宋修广等[10]基于Flamant解得到条形荷载下的水平附加应力计算公式，并结合双参数地基模型，建立了被动桩的挠曲微分方程.竺明星等[11]对Ito局部塑性变形理论进行改进，以布西奈斯克改进解为基础，得到被动桩桩体被动荷载分布，并根据三参数非线性弹性地基梁模型，建立桩体微分方程组.

本文采用两阶段分析法，分析基坑开挖卸荷与堆载综合作用下邻近桩基的受力变形规律.首先，基于布西奈斯克水平应力解析解及明德林解析解，分别求出堆载作用及基坑开挖卸荷作用下桩基水平附加应力.其次，引入Kerr地基模型，建立被动桩的挠曲微分方程，利用有限差分数值计算方法，得到桩基挠曲微分方程的数学解析矩阵表达式.最后，通过实例分析验证所提方法的合理性和有效性，并以此为基础，针对堆载区域尺寸、堆载大小及基坑三维尺寸进行影响因素敏感性分析.

1 水平附加应力求解

1.1 堆载作用下的桩体处附加应力

在半无限空间弹性体表面作用有竖向集中力时，可利用布西奈斯克水平应力解析解求出弹性体内任意点的水平应力[12].在荷载作用范围内积分，便可求得不同堆载形式下土中应力分布.本文采用复合辛普森公式对布西奈斯克水平应力解析解的积分进行求解.如图1所示，将竖直向下的均布荷载分别在x、y方向上等分为n和m份，即每个子区间表示为 [xk,xk+1](k=0,1,…,n-1)及[yl,yl+1](l=0,1,…,m-1).若记

(1)

根据复合辛普森公式，上述均布荷载区域下的积分可表示为

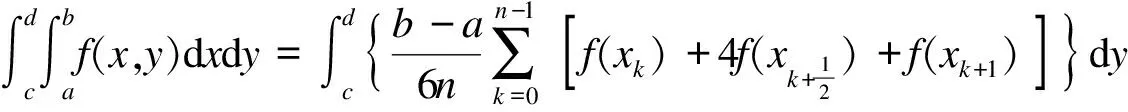
(2)

图1 堆载作用下被动桩受力示意图

将布西奈斯克水平应力解析解[12]代入双重积分式(2)中，便可得到矩形均布荷载下土体自由场中相应位置的水平应力.

1.2 基坑开挖引起的桩体处附加应力

计算前先进行如下假定：①土体为均质、弹性半空间体；②不考虑基坑开挖的时序效应，不考虑降水的影响；③开挖至坑底时，考虑坑底残余应力及围护墙遮拦效应，坑底释放的应力等效为坑底平面处竖直向上的均布荷载；④不考虑桩体存在及堆载对基坑开挖引起桩体处附加应力的影响；⑤仅考虑基坑单侧壁及坑底应力释放对桩体的影响.其中，均布荷载的具体计算参考文献[13]中的推导过程.

基于明德林解析解，得到基坑侧壁及坑底应力释放引起的桩基水平附加应力积分表达式，采用双重积分下的复合辛普森公式进行具体求解.

2 基于Kerr地基模型的分析方法

在弹性地基梁理论中，最常用的弹性地基模型为Winkler地基模型.该模型假设地基为一系列独立弹簧，但无法考虑土体剪切刚度.为此，部分学者引入第2个参数来反映弹簧间的剪切作用，其中应用较多的是Pasternak地基模型[14].Kerr地基模型通过引入第3个参数对双参数模型进行进一步优化，使得计算结果更为准确[15-16].

2.1 计算模型

堆载及基坑开挖卸载后，荷载经过土体的传递，变为作用于桩体的附加荷载.附加荷载下的Kerr地基模型见图2.图中，P为桩体所受附加荷

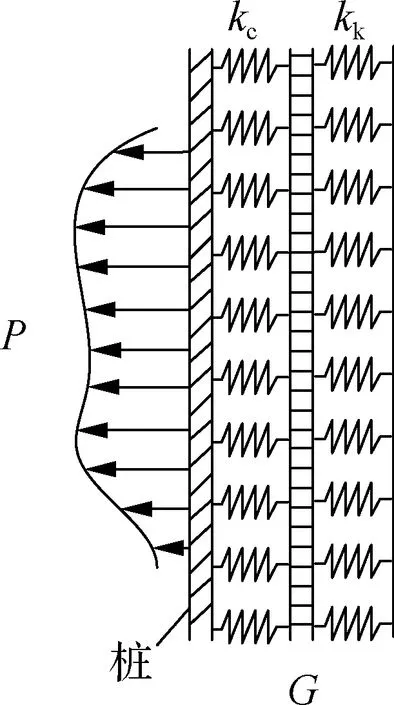
图2 Kerr地基模型示意图

载；G为地基土剪切刚度；kc、kk分别为第1、2层地基反力模量.

Kerr地基模型中，桩体假设为地基上的弹性长梁，在附加荷载作用下，桩体变形与弹簧层及剪切层变形一致.桩体挠曲微分方程为

(3)

式中，w2为剪切层的变形量；E为桩体弹性模量；I为桩体极惯性矩；dp为桩体直径.

2.2 地基参数选取

根据Tanahashi[17]提出的经验公式可知

(4)

式中，Es为地基土的弹性模量；μs为地基土的泊松比；δ为地基土的剪切层厚度，且参照文献[18]，δ≈11dp.

(5)

参照简化弹性空间法[20]，第1层地基反力模量为

kc=3kk

(6)

2.3 有限差分法求解

采用有限差分法对式(3)近似求解.将桩体s等分，桩顶至桩底节点编号为0，1，…，s.桩顶及桩底各增加3个虚拟节点，编号为-3，-2，-1，s+1，s+2，s+3(见图3).

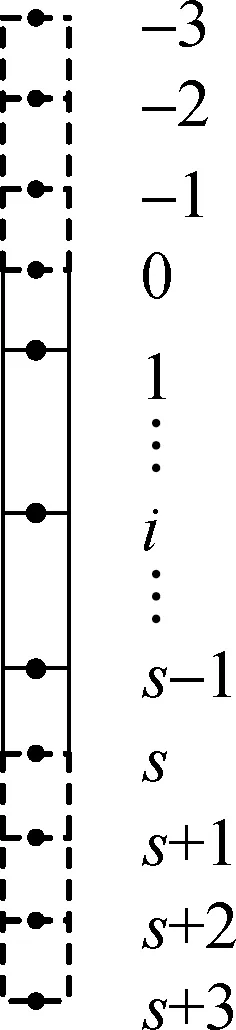
图3 桩体计算模型示意图

式(3)可简化为

u(6)+Au(4)+Bu(2)+Cu=D

(7)

式中，A为四阶导系数；B为二阶导系数；C为变量系数；D为常数项.

根据高阶导数的有限差分近似替代原则，式(7)可等效为s+1个方程.因增设了6个虚拟节点，s+1个方程中共包含s+7个未知数.假设桩顶自由无外力，桩底固定，可得边界条件的有限差分近似表达式.结合上述s+1个方程，消去多余未知量，最终可得桩体挠曲微分方程矩阵表达式为

Ku=F

(8)

式中，F={D0,D1,D2,…,Di,…,Dn-2,Dn-1,Dn}T为外荷载列向量；u={u0,u1,u2,…,ui,…,us-2,us-1,us}T为桩体节点水平位移列向量；K为桩体水平刚度矩阵，且

3 计算实例分析

利用基于Kerr地基模型的两阶段分析法，求解基坑开挖和堆载综合作用下桩体的受力变形规律，并与其他方法结果进行对比，验证该方法的正确性.

3.1 数值模拟验证

图4为计算模型尺寸及俯视图.由图可知，基坑长宽分别为30和20 m，开挖深度为10 m.堆载区域长宽分别为10和5 m，荷载为150 kPa.桩体直径为1 m，桩深20 m，距离基坑边界及堆载边界均为10 m.采用有限差分数值软件进行模拟，土体本构采用摩尔库伦模型，基坑围护结构及桩体采用弹性模型.各结构参数见表1.

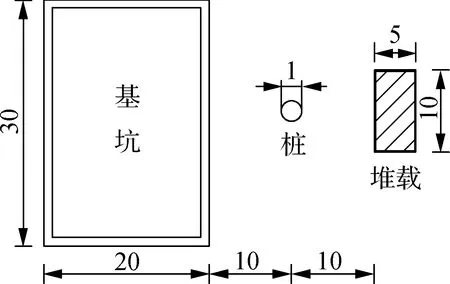
图4 模型尺寸及俯视图(单位：m)

表1 结构参数

图5为不同外加荷载引起的桩体附加应力.图中，Pd为堆载引起的附加应力；Pb为坑底卸荷引起的附加应力；Pc为侧壁卸荷引起的附加应力；Pz为堆载和基坑开挖卸荷综合作用引起的附加应力.由图可知，基坑侧壁卸荷对桩体水平受荷影响最大，堆载次之，基坑坑底卸荷最小.三者引起的水平附加应力分布最大值出现的位置不同：基坑侧壁卸荷引起的水平附加应力最大值出现位置主要由基坑开挖深度决定，位于开挖面之上2～3 m；堆载引起的水平附加应力最大值出现在地表下5 m左右的位置；坑底卸荷引起的附加应力最大值出现在桩底位置.综合作用下，桩体处最大水平附加应力为21.80 kPa，出现在地表下6 m处.此外，坑底卸荷引起的桩体水平附加应力最大值为基坑侧壁卸荷作用下桩体水平附加应力最大值的1/3左右，故在计算中不可忽略.

图5 桩体水平附加应力

利用本文方法和数值模拟得到的桩体挠度见图6.由图可知，本文方法与数值模拟结果较为吻合，表明本文方法具有一定的可靠性.2种计算方法所得结果在桩顶附近略有差别，原因是数值模拟中模型尺寸的边界效应会对分析单元的计算产生影响.

图6 桩体挠度

3.2 案例验证

文献[9]基于双参数地基模型，得到了边长为6 m、均布荷载为20 kPa的正方形堆载区引起的桩体挠曲变形，桩体与堆载区边界净距为2 m，桩长为21 m，直径为0.5 m，桩土弹性模量之比为8 000，土体泊松比为0.3.选取此案例，采用本文方法进行对比验证，结果见图7.由图可知，本文方法与文献[9]方法所得结果在桩体最大挠度数值及其出现位置等方面具有较好的一致性，由此证明了本文方法的可行性.

图7 堆载作用下桩体挠度对比图

4 桩体水平变形影响因素分析

根据不同的堆载区域尺寸、堆载大小及基坑三维尺寸，构造了25个工况，以此分析不同因素对桩体水平位移的影响.其中，基本工况设定为：堆载区域长、宽分别为10和5 m，荷载为150 kPa，基坑三维尺寸为30 m×20 m×10 m.

4.1 堆载区尺寸、堆载大小的影响

图8为不同堆载工况下计算所得的桩体挠曲变形曲线.图中，Lc为堆载区域长边长度；Ld为堆载区域短边长度；Pt为堆载大小.由图8(a)可知，当堆载区域长边由5 m增加到15 m时，桩体最大挠度值由1.18 mm增加到1.42 mm，增幅为20.3%.当堆载区域短边由1 m增加到10 m时，桩体最大挠度值由1.10 mm增加到1.51 mm，增幅为37.3%.由图8(b)可知，当堆载由50 kPa增加到250 kPa时，桩体最大挠度值由1.02 mm增加到1.56 mm，增幅为52.9%.由此可知，各因素对桩体水平位移的敏感性由大到小排列顺序为：堆载大小、堆载区域短边长度、堆载区域长边长度.因此，在工程实际中要规避集中堆载，尽量将堆载区划分为长条状.

4.2 基坑三维尺寸的影响

图9为不同基坑三维尺寸下计算所得的桩体挠曲变形曲线.图中，Lk为基坑开挖面长边边长；Lj为基坑开挖面短边边长；Hd为基坑开挖深度.由图9(a)可知，随着基坑开挖面长边长度从20 m增至40 m，桩体最大挠度值增加了0.21 mm，增幅为18.1%；随着基坑开挖面短边长度从10 m增至30 m，桩体最大挠度值增加了0.03 mm，增幅为2.4%.由图9(b)可知，随着开挖深度从5 m增至25 m，桩体最大挠度值增加了2.7 mm，增幅为397.1%，并且随着开挖深度的变化，桩体挠度分布形式出现明显不同.经过上述对比研究，在不同基坑三维尺寸条件下，各因素对桩体水平位移的敏感性由大到小排列顺序为：开挖深度、开挖面长度、开挖面宽度.因此，建议在工程实际中对每层土体采用梯次开挖，先开挖远离桩体的土体.

(c) 堆载大小

(a) 开挖面长边长度

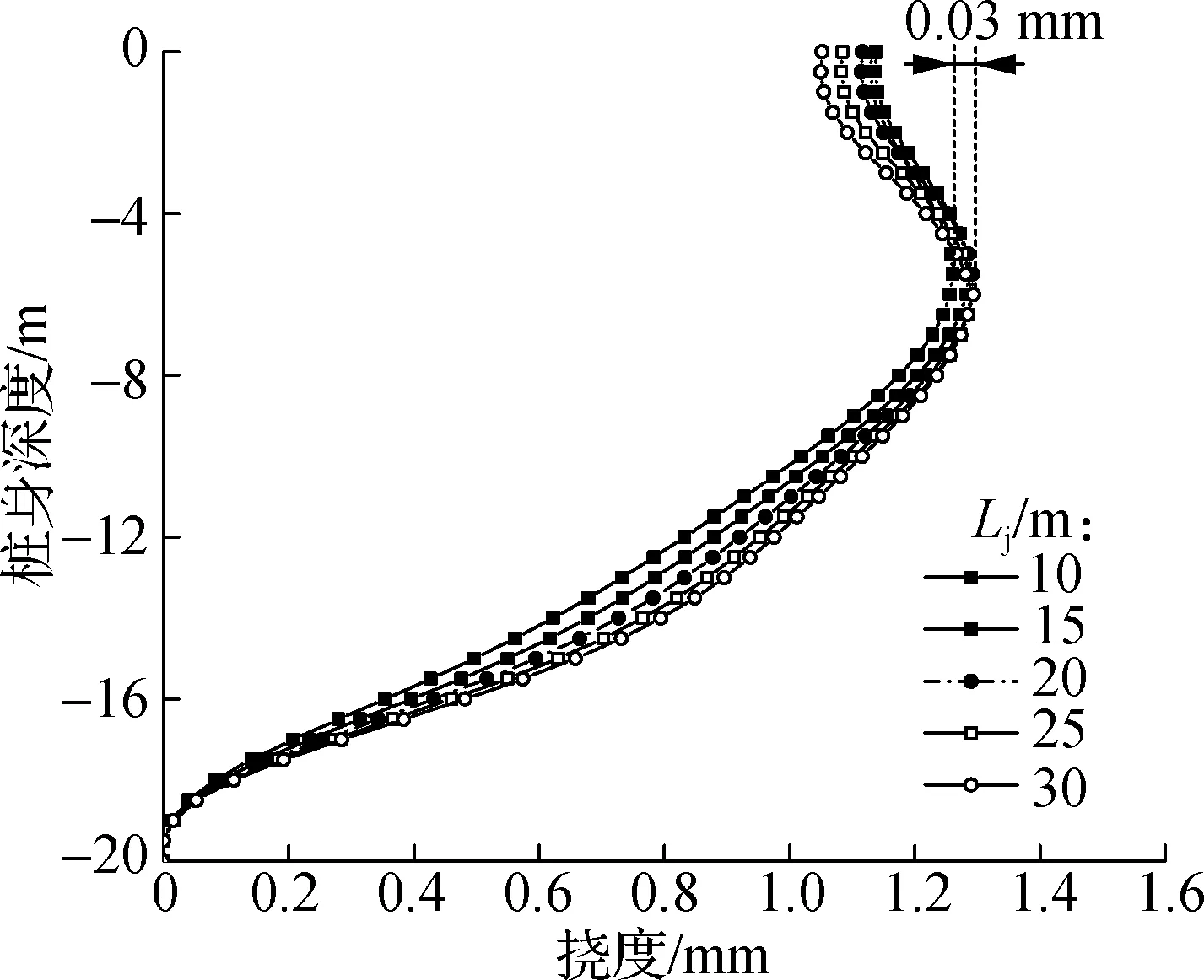
(b) 开挖面短边长度

(c) 开挖深度

5 结论

1) 本文基于Kerr地基模型建立了桩体挠曲变形计算方法.采用有限差分法推导出堆载及基坑开挖作用下桩体挠曲微分方程的数学矩阵表达式，并通过实例分析证明了其可行性和正确性.

2) 坑底卸荷引起的桩体最大水平附加应力是基坑侧壁卸荷引起的桩体最大水平附加应力的1/3左右.因此，在分析计算基坑开挖卸荷引起的桩体水平受力及变形时，不能仅考虑侧壁卸荷对桩体的影响.

3) 在堆载区尺寸、堆载大小中，对桩体水平位移的敏感性由大到小排列顺序为：堆载大小、堆载区域短边边长、堆载区域长边边长.建议工程实际中要规避集中堆载，尽量使堆载物呈长条状分布.

4) 在基坑三维尺寸中，对桩体水平位移的敏感性由大到小排列顺序为：开挖深度、开挖面长度、开挖面宽度.其中，基坑开挖深度对桩体水平位移的影响远大于开挖面尺寸的影响，建议实际开挖过程中尽量采用梯次开挖方式.