两个正交投影算子组合的性质

蒋万林，左可正，李 昱

(湖北师范大学数学与统计学院，湖北 黄石 435002)

1 预备引理

对于矩阵A∈n×n，若A2=A，称A为幂等矩阵;若A3=A，称A为三幂等矩阵;若A2=In，称A为对合矩阵;若存在k∈N+，使得Ak=0，称A为幂零矩阵;若AA†=A†A，称A为EP阵．

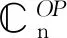
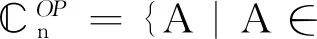
定义1[1-2]设矩阵A∈m×n，若矩阵X∈n×m满足下列条件：

1)AXA=A，2)XAX=X，3)XAk+1=Ak，

则称X为矩阵A的Moore-Penrose逆，记为A†．

A†总是存在且唯一的．

定义2[1-2]设矩阵A∈n×n，Ind(A)=k，若矩阵X∈n×n满足下列条件:

1)AXA=A，2)XAX=X，3)XAk+1=Ak，

则称X为矩阵A的Drazin逆，记为AD.当k=1时，AD称为是A的群逆，记为AD=A#．

若A#存在，则唯一.A#存在当且仅当Ind(A)≤1.

对于矩阵A∈n×n，分别用A，A，AD，†，A◊，A表示矩阵A的核心逆[3]，核-EP逆[4]，DMP-逆[5]，BT-逆[6]，弱群逆[7]．

在文[13]中，Benítez研究了两个正交投影算子P和Q的线性组合aP+bQ(ab≠0)的谱和秩，分别给出了两个正交投影算子的组合aP+bQ是EP阵，可对角化的，幂零矩阵，幂等矩阵，三幂等矩阵，对合矩阵，广义投影算子，超广义投影算子的一些性质，给出了在特殊条件下aP+bQ的Moore-Penrose逆的表示.在P和Q相乘不可交换的条件下，给出了aP+bQ是三幂等矩阵，对合矩阵，超广义投影算子的充要条件，并证明了aP+bQ不可能是幂零矩阵，幂等矩阵以及广义投影算子．

关于两个幂等矩阵P和Q的组合的研究有很多，例如，Koliha[14]证明了当a，b∈且ab≠0，a+b≠0时，r(aP+bQ)=r(P+Q).Tian[15]给出了关于r(P-Q)，r(P+Q)，r(PQ-QP)的一些秩等式.Deng[16]给出了在一些特殊条件下P+Q，P-Q的Drazin逆表达式．

进一步地，左可正[17]给出了两个幂等矩阵P和Q的组合aP+bQ+cPQ(ab≠0)的秩的重要等式，即证明了当a+b+c=0时，

r(aP+bQ+cPQ)=r(P-Q);

当a+b+c≠0时，

r(aP+bQ+cPQ)=r(P+Q).

在文[18]中，左可正研究了两个正交投影算子P和Q的组合aP+bQ-cPQ-dQP的可逆性条件，给出了在特殊条件下，aP+bQ-cPQ-dQP的Moore-Penrose逆的显示表达式.在文[19]中，左可正又证明了只有当两个正交投影算子P和Q相乘可交换时，aP+bQ+cPQ才有可能是正交幂等阵．

本文主要利用矩阵的CS-分解，研究两个正交投影算子P和Q的组合aP+bQ+cPQ分别在条件PQ=QP以及PQ≠QP下，是EP阵，可对角化矩阵，幂零矩阵，幂等矩阵，三幂等矩阵，对合矩阵的完全刻画．

CS-分解是研究两个正交投影算子的重要工具，利用CS-分解可以得到两个正交投影算子的组合的谱和秩的性质[13].CS-分解与两个子空间的主角密切相关[20],这些主角是扰动理论中的重要概念[21]．

其中C，S都是对角元为正实数的p阶对角方阵，且C2+S2=Ip.在P和Q的表达式中，对应位置的单位矩阵I和零矩阵有相同的阶数．

在CS-分解中，令

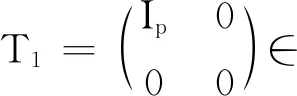
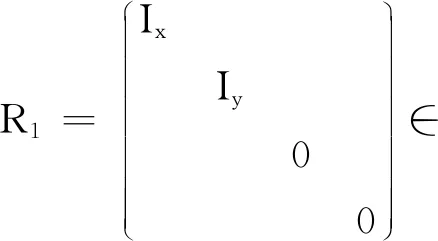
(1)

则

P=U(T1⊕R1)UH，Q=U(T2⊕R2)UH.

(2)

通过恰当的置换，对T1和T2中的元素进行重排，可设

(3)

令

i=1，2，…，p.

(4)

显然有

(5)

从而，

aP+bQ+cPQ=U((aT1+bT2+cT1T2)⊕

(aR1+bR2+cR1R2))UH=

(6)

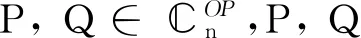
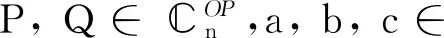
(aP+bQ+cPQ)†=

(aP+bQ+cPQ)](In-Π)+
{[(a+b+c)†-a-1-b-1]PQ+

a-1P+b-1Q}Π ，

其中，

2 主要结果

1)σ(aP+bQ+cPQ)⊂{0，a，b，a+b+c};

2)当a+b+c=0时，r(aP+bQ+cPQ)=r(P)+r(Q)-2r(PQ)=r(P-Q);当a+b+c≠0时，r(aP+bQ+cPQ)=r(P)+r(Q)-r(PQ)=r(P+Q);

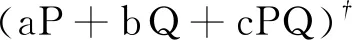
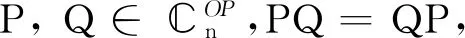
P=U(Ix⊕Iy-x⊕0⊕0)UH，

Q=U(Ix⊕0⊕Iz-x⊕0)UH，

(7)

则

aP+bQ+cPQ

=U((a+b+c)Ix⊕aIy-x⊕bIz-x⊕0)UH，

(8)

从而，

σ(aP+bQ+cPQ)⊂{0，a，b，a+b+c}.

2)结合文[17]中的结论，可知

当a+b+c=0时，

r(aP+bQ+cPQ)=

(y-x)+(z-x)=y+z-2x=

r(P)+r(Q)-2r(PQ)=r(P-Q);

当a+b+c≠0时，

r(aP+bQ+cPQ)=

x+(y-x)+(z-x)=y+z-x=

r(P)+r(Q)-r(PQ)=r(P+Q).

3)由文[18]中定理1的结果即得．

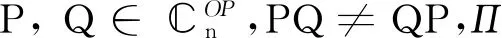
1)若θ∈Θ(P，Q)，η∈，η2=(a+b+ccos2θ)2-4absin2θ，则

若λ∈σ(aP+bQ+cPQ){0，a，b，a+b+c}，则存在θ∈Θ(P，Q)使得

其中，η2=(a+b+ccos2θ)2-4absin2θ．

2)r(PQ-QP)≤r(aP+bQ+cPQ).特别地，若PQ-QP可逆，则aP+bQ+cPQ可逆．

3)r((aP+bQ+cPQ)(I-Π))=r(PQ-QP)．

证明1)由(6)式有

σ(aP+bQ+cPQ)=

(9)

由(4)式知，Xi的特征多项式为

fXi(λ)=λ2-(a+b+ccos2θi)λ+absin2θi，

所以Xi的谱

σ(Xi)=

其中，

η2=(a+b+ccos2θi)2-4absin2θi.

(10)

因为σ(Xi)⊂σ(aP+bQ+cPQ)，i=1，2，…，p，所以

从而1)的前部分得证．

反过来由(9)式知，

σ(aP+bQ+cPQ){0，a，b，a+b+c}=

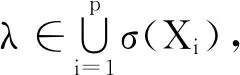
这样1)的后部分得证．

2)因为|Xi|=absin2θi≠0，由(5)式知，(aT1+bT2+cT1T2)∈2p×2p可逆．

由(6)式知，r(aP+bQ+cPQ)≥r(aT1+bT2+cT1T2)=2p，因为r(PQ-QP)=2p，所以r(PQ-QP)≤r(aP+bQ+cPQ).若PQ-QP可逆，则r(PQ-QP)=n，从而r(aP+bQ+cPQ)=n，即aP+bQ+cPQ可逆．

3)因为(aP+bQ+cPQ)(I-Π)=U((aT1+bT2+cT1T2)⊕0)UH，所以

r((aP+bQ+cPQ)(I-Π))=

2p=r(PQ-QP)．

λ∈σ(aP+bQ+cPQ)⟺

证明必要性.根据(3)式，由于

(11)

所以σ(T1T2)={cos2θi|θi∈Θ(P，Q)}∪{0}.取任意λ∈σ(aP+bQ+cPQ){0，a，b，a+b+c}，由定理2知，存在θ∈Θ(P，Q)以及η∈，η2=(a+b+ccos2θ)2-4absin2θ，使得

(12)

因此存在μ∈σ(T1T2)，使得μ=cos2θ.再结合(10)式和(12)式得出

λ2-(a+b)λ+ab=μ(ab+cλ)，

由于λ∈σ(aP+bQ+cPQ){0，a，b，a+b+c}，所以ab+cλ≠0，从而

(13)

因为σ(T1T2)⊂σ(PQ)，所以μ∈σ(PQ)．

充分性.假设μ∈σ(PQ)由(13)式给出，其中λ∈{0，a，b，a+b+c}，则有μ≠0且μ≠1，否则λ∈{a，b}或λ∈{0，a+b+c}，与假设矛盾．

对任意θ∈Θ(P，Q)，因为

σ(PQ)=σ(T1T2)∪σ(R1R2)，

其中，σ(T1T2)={cos2θi|θi∈Θ(P，Q)}∪{0}，σ(R1R2)={0，1}，从而μ∈σ(T1T2)．

由(11)式知，存在θ∈{θ1，θ2，…，θp}，使得μ=cos2θ.由(13)式，知

由上式，可得

λ2-(a+b+ccos2θ)λ+4absin2θ=0.

记η2=(a+b+ccos2θ)2-4absin2θ，从而

注记1定理3是文[13]中定理2.8的推广．

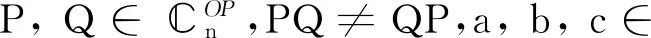
证明由(6)式，知aP+bQ+cPQ可对角化⟺aT1+bT2+cT1T2与aR1+bR2+cR1R2可对角化.而aR1+bR2+cR1R2是对角的，再结合(5)式知，aP+bQ+cPQ可对角化等价于每个Xi，i=1，2，…，p都可对角化.由(3)式知，Xi的特征多项式为

fXi(λ)=λ2-(a+b+ccos2θi)λ+absin2θi，

显然fXi(λ)有两个不同的根当且仅当(a+b+ccos2θi)2≠4absin2θi，因此若(a+b+ccos2θi)2≠4absin2θi，此时Xi可对角化.若(a+b+ccos2θi)2=4absin2θi，fXi(λ)有两个相同的特征值，此时若Xi可对角化，则存在一个可逆矩阵K∈2×2，使得Xi=K-1diag(λ，λ)K=λI2，这与(4)式矛盾.从而Xi可对角化当且仅当(a+b+ccos2θ)2≠4absin2θ．

注记2定理4是文[13]中推论2.9的推广．

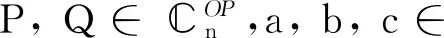
证明当PQ=QP时，结论显然成立．

当PQ≠QP时，由(6)式知，aR1+bR2+cR1R2是对角阵，而对角阵是EP阵.又因为aT1+bT2+cT1T2可逆，所以aT1+bT2+cT1T2也是EP阵，从而aP+bQ+cPQ是EP阵．

注记3由于X=aP+bQ+cPQ是EP阵，此时有

下面分别讨论在条件PQ=QP，PQ≠QP下aP+bQ+cPQ是幂零矩阵，幂等矩阵，三幂等矩阵，对合矩阵的充要条件.由于本文研究P，Q的组合的性质，因此只讨论P，Q≠0的情况．

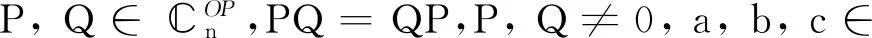
1)aP+bQ+cPQ是幂零矩阵的充分必要条件是a+b+c=0，P=Q=PQ．

2)aP+bQ+cPQ是幂等矩阵的充分必要条件是下列任一命题成立：

i)a+b+c∈{0，1}，a=1，b=1;

ii)a+b+c∈{0，1}，a=1，PQ=Q;

iii)a+b+c∈{0，1}，b=1，PQ=P;

iv)a+b+c∈{0，1}，P=Q;

v)a=1，b=1，PQ=0．

3)aP+bQ+cPQ是三幂等矩阵的充分必要条件是下列任一命题成立：

i)a+b+c∈{0，-1，1}，a∈{-1，1}，b∈{-1，1};

ii)a+b+c∈{0，-1，1}，a∈{-1，1}，PQ=Q;

iii)a+b+c∈{0，-1，1}，b∈{-1，1}，PQ=P;

iv)a+b+c∈{0，-1，1}，P=Q;

v)a∈{-1，1}，b∈{-1，1}，PQ=0．

4)aP+bQ+cPQ是对合矩阵的充分必要条件是下列任一命题成立：

i)a+b+c∈{-1，1}，a∈{-1，1}，b∈{-1，1}，r(P+Q)=n;

ii)a+b+c∈{-1，1}，a∈{-1，1}，P=In;

iii)a+b+c∈{-1，1}，b∈{-1，1}，Q=In;

iv)a+b+c∈{-1，1}，P=Q=In;

v)a∈{-1，1}，b∈{-1，1}，PQ=0，P+Q=In．

证明1)必要性.由(7)式知，aP+bQ+cPQ可对角化，若aP+bQ+cPQ是幂零矩阵，则

aP+bQ+cPQ=0.

(14)

将(14)式乘P，可得

aP+(b+c)PQ=0，

(15)

再将(15)式乘Q，可得

aPQ+(b+c)PQ=0，

(16)

又因为a≠0，结合(15)式和(16)式，可得P=PQ．

类似可证明Q=PQ，从而P=Q=PQ.此时(14)式变为(a+b+c)P=0，因为P≠0，所以a+b+c=0．

充分性.当a+b+c=0，P=Q=PQ时，aP+bQ+cPQ=0，因此aP+bQ+cPQ是幂零矩阵．

2)必要性.易知

(a+b+c)2=a+b+c⟺a+b+c∈{0，1}.

利用(7)式和(8)式的记号，若aP+bQ+cPQ是幂等矩阵，进行如下分类讨论.

a)当x>0，y-x>0，z-x>0时，有a+b+c∈{0，1}，a=1，b=1．

b)当x>0，y-x>0，z-x=0时，有a+b+c∈{0，1}，a=1，此时，

P=U(Ix⊕Iy-x⊕0)UH，

Q=U(Ix⊕0⊕0)UH，PQ=Q.

c)当x>0，y-x=0，z-x>0时，有a+b+c∈{0，1}，b=1，此时，

P=U(Ix⊕0⊕0)UH，

Q=U(Ix⊕Iz-x⊕0)UH，PQ=P.

d)当x>0，y-x=0，z-x=0时，有a+b+c∈{0，1}，此时，

P=U(Ix⊕0)UH，Q=U(Ix⊕0)UH，P=Q.

e)因为P，Q≠0，当x=0时，y-x，z-x都是大于0的，此时，

P=U(Iy-x⊕0⊕0)UH，

Q=U(0⊕Iz-x⊕0)UH，PQ=0.

由a)—e)，必要性得证．

充分性.利用(7)式和(8)式，直接验证即得．

3)易知(a+b+c)3=a+b+c⟺a+b+c∈{0，-1，1}，证明类似于上述2)的证明．

4)必要性.若aP+bQ+cPQ是对合矩阵，则(8)式中的第四分块不能出现，否则与aP+bQ+cPQ是对合矩阵相矛盾．

易知(a+b+c)2=1⟺a+b+c∈{-1，1}，利用(7)式和(8)式的记号，进行如下分类讨论.

a)当x>0，y-x>0，z-x>0时，有a+b+c∈{-1，1}，a∈{-1，1}，b∈{-1，1}，此时，

P=U(Ix⊕Iy-x⊕0)UH，

Q=U(Ix⊕0⊕Iz-x)UH，r(P+Q)=n.

b)当x>0，y-x>0，z-x=0时，有a+b+c∈{-1，1}，a∈{-1，1}，此时，

P=U(Ix⊕Iy-x)UH，Q=U(Ix⊕0)UH，P=In.

c)当x>0，y-x=0，z-x>0时，有a+b+c∈{-1，1}，b∈{-1，1}，此时，

P=U(Ix⊕0)UH，Q=U(Ix⊕Iz-x)UH，Q=In.

d)当x>0，y-x=0，z-x=0时，有a+b+c∈{0，1}，此时，

P=U(Ix)UH，Q=U(Ix)UH，P=Q=In.

e)因为P，Q≠0，当x=0时，y-x，z-x都是大于0的，有a∈{-1，1}，b∈{-1，1}，此时，

P=U(Iy-x⊕0)UH，

Q=U(0⊕Iz-x)UH，PQ=0，P+Q=In.

由(a)—(e)，必要性得证．

充分性.利用(7)式和(8)式，直接验证即得．

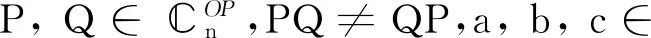
1)aP+bQ+cPQ不是幂零矩阵．

2)aP+bQ+cPQ不是幂等矩阵．

证明1)反证法.因为PQ≠QP，若aP+bQ+cPQ是幂零矩阵，则aT1+bT2+cT1T2是幂零矩阵且aT1+bT2+cT1T2这块一定存在，而这与aT1+bT2+cT1T2是可逆矩阵相矛盾，因此aP+bQ+cPQ不是幂零矩阵．

2)反证法.若aP+bQ+cPQ是幂等矩阵，由定理2知，aT1+bT2+cT1T2可逆，结合(6)式知

aT1+bT2+cT1T2=I2p.

(17)

因为(4)式中bcosθisinθi≠0，这与(1)式相矛盾，因此aP+bQ+cPQ不是幂等矩阵．

注记4定理7为文[13]中定理2.11(i)，(iv)的推广，当c=0时，即为定理2.11(i)，(iv)．

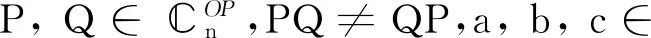
1)aP+bQ+cPQ是三幂等矩阵的充分必要条件是Θ(P，Q)={θ}，(aP+bQ+cPQ)2(In-Π)=In-Π，且下列任一命题成立：

iv)a+b+ccos2θ=0，absin2θ=-1，PΠ=QΠ=0．

2)aP+bQ+cPQ是对合矩阵的充分必要条件是Θ(P，Q)={θ}，(aP+bQ+cPQ)2(In-Π)=In-Π，且下列任一命题成立：

iii)a+b+ccos2θ=0，absin2θ=-1，Π=0．

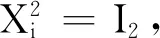
(aP+bQ+cPQ)2(In-Π)=In-Π.

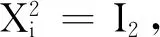
a+b+ccos2θi=0，absin2θi=-1.

(18)

由(1)式知，此时R1=Ix⊕Iy⊕0⊕0，R2=Ix⊕0⊕Iz⊕0，则

aR1+bR2+cR1R2=

(a+b+c)Ix⊕aIy⊕bIz⊕0.

(19)

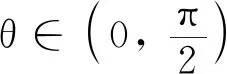
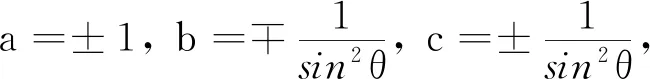
R1=Ix⊕Iy⊕0，R2=Ix⊕0⊕0.

R1=Ix⊕0⊕0，R2=Ix⊕Iz⊕0.

c)当x>0，y=0，z=0时，有(a+b+c)3=(a+b+c)，即a+b+c∈{0，-1，1}.根据a+b+c的不同取值，再对c)进行如下分类讨论.

c1)若a+b+c=0，则-csin2θ=0，又因为sin2θ≠0，所以c=0，此时,

c=0，R1=R2=Ix⊕0.

b2sin2θ-bcos2θ-1=0.

(20)

或

R1=R2=Ix⊕0.

(21)

c3)若a+b+c=1，类似于c2)的证明，可得

R1=R2=Ix⊕0，

(22)

或

R1=R2=Ix⊕0.

(23)

R1=Iy⊕0，R2=0⊕0.

R1=0⊕0，R2=Iz⊕0.

f)当x=0，y=0，z=0时，R1=R2=0，此时,

a+b+ccos2θ=0，absin2θ=-1，

PΠ=QΠ=0.

因此，由a)，d)，(20)式及(22)式可得命题i);由b)，e)，(21)式及(23)式可得命题ii);由c1)可得命题iii);由f)可得命题iv)．

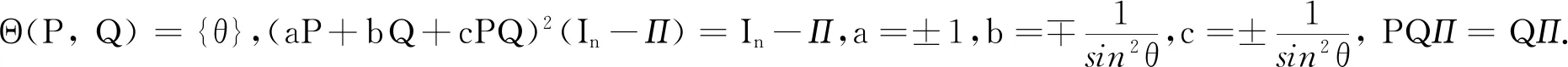
(In-Π)Π=Π(In-Π)=0，

PΠ=U(0⊕R1)U=ΠP，

QΠ=U(0⊕R2)U=ΠQ，

(aP+bQ+cPQ)(In-Π)=

U((aT1+bT2+cT1T2)⊕0)=

(In-Π)(aP+bQ+cPQ)，

则有

(aP+bQ+cPQ)3=

[(aP+bQ+cPQ)(In-Π)+

(aP+bQ+cPQ)Π]3=

(aP+bQ+cPQ)3(In-Π)+

(aPΠ+(b+c)QΠ)3=

(aP+bQ+cPQ)(In-Π)+

a3PΠ+[3a(b+c)2+3a2(b+c)+

(b+c)3]QΠ，

(24)

又因为(a+b+c)∈{-1，1}，a=±1，所以(a+b+c)3=a+b+c，a3=a，从而

3a(b+c)2+3a2(b+c)+(b+c)3=b+c.

结合(24)式，可得

(aP+bQ+cPQ)3=

(aP+bQ+cPQ)(In-Π)+aPΠ+(b+c)QΠ=

aP+bQ+cPQ，

所以aP+bQ+cPQ是三幂等矩阵.类似可证命题ii)～iv)的充分性．

因为aR1+bR2+cR1R2是对合矩阵，所以(21)式中右边的0不出现.结合(18)式和(19)式，进行如下分类讨论.

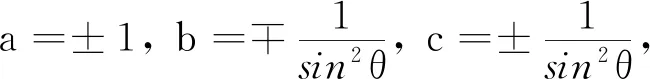
R1=Ix⊕Iy，R2=Ix⊕0.

R1=Ix⊕0，R2=Ix⊕Iz.

c)当x>0，y=0，z=0时，有(a+b+c)2=1，即a+b+c∈{-1，1}.再根据a+b+c的不同取值对(c)进行如下分类.

b2sin2θ-bcos2θ-1=0，

(25)

或

(26)

c2)若a+b+c=1，类似于c1)的证明，可得

(27)

或

(28)

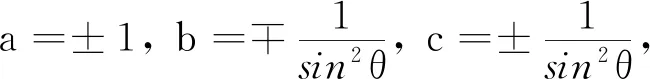
R1=In-2p，R2=0.

R1=0，R2=In-2p.

f)当x=0，y=0，z=0时，R1，R2不存在，此时,

a+b+ccos2θ=0，absin2θ=-1，

P=UT1UH，Q=UT2UH，Π=0.

因此，由a)，d)，(25)式及(26)式可得命题i);由b)，e)，(26)式及(27)式可得命题ii);由f)可得命题iii)．

(In-Π)Π=Π(In-Π)=0，

PΠ=U(0⊕R1)U=ΠP，

QΠ=U(0⊕R2)U=ΠQ，

(aP+bQ+cPQ)(In-Π)=

U((aT1+bT2+cT1T2)⊕0)=

(In-Π)(aP+bQ+cPQ)，

则有

(aP+bQ+cPQ)2=

[(aP+bQ+cPQ)(In-Π)+

(aP+bQ+cPQ)Π]2=

(aP+bQ+cPQ)2(In-Π)+

(aPΠ+(b+c)QΠ)2=

(In-Π)+a2PΠ+[(b+c)2+2a(b+c)]QΠ.

(29)

又因为a+b+c∈{-1，1}，a=±1，所以(a+b+c)2=1，a2=1．

结合(29)式，可得

(aP+bQ+cPQ)2=

(In-Π)+Π+(a+b+c)2QΠ-a2QΠ=In，

从而aP+bQ+cPQ是对合矩阵.类似可证明命题ii)～iii)的充分性．

注记5由定理8 1)中的命题iii)知，aP+bQ是三幂等矩阵的充分必要条件是

Θ(P，Q)={θ}，

(aP+bQ)2(In-Π)=In-Π，

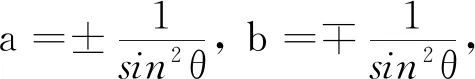
c=0，PΠ=QΠ.

(30)

又因为(30)式等价于

Θ(P，Q)={θ}，

(P-Q)2(In-Π)=sin2θ(In-Π)，

(31)

而(31)式即为文[13]中定理2.11(ii)．

注记6假设c=0，则定理8 1)中的命题i)，ii)不存在，由iv)可以得到iii).由注记5知，此时定理8 1)即为文[13]中定理2.11(ii)．

当c=0时，定理8 2)中的命题i)～ii)不存在，此时aP+bQ是对合矩阵的充分必要条件是

Θ(P，Q)={θ}，(P-Q)2In=sin2θIn，

(32)

此时，(32)式即为文[13]中定理2.11(iii)．