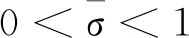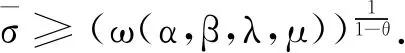四阶两点非齐次边值问题正解的唯一性及对参数依赖性

沈文国，孙建仁，包理群

(1.兰州工业学院基础学科部，兰州 730050;2.兰州工业学院机电工程学院，兰州 730050;3.兰州工业学院电子信息工程学院，兰州 730050)

考察下列四阶两点边值问题正解的存在性与唯一性:

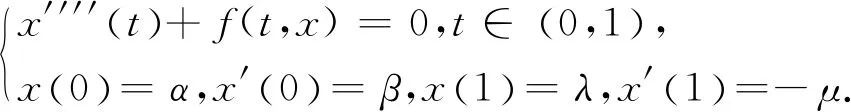
(1)

在材料力学中，问题(1) 表示两端固定的弹性梁的方程.当α=β=λ=μ=0时，许多作者[1-5]采用压缩映象原理、Leray-Schauder不动点定理、锥上的不动点理论等方法研究了问题(1) 正解的存在性.另一方面，近年来许多学者研究了非齐次边值问题[6-13]，其中文[8] 利用单调混合算子理论研究了含两个参数的二阶多点边值问题

(2)

正解的存在性与唯一性.利用与文[8]相似的方法，文[9]研究了一类四阶两点非齐次边值问题存在唯一正解及解对参数的依赖性.利用锥拉伸与压缩不动点定理，Marcos等[10]研究了一类四阶非齐次边值问题的多解性.Korman[14]利用单调迭代方法研究了非线性项满足次线性条件时四阶两点非齐次边值问题(1)正解的存在性问题.Lou[15]利用拓扑度理论和锥理论研究了非线性项满足超线性条件时非齐次四阶两点边值问题 (1)正解的存在性问题．

受文献[8-10]的启发，本文利用单调混合算子理论研究当非线性项满足更一般的条件时四阶两点非齐次边值问题 (1)正解的存在性与唯一性问题.本文假设：

(H1)α>0，β>0，λ>0，μ>0.

(H2)f(t，x)∈C([0，1]×[0，∞)，[0，∞))，且对于x单调递增．

(H3) 存在 0≤θ<1 使得

f(t，kx)≥kθf(t，x)，∀t∈[0，1]，

k∈[0，1]，x∈[0，∞).

(3)

注1本文的主要结论(定理1)是对早期四阶两点非齐次边值问题解的推广及提升，具有一定的理论意义和应用价值.

1 预备知识

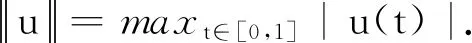
i) 如果一个非空闭凸集P满足：对所有λ≥0，都有λP⊆P成立，并且P∩(-P)={0} (其中0是X中的零元素)，则称P⊆X是一个锥；

ii) 在锥P⊂X上定义一个偏序：x≤y⟺y-x∈P;

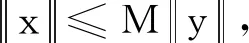
iv) 如果一个锥P的内部P0是非空，则称P是体锥．

定义2[16]假设P是X中的体锥，T:P0→P0.如果对于0≤θ<1，满足

T(kx)≥kθT(x)，∀k∈(0，1)，x∈P0，

(4)

则称T是θ-凹算子.

引理1[16]假设P是实Banach空间X中的正规锥，T:P0→P0是一个θ-凹增算子，则T在P0中存在唯一的不动点.

引理2[15]设 (H1) 成立，对于y∈C[0，1]，则边值问题

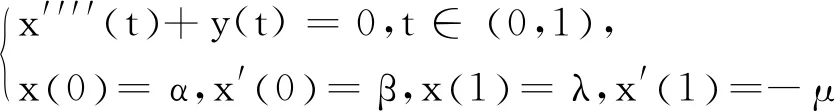
有唯一解

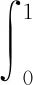
λφ3(t)+μφ4(t)，

(5)

其中，

k(t，s)=

(6)

φ1(t)=(1-t)2(2t+1)，φ2(t)=t(1-t)2，φ3(t)=t2(3-2t)，φ4(t)=t2(1-t).

(7)

引理3[15]假设(H1)成立，则下列结论成立:

i)K(t，s)>0，∀t，s∈(0，1);

ii) φi(t)>0，i=1，2，3，4,t∈[0，1].

注2本文用到如下记号．

i) 假如α，β，λ，μ中之一趋近于∞，记为(α，β，λ，μ)→∞;

ii) 假如α1≥α2，β1≥β2，λ1≥λ2，μ1≥μ2中之一不等式严格成立，记为(α1，β1，λ1，μ1)>(α2，β2，λ2，μ2);

iii) 假如α1≤α2，β1≤β2，λ1≤λ2，μ1≤μ2中之一不等式严格成立，记为(α1，β1，λ1，μ1)<(α2，β2，λ2，μ2);

iv) 假如α→α0，β→β0，λ→λ0，μ→μ0，记为(α，β，λ，μ)→(α0，β0，λ0，μ0).

2 主要定理及证明

定理1假设条件(H1)、(H2)和(H3)成立，则对于任何(α，β，λ，μ)>(α0，β0，λ0，μ0)，问题(1) 存在唯一正解xα，β，λ，μ(t)满足下列结论.

ii)xα，β，λ，μ(t)对于α，β，λ，μ是严格单调递增，即

(α1，β1，λ1，μ1)>(α2，β2，λ2，μ2)>(0，0，0，0)⟹
xα1，β1，λ1，μ1(t)>xα2，β2，λ2，μ2(t)，∀t∈[0，1];

iii)xα，β，λ，μ(t)对于α，β，λ，μ是连续的，即

(α，β，λ，μ)→(α0，β0，λ0，μ0)⟹

证明令X=C[0，1]，P={x∈X:x(t)≥0，t∈[0，1]}，则P是X中的正规锥，且P0={x∈X:x(t)>0，t∈[0，1]}.

对任何(α，β，λ，μ)>(0，0，0，0)，定义Tα，β，λ，μ:P→X如下，

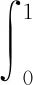
αφ1(t)+βφ2(t)+λφ3(t)+μφ4(t).

(8)

易知，(1)存在一个正解当且仅当算子Tα，β，λ，μ有不动点．

首先证明，Tα，β，λ，μ:P0→P0是一个θ-凹算子.事实上，对于k∈(0，1)，x∈P0,

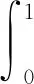
αφ1(t)+βφ2(t)+λφ3(t)+μφ4(t)≥

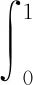
βφ2(t)+λφ3(t)+μφ4(t)≥

kθTα，β，λ，μx(t)，t∈[0，1].

即Tα，β，λ，μ是一个θ-凹算子．

再证明Tα，β，λ，μ:P0→P0是一个增算子.假设对于x，y∈P0并且x≤y，则

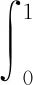
αφ1(t)+βφ2(t)+λφ3(t)+μφ4(t)≤

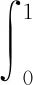
λφ3(t)+μφ4(t)=Tα，β，λ，μy(t)，t∈[0，1].

即Tα，β，λ，μ是一个增算子.因此，由引理1可知算子Tα，β，λ，μ有不动点xα，β，λ，μ∈P0，xα，β，λ，μ是 (1) 的唯一解．

现在来证明xα，β，λ，μ满足定理 1的其他结论．

首先，对于t∈[0，1],

xα，β，λ，μ(t)=Tα，β，λ，μx(t)=

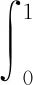
λφ3(t)+μφ4(t)，

结合φi(t)>0，i=1，2，3，4，t∈[0，1]，可知定理1 i) 成立．

假设(α1，β1，λ1，μ1)>(α2，β2，λ2，μ2)>(0，0，0，0)，令

则

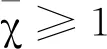
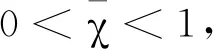
xα1，β1，λ1，μ1(t)=Tα1，β1，λ1，μ1xα1，β1，λ1，μ1(t)≥

xα1，β1，λ1，μ1(t)=Tα1，β1，λ1，μ1xα1，β1，λ1，μ1(t)≥

Tα1，β1，λ1，μ1xα2，β2，λ2，μ2(t)>

Tα2，β2，λ2，μ2xα2，β2，λ2，μ2(t)=

xα2，β2，λ2，μ2(t)，t∈[0，1]，

所以，xα，β，λ，μ(t)在α，β，λ，μ严格递增，即定理1 ii)成立．

对于任给(α0，β0，λ0，μ0)>(0，0，0，0)，首先假设(α，β，λ，μ)→(α0，β0，λ0，μ0)，且

则

xα，β，λ，μ(t)

(9)

令

sup{σ>0:xα，β，λ，μ(t)≥σxα0，β0，λ0，μ0(t),t∈[0,1]}，

xα，β，λ，μ(t)≥σxα0，β0，λ0，μ0(t)，t∈[0，1]，

令

则0<ω(α，β，λ，μ)<1，并且

xα，β，λ，μ(t)=Tα，β，λ，μxα，β，λ，μ(t)≥

(10)

根据 (9)，(10) 可得

又由于当(α，β，λ，μ)→(α0，β0，λ0，μ0)时，ω(α，β，λ，μ)→1 成立，故

(α，β，λ，μ)→(α0，β0，λ0，μ0).

同理，当(α，β，λ，μ)>(α0，β0，λ0，μ0)且(α，β，λ，μ)→(α0，β0，λ0，μ0)时，

因此，定理 1 iii) 成立.定理得证．