激光辐照下卫星筒体部分多物理建模及毁伤效应分析

孙铭远，张昊春，曲博岩，金 亮

（哈尔滨工业大学 能源科学与工程学院，黑龙江 哈尔滨 150001）

引言

激光武器是一种利用定向发射的激光束直接毁伤目标或使之失效的定向能武器，具有准确度高、延迟低、不受电磁干扰等优点[1]。近年来激光武器作为发展最为迅速且已进入实战校验阶段的新概念武器被人们所重视，因此，针对高能激光毁伤效应的研究具有十分重要的意义[2]。

Cai等[3]建立二维轴对称气体动力学模型，模拟了包括逆韧致辐射、热辐射、热传导和对流过程在内的激光能量传递过程。Du等[4]基于有限元法，通过仿真研究了激光功率和扫描速度对粉末床热行为的影响，建立了SLM过程中AlSi10mg熔池温度场的预测模型，并通过实验验证了模型的正确性。Nguyen等[5]使用ANSYS软件，基于有限元分析的方式，模拟了激光辐射下0.5 mm×22 mm密封边缘表面0.2 mm厚胶层的温度场和热流密度，研究介绍了最佳温度、激光束产生的热流密度以及胶粘剂的保持性能。张昊春等[6-7]建立了飞机红外成像仿真模型，求解其蒙皮温度与红外辐射亮度；同时采用建模仿真的方法，基于尾流区海平面温度分布特征，结合三维坐标变换和投影映射方法实现热尾流目标的红外成像仿真过程，得到在相同探测条件下热尾流的辐射能量随波段的分布。Luo等[8]采用有限元法分析了峰值功率密度为50 kw/cm2时，激光光斑速度分别为0 m/s、4 mm/s和10 mm/s时探测器的热效应，基于热传导理论，建立了10.6 mm连续波激光辐照碲化镉探测器的理论模型。李欣荣等[9]使用2种激光器对铝、钢、铜和钛靶材进行烧蚀试验，得到不同材料在不同能量密度下的烧蚀率。郭芳等[10]采用电子束热蒸发方法制备了SiO2薄膜，并在相同实验条件下制备的薄膜加以不同能量的激光辐照，研究在激光辐照前后样片的透射率、折射率、消光系数、膜厚、表面形貌及激光损伤阈值（LIDT）的变化。王刚等[11]利用热弹性理论对CO2激光器辐照K9玻璃材料进行研究，建立激光辐照材料温升及热应力分布二维平面模型，通过解析计算得到由激光辐照半导体材料引起的温度场和应力场的瞬态分布。宋乃秋[12]等建立了典型工况下瞬态一维温度场模型，通过比较分析解来验证数值解的精确性，在此基础上，考虑了相变引起的热导率变化和熔化潜热对温度场分布的影响，求解了相应工况下的温度场分布。此外，Yilbas等[13]针对某些复杂结构件的斜向激光冲击情况，建立了不同冲击角和不同激光偏振状态下的冲击波压力模型。Qiao等[14]采用有限元方法，分析了LSP后表面和深度方向的残余应力分布，建立了不同冲击角和不同激光偏振状态下的冲击波压力模型。Bibhu等[15]通过测量热应变对模型进行了分析验证，研究了扫描速度和激光功率对热残余应力发展的影响。Chen等[16]利用格林函数法和拉普拉斯变换，得到了两种加热方式的温度场和应力场解。Boustie等[17]计算了强激光辐照下靶材产生的反冲冲量以及材料在高速冲击波冲击下产生的破坏效应，进一步确定材料的破坏阈值。

高能激光的实际毁伤过程十分复杂，影响其毁伤效应的因素包括天气状况、跟瞄误差、大气湍流、等离子效应等等[18-19]。考虑各种因素，为获得不同条件和工况下的多物理场，需要大量的实验测量数据，工作量比较大，成本高，且很难在某一外部条件下进行重复实验。通过数值模拟的方法对卫星筒体部分的毁伤效应进行分析，可以极大地降低研究成本，对实际实验过程有一定的指导作用。本文基于Fourier的非稳态导热方程，对典型工况激光辐照下卫星筒体的毁伤过程进行了数值模拟，获得了不同功率下靶材的温度场和应力场分布，研究了靶材的熔化曲线及应力耦合效应。

1 激光辐照下卫星筒体的数学模型

高功率激光在发射后经过大气耗散、湍流效应、等离子效应等多种作用的衰减后，辐射到人造卫星上，同时由于靶材内部的热传导及自身高温特性的影响，形成了不均匀的温度场和应力场。靶材的大致结构和毁伤的具体情况可参考图1所示。

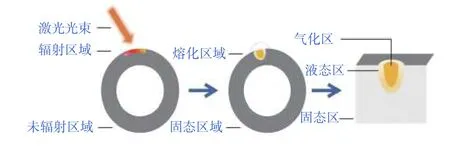
图1 激光辐射下筒体靶材毁伤过程示意图Fig.1 Schematic diagram of damage process of cylinder target under laser irradiation

当激光辐射到靶材表面时，一部分激光被反射，另一部分激光则被靶材吸收，随着激光辐射过程的进行，目标表面的温度不断升高，导致目标熔化，甚至汽化，最终达到毁伤靶材的作用。激光毁伤人造卫星的过程涉及了激光与靶材之间复杂的物理和化学反应，为了便于建模分析，做如下假设：

1）假设在激光辐射过程中，靶材的热物性及光学特性不随温度升高而改变；

2）忽略靶材与周围环境的热交换作用；

3）假设激光的功率密度在其辐射区域分布均匀：

4）假设激光光斑直径d0远大于板厚L，远小于热扩散长度。

激光在辐射靶材的过程中，靶材表面不断吸收热量，其吸收的热量又会以热传导的形式传递到靶材内部，进而形成温度场。为了获得靶材温度场的数学模型表达式，必须根据能量守恒方程和傅里叶定律来建立导热微分方程：

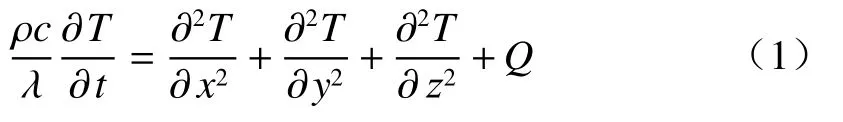
式中：ρ表示密度，单位kg/m3；c表示比热容，单位kJ/（kg·K）；λ表示导热系数，单位kW/（m·K）；Q表示其他源项。人造卫星在遥远的太空中，其初始温度随其位置不断变化，但激光毁伤所需的时间非常短，因此可以认为靶材在激光辐射过程中其温度和热边界条件是不变的。其初始条件和边界条件为

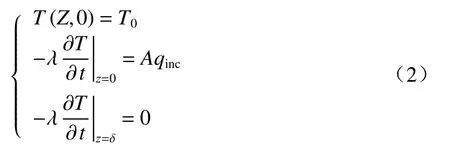
为了对靶材各位置的温度进行求解，需要对网格进行离散化划分。现将网格划分为均匀的n个子区域，其中各子区域长度为Δx，各节点之间距离为δx，这里取Δx=δx=h（空间步长）。那么其内部节点、左右边界与相邻节点之间的关系可表示为

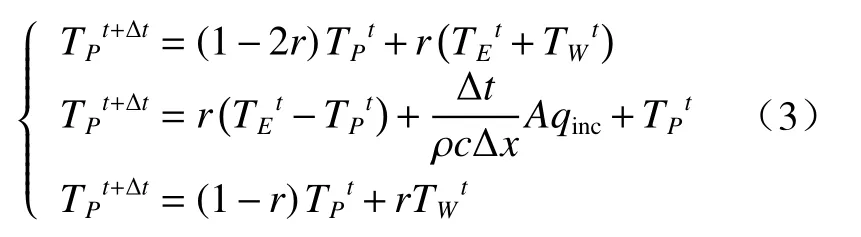
式中：P为所研究的控制节点；W为左节点；E为右节点；r为网格比，反应了网格的质量，Δt和Δx分别为每次计算的时间和空间步长；ρ和c分别是靶材的密度和比热容；A为靶材表面的吸收系数；qinc表示辐照目标表面的激光功率密度。

（3）式为推导的边界迭代方程，其截断误差均为0（Δx），对于内部节点的迭代方程，其截断误差均为0（Δx2），这对提高运算精度是十分不利的。为保证整个网格的截断误差一致，在左右边界各设一个虚点，即在左边界处设i=0的节点，在右边界处设i=n+1的节点。这时左右边界迭代方程的截断误差为0（Δx2），与中间节点相同。对于整个网格来说，其中各节点截断误差都为0（Δx2），保证了运算的精度和稳定性。

那么内部节点、左右边界与相邻节点之间的关系可改进为

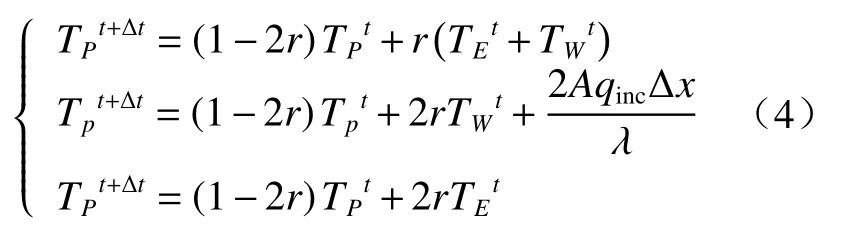
根据（4）式中各节点的温度关系，在给定具体边界初始条件后，便可以获得最基本的温度场分布。但激光在实际毁伤过程中，靶材温度往往会在极短的时间内达到其熔点，甚至汽化温度。在前面温度场分析的过程中，并没有考虑熔化和汽化潜热，以及熔化前后导热系数变化的影响，这些复杂情况将会在使用编程时分别考虑计算，具体流程图如图2所示。

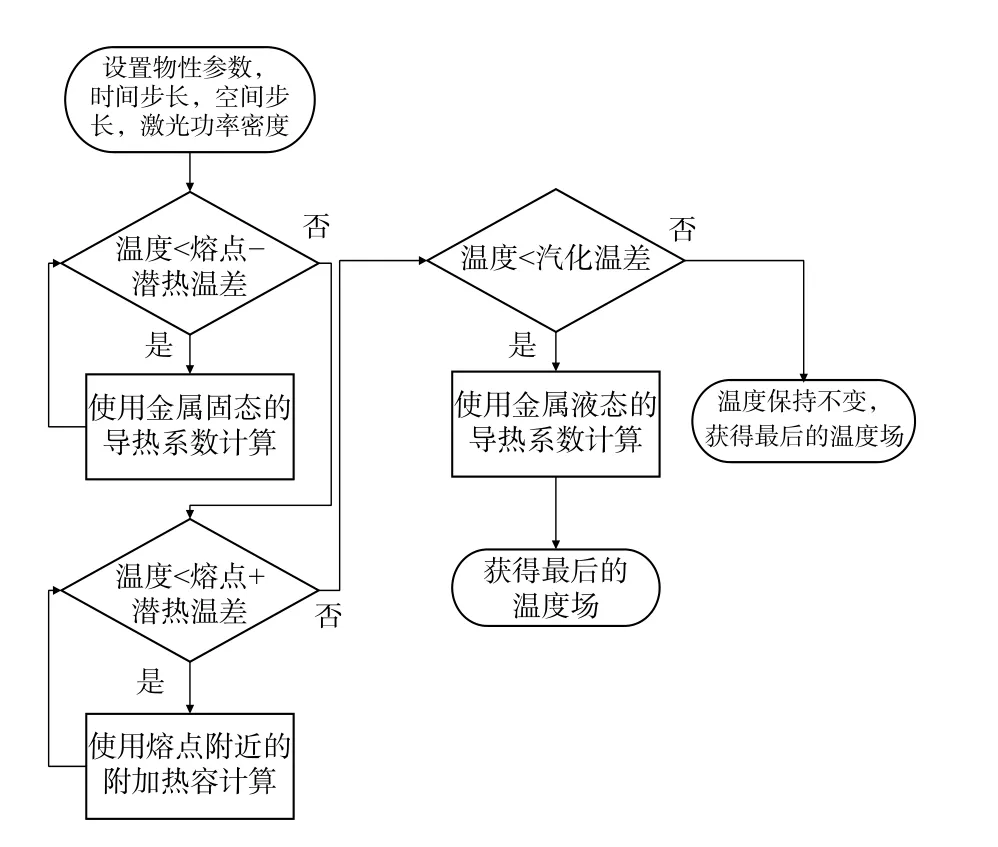
图2 靶材的温度场计算流程图Fig.2 Flow chart of target temperature field calculation

薄壳圆柱体作为人造卫星主体的一种常见结构类型，在激光辐射的过程中，圆柱表面会对靶材的吸收功率产生一定衰减作用，建立的激光辐射圆柱模型如图3和图4所示。

图3和图4分别为两组坐标系，其中图3是以柱心为原点的中心坐标系，θ为激光光轴与圆筒轴之间的夹角。图4是以柱面上激光辐射中心为原点的柱面坐标系，X2、Y2（环向距离）坐标轴在圆筒外表面，设β为XY平面离开X2轴角度，则β=D/R。

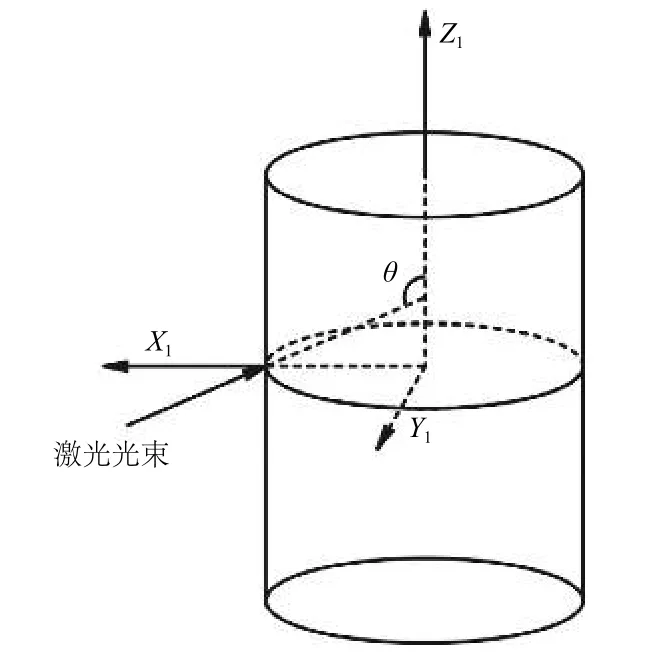
图3 中心坐标系Fig.3 Central coordinate system

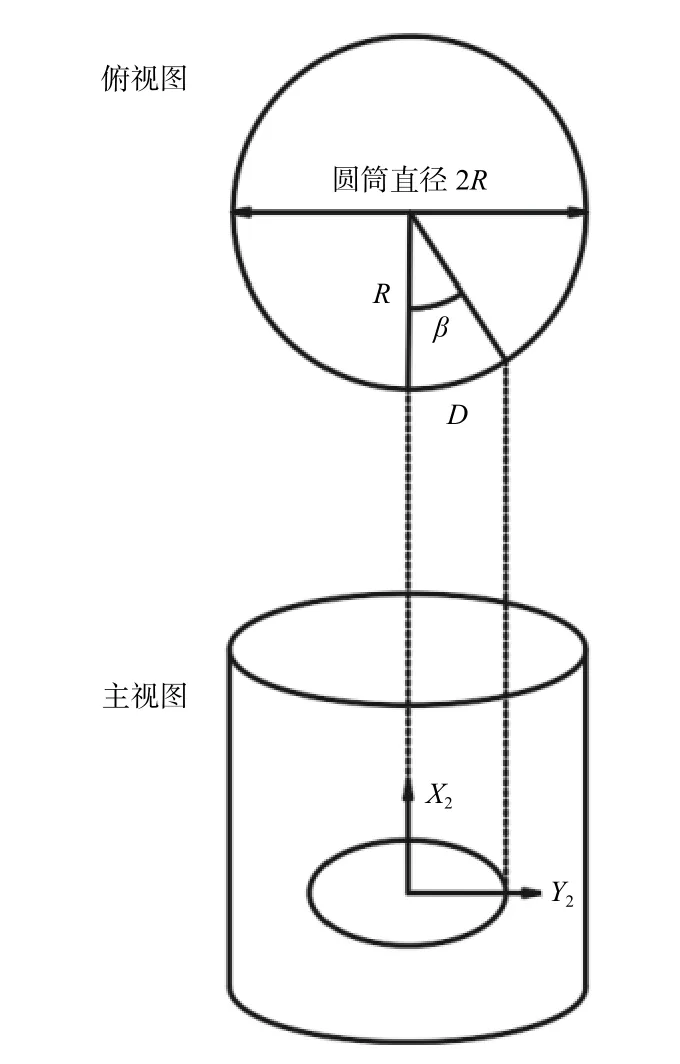
图4 柱面坐标系Fig.4 Cylindrical coordinate system

于是圆筒壳表面的入射激光功率可表示为

式中：θ为激光光轴与圆筒轴之间的夹角（rad）；β为XY平面离开X2轴角度（rad）；Q0为入射的激光功率（W/m2）；Qy为筒体结构靶材表面实际吸收的激光功率（W/m2）。

靶材经过激光辐射后形成温度场，又由于温度场温度分布不均匀形成应力场。假设圆筒壳体两端自由且绝热，筒内无内热源，对于圆筒壳结构，在无外部载荷时可以不考虑切向应力。利用边界条件、温度场求得积分常数，那么由于温差引起的热应力在壁厚方向的分布为[20]

总应力为

式中：σr为径向应力（MPa）；σθ为环向应力（MPa）；σz为轴向应力（MPa）；α为热膨胀系数（℃-1）；E为弹性模量（GPa）；a为圆筒内径（m）；b为圆筒外径（m）；r为圆筒所求位置处半径（m）；D1，D2为积分常数；υ为泊松比；ΔT为内外壁温差（℃）。

2 典型工况下靶材的多物理场分布及毁伤效应分析

2.1 靶材温度场的建模与计算

Al及其合金广泛应用于人造卫星的制造中。现取Al作为靶材来进行温度场的计算，其热物性参数如表1[21]所示。由于金属熔化前后导热系数发生了变化，所以网比r也发生了变化，但变化前后都应满足0≤r≤0.5。考虑到r可能取最大值，设空间步长Δx=0.1 cm，Δt=0.005 s，数值法计算工况分别取材料厚度d=2 cm，激光辐射时间tf=1.5 s，迭代次数n=300次。金属材料的吸收系数与激光的波长等因素有关，对于表面光滑保存良好的铝材，若激光波长为1.315 μm时，靶材表面的吸收系数在0.1～0.2之间，铝的表面吸收系数A=0.2，辐射到靶材的激光功率密度为10 kW/cm2，则可计算得到一维温度场随时间和空间变化的数值解，人造卫星外壳的温度场分布如图5所示。

表1 铝的热物性参数Table 1 Thermophysical property parameters of aluminum

从图5可看出，在初始阶段靶材的温度场各位置温度平稳上升，在达到熔化温度时由于相变潜热的影响，温度将在一定的时间内维持在600 ℃左右，之后由于熔化前后靶材导热系数发生了变化，靶材温度的上升速率有了明显的提升。同时还可以看出，在毁伤时间内，靶材底部温度并未超出其熔化温度，因此靶材并未因温度过高而发生损毁。

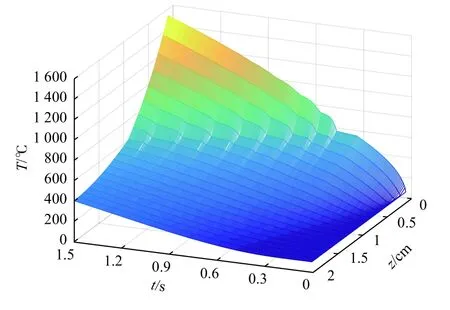
图5 靶材的温度场分布Fig.5 Temperature field distribution of target

为了研究激光功率密度对靶材温度场的影响，在保证其他条件一致的情况下，分别取激光的功率密度为8 kW/cm2、10 kW/cm2、12 kW/cm2、15 kW/cm2，讨论靶材表面温度在不同激光功率密度下温度随时间变化的差异，具体情况如图6所示。

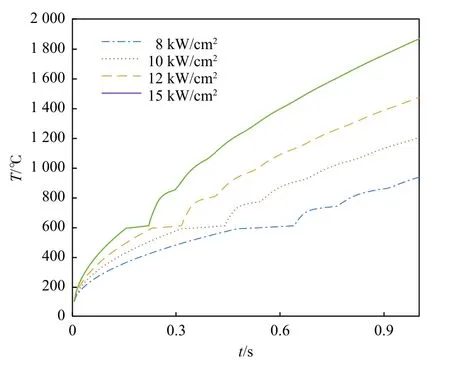
图6 不同功率密度下靶材表面温度分布Fig.6 Surface temperature distribution of target at different power densities

随着激光功率密度的升高，金属达到相变点温度后，激光在相变点处停留的时间不断减小，同时随着激光功率密度的升高，曲线的斜率（温升速率）也不断升高，靶材达到相变点所需时间不断减少。这是由于相同金属从一定温度到完全融化过程中，所需热量是一定的，激光功率密度不断升高，靶材表面单位时间吸收的热量也随之升高，故金属毁伤过程所需的时间更短。

为了更直观地反映靶材毁伤速率与激光功率密度的关系，本文取激光辐照下达到或超过靶材熔点的材料最大深度作为靶材毁伤深度。在所得温度场的基础上获得靶材的毁伤深度曲线，如图7所示。从图7可以看出，相较于靶材的温度分布，该曲线对激光功率的敏感性并不明显，因此，这里取激光功率密度分别为10 kW/cm2、20 kW/cm2、40 kW/cm2、80 kW/cm2进行对比分析。

图7 不同功率密度激光的击穿曲线Fig.7 Breakdown curves of lasers with different powerdensities

由图7可看出，在相同时间内，随着激光功率密度的不断增大，靶材的毁伤深度也随之增加。曲线的斜率为靶材的毁伤速率，可以看出高功率的激光在初始时刻毁伤速率高，随着毁伤效应的不断进行，各功率的毁伤速率趋近相同。当激光功率密度一定时，随着时间的增加靶材毁伤速率在某一时间内会有所降低，随后基本保持不变，约为10 cm/s。这是由于激光在毁伤过程中表层金属发生汽化现象所影响。

2.2 靶材应力场的建模与计算

为了获得靶材的应力场分布，在（6）式的基础上，需要知道靶材的力学性能参数和靶材的内外壁温差，这里仍以铝作为基体材料，其参数可通过查表获得，如表2所示。靶材的内外壁温差可以根据前面获得的温度场数据得出，如表3所示。

表2 铝的力学性能参数[21]Table 2 Mechanical property parameters of aluminum

表3给出了激光功率密度为20 kW/cm2时靶材的内外表面温差。其分布规律与外壁面温度相似，这是由于内壁面相比于外壁面温度变化并不明显，从而导致了内外表面温差随时间不断变大。根据（6）式，表2和表3的壁面温差对圆筒壁面的径向应力、环向应力和轴向应力进行计算，以铝的热物性参数和力学性能参数作为基本参数，整理可得3个方向分应力及总应力随时间和空间的变化趋势，如图8～图11所示。

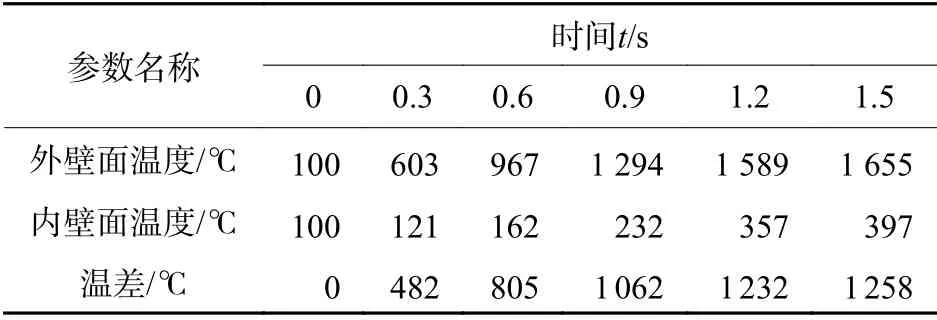
表3 靶材的部分内外壁温差数据Table 3 Partial inner and outer surface temperature difference data of targets

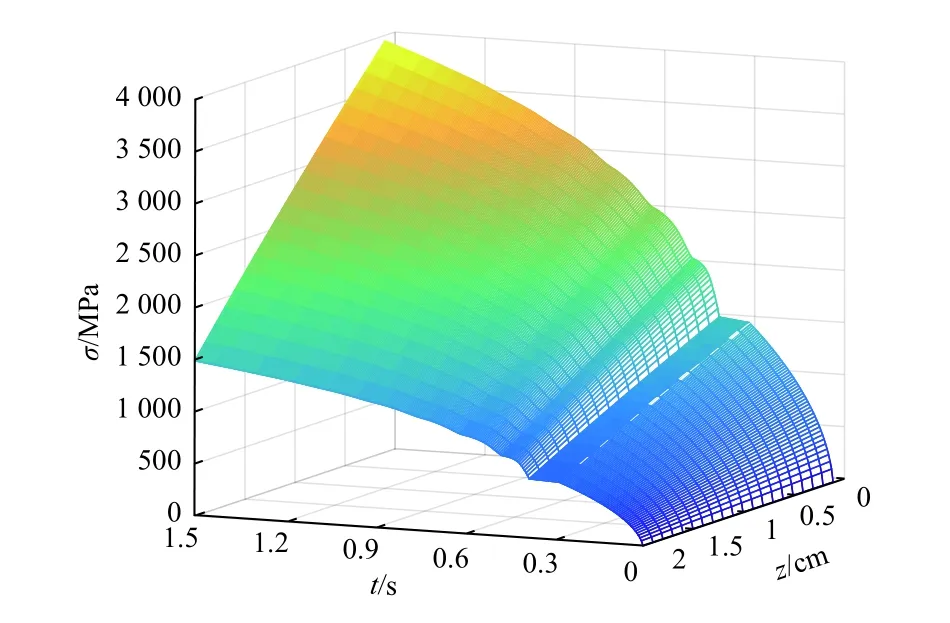
图8 靶材径向应力分布Fig.8 Target radial stress distribution

由图8可知，在相同时间内，靶材沿厚度方向径向应力逐渐减小，呈近似线性关系，在靶材底层处径向应力达到最小值。同时，径向应力的大小明显受温差曲线的影响，整体应力在1 000 MPa～2 000 MPa之间，应力在一段时间内保持不变，有明显的停顿。

图9为靶材的环向应力沿壁厚方向随时间的变化情况。其分布规律与径向应力近似相同，靶材沿厚度方向径向应力逐渐减小，在靶材底层处达到最小值，呈近似线性关系。

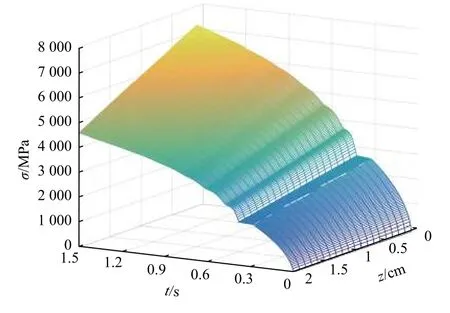
图9 靶材环向应力分布Fig.9 Target hoop stress distribution

图10为靶材的轴向应力沿壁厚方向随时间的变化情况。与径向和环向应力不同，靶材的轴向应力沿壁厚方向逐渐增大，靶材表面轴向应力近似为零，近视成锥型，而应力在靶材底层处达到最大值，且靶材的轴向应力大小明显要比径向和环向应力小得多，仅为几百MPa。

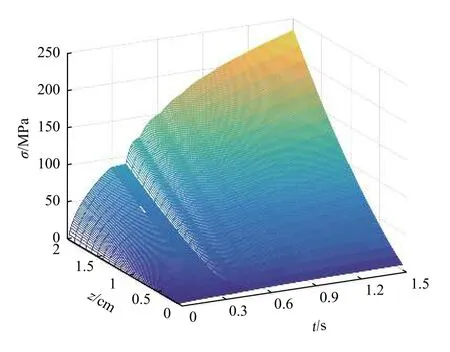
图10 靶材轴向应力分布Fig.10 Target axial stress distribution

对3个应力进行矢量求和，可以得到靶材沿壁厚方向随时间的变化情况，如图11所示。靶材的总应力分布，明显受径向与环向应力分布的影响，其分布规律也近似相同，在靶材内部温度达到熔点处，其应力大小也出现短暂停顿现象，随后应力迅速升高，直至超出靶材许用应力大小，进而发生损毁。

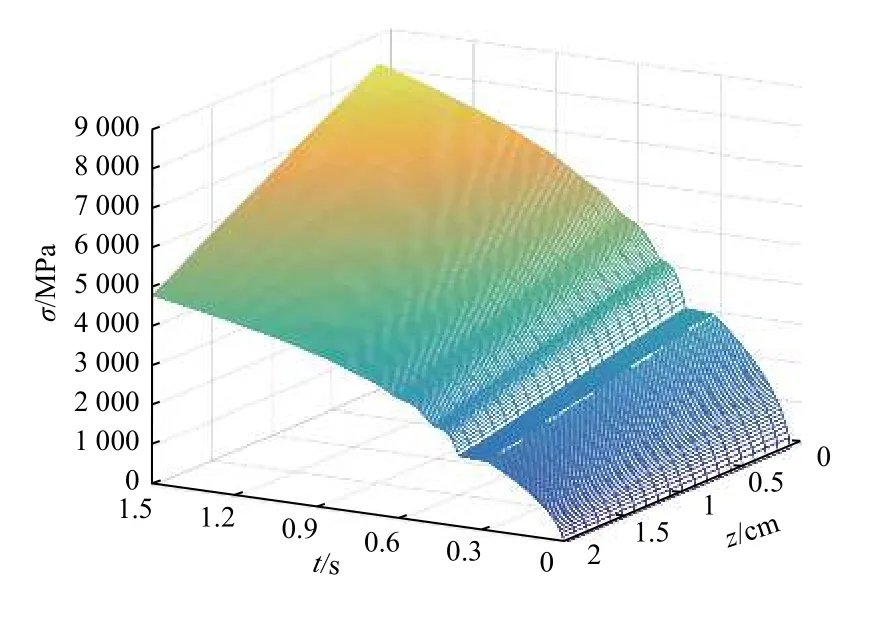
图11 靶材总应力分布Fig.11 Target total stress distribution

靶材总应力相同条件下，在靶材表面处最大，也是最容易超出许用应力的位置。同时，靶材由于应力耦合效应，其内部许用应力也随时间不断下降，如表4所示。为了更加直观地从应力角度对激光的毁伤效应进行分析，取靶材表面处总应力与许用应力进行分析，靶材表面总应力和许用应力随时间的变化曲线如图12所示。

表4 Al的许用应力[20]Table 4 Allowable stress of Al

从图12可以看出，靶材在强激光的辐照下表面温度不断升高，受到的总应力也在不断变大，但其许用应力却在不断降低。在0.003 s左右靶材表面的总应力已经大于许用应力，此时靶材的安全性已经无法保证，随时可能发生力学破坏。

图12 靶材表面总应力和许用应力分布Fig.12 Target surface total stress and allowable stress distribution

3 结论

本文建立了激光辐照下卫星圆型筒体的计算模型，实现了靶材的温度场、应力场建模仿真，研究了激光不同功率密度对毁伤效果的影响，得出如下结论：

1）建立了激光辐射下各节点之间的迭代方程，结合初始条件和边界条件，建立了卫星的温度场模型。在此基础上考虑了靶材的熔化和汽化现象，对温度场进一步进行完善。最后基于所得温度场，获得了靶材的熔化速率及位移曲线，可以从温度方面对激光毁伤效应进行评估。随着激光功率密度的不断增加，初始时刻靶材的毁伤速率也在不断增加，然而随着毁伤过程的不断进行，到达相变处其熔化速率趋于稳定，约为10 cm/s。

2）建立了激光辐射下卫星的应力场模型。在应力场建模计算中结合卫星结构，从圆筒结构出发进行应力场的建模计算，并考虑应力耦合效应，分析靶材的毁伤效果，从应力方面对激光的毁伤效应进行评估。在典型工况下，靶材内部应力在0.003 s时便超出了许用应力，其安全性能无法保证。