CR1500HF热成形钢U形件不同位置的高速拉伸性能及其有限元模拟

刘培星

(山东钢铁集团日照有限公司钢铁研究院，日照 276800)

0 引 言

汽车轻量化是降低能源消耗、减少温室气体排放的重要途径。1.5 GPa热成形钢(超高强钢)是汽车轻量化的重要材料，已广泛应用于如门内防撞梁、保险杠、中通道以及A，B，C柱等车身安全结构件[1-3]。热成形零部件一般采用热成形淬火工艺制造,加热至奥氏体化的板料在高温成形后的保压过程中快速冷却，显微组织由奥氏体转变为马氏体，从而获得极高强度。板料在高温状态下的成形性能较好，零部件回弹小[4]。

在整车开发设计过程中采用有限元方法(FEM)进行计算机辅助工程(CAE)碰撞仿真，可以降低汽车开发成本，缩短车型开发周期。CAE仿真所用材料卡片的准确性直接关系到有限元仿真结果的准确性。材料动态力学性能试验可以为有限元碰撞仿真分析提供基础材料参数；不同应变速率下的屈服强度、流变应力、抗拉强度和延伸率等是车身安全重点关注的性能[5]。国内外车用材料高速拉伸性能的相关研究很多，内容包括检测试验设备、检测方法[6]、本构方程[7-8]等；但目前大多是原材料的高速拉伸性能研究。服役过程是零部件的碰撞安全服役过程，需考虑从零部件取样进行分析。

为此，作者在1.5 GPa级热成形钢U形件不同位置取样进行高速拉伸试验，对比分析了不同位置的拉伸性能以及应变速率对拉伸性能的影响，采用combined S-H模型对真应力-真塑性应变曲线进行拟合延伸；构建材料高速拉伸有限元模型，模拟了材料的高速拉伸行为及夹持端应力分布，拟为热成形钢在车身中的碰撞安全设计与分析提供基础数据和技术支撑。

1 试样制备与试验方法

试验材料为山东钢铁集团有限公司生产的1.5 mm厚CR1500HF热成形钢，主要化学成分(质量分数/%)为0.24C，0.26Si，1.25Mn，0.003 3B，0.19Cr，0.03Ti。采用200T热成形系统制备热压淬火U形零部件(形状和尺寸见图1)，加热温度为930 ℃，保温时间为5 min，压力为20 MPa，保压时间为10 s。为了进行对比，采用冷冲压成形工艺制备相同尺寸U形零部件，压力为20 MPa，保压时间为10 s。

图1 U形件的截面尺寸和整体形状

在U形零部件的法兰、侧壁和底部3个位置取样，制成如图2所示的高速拉伸试样。采用HTM5020型高速拉伸试验机进行拉伸试验，应变速率分别为1，10，100，200，500 s-1，各做3次试验取平均值。拉伸过程中当应变速率大于100 s-1时，通过应变片采集拉伸应力；实际拉伸前先进行预拉伸试验，在弹性段受力范围内标定应变片。

图2 高速拉伸试样尺寸

2 U形件拉伸性能分析

2.1 热压成形与冷冲压成形件拉伸性能对比

由图3(a)可以看出，冷冲压成形U形件不同位置的抗拉强度相差不大，但侧壁位置的屈服强度相比于法兰和底部位置提高约40 MPa。这是由于冷冲压成形过程中零部件在侧壁位置发生塑性变形导致的。因此，冷冲压成形零部件在进行碰撞分析时需要考虑部分区域塑性变形导致的性能不均的影响。由图3(b)可以看出，热压成形U形件法兰和底部位置的拉伸性能比较均匀，但侧壁位置的屈服强度和抗拉强度相比于法兰和底部位置均降低约100 MPa。这是由于在热压成形过程中侧壁位置发生减薄，模具与板料之间间隙增大，板料冷却不足导致的[9]。因此，热压成形零部件在进行碰撞分析时需要考虑部分位置因冷却不足导致强度降低的影响。

图3 冷冲压成形和热压成形U形件不同位置的拉伸性能(应变速率1 s-1)

2.2 热压成形件的高速拉伸性能

由图4(a)和图4(b)可以看出，随着应变速率的增加，U形件法兰位置的屈服强度和抗拉强度增大，而断后伸长率先下降再增大后又降低，未表现出明显的规律性。

图4 热压成形U形件法兰位置在不同应变速率下的拉伸性能

不考虑颈缩和断裂过程，对试验获取的工程应力-应变曲线进行数据处理，获得真应力-真塑性应变曲线，见图5(a)；采用combined S-H模型(Swift和Hockett-Sherby模型)拟合延伸图5(a)中的真应力-真塑性应变曲线(95%置信度条件)，延伸至应变为1处，结果见图5(b)。combined S-H模型表达式为

图5 试验得到不同应变速率下的真应力-真塑性应变曲线及经combined S-H模型拟合延伸后的曲线

σ=(1-α)[C(εpl+ε0)m]+

(1)

式中：σ为真应力；α为组合因子；εpl为真塑性应变；σsat为拟合曲线的屈服极限；σi为拟合曲线初始流变应力；C，ε0，m，p为常数。

3 拉伸有限元建模及结果

3.1 模型建立及条件设置

根据实际几何尺寸建立高速拉伸有限元模型，选择壳单元(*SECTION_SHELL)进行网格划分，网格和边界条件设置见图6，通过控制不同“位移VS时间”实现不同应变速率拉伸仿真。采用“*MAT24”号材料卡片(Cowper-Symonds本构模型)，将图5(a)中不同应变速率下的真应力-真塑性应变输入卡片中进行模拟，试验材料的弹性模量为2.07×1011MPa，密度为7 830 kg·m-3，泊松比为0.28，屈服强度为1 147.2 MPa。

图6 高速拉伸试样有限元网格划分和边界条件

为简化计算，对物理模型作如下假设：1)拉伸过程中试样变形速率恒定，忽略实际拉伸过程中速率降低对拉伸性能的影响；2)弹性段变形可完美恢复，忽略弹性段标定过程对后续拉伸性能的影响；3)弹性模量为恒定值，忽略应变速率对弹性模量的影响。

3.2 有限元模拟结果及验证

采用建立的有限元模型计算应变速率分别为1，500 s-1下的真应力-真塑性应变曲线，并与经combined S-H模型延伸的试验结果进行对比。由图7(a)可以看出，有限元计算结果与试验结果具有较好的一致性，应变速率为1，500 s-1下真应力的均方根误差分别为19.98,39.48 MPa。由图7(b)可见，在高速拉伸过程中拉伸试样夹持端虽然大部分都处于弹性段(如位置A～F)，但不同位置的受力状态不同，位置D，E，F处的等效应力变化曲线重合。由此判断，该拉伸试样上应变片粘贴位置距离试样圆弧的距离至少应大于14 mm，建议大于19 mm。

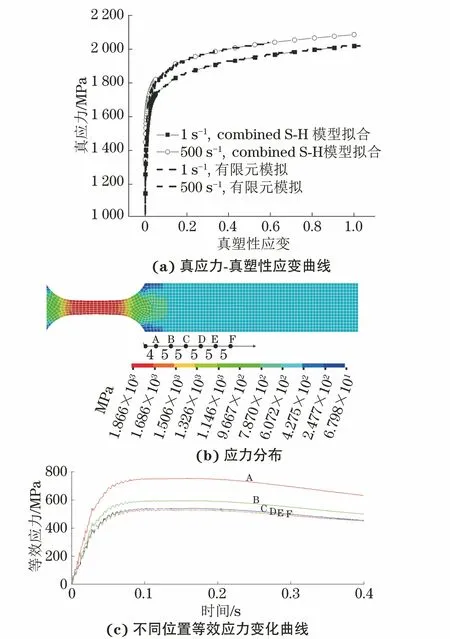
图7 高速拉伸过程中真应力-真塑性应变曲线和夹持端应力有限元分析结果

4 结 论

(1)CR1500HF钢冷冲压成形U形件不同位置抗拉强度相差不大，但侧壁位置的屈服强度略高于法兰和底部位置，冷冲压成形件在进行碰撞分析时需考虑部分区域塑性变形导致的性能不均的影响；热成形U形件侧壁的屈服强度和抗拉强度低于法兰和底部位置，在进行碰撞分析时需要考虑部分位置因冷却不足强度降低的影响。

(2)随着应变速率的增加，热压成形U形件不同位置的屈服强度和抗拉强度均增大，即CR1500HF钢具有一定的应变速率强化效应。

(3)由高速拉伸有限元模型模拟得到的真应力-真塑性应变曲线与combined S-H材料本构模型拟合延伸得到的真应力-真塑性应变曲线吻合较好，应变速率1，500 s-1的均方根误差分别为19.98，39.48 MPa；有限元模拟得到高速拉伸过程中拉伸试样夹持端大部分处于弹性变形阶段，应变片粘贴位置距试样圆弧处距离应大于19 mm。