基于深度学习的中心回线瞬变电磁全区视电阻率计算

吴国培，张莹莹，张博文，赵华亮

(新疆大学 地质与矿业工程学院，新疆 乌鲁木齐 830047)

0 引言

瞬变电磁法(TEM)是一种时间域的电磁探测方法，在水文、工程、环境等探测领域得到广泛应用[1-4],全区视电阻率能快速直观反映地下地层的电性变化，目前在实际资料解释中应用广泛。由于电阻率参数与瞬变响应之间存在复杂的隐函数关系[5]，直接用解析式求解视电阻率存在一定困难。前人对视电阻率的计算做了一些研究：苏朱刘等[6]提出了一种虚拟全区视电阻率，能相对反映地下电性层电阻率的变化规律；白登海等[7]借助瞬变场参数，分别迭代求取早期、晚期视电阻率的精确值,进而通过转折点构成一条完整的全区视电阻率曲线；熊彬等[8]使用逆样条插值的方法，以归一化感应电动势的极值点为界，分段用逆样条插值求解非线性方程的根，进而求出全区视电阻率；陈清礼等[9]根据二分搜索算法，找到感应电动势与视电阻率单调下降的区间，利用二分法直接求解全区视电阻率；武军杰等[10]计算了分量视电阻率，为回线瞬变电磁法多个分量综合解释提供必要的基础；郝延松等[11]对回线源瞬变电磁视电阻率计算方法进行讨论，用磁场定义全区视电阻率不存在双解问题，但现在通用的野外仪器测量感应电动势较为方便。

人工神经网络(artificial neural network,ANN)反演是模拟人脑机理和功能的一种新型计算机和人工智能技术，只需经过适当的学习训练就能够解决复杂的实际问题，具有广阔的发展前景[12]。在瞬变电磁视电阻率求解方面已取得了一些研究进展，谢林涛等[13]使用感应电压对电流的归一化值与视电阻率值构建ANN快速求解视电阻率；谢品芳等[14]根据含时间的核函数、磁场与瞬变场参数之间的关系，构建ANN求解视电阻率。

2006年，Hinton等[15]在《科学》首次提出深度学习，现已成为人工智能的一个研究热点。深度神经网络(DNN，deep neural network)模型相较于浅层模型(ANN)对非线性函数有更好的表示能力[16]，同时具有很高的容错性、 鲁棒性及自组织性[17]。目前,结合深度学习解决瞬变电磁相关问题的研究还较少，将其引入用于瞬变电磁视电阻率计算。本文以均匀半空间中心回线瞬变电磁的解析式为基础，将其与深度学习结合，构建归一化感应电动势F(u)为输入，瞬变场参数u为输出的DNN模型。训练算法选择Nadam算法[18]，该算法自适应能力强，具有预更新能力，能够加速DNN训练过程。将训练好的DNN模型进行保存，不需要通过大量迭代，只需将归一化感应电动势值代入保存好的模型，就能快速计算视电阻率。通过仿真实验及实测资料的处理，验证了该方法的实际运用效果。

1 中心回线瞬变电磁视电阻率求解

1.1 瞬变电磁视电阻率基本求解理论

瞬变电磁中心回线装置下的瞬变电磁测深，在地下为均匀介质的情况下，采用的阶跃电流脉冲函数为

(1)

电磁场存在如下解析解[19]：

(2)

(3)

(4)

结合式(2)及式(4)进行化简，可得：

(5)

式中：ρ为均匀半空间电阻率；a为发射回线半径；u为瞬变场参数；erf(u)称为概率积分；t为供电流关断后的延迟时间；μ0为均匀半空间的磁导率(一般取真空中的磁导率，μ0=4π×10-7H/m)。

1.2 视电阻率双值问题的讨论

实际工作中，感应电动势可以由仪器测出，则将式(5)进行化简，等式右侧均为已知量，左侧为只含有瞬变场参数u的形式，令F(u)等于等式的左侧，可得：

(6)

F(u)也被称为归一化感应电动势[8]。

图1给出了归一化感应电动势F(u)与瞬变场参数u之间的函数关系。通过计算可知：u=1.613 6时，F(u)存在极大值0.701 6。在实际应用中，式(4)可以方便地计算出归一化感应电动势的值，再根据式(6)即可计算出瞬变参数u。视电阻率与瞬变场参数u满足

(7)

通过式(7)可计算出全区视电阻率，由此求解视电阻率关键的部分转化为求解式(6)。式(6)中含有概率积分，直接求解瞬变电磁场反函数存在一定困难，且根据图1，给定一个归一化感应电动势的值F(u)，计算出的瞬变场参数u有2个解。

图1 F(u)与瞬变场参数u的变化特征Fig.1 F(u) and the change characteristics of the transient field parameter u

对于视电阻率的双值问题，本文以瞬变场参数u=1.613 6为界，构建2个以归一化感应电动势F(u)为输入，瞬变场参数u为输出的DNN模型，并对瞬变场参数u另一区间最大值进行确定。据式(4)，瞬变场参数u与发射回线边长呈正比，与延时、电阻率呈反比。发射回线边长取野外常用的大回线边长600 m[20]，延时取接收机最小延时3×10-6s[21]，不同地质年代各种岩石电阻率的变化范围在[1,100 000]Ω·m[22]，电阻率取其最小值1 Ω·m，计算出瞬变场参数u为194，以此确定瞬变场参数u的范围为(0,194]。则第一个DNN模型瞬变场参数u的区间为(0，1.613 6]，第二个DNN模型瞬变场参数u的取值为(1.613 6,194]。

对所构建的2个DNN模型，发射回线边长取100 m，作出DNN视电阻率选取判别图，如图2所示。图中横、纵坐标的取值覆盖了多数岩石电阻率及市面上大多数接收机的延时范围。由图可得，第一个DNN模型比第二个DNN模型能够计算视电阻率的区域面积大很多。实际工作时，可根据发射回线边长、仪器延时范围并结合工区岩石电阻率的大致范围，确定选用哪个DNN模型进行计算。

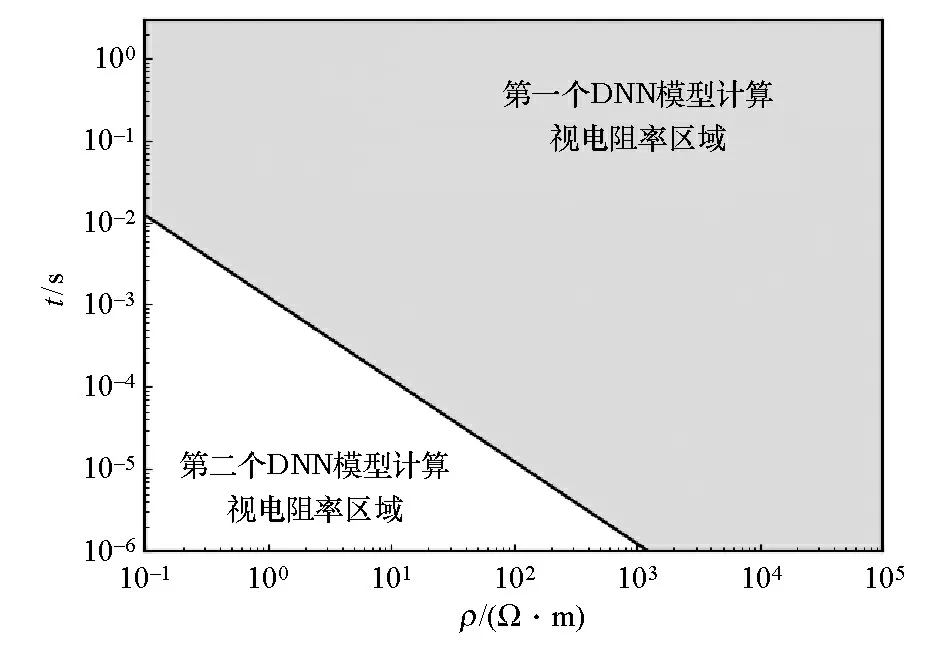
图2 DNN计算视电阻率选取判别Fig.2 DNN calculation of apparent resistivity selectiondiscriminant diagram

在计算出视电阻率后，借助M.N.Nabighian[23]的烟圈扩散理论，根据

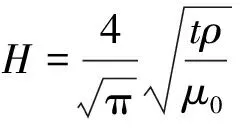
(8)

计算出视电阻率ρ所对应的视深度H,绘制视电阻率与视深度断面图进行快速成像解释。

2 深度学习的设计与实现

2.1 深度学习原理

深度学习属于机器学习的一种。对于传统程序设计，是已知数据与制定的规则，进而求出答案，而机器学习则是已知数据与答案，通过机器学习找到它们之间所对应的规则，深度学习的训练过程就相当于找到对应规则的过程。这些规则随后可应用于新的数据，并使计算机自主生成答案[24]。深度学习是基于误差反向传播算法，学习的过程由信号的正向传播与误差的反向传播两个过程组成，其结构一般包含输入层、隐含层、输出层三部分。深度学习的核心在于存在多个隐含层。通用5层DNN结构如图3[25]所示，各层中的空心圆代表神经元。

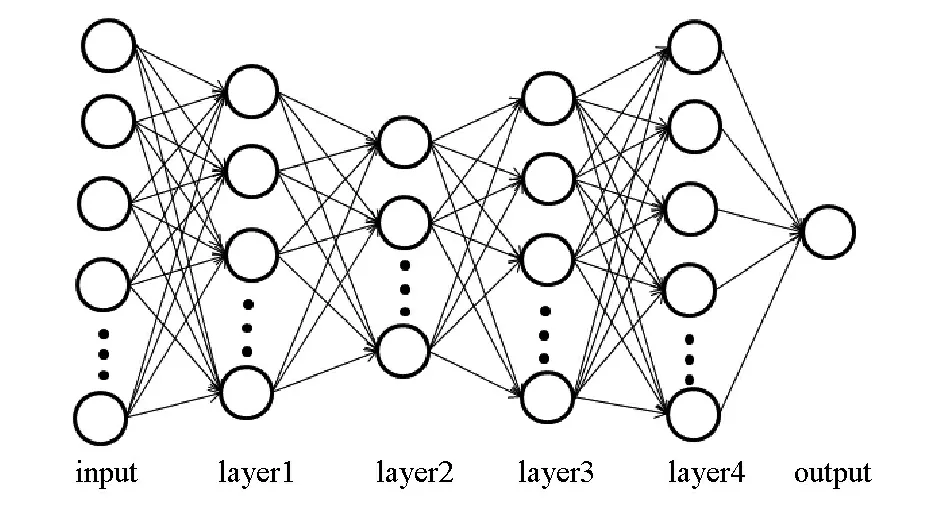
图3 通用5层DNN结构[23]Fig.3 Universal five layer DNN structure

具体的学习过程为：正向传播时，样本从输入层传入，输入层的值在激活函数的传递下，经各隐含层处理后，最终到达输出层。Sigmoid激活函数表达式为[26]：

(9)

式中:p为前一层神经元的值，f(p)为传递到下一层神经元的值。本文选择Sigmoid激活函数，即在神经网络中互相传递的值，均以式(9)进行传递。正向传播的最后一步为计算传递到输出层的值与期望输出值之间的误差[27]：

(10)

式中：tk为期望值，pk为实际输出值，k为样本数；对于本文所构建的DNN，tk为训练样本中瞬变场参数u的值，pk为训练样本中F(u)经神经网络各层神经元传递到输出层的值。

(11)

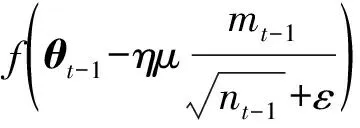
2.2 DNN模型参数的选择及优化

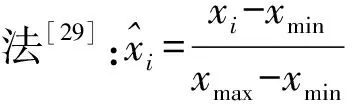
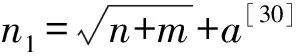
表1 人工神经网络隐含层不同神经元个数的误差情况Table 1 The convergence of different numbers of neurons in the hidden layer of ANN %

从表1及训练过程中可得出：

1) 训练过程具有一定的随机性，不同神经元个数具有不同的训练误差，神经元个数为13时，训练结果相对较好；

2) 当训练样本数为100时，增加其隐含层神经元个数，训练误差下降到0.002 5后较长时间没有下降，可能为训练过程中出现局部极小值所致；

3) 当训练样本数为200时，训练误差能够较快速跳出局部极小值，训练结果更加精确。

据此确定本文隐含层第一层神经元个数为13个。第二层是输入数据层神经元个数的1/3～2/3，第三层神经元个数也是第二层神经元个数的1/3～2/3； 将二、三层结构倒置过来作为第四、五层[17,25]。据此本文构建的DNN结构1～5层的隐含层神经元个数分别为：13、8、5、8、13。

本文使用上述5层DNN结构及神经元个数，训练样本数定为200，选择Nadam算法[27]对其进行 40 000次训练。在2.40 GHz的PC上完成训练，耗时1 232 s，训练结束后误差为1.197 8×10-5。误差下降曲线如图4所示，误差下降曲线总体呈单调下降，在局部极小值点附近，误差下降较慢，有一定的波动，但可有效跳出局部极小值。

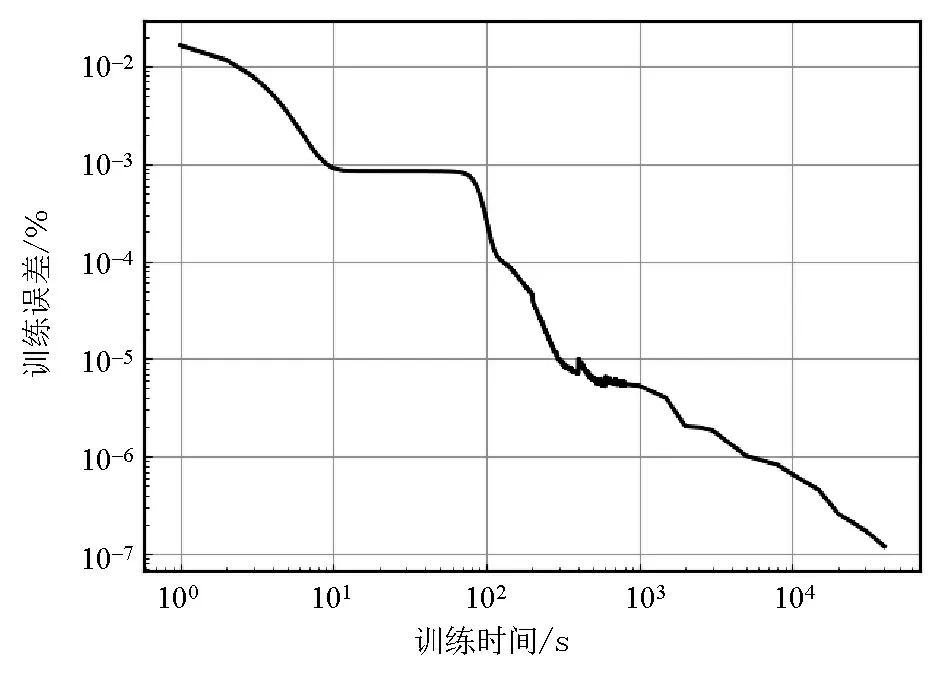
图4 深度神经网络Nadam训练算法误差下降Fig.4 The convergence reduction graph of the DNN Nadam training algorithm

2.3 DNN模型训练误差对比

瞬变场参数u的精度对视电阻率的影响极大，需要构建极为精确的DNN模型。实际应用中还未有完善系统化的理论来指导样本的选取，在没有公认确定使用何种处理方法可以得到较好效果时，要提高所构建的DNN模型的精度，一个非常重要的方法就是增大训练样本数量[28]。本文依据文献[19]选取训练样本数量及结合小批次的梯度下降算法，选取200 000组训练样本，发射电流为1 A，发射线框半径a=300 m，在训练过程中，将误差为4.675 6×10-6、5.531 1×10-7的2个DNN模型进行保存，用以对比分析不同训练误差DNN的实际使用效果。选取电阻率为100 Ω·m的均匀半空间地电模型进行试算验证，结果如图5所示：在探测深度较浅时视电阻率基本一致，探测深度较深时DNN需要更高的精确度；训练误差达5.531 1×10-7的DNN模型能够更精确计算较深部的视电阻率。

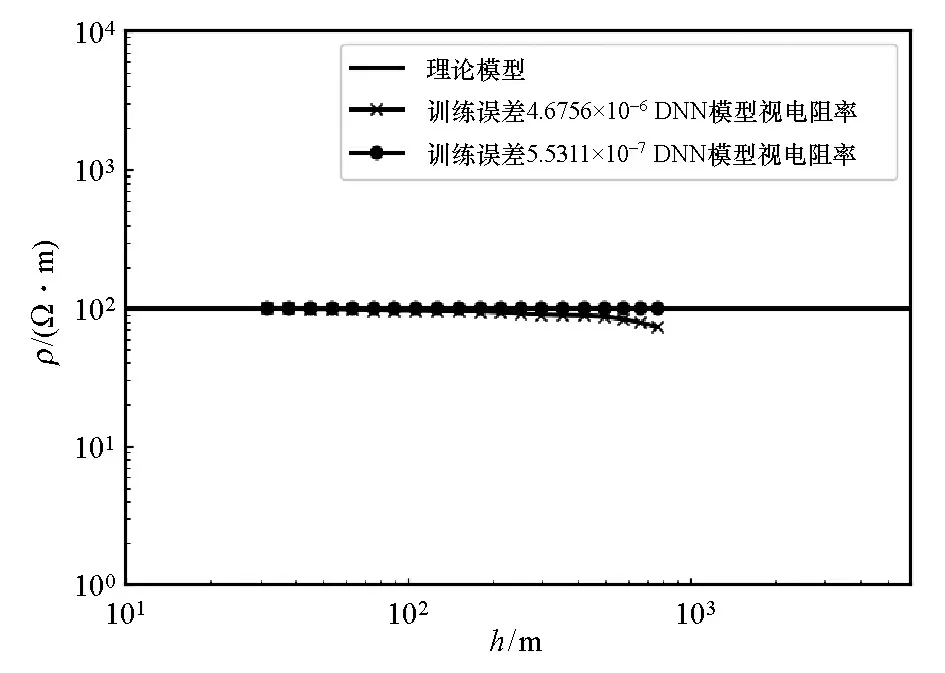
图5 不同训练误差DNN视电阻率对比Fig.5 Comparison of DNN apparent resistivity with different training convergence

3 仿真实验

仿真实验选取200 000组训练样本，发射电流为1 A，发射线框半径a为300 m，使用训练误差达5.531 1×10-7的DNN模型计算视电阻率。设计了几种地电模型：①均匀半空间地电模型，电阻率100 Ω·m；②H型地电模型，ρ1=500 Ω·m，h1=100 m，ρ2=10 Ω·m，h2=200 m，ρ3=500 Ω·m；③K型地电模型，ρ1=10 Ω·m，h1=100 m，ρ2=200 Ω·m，h2=100 m，ρ3=10 Ω·m；④四层KH型地电模型，ρ1=50 Ω·m，h1=50 m，ρ2=500 Ω·m，h2=100 m，ρ3=10 Ω·m，h3=200 m，ρ4=500 Ω·m。将仿真正演出不同地电模型的感应电动势转化为归一化感应电动势并代入训练好的DNN模型，由此得到所对应的瞬变场参数u，将其转换为视电阻率并计算出视深度后进行成像，得到视电阻率与视深度断面(图6)。

从图6可看出，基于深度学习所得视电阻率与本文所设计的地电模型相符。图6a由DNN所得视电阻率与理论模型视电阻率吻合很好。图6b显示DNN得到的视电阻率对低阻地层反映相对较好。图6c反映出由DNN所得视电阻率在高阻层与理论值相差较大，只能看出相对变化的趋势，说明其对高阻层反映不敏感，这也是瞬变电磁法的固有特点。图6d为四层KH型地电模型，由DNN所得视电阻率对其也具有良好反映，证实了该方法对复杂层状大地的适用性。

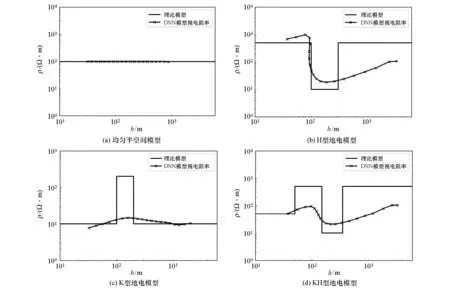
图6 4种地电模型视电阻率与视深度示意Fig.6 Schematic diagram of apparent resistivity and apparent depth of 4 geoelectric models

4 应用实例

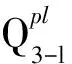
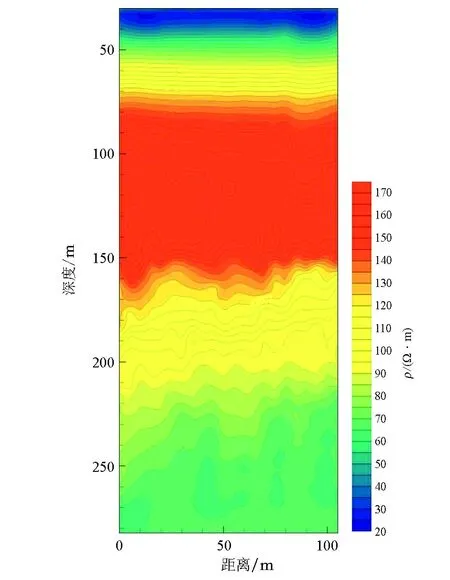
图7 和静水资源勘察视电阻率拟断面Fig.7 Schematic diagram of apparent aesistivity and depth of Hejing’s water resources survey

该测线分布在测区中部，呈近SN向展布，由北向南测量，剖面全长100 m，测点间隔5 m。从图7中可见，视电阻率总体呈现出中部高阻、上下低阻的特征，其中在50 m以浅可见深蓝色低阻条带，其视电阻率在50 Ω·m以下；向下在50～160 m范围处，出现高阻覆盖层，电阻率常见150 Ω·m，该高阻覆盖层延续性也很好；该地层下部存在延续性良好的低阻地层，推测该高阻地层可能为承压水的顶板；在250 m附近出现条带状低阻地层，平均视电阻率60 Ω·m，根据其低阻特征及其上覆盖高阻致密层，认为该处极大可能为承压水层。后期通过钻探进行验证，和推断结果相符。

5 结论及讨论

1)深度学习相较于传统人工神经网络，对抽象数据的拟合能力更强，本文将其应用于瞬变电磁视电阻率计算。使用Tensorflow2.0构建归一化感应电动势与瞬变场参数的5层DNN模型，并对各隐含层神经元个数进行确定。训练算法选择Nadam算法，该算法能够加速训练过程，能取得较好的训练效果。

2)本文以瞬变场参数u=1.613 6为界，建立了了2个DNN模型求解视电阻率，并讨论了延时范围与电阻率的关系，DNN计算视电阻率选取判别图可较好解决计算视电阻率存在双值的问题。在观测时间较长时，对DNN的精度要求更高，对训练的DNN精度需要达到何种程度，还需要进一步的研究。

3)本文训练好的DNN模型在实测资料处理中取得了良好的使用效果。DNN在瞬变电磁的实际应用还较少，可以针对不同装置训练出与之对应的DNN，将训练出的符合精度要求的DNN运用到实际工作中。虽然训练过程费时较多，但使用保存好的DNN模型不需要进行大量迭代计算，将数据代入DNN模型就可迅速计算视电阻率，能够极大提高视电阻率计算效率。

4)影响DNN训练的参数也较多，调整不同参数就可能对训练的DNN造成较大的影响。DNN对于不同参数的选择现在还没有统一的结论，对于不同情况，要训练出符合精度要求的DNN还需要大量实验。

致谢：感谢审稿专家提出的修改意见和编辑部的大力支持！