圆锥曲线中与焦点有关的等角问题
陕西师范大学附属中学(710061) 李朋涛
准备知识在全日制普通高级中学教科书(必修)《数学(第二册(上))》(2006年人民教育出版社)第138-139 页的阅读材料“圆锥曲线的光学性质及其应用”中给出了圆锥曲线的光学性质,现在叙述如下:
(1)从椭圆一个焦点发出的光,经过椭圆反射后,反射光线经过椭圆的另一个焦点.
(2)从双曲线一个焦点发出的光,经过双曲线反射后,反射光线的延长线经过双曲线的另一个焦点.
(3)从抛物线的焦点发出的光,经过抛物线反射,反射光线平行于抛物线的对称轴.
教科书中并没有给出证明,证明过程请参见文献[1-2].
准备知识2(角平分线定理)在∆ABC中∠A的内角平分线AD交BC于点D,则有∠A的外角平分线AE交BC于点E,则有
值得注意的是角平分线定理的逆定理也是成立的.使用面积法易证角平分线定理,这里不再赘述.

图1
下面我们来看一道引例.
题目1(2006年北京大学自主招生保送生测试题)已知F1、F2为椭圆的两个焦点,过椭圆外一点P作椭圆的两条切线,切点分别为A,B,求证:∠APF1=∠F2PB.
证明作出F1关于切线PA的对称点F′1,由椭圆的光学性质可知F′1、A、F2三点共线;同理作出F2关于切线PB的对称点F′2,由椭圆的光学性质可知、B、F1三点共线,如图2 所示.

图2
因F′1F2=F′1A+AF2=AF1+AF2=BF1+BF2=BF1+BF′2=F1F′2,又由对称性可知PF′1=PF1,PF2=PF′2,从而可知∆PF′1F2∽= ∆PF1F′2,所以∠F′1PF2= ∠F1PF′2,因此有∠F′1PF1= ∠F2PF′2,即2∠APF1=2∠BPF2,所以∠APF1=∠F2PB,证毕.
注通过∆PF′1F2∽= ∆PF1F′2我们还可以得到:∠PF1A=∠BF1P,∠PF2A=∠BF2P.
于是通过对题目1 的解答我们得到如下性质:
性质1(椭圆等角性质)已知F1、F2为椭圆的两个焦点,过椭圆外一点P作椭圆的两条切线,切点分别为A,B,则有下面结果:
①∠APF1=∠F2PB;
②∠PF1A=∠BF1P,∠PF2A=∠BF2P.
那么,我们自然会问这个结论对双曲线和抛物线是否也成立.笔者经过探究发现在双曲线和抛物线中也有类似的结果.现展示如下:
性质2(双曲线等角性质)已知F1、F2为双曲线的两个焦点,过双曲线外部一点P(把含双曲线焦点的区域称为该双曲线的内部)作双曲线的两条切线PA、PB,切点为A、B.
(i)若切点在双曲线的异支上,则有下面结果:
①∠APF1=∠F2PB;
②∠PF1A+∠BF1P=π,∠PF2A+∠BF2P=π.
(ii)若切点在双曲线的同支上,则有下面结果:
①∠APF1+∠F2PB=π;
②∠PF1A=∠BF1P,∠PF2A=∠BF2P.
证明(i)作出F1关于切线PB的对称点F′1,由双曲线的光学性质可知F′1、F2、B三点共线; 同理作出F2关于切线PA的对称点F′2,由双曲线的光学性质可知F′2、F1、A三点共线,如图3 所示.

图3
因F′1F2=BF′1−BF2=BF1−BF2=AF2−AF1=AF′2−AF1=F1F′2,又由对称性可知PF′1=PF1,PF2=PF′2,从而可知∆PF′1F2∽= ∆PF1F′2,所以∠F′1PF2= ∠F1PF′2,因此有∠F′1PF1= ∠F2PF′2,可知∠APF1= ∠BPF2,即2(∠F′1PF2+∠BPF2) =2(∠F1PF′2+∠APF1),所以∠APF1=∠F2PB.
又由∆PF′1F2∽= ∆PF1F′2可知∠PF1A+∠BF1P=∠PF1A+ ∠BF′1P= ∠PF1A+ ∠PF1F′2=π,同理可得∠PF2A+∠BF2P=π.
(ii)作出F1关于切线PA的对称点F′1,由双曲线的光学性质可知F′1、F2、A三点共线;同理作出F2关于切线PB的对称点F′2,由双曲线的光学性质可知F′2、F1、B三点共线,如图4 所示.
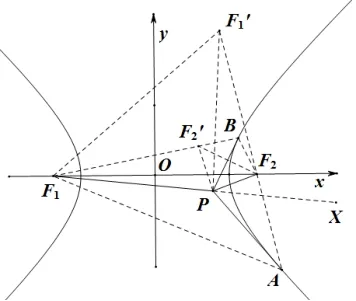
图4
因F′1F2=AF′1−AF2=AF1−AF2=BF1−BF2=BF1−BF′2=F1F′2,又由对称性可知PF′1=PF1,PF2=PF′2,从而可知∆PF′1F2∽= ∆PF1F′2,所以∠F′1PF2=∠F1PF′2,因此有∠F′1PF1= ∠F2PF′2,可知即∠XPA=∠BPF2(X为F1P延长线上一点),所以∠APF1+∠F2PB=∠APF1+∠XPA=π.
又 由∆PF′1F2∽= ∆PF1F′2,显然可知∠PF1A=∠BF1P,∠PF2A=∠BF2P,证毕.
性质3(抛物线的等角性质)已知F为抛物线的焦点,过抛物线外部一点P(把含抛物线焦点的区域称为该抛物线的内部)作抛物线的两条切线PA、PB,切点为A、B.则我们有下面结果:
①过P作直线PM平行于抛物线的对称轴且交AB于点M,则∠APF=∠MPB;
②∠PFA=∠BFP.
证明作焦点F关于切线PA、PB的对称点F′、F′′,如 图5 所示,由抛物线的光学性质可知AF′、BF′′均平行于抛物线的对称轴,所以直线F′F′′为抛物线的准线.

图5
由对称性可知PF′=PF=PF′′,所以可知∠AF′P=+∠PF′′F′= ∠BF′′P,故∠AFP=∠AF′P=∠BF′′P=∠BFP.
又因2π=∠AF′P+∠F′PF′′+∠PF′′B=2∠AFP+∠F′PF′′= 2(∠AFP+ ∠APF+ ∠BPF),所 以 可 知∠AFP+ ∠APF+ ∠BPF=π,而∠AFP+ ∠APF+∠PAF=π,从而有∠PAF= ∠BPF,由此可知∆APF∽∆PBF.
因AF′//BF′′//PM可 知∠APF= ∠PBF=∠PBF′′=∠MPB,证毕.
总结比较一下我们得到的椭圆,双曲线及抛物线中的规律,发现它们不尽相同,但是如果将这些角看作有向角时,则这些规律在椭圆,双曲线及抛物线中就得到了统一.即我们得到了圆锥曲线的一个统一结论:已知F1、F2为圆锥曲线(椭圆,双曲线,抛物线)的两个焦点,过圆锥曲线外一点P作圆锥曲线的两条切线,切点分别为A,B,则我们有下面结果:.(其中“”指的是有向角,如指的是直线AO绕点O逆时针旋转到与直线OB重合时所经过的角;对于抛物线的第二个焦点可以理解为在无穷远点).
以下我们关注有关圆锥曲线焦点三角形外角平分线的一个性质.首先来看如下的引例:
题目2(2019年全国高中数学联赛甘肃省预赛试题)已知椭圆1 的右焦点为F,过点G(4,0) 作斜率不为0 的直线交椭圆于M,N两点,设直线FM,FN的斜率分别为k1,k2,是判断k1+k2是否为定值,若是定值,求出该定值;若不是定值,请说明理由.
说明此题答案为k1+k2= 0,解答略.如图6 所示,笔者发现题中弦MN与x轴的交点G正好在椭圆的准线上,而k1+k2= 0 说明FG是∠MFN的外角平分线.那么此题的结论是否具有一般性呢? 若具有一般性那么能否推广到双曲线和抛物线中呢? 带着这些问题笔者分别对椭圆,双曲线及抛物线进行了一系列探索,得到了如下结论:
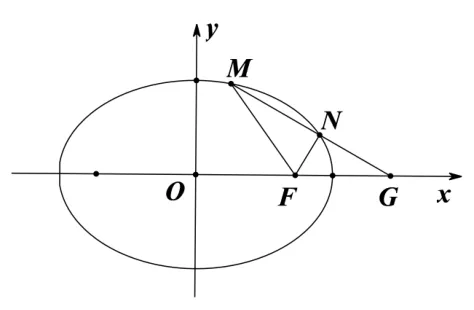
图6
性质4已知F1,F2为椭圆的两个焦点,弦PP′交准线l于点K,则F1K平分∠PF1P′的外角.
证明如图7 所示,过P、P′作准线的垂线,垂足分别为A、B.由圆锥曲线第二定义及平行线分线段成比例可知由角平分线定理逆定理可知F1K平分∠PF1P′的外角,证毕.

图7
推论1当P′与P重合时,此时弦PP′变为过P点的切线,则有结论F1K ⊥F1P.
性质5已知F1、F2为双曲线的两个焦点,弦PP′交准线l于点K.
(i)当P、P′在双曲线同支上时,如下图8 所示,则F2K平分∠PF2P′的外角.
(ii)当P、P′在双曲线异支上时,如下图9 所示,则F2K平分∠PF2P′.
证明(i) 如图8,过P、P′作准线的垂线,垂足分别为A、B.由圆锥曲线第二定义及平行线分线段成比例可知由角平分线定理逆定理可知F2K平分∠PF2P′的外角,证毕.
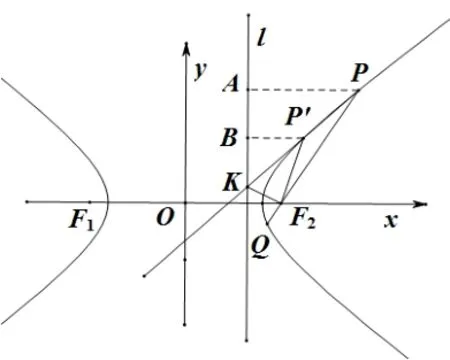
图8
(ii) 如图9 所示,过P、P′作准线的垂线,垂足分别为A、B.由圆锥曲线第二定义及平行线分线段成比例可知,由角平分线定理逆定理可知F2K平分∠PF2P′,证毕.

图9
推论2当P′与P重合时,此时弦PP′变为过P点的切线,则有结论F2K ⊥F2P.
性质6已知F为抛物线的焦点,弦PP′交准线于点K,则FK平分∠PFP′的外角.
证明作P、P′在准线上的射影A、B,如图10 所示,由抛物线定义及平行线分线段成比例可知由角平分线定理逆定理可知FK平分∠PFP′的外角,证毕.
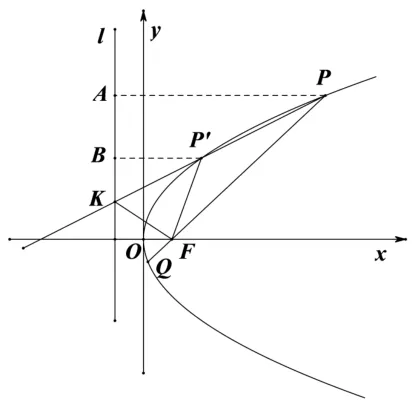
图10
推论3当P′与P重合时,此时弦PP′变为过P点的切线,则有结论FK ⊥FP.
总结由性质4-6,我们到了圆锥曲线的一组统一性质:已知F为圆锥曲线(椭圆,双曲线,抛物线)的一个焦点,直线l为焦点F对应的准线,弦PP′与准线l交于点K,则FK平分∠PFP′的外角.特别地,当P′与P重合时,此时弦PP′变为过P点的切线,则有FK ⊥FP(当P,P′在双曲线异支上时例外).
圆锥曲线的知识丰富多彩,引人入胜,只要我们在平时教学中多留意,多探索就能发现圆锥曲线更多的性质.

