全国林草资源调查机载大光斑激光雷达挂飞检校和验证

刘迎春,高显连,贺 岩,崔晨彦,高剑新,俞家勇,蔡龙涛,吴发云

(1.国家林业和草原局调查规划设计院,北京 100714；2.中国科学院上海光学精密机械研究所,上海 201800；3.安徽建筑大学,合肥 230601；4.东北林业大学,哈尔滨 150040)

森林是全球重要的陆地生态系统,可通过样地调查的方法评估其资源量和生物量[1-2]。随着激光雷达技术的发展,采用星载大光斑激光雷达估算大区域森林地上生物量将成为另一种选择。由于星载激光雷达数据少,近20年基本都围绕着美国的GLAS(Geoscience Laser Altimeter System)数据开展激光雷达林业应用研究[3-6],或者采用仿真大光斑激光雷达的方法进行前瞻性研究[7]。直到近年,GEDI(Global Ecosystem Dynamics Investigation)和高分7号发射,以及专门用于森林观测的陆地生态系统碳监测卫星(陆地碳卫星)预计于2022年发射,弥补激光雷达数据的不足。陆地碳卫星搭载了5个波长为1 064nm的激光器,能够在大光斑足印处获取高精度森林高度。

为发展和验证陆地碳卫星光斑尺度森林高度和生物量模型,国家林业和草原局调查规划设计院按照陆地碳卫星指标研制的全国林草资源调查机载大光斑激光雷达系统(National Forest and Grassland Inventory Airborne Large-footprint LiDAR,NFGI-LIDAR-L),可以在2 500m航高获取水平方向直径25m、垂直方向间隔0.15m的激光雷达波形数据。由于森林的空间异质性高,激光雷达定位精度直接影响了波形与树高调查数据的匹配精度,进而影响到大光斑激光雷达估算森林高度模型的精度。因此,在大光斑激光雷达应用到森林资源调查之前,需要实现高精度几何检校。

大光斑激光雷达几何检校方法包括地面探测器法、机载红外相机成像法、角棱镜反射法、平坦地形检校法、倾斜地形检校法、森林高度匹配法等[8-11]。目前来看,地面探测器法的精度高、适用范围广、使用较多,已用于GLAS、资源三号02星、高分7号检校。星载大光斑激光雷达检校水平精度约为10m、垂直精度约为1m[9,11],这对于直径20～30m、平均树高10m的森林调查样地来说误差偏高。因此,高精度的几何检校方法对陆地碳卫星数据能否用于林业至关重要。

1 机载大光斑激光雷达测树原理

机载大光斑激光雷达以一定高度飞行,激光器发射激光脉冲,并记录发射波形能量和时间；激光脉冲到达地面并返回,记录接收波形能量和时间。接收波形包括了植被、地面、背景等信息的混合波形。其中:背景信息通过滤波去除；植被和地面波形及其高程通过波形分解提取,并计算森林高度(图1)。按照探测器采样频率1GHz,即采样间隔1ns计算,以光速为X299 792 458m/s换算为测距分辨率,其值为0.149896m/ns≈299792458/(2×109)m/ns,这样可将波形时间换算为距离。

图1 机载大光斑激光雷达接收波形特征Fig.1 Characteristics of received waveform for airborne large-footprint LiDAR

2 激光雷达挂飞检校方法

2.1 激光雷达检校试验

大光斑激光雷达检校场地位于海南省儋州市西庆机场(北纬19.55°,东经109.43°)。机场周边以三叶橡胶(Heveabrasiliensis)人工林为主,零散分布有居住地、道路、农地等。机场周边地势平坦,机场内以草地、跑道和裸地为主。在机场内平坦空地上,选取以砂石为主的地面,并清理了地表较高的杂草和砖块,用于布设地面激光探测器(图2)。机载大光斑激光雷达数据采集时间为2020年12月2日16:00—17:30,云层高度为2 400m。用Cessna 208飞机搭载NFGI-LIDAR-L,以2 000m和1 500m两个相对航高、240km/h航速,采用交叉航线飞行,共获取6条航线数据。

图2 全国林草调查机载大光斑激光雷达检校场和地面激光探测器布设点位Fig.2 Calibration site of NFGI-LIDAR-L and distribution of ground Laser detectors

NFGI-LIDAR-L主要由大光斑激光雷达系统、位置和姿态系统、稳定平台系统、飞行管理系统、航空摄影系统、数据后处理系统组成。相较于上一套机载大光斑激光雷达系统[12],NFGI-LIDAR-L的激光器发射频率由40Hz改为40～200Hz可调,脉冲宽度由1.57ns改为3.037ns,扫描角由0°改为±15°,激光发散角由5mrad改为10mrad,波形采样间隔均为1ns(表1)。为保障高精度快速解算数据,在机场架设了一台采用实时动态载波相位差分定位技术(Real-Time Kinematic,RTK)的基站。

表1 全国林草资源调查机载大光斑激光雷达 地面激光探测器参数及航飞和检校场情况Tab.1 Parameters of NFGI-LIDAR-L,ground Laser detector,flight and calibration site

用RTK流动站从基站引点到检校场,按照5m×5m间隔,顺序布设了100个直径11cm的地面激光探测器(图2)。在航飞前后,用全站仪多次测定探测器的位置,精确到1mm。地面激光探测器专门用于NFGI-LIDAR-L的几何标定研究,探测激光的中心波长为1 064nm,频率高于200Hz,记录接收到激光的能量和时间。探测激光能量密度的范围为0.05～1.00 nJ/cm2,按照能量密度线性划分4 095个等级。探测器接收GPS时间,并与之时间同步；探测器之间时间同步误差为6μs。

航飞结束后,筛选探测器获得的完整大光斑激光雷达足印,共8个。其中:2 000m航高由18个、16个和15个探测器探测到的足印分别为3个、2个和1个,共6个；1 500m航高由12个探测器探测到的足印2个。

2.2 基于激光能量分布特征计算大光斑中心位置方法

由于地面激光探测器间隔5m,用探测器难以直接捕获到激光雷达的中心位置。本文基于激光能量自中心向边缘逐渐降低且能量梯度成比例分布的特征,计算地面光斑理论中心和能量密度。假定在相对航高2 000m时,同一时间(1ms内)激光雷达探测器aij(i和j分别为行号和列号)的数值最大,计算以aij为中心的8个方向的能量梯度G(nJ/(m2·m)),并以能量梯度和探测器间距计算大光斑激光雷达中心能量密度(Wmax)和坐标(Xd,Yd,Zd)。通过实验室测定得到的激光能量密度W(nJ/m2)与探测器数值a之间的关系方程为:W=2.45638a+124.8。

(1)

以探测器a44(i=4,j=4)测得的能量密度最大(W44；i=4,j=4)为例((1)式),x方向最小的能量梯度为G44-43=(W44-W43)/5,y方向最小的能量梯度为G44-34=(W44-W34)/5。假定激光雷达的能量密度梯度在一个方向上是等比例变化,则

(2)

(2)式中:dx和dy分别为探测器坐标x和y方向W44到Wmax的距离。首先,通过解方程得到各参数值,并通过坐标变换得到激光雷达中心坐标；然后,通过克里金插值法得到大光斑激光雷达水平方向的能量分布。

2.3 机载大光斑激光雷达几何检校方法

大光斑激光雷达通过发射波形和接收波形的时间差测定载荷平台到地面足印的距离(d),根据平台的位置和姿态、激光发射角等计算地面足印的位置((3)式)。

(3)

(3)式中:

1)[XsYsZs]′为激光雷达地面点在WGS84地固直角坐标系的坐标。

2)[XgYgZg]′为Inertial Explorer解算后定位系统(GNSS/IMU)在WGS84地固直角坐标系的坐标。

3)C为载荷平台坐标系向当地水平坐标系的转换矩阵,计算公式如(4)式所示。(4)式中:L和B分别为平台在WGS84地固直角坐标系的经度和纬度(rad)。

4)R为载荷平台坐标系向当地水平坐标系的转换矩阵((5)式),涉及到由右手坐标系转为左手坐标系和坐标旋转；当飞机从南往北飞时,飞机坐标系跟地固坐标系的投影坐标系相一致。h,p,r分别为航向角、俯仰角、翻滚角。

(4)

(5)

5)CI-G为IMU坐标系到载荷平台坐标系的旋转矩阵。

6)[xyz]′为激光雷达出光点与载荷平台原点在载荷平台坐标系中的位置偏移量(m)。

7)d为激光雷达测距(m),由激光雷达数据采集系统获得。

8)CL-I为激光雷达坐标系转换为IMU坐标系的转换矩阵。本文采用了二参数法((6)式)和三参数法两种转换矩阵。

二参数法指通过确定激光雷达出光轴在激光雷达坐标系YOZ面投影与Z轴正方向的夹角(α)和激光雷达出光轴与激光雷达坐标系YOZ面投影的夹角(β)对设备进行几何检校[11]。

(6)

(6)式中:α=θ+ρ。θ由激光雷达测定的码盘读数(Ag)换算得到,θ=(Ag-93594)×360/163840(°)；ρ为设备左右安装角,即激光出光轴在激光雷达坐标系YOZ面投影与码盘角差值(°)。

三参数法指通过确定激光雷达坐标系与惯导坐标系X,Y,Z三个方向的安置角(h0,p0,γ0)对设备进行几何检校((7)式)。

由(3)式得到的Xs,Ys,Zs,需要从WGS84地固直角坐标系通过国际地球参考框架(ITRF)的7参数换算到CGCS2000地固直角坐标系[13-14],再换算到CGCS2000大地坐标系,最后换算为CGCS2000高斯投影3度带[15](中央子午线108°E,记为X2000,Y2000,Z2000)。

(7)

由于NFGI-LIDAR-L为±15°扫摆式200Hz激光雷达,所以在做几何检校之前,需要先使探测器数据与机载数据匹配。本文通过波形特征、码盘角及试算后检校参数是否能够适用到其他大光斑激光雷达点位等方法确定地面激光探测器探测到的大光斑激光雷达。由8个检校点得到探测器记录脉冲时间比NFGI-LIDAR-L记录时间晚1004±2μs。

以遍历法确定检校参数ρ和β,使得由激光发射计算得到的大光斑中心位置(X2000,Y2000,Z2000)与由探测器计算的理论大光斑中心位置(Xd,Yd,Zd)的残差(Δp)最小((8)式)。每个大光斑对应一套检校参数。

(8)

以遍历法确定检校参数ρmin和βmin,以及h0min,p0min,γ0min,使获得的所有大光斑位置残差的均方根差RMSE(εmin)最小((9)式),则认为该参数是最优检校参数。

(9)

本试验,n=8；最优参数计算的大光斑中心位置记为X2000_min,Y2000_min,Z2000_min。

2.4 精度分析和验证

由单个检校点最优参数得到的大光斑中心位置(X2000_i,Y2000_i,Z2000_i)与最优参数计算的大光斑中心位置(X2000_min,Y2000_min,Z2000_min)差(Δpi),可以视为探测器单次检校的大光斑中心位置与大光斑理论中心位置的误差((10)式)。

因检校参数导致的误差,可以通过比较三参数法与二参数法计算大光斑位置的均方根误差(RMSE)来评估计算精度((11)式)。

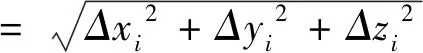
(10)

(11)

绝对高程精度的验证:2021年2月3日,利用RTK测量了12个高程精度验证点(Zki),测量精度为2cm,用于评价大光斑激光雷达绝对高程精度(ΔZ)。评价指标为均方根误差((12)式)、误差平均值和标准差。

(12)

相对高程精度的验证:采用与由机载小光斑激光雷达生产的高精度数字高程模型(DEM)进行比较的方法。2020年5月31日,通过搭载的Riegl VQ-1560i,获取了西庆机场及周边的小光斑激光雷达数据,点云密度10个点/m2。经过数据解算、航带匹配、去噪和精分类,以及提取地面点等处理,生成了1m分辨率DEM。通过地面控制点对DEM数据进行修正,得到高精度DEM数据。在试验区选择落在裸地、草地、森林、农田的大光斑激光雷达,用其地面回波的高程与DEM进行比较,评估其相对高程精度。

3 结果

3.1 大光斑中心位置和能量密度

与通过直接插值的结果相比(图3),根据激光能量分布特征解算的大光斑理论中心位置和能量密度分布结果(图4),大光斑能量密度分布更完整,跟发射波形(图5)的能量分布更一致,中心位置也更明确。

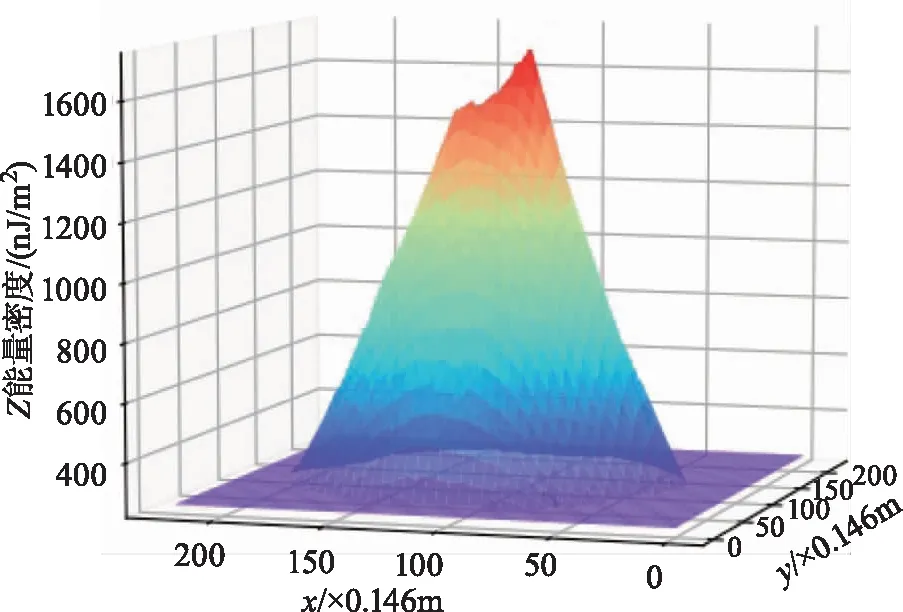
图3 探测器测定的大光斑能量密度用克里金插值法Fig.3 Energy density from ground Laser detector and interpolated by Kriging

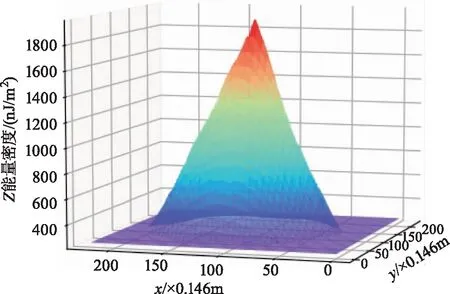
图4 根据激光能量空间分布解算后大光斑理论中心和能量密度分布Fig.4 The geocentric and energy density of large-footprint LiDAR calculated based on spatial pattern of laser from ground Laser detector

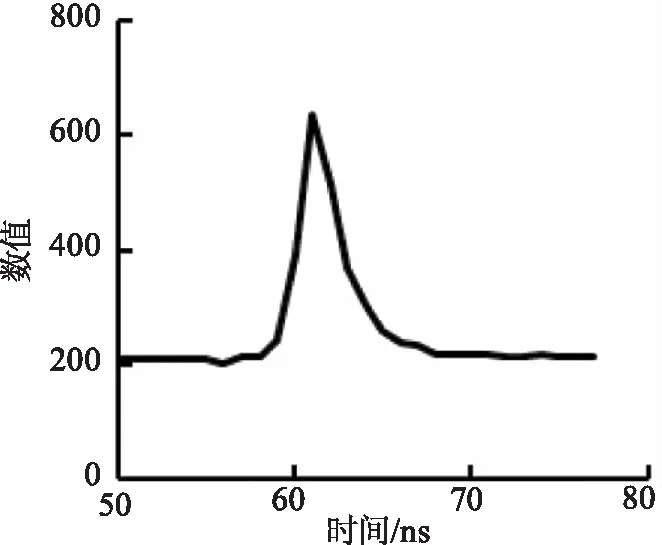
图5 NSGI-LIDAR-L记录的发射波形Fig.5 Transmitted waveform recorded by NSGI-LIDAR-L

在2 000m航高处,大光斑足印中心相较最大观测能量位置移动了1.27～3.47m,平均移动2.23m,移动方向没有明确规律；在1 500m航高处,2个大光斑足印中心相较最大观测能量位置分别移动1.36m和3.04m。在1 500m和2 000m航高,大光斑足印中心能量密度为2 197～2 221nJ/m2和1 554～2 060nJ/m2,平均为2 209nJ/m2和1 783nJ/m2。

3.2 激光雷达检校参数

激光雷达系统检校前(ρ=0,β=0),x,y,z方向的位置差分别为60.51,52.76,1.88m,总RMSE为80.30m。单个检校点使大光斑几何精度提高2个数量级,使总位置差降低到0.85～1.41m之间,平均为1.14m。其中,x,y,z方向的RMSE分别为0.82,0.78,0.05m。8个检校点得到的最优检校参数为ρ=2.2345°,β=-0.7732°；对应x,y,z方向的位置差分别为0.61,0.54,0.05m,总RMSE为0.82m(表2)。8个检校点得到的平均检校参数已经接近最优参数,说明通过8个检校点，能够获得比较精确的大光斑激光雷达中心位置。

表2 激光雷达系统二参数检校法的参数和检校前后位置差Tab.2 Constants of Two-parameter Calibration,and x,y,z and total RMSE pre-and post-calibration

从三参数检校结果看(表3),最优检校参数为h0=0.02,p0=0.7734,r0=2.231；x,y,z方向的RMSE分别为0.62,0.54,0.05m,总RMSE为0.82m。跟二参数检校精度基本一致。单检校点的位置差范围,x,y,z方向分别为0.64～1.12m,0.56～0.93m,0.05～0.06m,RMSE分别为0.82,0.78,0.05m。

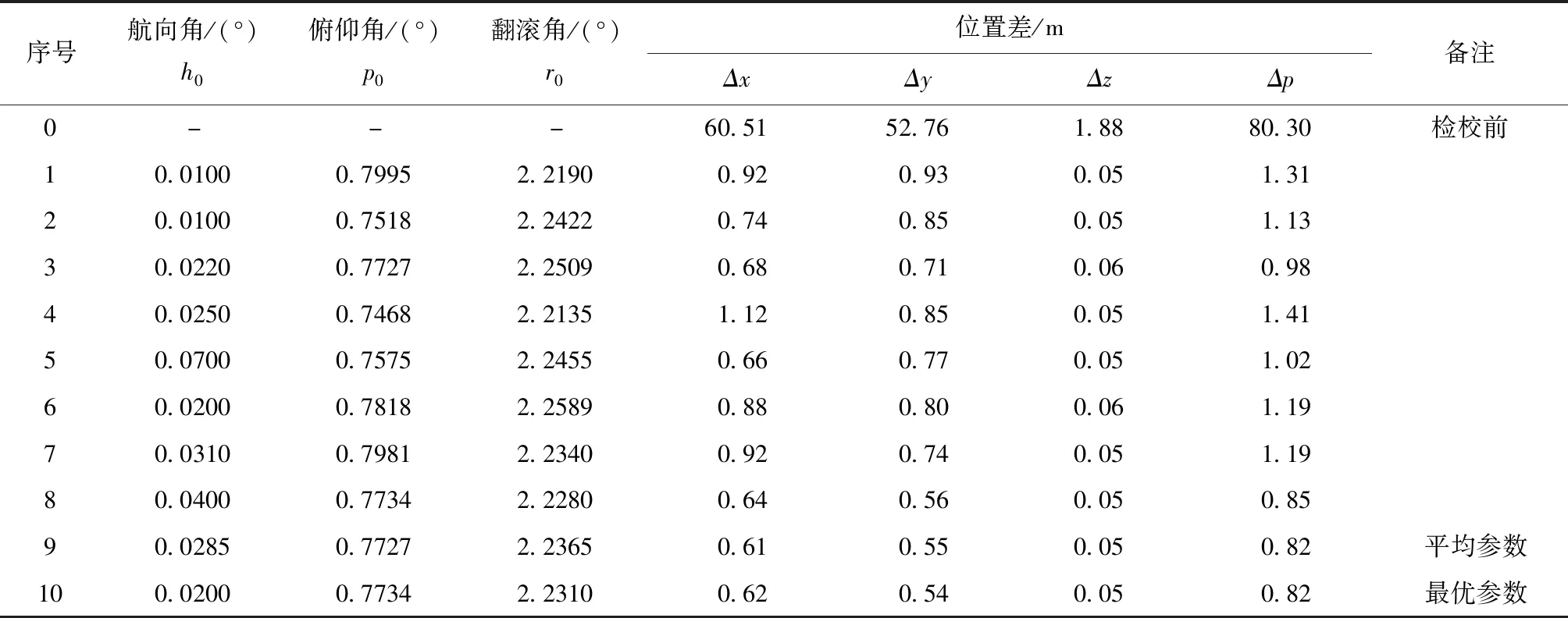
表3 激光雷达系统三参数检校和检校前后位置差Tab.3 Constants of Three-parameter Calibration,and x,y,z and total RMSE pre- and post-calibration

从三参数法与二参数法最优参数计算的大光斑中心位置差(表4)来看,x,y,z方向的平均位置差分别为0.083,0.094,0.002m,总平均位置差为0.125m。从影响因素来看,两种方法受到航高和码盘角影响。航高越高,误差越大；1 500m和2 000m航高的平均位置差0.101m和0.134m,并且主要集中在水平误差上。同一航高时,码盘角越大位置差越大。比如2 000m航高,码盘角为-0.74°,-1.67°,-2.38°,-3.48°时,位置差分别为0.129,0.132,0.134,0.137m。

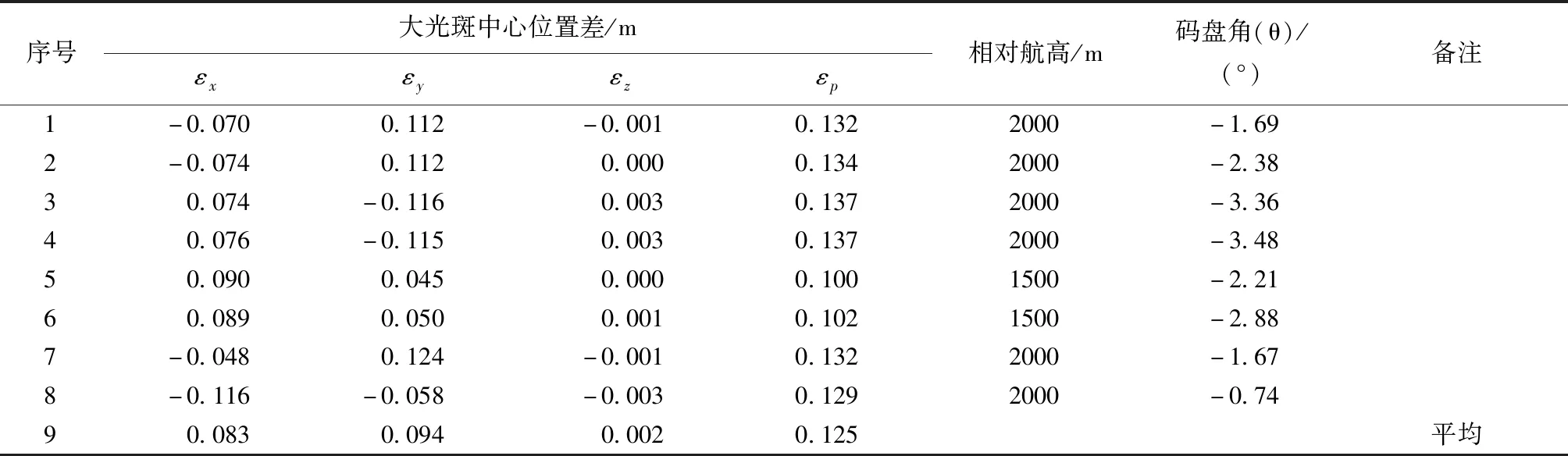
表4 三参数与二参数法最优参数计算的大光斑中心位置差 相对航高和码盘角Tab.4 RMSE between Three-parameter Calibration and Two-parameter Calibration,relative flight heights and angles of code wheel

3.3 激光雷达高程检校

以RTK检校点评估大光斑激光雷达绝对高程精度,高程差的变异范围为0.01～0.18m,均方根误差为0.12m,平均误差为0.10m,标准差为0.06m,检校点12个。大光斑激光雷达与检校点的高程差未出现随距离或激光扫描角度的增大而增大的现象。因此,NFGI-LIDAR-L检校后绝对高程精度在0.15m以内。

与小光斑激光雷达生成的高精度DEM相比,大光斑激光雷达得到的裸地和跑道、草地、农田、森林等地面高程均方根误差分别为0.13,0.15,0.38,0.58m,样本量分别为8,10,3,8。

4 讨论

4.1 激光雷达检校试验

2017年采用地形法得到的机载大光斑激光雷达几何检校的精度约为5m。卫星的地面激光探测器间距为10～25m,水平方向检校精度在10m左右[9,11],说明探测器间隔对水平检校精度影响较大。本文基于激光能量梯度计算大光斑中心位置的方法,使检校精度突破了0.5倍探测器间距限制,达到0.82m。

由于本次检校飞行的扫描角比较小(码盘角在-0.74°～-3.48°),采用三参数和二参数检校法的差异在0.1m级别,说明当扫描角小时(±1.5°),两种方法都能够得到比较精确的位置。随着扫描角的增加,三参数法可能会比二参数法检校精度高。相对航高也影响检校参数的精度,未来需要进一步通过试验验证。

4.2 激光雷达检校试验改进

由于地面探测器灵敏度高,可以支持更大角度机载大光斑激光雷达几何检校。未来可以通过增加探测器数量、提高探测器间距、变换不同航高(1 000m～3 000m)、增大扫摆角度(±5°,±10°)等试验,进一步获得更准确的大光斑激光雷达能量分布和中心位置,以提高大角度激光雷达的检校精度。

4.3 星载激光雷达检校展望

本文验证了采用地面探测器检校机载大光斑激光雷达的可行性。随着激光器数量增加,地面探测器检校法的工作量将大幅增加。如何对陆地生态碳卫星搭载的5个激光雷达进行几何检校,需要继续探讨。比如,探讨改变卫星姿态角,将卫星平台旋转90°,使5个激光器由垂轨分布改为沿轨分布,5个激光器发射的大光斑依次通过同一个地面探测器场,获得5个激光雷达相对位置；再将卫星平台转-90°,使激光器正常沿轨运行,之后多次观测其中1个激光器的光斑位置,从而实现5个激光器的精确检校。

5 结论

针对大光斑激光雷达检校精度不能满足林业应用的问题,本研究通过新研制的NFGI-LIDAR-L和地面激光探测器,用编写的大光斑激光雷达检校算法和基于激光空间分布特征计算大光斑激光雷达中心位置算法,实现了NFGI-LIDAR-L的几何检校。大光斑激光雷达几何精度从检校前的80.3m提高到0.82m,绝对高程精度达到0.12m。因此,通过地面激光探测器法对大光斑激光雷达进行几何检校的方法能够基本达到林业应用要求。

致谢:

野外工作期间,西庆机场提供试验场地,上海大恒精密机械有限公司吴致昊工程师和曹健东工程师获取飞行数据,山东科技大学研究生徐飞、刘冠杰、林景峰、宋成航参加检校场布设。他们为本研究提供了大力支持和诸多帮助,在此一并表示感谢。