超临界水在套管换热器中的流动传热试验研究
刘浪,李增光,杨建,何文强,王青青
1 中国舰船研究设计中心 上海分部,上海 201108
2 西安交通大学 能源与动力工程学院,陕西 西安 710049
0 引 言
超临界流体由于其特殊的性质,其传热过程非常复杂。在临界压力下,在拟临界温度附近很小的温度范围内,流体的密度、动力黏度会随着温度的增大显著减小,传热系数会出现一个峰值,随后迅速下降,呈抛物线分布。物性的剧烈变化对超临界流体传热流动特征有着重要影响。
而双超临界流体传热的套管换热器中耦合了变热流密度的边界条件,其传热流动过程更为复杂,伴随出现的一些特殊传热现象会严重影响换热器的合理设计。由于对双超临界流体传热机理的认识不足以及计算模型不合理,给套管换热器设计带来了困难。目前,有关套管换热器设计仍是采用常规通道下单超临界流体传热研究得到的一些计算方法进行,产生了较大的设计偏差,因此有必要对双超临界流体的流动换热特性进行深入研究。
超临界流体的针对性研究较多,且已有广泛的工程应用。Hall等[1]分析了超临界流体在管内的流动阻力和速度分布,讨论了热物性对超临界流体传热的影响。Jackson等[2-3]研究了超临界流体在圆管内的流动传热,分析了传热机理与湍流流动,并提出经验公式对浮力的影响进行了修正。Yoshida等[4]研究了超临界水和超临界二氧化碳的流动与传热特性,结果显示在低热流密度条件下,临界点附近流体的物性参数在很小的温度范围内发生了剧烈变化,远离临界点后(大于25~26 MPa),在拟临界点处物性的变化趋于平缓;流体物性剧烈变化是换热系数出现峰值的主要原因。Pioro等[5]研究了超临界水和二氧化碳在管内的流动换热,指出超临界流体在管内流动换热时,传热强化、传热恶化、正常传热并不是单一出现,而是各种现象可能同时存在。Cheng等[6]研究了超临界水在垂直上升管和垂直下降管内的流动与换热,并整理得到试验传热关系式,与前人提出的传热关系式对比,引入修正因子,得到传热关系式和阻力关系式,试验结果的预测误差在±10%以内。
Wang等[7]探究了超临界水在内螺纹管中的阻力特性和传热机理,总结出了拟临界区的传热恶化现象及其机理。Zhu等[8]研究了超临界水在垂直管内上升流的传热流动现象,试验中,水的温度上升至拟临界温度时,管道内会发生传热恶化。在低热流密度工况下,传热效果随着压力的增加不断削弱;在高热流密度工况下,传热恶化现象随着压力的增加有所改善。Wu等[9]研究了换热系数在倾斜管周向的分布规律和压力变化的影响,结果显示周向换热系数分布不均匀,而倾斜管内重力作用与物性变化叠加是主要原因。Wang等[10]研究了超临界水在垂直上升光管和内螺纹管内的流动与传热特性,并进一步分析了垂直上升管内温度的分布趋势,根据试验结果,得到了不同范围的传热关系式。
Zhao等[11]对超临界二氧化碳在垂直套管换热器中的耦合传热进行了数值研究,结果表明,混合对流是超临界二氧化碳耦合传热的主要传热机理,高黏度可以防止流场发生畸变进而降低传热恶化。Ma等[12]对超临界二氧化碳和超临界水在套管换热器中的流动进行了试验研究,发现超临界水侧的质量流量对传热的影响较为显著,而超临界二氧化碳侧的压力和水侧质量流量对浮升力影响不大,结果表明热边界层对超临界流体与其他流体之间的传热有着重要影响。
综上可以看出,超临界流体的流动和传热与一般流体的流动传热具有明显区别。本文试验研究将以超临界水冷堆为背景,模拟双超临界水在变热流密度边界条件下的传热过程,并开展相应的热工水力特性研究,获得相应的传热特征,深入理解双超临界水耦合传热的机理和流动传热规律,为今后的设计工作积累丰富的数据,从而为制定我国的新型反应堆、核动力系统设计和安全评定导则提供基础。
1 试验系统和试验方法
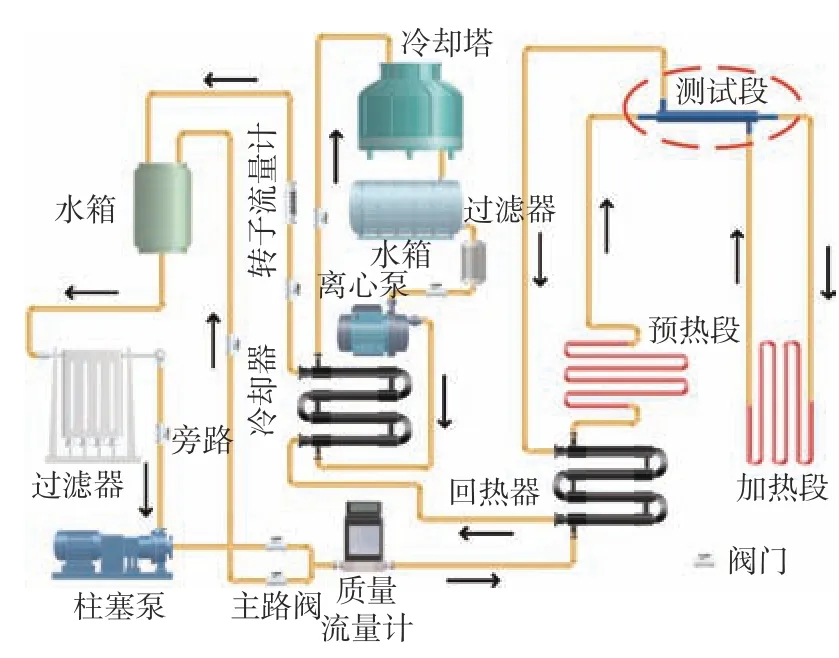
图 1 试验系统Fig.1 Testing system
试验基于高温高压气液两相流试验台,并广泛参考国内外资料以及实验室前期积累的超临界流体传热试验经验,试验系统的回路具体如下:储存在水箱中的等离子水经过滤网由高压柱塞泵(最高可实现40 MPa压力)升压后分为两路进入试验系统,一路作为主路外的旁路系统,用来调节管内流量和运行压力,另外一路经流量调节阀和孔板后进入换热段,去离子水在换热段吸收高温水的热量,随后进入预热段加热后,作为低温流体进入试验段内管,低温流体流经试验段后进入加热段并被低电压大电流电源加热,然后作为高温流体进入试验段外管与内管低温流体实现传热。换热结束后,试验段的高温流体流经换热段,经冷凝器冷却后返回水箱。凝汽器内的冷却水由凝汽泵泵送,出凝汽器后进入冷却塔冷却。试验段两侧的质量流量始终相等。试验中,调整预热段的功率进而稳定低温流体的入口温度。通过调节加热段功率,试验段高温流体可以与低温流体实现不同的传热状态。试验中所有的加热方法都是直接电加热,试验系统回路如图1所示。整个双超临界水耦合传热试验研究主要包括前期的套管试验段加工,热电偶测点布置、密封、连接,仪器仪表的连接、检测与校准,测试工况试运行,同时进行温度、压力、流量的测量与采集。试验段为水平套管换热器,如图2所示,试验段材料为316L不锈钢,套管换热器内管内径为15 mm,内管外径为20 mm,外管内径为35 mm,整个试验段换热长度为1 500 mm,距离换热器两端端口30 mm处为换热器的外管高温水进出口支管,在管长方向沿内管上、下外壁均匀布置20只K型热电偶丝,直径为0.3 mm,20只K型热电偶丝穿过套管换热器外管,接入数据采集器。套管内、外管的进、出口温度测量选用K型铠装热电偶,直径为3 mm。温度较低的超临界水通过内管入口进入,由内管出口流出,经过加热段加热为温度较高的超临界水后再由外管的入口进入,然后在换热器中完成换热后由外管出口流出。整个套管换热器外部包裹保温棉,以减少换热过程中向环境散热,套管换热器进、出口均装有罗斯蒙特3 051压力传感器,用于测量压力。
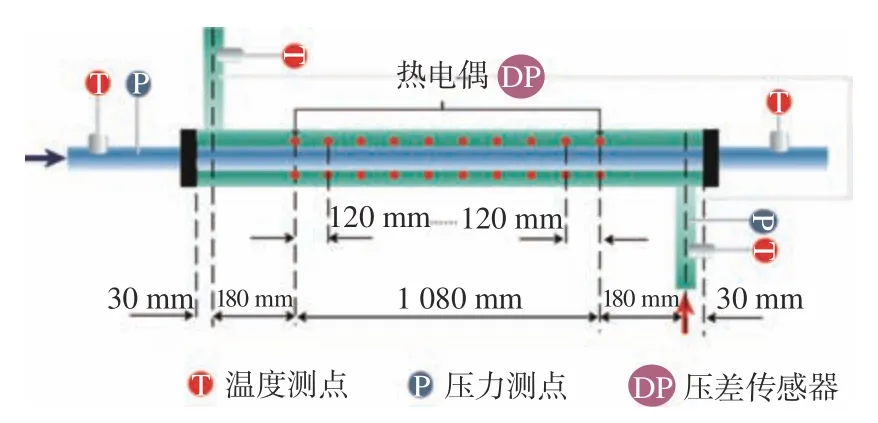
图 2 试验段结构及热电偶测点分布图Fig.2 Test section and the distribution of thermocouple measuring points
图3和图4所示分别为试验段测点分布及热电偶测点布置。试验段内布置有20个壁温测点(两两一组沿程布置),均匀分布于内管外壁沿管程上、下对称处,采集内管外壁沿管程上、下对称的20处温度,进行加权平均后求得内管外壁温度Tw。

图 3 试验段测点分布Fig.3 Distribution of measuring points in test section

图 4 试验段热电偶测点布置Fig.4 Thermocouple measuring points in test section
试验过程中,测得系统质量流量、套管内外管的进出口压力及压差、套管内外管的入口温度和出口温度、内管外壁温度、加热负荷等参数后,进行传热和流动阻力数据处理。
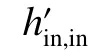
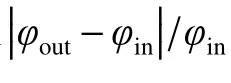
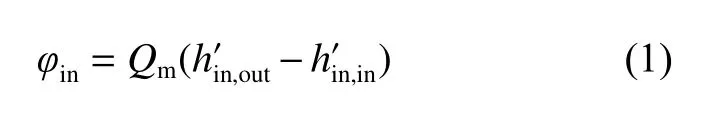

基于内管外侧换热面积计算得到的套管换热系数表示为

式中:Ao为内管外侧换热面积; Δt为内管流体与内管外侧表面的温差。参数计算式为:
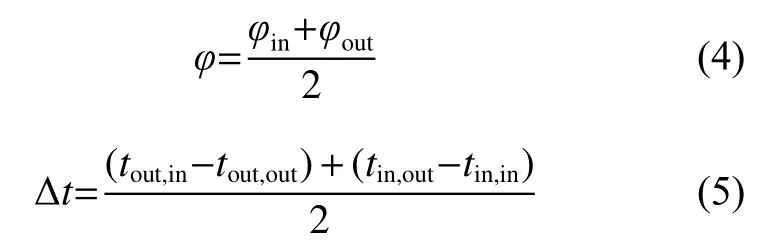
通过内管外壁温度Tw和主流温度Tb,可以计算外 管换热系 数hout。
试验过程中,
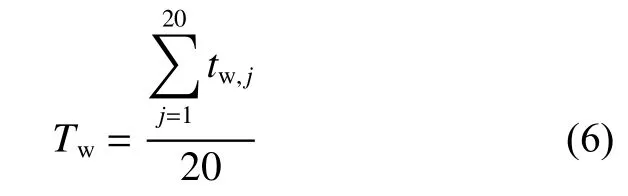
式中,tw,j为通过20个布置在内管外壁上的热电偶测得的每一个点的温度。取这20个热电偶温度的平均值,即可得到内管外壁温度Tw。
主流温度Tb通过布置在外管进、出口处的K型铠装热电偶测得的tout,in和tout,out计算得到。
Tb由式(7)计算得到:
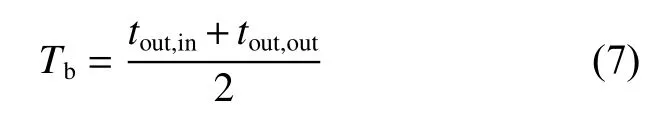
外管换热系数hout的计算式为

套管外管的努塞尔数Nu的计算式为

式中: λo为套管外管水对应的导热系数;D=do-di,为环形管的水力直径。
无量纲参数雷诺数Re的计算式为

式中: ηo为 套管外管水的动力黏性系数; ρo为 套管外管水的密度;uo为套管外管水的速度。
试验段的压降通过外管进出口的压力传感器测得的压力计算得到。阻力系数计算式为
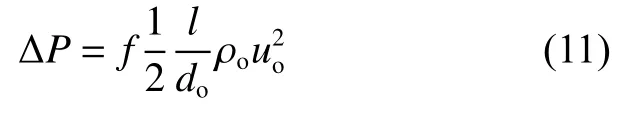
Filonenko公式拟合的超临界流动阻力关联式为
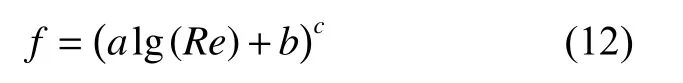
式中,a,b,c为待定系数,通过试验测量值计算得到。
根据文献[13]提出的方法,试验测量和计算参数的不确定度分析结果如表1所示。参数 不确定度/%
主流温度Tb±0.06内管外壁温度Tw±0.16
压力P±0.34质量流量Qm±0.74套管换热系数h±2.90外管换热系数hout±2.60
雷诺数Re±1.00努塞尔数Nu±2.68
2 试验结果分析
在套管换热器中进行超临界水的耦合对流换热试验,并设置主要参数,其中压力P=23,25,28 MPa,质量流量Qm= 541,573,604 kg/h,内管入口温度tin,in=290,320,350 ℃,外管入口温度tout,in=330~480 ℃。试验过程中,内、外管的质量流量始终保持一致,试验主要研究内管入口温度、压力和质量流量对流动传热的影响,进一步处理试验数据,分析换热机理,提出无量纲参数,整理得出传热关系式。
2.1 入口温度的影响
图5和图6所示为Qm= 573 kg/h,P=25 MPa的试验条件下,内管入口温度变化对换热系数的影响。由图5可见,换热器的总换热系数随着主流温度Tb的增加是先增加后降低,在拟临界区达到峰值。当主流温度Tb低于拟临界温度时,总换热系数随tin,in的增加而增加;当Tb高于拟临界温度时,总换热系数受tin,in的影响较小。这一现象可能是由浮升力效应所导致。
超临界流体在由拟临界区域热物理性质的急剧变化引起的截面上的径向密度梯度导致了浮力效应[14]。而随着超临界流体流量的减小或热负荷的增加,浮升力效应逐渐增强,强制对流换热逐渐转变为混合对流换热。
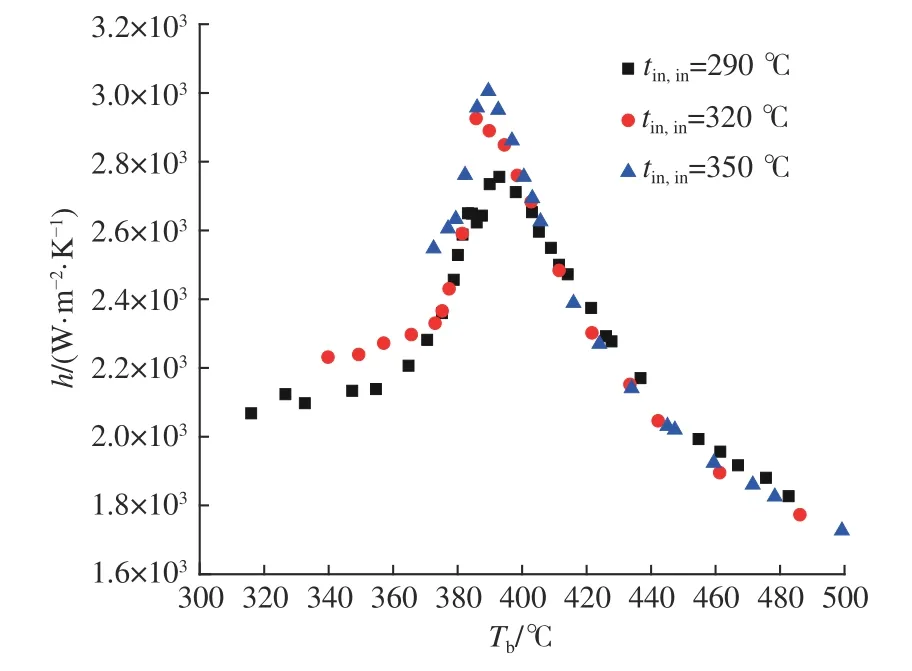
图 5 内管入口温度对套管换热系数的影响Fig.5 Influence of inlet temperature on heat transfer coefficient of the double-pipe heat exchanger
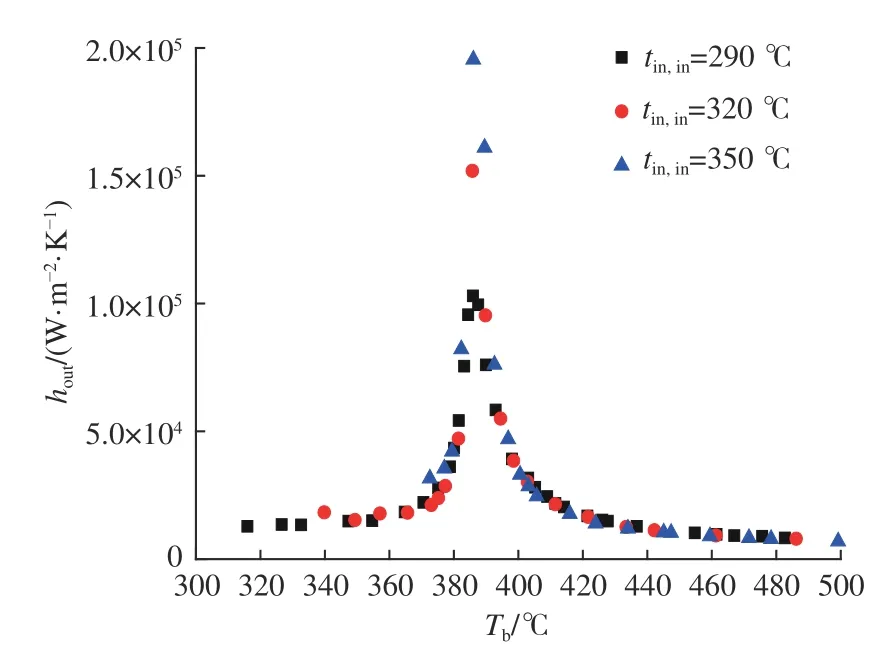
图 6 内管入口温度对外管换热系数的影响Fig.6 Influence of inlet temperature on heat transfer coefficient of the outer pipe
浮升力效应随tin,in的增加而减小。当tin,in=290和320 ℃时,浮升力效应在拟临界区显著。当tin,in=350 ℃时,浮升力对外管换热系数的影响并不显著。浮升力效应对传热的影响是不利的,因此,当Tb低于拟临界温度时,外管换热系数随tin,in的 增大而增大。当Tb高于拟临界温度时,浮升力效应不显著,因此外管换热系数几乎与tin,in无关。
如图6所示,tin,in对外管换热系数的影响与对套管换热系数的影响相似。
图7所示为在Qm= 573 kg/h,P=25 MPa的试验条件下,内管入口温度变化对外管进出口压差ΔP的 影响。由图可见,当tin,in由290 ℃增加至320 ℃最后增加至350 ℃时,外管的进、出口压差变化一致,即内管入口温度的改变对外管进出口阻力系数 基 本无 影 响。当tin,in=290 ℃时,随着Tb升 高,外管的进出口压差逐渐增加,管内阻力系数逐渐增加,明显发现,当主流温度Tb处于拟临界点区域时,外管进出口压差迅速增大,这是因为当质量流量不变时,在拟临界区流体的热物性发生剧烈变化,流体的密度急剧下降使得外管内流体速度迅速增加,进而使得压差增大,阻力系数增加。

图 7 内管入口温度对外管压差的影响Fig.7 Influence of inlet temperature of inner pipe on differential pressure of outer pipe
2.2 质量流量的影响
图8和图9所示为P=25 MPa,tin,in=320 ℃工况下,质量流量变化对2种换热系数的影响。由图8可见,不同质量流量下的套管换热系数随着Tb的升高是先升高再降低,在拟临界温度附近达到峰值;总体而言,增大质量流量可以提高套管换热器的总换热系数。由图9可见,外管换热系数几乎不受质量流量的影响,仅在拟临界温度区域附近随着质量流量的增加而略有变化。其原因可能是因为在试验中内、外管内的质量流量相同,一侧会抵消另一侧对外管换热系数的影响。
图10所示为P=25 MPa,tin,in=320 ℃工况下,不同质量流量下外管进出口压差 ΔP随Tb的变化趋势:当Tb低于拟临界温度时,质量流量的改变对外管进出口压差影响较小;当Tb高于拟临界温度时,外管进出口压差随着质量流量的增加而增加。这是由于随着质量流量增加,外管内流体速度增加,压差也会随着速度的增加而增加;而在拟临界温度点附近,水的密度发生剧烈变化,密度下降,管内速度迅速增大,外管进出口压差迅速增加。

图 8 质量流量对套管换热系数的影响Fig.8 Influence of mass flow on heat transfer coefficient of the double-pipe heat exchanger coefficient

图 9 质量流量对外管换热系数的影响Fig.9 Influence of mass flow on heat transfer coefficient of the outer pipe
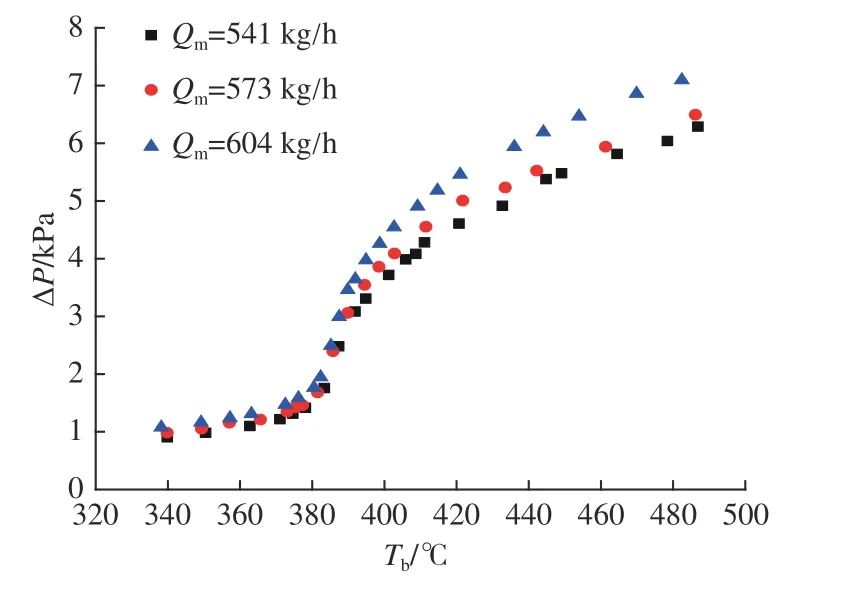
图 10 质量流量对外管进出口压差的影响Fig.10 Influence of mass flow on differential pressure of outer pipe
2.3 压力的影响
图11给 出 了Qm=573 kg/h,tin,in=320 ℃条 件下,套管换热系数在不同压力下随主流温度Tb的变化趋势。由图可见,在不同压力下,随着Tb的增加,套管换热系数增加,直至Tb升高至拟临界温度Tpc,套管换热系数达到峰值,然后随着Tb的增加而降低。在拟临界温度区域,套管换热系数峰值随管内压力的增大而减小,对应于套管换热系数峰值的温度随运行压力的增大而向高温侧移动。图12给 出 了Qm=573 kg/h,tin,in=320 ℃条 件下,外管换热系数在不同压力下随主流温度Tb的变化趋势。由图11和图12可见,外管换热系数与套管换热系数随Tb的变化趋势基本一致。此外,图11和图13(图中Cp为比热容)给出的超临界水在不同压力下随Tb的变化趋势相似,可以推断出拟临界温度区域的传热强化是由流体的热物性随温度剧烈变化所引起;远离临界压力点时,热物性随温度的变化趋缓,传热强化程度降低。
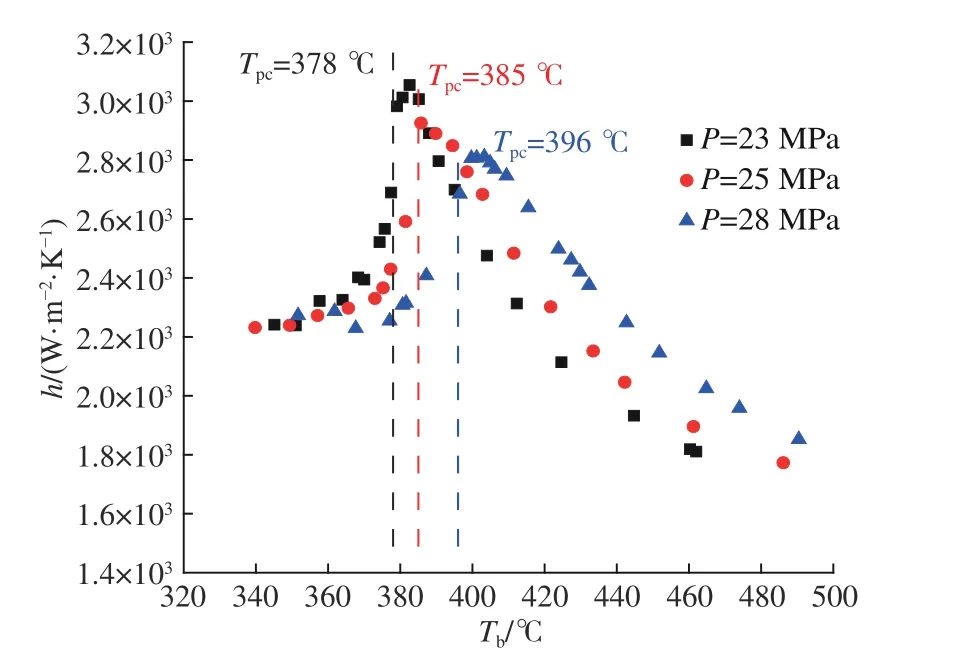
图 11 压力对套管换热系数的影响Fig.11 Influence of pressure on heat transfer coefficient the double-pipe heat exchanger
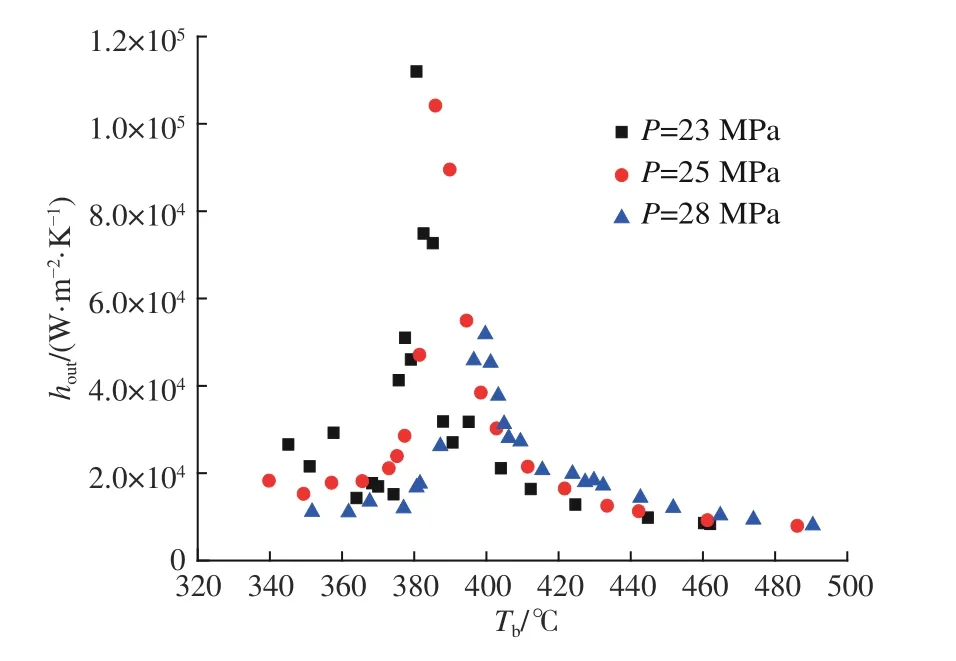
图 12 压力对外管换热系数的影响Fig.12 Influence of pressure on heat transfer coefficient of the outer pipe
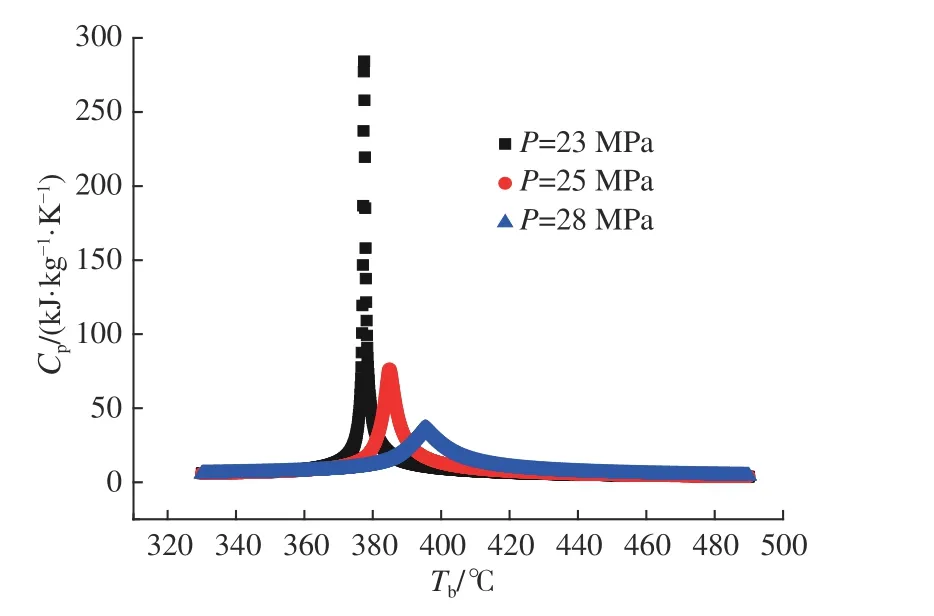
图 13 不同压力下的拟临界点Fig.13 Quasi-periodic critical point under different pressures
试验中发现,套管换热系数达到峰值的主流温度高于对应压力下的拟临界温度。这是因为传热通道的横截面存在温度梯度,外管靠近内壁面的温度总是低于外管环管横截面中心处,内管外壁面附近的温度先降低到拟临界温度,然后再降低到截面平均温度,拟临界区域很小范围温度梯度会引起物性的变化,使得套管换热系数峰值对应的温度略高于拟临界温度。当换热系数相同,流体压力较低时,流体温差变化较小。因此,随着运行压力的降低,截面温度梯度减小,套管总换热系数峰值对应的温度与拟临界温度的差值随运行压力的降低而减小。
同时可以发现,套管换热系数峰值对应的温度与拟临界温度之间的温差随着运行压力的降低而减小,产生这种现象的原因可能是超临界水的比热容在拟临界温度时达到峰值,峰值随运行压力的降低而减小了。
图14所 示 为Qm=573 kg/h,tin,in=320 ℃条 件下,运行压力对外管进出口压差的影响。随着Tb不断升高,外管进出口压差逐渐增大,尤其当Tb超过拟临界温度时,外管进出口压差随着管内压力的降低而迅速增加,外管内阻力迅速增加。造成该现象的主要原因是,当温度处于拟临界点附近时,流体密度降低,使得管内流体速度迅速增加,导致压差迅速增加。
2.3 农村留守儿童社会适应得分与其心理韧性得分的相关性 农村留守儿童社会适应各维度得分与其心理韧性各因子得分大都存在显著负相关。见表3。
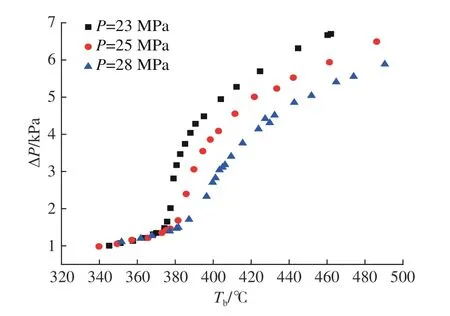
图 14 压力对外管进出口压差的影响Fig.14 Influence of pressure on differential pressure of outer pipe
不同压力下,外管压差随Tb的变化趋势基本一致,由于管内运行压力越接近临界压力,流体的物性变化越大,因此当运行压力P=23 MPa时,外管进出口压差迅速增加,对应的温度略低于25和28 MPa所对应的温度,前者的进出口压差增加幅度也较大。当Tb低于拟临界温度时,运行压力的差异对外管进出口压差基本无影响;当Tb处于拟临界温度区域,外管进出口压差变化幅度较大;当Tb超过拟临界温度后,压差随着运行压力的增加而逐渐下降,P=23 MPa时,随着Tb增加,外管进出口压差越大,最大压差为6.7 kPa;P=25 MPa时,最大压差为6.4 kPa;P=28 MPa时,最大压差下降至5.9 kPa。
2.4 传热和阻力关系式整理
2.4.1 传热关系式整理
诸多学者已提出超临界流体传热关系式,但均是建立在超临界流体变物性的单相流动传热工况下,采用雷诺数、努赛尔数、普朗特数加之物性修正项,如比热容比值修正因子Cpb/Cpw、密度比值修正因子 ρb/ρw、导热系数比值修正因子 λb/λw,不同工况下的传热关系式均有其适用范围,不能适应所有试验条件。为此,对比Dittus-Boelter公式以及Mokry等[15],Bishop等[16],Bringer等[17],Watts等[18],Jackson等[19],Hu等[20]通过试验结果整理得到的传热关系式,并与试验得到的数据进行对比。
当 试 验 工 况 为P=25 MPa,Qm=573 kg/h,tin,in=320 ℃时,得到的传热关系式对换热系数的预测值与试验值随Tb变化的趋势如图15所示。

图 15 传热关系式对换热系数的预测值与试验值变化趋势Fig.15 Variation tendency between the correlation empirical predicted value and experimental value
由图15可以看出,不同传热关系式得到的换热系数在偏离拟临界温度区域走势基本一致,可以比较准确地预测外管换热系数。当Tb处于拟临界温度区域附近时,物性剧烈变化,不同传热关系式对换热系数的预测差别较大,Mokry等[15]和Bishop等[16]所提出传热关系式的预测值与试验值的误差相对较小,但是仍然无法准确预测本试验中的外管换热系数,经对比发现二者的传热关系式均引入了密度比值修正因子以及管道入口效应。
由于诸多传热关系式均无法准确预测本工况下的试验结果,因此有必要针对本试验结果整理并提出一个外管传热关系式。该传热关系式基于Dittus-Boelter管道强制对流传热关系式,并引入了 ρb/ρw、管道入口效应 (1+2.4D/L),同时考虑到拟临界温度区域附近由水的比热容引起的换热系数急剧增加,加入了Cpb/Cpw,得到的传热关系式为
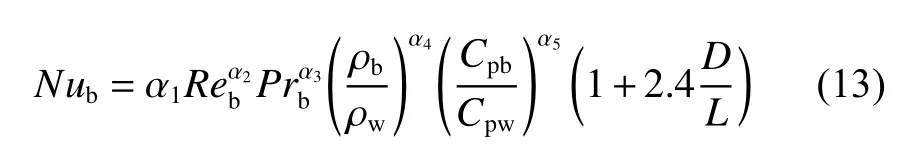
式中:Pr为普朗特数;Re为雷诺数;下标b表示主流温度,w代表内管外壁 温度; α1, α2, α3, α4和 α5为系数。下面对系数进行计算。
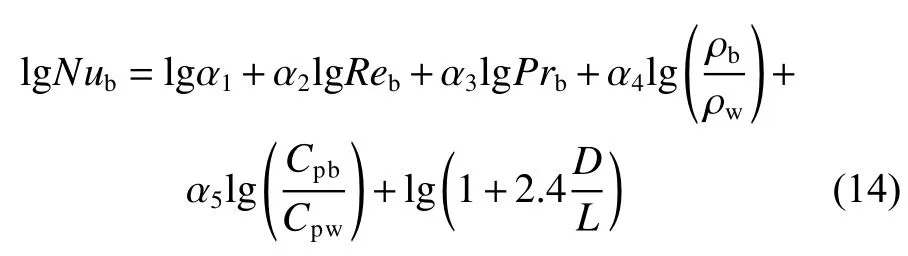
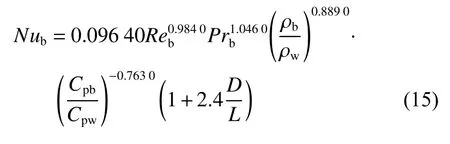
通过多元线性回归拟合,计算系数 α1~α5。本试验工况下的传热关系式为图16为本试验条件下,超临界水在套管换热器内实现流动传热时,由外管流体流动测量数据计算得到的NuE与提出的传热关系式得到的预测值NuP的对比结果。
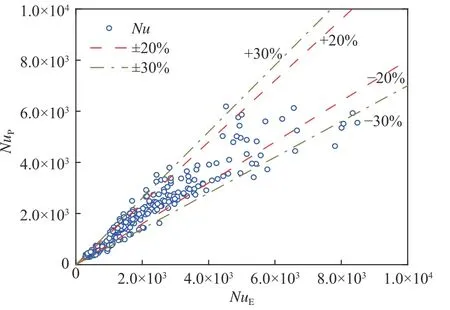
图 16 试验值NuE与预测值NuPFig.16 The experimental value NuE and predicted value NuP
由图16可知,在基于提出的传热关系式计算得到的数据中,92%以上的试验数据在±20%误差范围内。说明该传热关系式可以对超临界流体在套管换热内发生的强耦合传热进行有效预测,对于双超临界流体工况下的套管换热器设计具有一定的参考价值。
2.4.2 阻力关系式整理

基于Filonenko阻力关系式f=(alg(Re)+b)c,通过多元线性回归拟合,计算系数a,b,c,得到基于本试验工况下外管的阻力关系式为

图17所 示 为P=25 MPa,Qm=573 kg/h,tin,in=320 ℃条件下,该阻力关系式对套管换热器外管进出口压差 ΔP的预测值与试验值的对比。由图可见,采用阻力关系式预测的阻力系数比较准确,得到的进出口压差预测值 ΔPP与试验测量值ΔPE的误差最大仅为5.95%,可以有效预测超临界流体在环管内的流动阻力系数,有助于研究超临界流体在环管内的流动阻力特性。
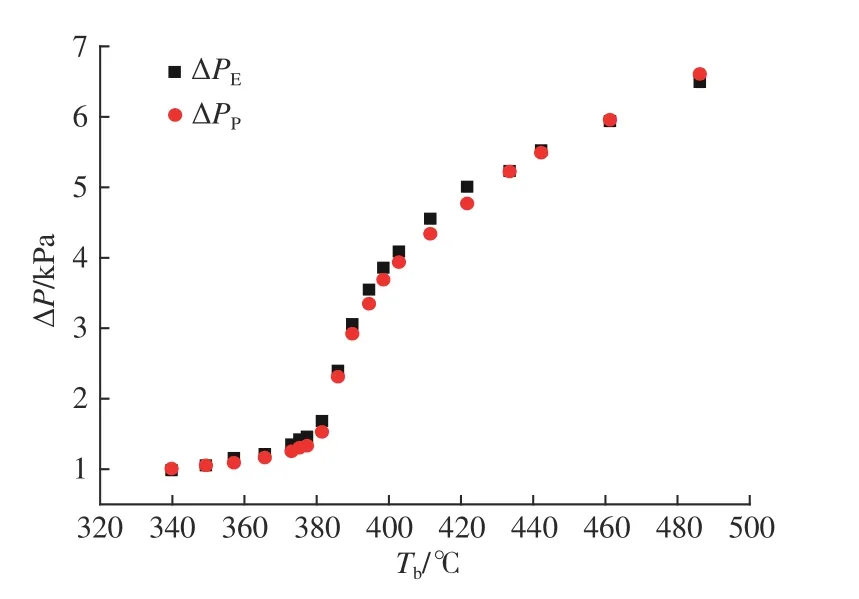
图 17 压差预测值与试验值Fig.17 The predicted value and testing value of differential pressure
3 结 论
通过超临界水在套管换热器内的流动与传热试验研究,分析了内管入口温度、管内质量流量和管内运行压力变化对流动传热的影响,得到以下结论:
1) 拟临界温度点附近物性参数的巨大变化是导致超临界水换热出现不同于平常换热现象的主要原因。水在套管换热器内流动时,套管换热系数随着主流温度的升高呈抛物线变化。而拟临界温度区热物理性质急剧变化所引起的截面上的径向密度梯度导致了浮力效应,随着超临界流体流量减小或热负荷增加,浮升力效应逐渐增强,强制对流换热逐渐转变为混合对流换热。因此,当主流温度低于拟临界温度时,外管换热系数随内管入口温度的增大而增大;当主流温度高于拟临界温度时,浮升力效应不显著,因此外管换热系数几乎与内管入口温度无关。
2) 套管换热系数随质量流量的增加略有增加,外管换热系数几乎与质量流量无关。可能的原因是,内管侧和外管侧的质量流量总是相等的,并且一侧会抵消另一侧对传热的影响。
3) 外管换热系数在拟临界温度区达到峰值。随着运行压力的增加,峰值换热系数减小并向高温侧移动。套管换热系数峰值对应的温度与拟临界温度之间存在差异,且差异随压力的增大而增大。传热截面上的温度梯度和热物性,特别是密度的变化是产生这种现象的主要原因。
4) 本文通过对试验数据进行研究分析,提出了一个考虑了密度、比热容以及入口效应修正的传热关系式,且与本文的试验结果吻合良好,同时,还得到了环形外管内超临界流体的流动阻力关系式,有助于环管内的流动阻力特性研究。

