基于粒子群优化径向基函数神经网络的电力负荷预测*

关书怀, 沈艳霞

(江南大学 物联网技术应用教育部工程研究中心，江苏 无锡 214122)

0 引 言

电力负荷预测是电力系统经济运行的基础，对电力系统规划以及降低电力生产成本意义重大[1]。目前，负荷预测可以分为三种类型，即短期预测、中等期限预测和长期预测[2]。与短期负荷预测不同，长期负荷预测更易受许多不确定因素影响，预测难度大[3,4]。针对长期负荷预测，国内外学者已经进行深入研究，预测方法主要包含参数方法如回归预测、时间系列和灰色理论等[5]及人工智能方法。如文献[6]应用灰色理论建立预测模型，过程计算量较小且精度较准确。人工智能方法包括神经网络(neural network,NN)和动态模糊综合评价等[7]。其中神经网络作为一种最受欢迎的预测模型已被广泛应用于处理相对复杂的关系[8]。文献[9]提出基于大数据和粒子群优化(particle swarm optimization,PSO)反向传播NN(back propagation NN,BPNN)短期电力负荷预测，建立针对海量电力数据的短期负荷预测模型，但计算量较为繁琐。文献[10]针对短期电力负荷预测问题，提出了一种基于PSO算法的BP-NN预测模型跳出局部最优，增强了粒子的全局寻优能力，但预测模型的泛化能力不甚理想。相比于多层前馈网络(multilayer feedforward network,MFN)，径向基函数(radial basis function,RBF)由于其学习规则简单便于计算实现，具有良好的泛化能力，能够在一个紧凑集和任何精度下，逼近任何非线性函数[11]。文献[12]提出基于RBF-NN分位数回归概率密度预测方法，得出未来一天中任意时期负荷的概率密度函数，获得比点预测和区间预测更多的有用信息，实现了对未来负荷完整概率分布的预测，但该方法在RBF-NN易陷入局部最佳值这一问题上未得到充分解决。在预测模型初始化阶段文献[13,14]中采用了模糊聚类EM算法，却加重了聚类过程的计算量并降低了聚类效率。文献[15,16]中针对电力负荷预测结构的参数寻优采用蚁群优化(ant colony optimization,ACO)算法，但存在搜索时间较长，易陷入局部解进而停滞。文献[17]所采取的人工蜂群(artificial bee colony,ABC)算法虽有较快的收敛速度，但易陷入局部最优值。

为了能够有效地跳出模型训练过程中的局部最优点，加速模型训练速度，本文使用K-means聚类算法将训练集聚类以加快模型结构学习，在模型的参数寻优阶段集成粒子群优化算法，采用自适应梯度下降策略二次训练模型，从而使模型跳出局部最优解，提升预测精度以及泛化能力。通过仿真验证所提出的预测模型精度及泛化能力优于传统的RBF,ACO-RBF,ABC-RBF-NN。

1 负荷数据的聚类分析

电力负荷预测的关键是负荷相关数据的分析，准确地从中挖掘出负荷发展规律。考虑历史负荷数据是众多时间序列，通过负荷聚类将变化特性相似性高的负荷归聚同类，将相异性强的负荷聚于不同类，将变化特性相似的负荷集聚研究不仅有利于挖掘类型负荷的增长规律，也有利于负荷影响因子相关性分析，进而通过建立准确的预测模型，实现负荷的精确预测。

本文在电力负荷预测模型中集成了K-means聚类算法。在训练前，先将电力负荷数据训练集的所有特征归一化到[-1,1],之后用K-means聚类算法将训练集聚类为 个集群，具体K-means聚类步骤如下：

1)确定聚类簇数目K以及训练集样本数目M={M1,M2,…,Mk}。

2)随机选定K个电力负荷数据样本的特征作为高斯激活函数的初始中心位置。

3)计算电力负荷数据集中每个样本到初始聚类中心的欧氏距离，并将样本与距离最近的激活函数打上相同标签。

4)重新计算每个聚类簇负荷数据的各个特征平均值，以更新每个集群中心

(1)

式中Cj为第j类聚类簇的聚类中心，Nj为第j类聚类簇的样本数目，Mj为第j类聚类簇的第j个样本。

5)判断电力负荷预测系统的迭代数目若未达到最大值，则重复步骤(3)和步骤(4)，直到不再更改聚类簇的中心位置，否则迭代停止。其中每个簇的中心作为隶属函数的中心，簇之间的最小距离作为隶属函数的宽度。

2 RBF-NN电力负荷预测模型

基于RBF-NN的电力负荷预测模型如图1所示，包括3层结构：输入层、隐含层及归一化层、输出层。

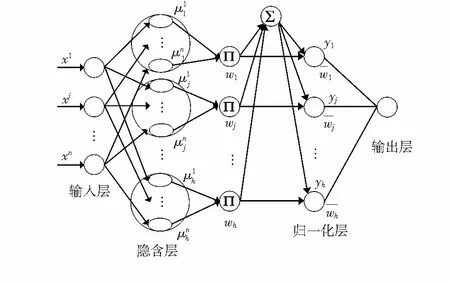
图1 RBF-NN电力负荷预测模型

输入量为X=[x1x2…xn]T，其中n为输入特征的维数，xi表述样本中的第i维特征，包含年、月、日、小时、星期、温度等参量。

隐含层及归一化层中神经元激活函数由RBF构成。隐含层的输出为非线性激活函数xi,bj,cj构成

(2)

式中bj为一个正的标量，表示高斯函数的宽度；m为隐含层的节点数量。

第j个节点的激活强度为

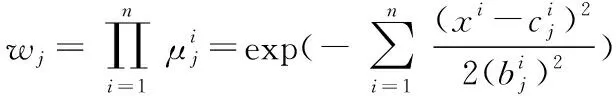
wj=exp(-md2(j))

(3)

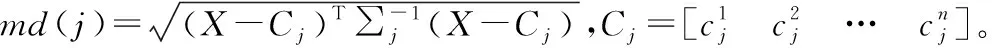
(4)

3 基于改进PSO算法的模型参数寻优

为了克服模型训练过程中的局部优化问题，使得电力负荷预测值与期望值的差值尽可能缩小，可以根据模型的实际输出和预测输出之间的误差优化中心参数c和方差b的选取，提高模型的精度。为此本文在模型的参数寻优阶段集成了PSO算法。

PSO的过程是先随机初始化一组粒子，然后通过迭代搜索最优解。在每次迭代中，粒子都是通过对粒子的最优解pbest和整个群的最优解gbest两种粒子的追踪来更新它们的位置。设有n个粒子和D维搜索空间，则追踪的数学表达式如下

Vid(t+1)=w0Vid(t)+c1r1(Pid-Xid(t))+

c2r2(Pgd-Xid(t))

(5)

Xid(t+1)=Xid(t)+Vid(t+1)

(6)

式中Xi=(Xi1,Xi2,…,Xid),Vi=(Vi1,Vi2,…,Vid)为粒子的当前位置和当前粒子的飞行速度。Pi=(Pi1,Pi2,…,Pid)为pbest，表示当前粒子的最优位置Pg=(Pg1,Pg2,…,Pgd)为gbest，表示整个粒子群的最优位置。w为惯性因子，是一个非负数。c1,c2为学习率，r1,r2为两个非负数， 是随机指定的，范围是[0,1]。Vid∈[-Vmax,Vmax],Vmax为粒子速度的最大限定值。t为当前算法的迭代次数。

采用PSO RBF-NN模型参数中心参数c和方差b的步骤如下:

步骤1 对RBF-NN神经网络模型初始化参数和权重。

步骤2 建立RBF-NN模型，根据输出误差指导学习过程，将训练所得电力负荷预测值与期望值之间的误差作为粒子群的适应度函数。

步骤3 更新参数和权重。然后更新粒子的速度和位置。

步骤4 确定粒子群的迭代次数是否达到最大。若是，则计算RBF-NN模型的最优参数。如果没有，回到步骤3。

步骤5 二次判断，即确定RBF-NN梯度下降的迭代是否达到最大值。如果达到最大值，建模过程结束。否则，重复步骤5。

尽管使用了启发式的PSO算法，但是粒子的寻优过程还是有可能会由于动量不足而陷入局部最优的困境，所以，在步骤5的梯度下降算法中引入自适应学习率调整机制：

a.当RMSE(t)≥RMSE(t-1)时，那么

γ(t+1)=jsγ(t),η(t+1)=0

(7)

γ(t+1)=zjγ(t),η(t+1)=η0

(8)

γ(t+1)=zjγ(t),η(t+1)=η(t)

(9)

式中t为迭代次数，js和zj分别为减少和增加因子；δ为基于均方根误差(root meas square error,RMSE)的相对指标的阈值；因此，需要满足如下条件(10)

01

(10)

4 仿真验证与结果分析

为验证以上模型预测精度的可靠性，本文选取澳大利亚电力公司公开的电力负荷数据集进行算例分析。基于PSO算法优化RBF-NN的负荷预测流程图如图2所示。

图2 电力负荷预测流程图

图3所示采用PSO算法优化的RBF-NN模型的最小误差演变曲线，模型适应度函数在35次迭代更新后收敛。PSO-RBF-NN模型的负荷预测效果如图4所示，相较于传统RBF预测效果，PSO-RBF-NN模型在电力负荷一年中的预测效果更符合真实负荷。

图3 采用PSO优化的RBF-NN模型的最小误差演变曲线

图4为PSO-RBF和传统RBF预测效果图，可见PSO-RBF在任意时段的预测精度均有发幅度提升。

图4 模型与传统RBF-NN负荷预测性能比较

图5为PSO-RBF和ABC-RBF预测效果图，可见PSO-RBF在负荷峰值区域预测更加精准。

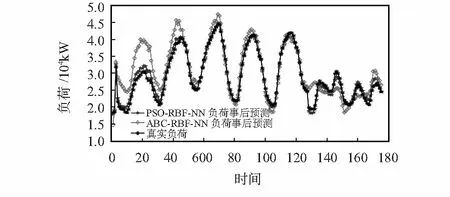
图5 模型与ABC-RBF-NN负荷预测性能比较

图6为PSO-RBF和ACO-RBF预测效果图，可见PSO-RBF预测精度不会随时间增长而受影响。图4～图6中不同NN模型在训练前对数据集均进行K-means算法聚类，依从单一变量原则，证明PSO-RBF的预测精度。

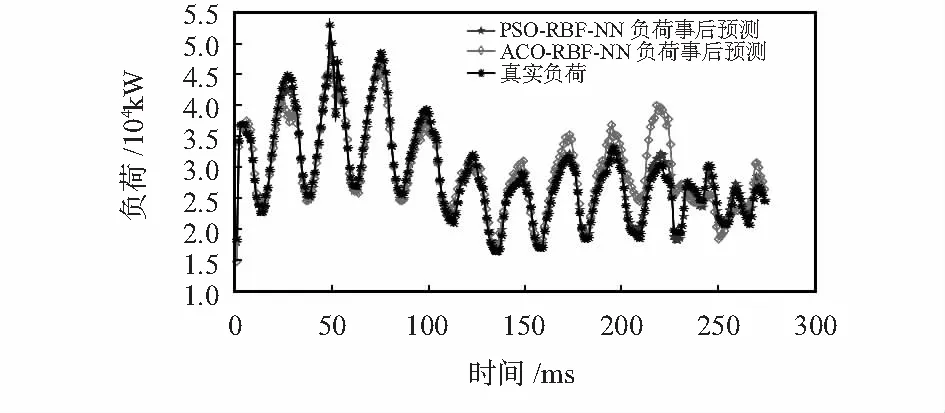
图6 模型与ACO-RBF负荷预测性能比较

表1为基于PSO优化的预测模型与其他预测模型的标准误差比较。 由表1可以看出， PSO-RBF的训练均方根误差(标准误差)为0.068，远小于传统RBF训练的标准误差0.094，与基于ACO和ABC的RBF预测模型训练标准误差值0.079和0.073相比较，预测精度更加准确。PSO-RBF的网络节点数相较其它网络类型更少，故计算量更少。

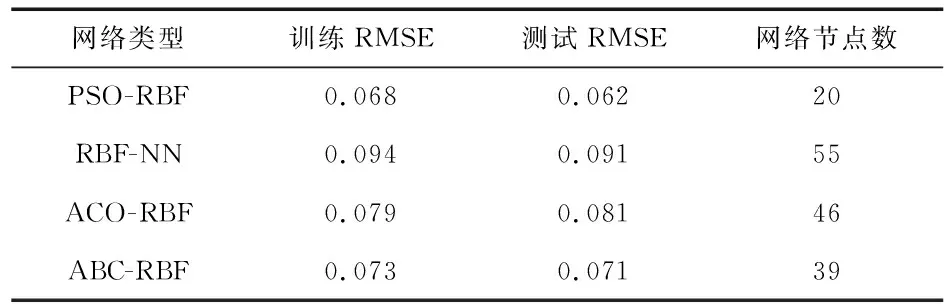
表1 标准误差比较

由仿真图4～图6以及表1可以看出，相较于RBF-NN,ABC-RBF,ACO-RBF，PSO-RBF-NN的预测结果更加贴近于真实负荷结果，证明了改进后的系统可以有效跳出因梯度下降而陷入的局部最优解这一问题，从而具有更高的预测精度和泛化能力。

5 结束语

本文针对时间尺度较长这一前提，细化了训练模型的过程中建立新的模糊规则的情况。针对RBF预测模型因梯度下降进而陷入局部最优解这一问题，采用PSO算法对模型参数寻优，使模型跳出局部最优解，提高了影响因素与负荷水平的相关性。相对于传统的长期负荷预测模型，建立了更加完善的预测模型，并通过实际负荷数据进行了验证，结果表明：相比于传统RBF-NN预测模型，本文所提出的预测模型具有更高的预测精度和泛化能力。