基于图像自相似结构的视频图像插值算法研究*

向 豪, 孙 冬, 高清维, 卢一相

(安徽大学 电气工程与自动化学院,安徽 合肥 230601)

0 引 言

视频插值是视频处理中的一个重要研究方向,主要用于精确恢复低分辨率视频图像中的某些未知像素信息。随着监控系统、遥感测控、自动驾驶等领域中视频图像技术的广泛应用,人们对高分辨率视频图像的需求越来越高,但是传统的视频图像插值算法很难恢复原始高分辨率图像中的细节信息。

目前研究者已提出大量插值算法用于视频图像高分辨率重建,其中应用最多的是基于核函数的插值算法,如双线性、双立方和B样条插值算法等[1,2]。这类算法思想简单,主要是利用一个特定核函数对目标点周围的像素值进行加权,从而计算出该目标点的像素值,具有较低的算法复杂度和较快的运行速度。但该类算法将整个图像看作一个整体,没有区分图像中各个像素表达的特征信息,导致重建的高分辨率图像包含的高频信息较少,锯齿和模糊效应较为严重。

图像的细节主要集中在图像的边缘、纹理等高频区域,人类视觉系统对这些内容敏感度较高,因此准确重建图像的细节对视频图像的插值极为关键。文献[3～5]研究了基于边缘检测的图像插值方法,即沿着图像的边缘方向进行插值,保证了边缘不被模糊化,提升了插值后的视觉效果。Li X在文献[6]中提出了隐式利用边缘信息插值图像的算法,其通过自适应回归模型,来估计低分辨率图像像素间的协方差关系系数,再根据几何对偶性假设,计算未知高分辨率图像像素,因此具有较好保留边缘特性的优点,但是当图像结构复杂或者有噪声干扰时容易造成边缘模糊和人工痕迹。

基于贝叶斯理论框架的图像插值算法也研究甚多[7～9],该类方法首先将图像的边缘结构信息作为先验知识,然后通过正则化方程来确定高分辨率图像的最大后验概率。该方法在降低未知像素自由度的同时,还可以恢复插值后图像的边缘结构以及抑制伪影的产生,从而建立更清晰的高分辨图像。但是该方法难以准确构造约束项,优化求解也比较复杂,给后继的具体实现带来了困难。

近年来,许多学者将深度学习理论也引入到插值算法中。文献[10～12]提出利用卷积神经网络去学习低分辨率图像与高分辨率图像之间的映射规则。首先将低分辨率图像送入神经网络来拟合图像中的非线性特征,然后根据先验知识设计损失函数,通过大量数据训练来寻求该函数的最优解,最后输出高分辨率图像。考虑到不同的放大因子需要分别对模型进行大量的数据训练,因此该方法不能对图像进行任意放大,此外利用该方法重建后的图像通常过于平滑,一定程度上还会丢失一些重要的高频信息。

大多数自然图像都具有较强的空间冗余结构,Sun D在文献[13]中根据这一特性提出了信号的非局部自回归(non-local auto regressive,NAR)算法。NAR利用图像中的相似性先验,指出了位于图像中不同位置的局部图像块之间的相似关系,再根据不同的采样网格在待插值图像块的非局部区域来建立局部字典,然后通过相似性关系对字典进行训练,形成K个与该图像块相似的图像块,通过对应的采样网格对其进行下采样,最后将上述图像块互补拼贴成高分辨率视频图像。NAR算法很好地解决了边缘和纹理等高频信息恢复较差的问题。

由于视频是一幅幅视频图像的集合,相邻视频图像同一位置的像素值变化不大,因此本文在NAR的基础上进行了改进,利用视频帧间和帧内冗余的相似性结构来对要恢复的低分辨率视频图像进行插值。实验表明,本文算法取得了比NAR更好的图像插值效果。

1 主要思想

由于视频图像帧间和帧内存在大量的相似性结构,故图像中的每个图像块均可由K个不同位置处的图像块进行线性组合,如图1(a)所示,此时图像块方程为

s=Gisj+e≈Gisj

(1)

式中Gi为退化矩阵,e为残差,sj为与当前待插值的图像块相似的图像块,本文的主要工作也就是对sj的寻找。

图1(b)中方块si为当前视频图像中待拼贴的图像块,以si为中心,设立边长为W的窗口,同理在当前帧的前后各L帧(图1(b)中只选用了前后各一帧作为参考图像)中确定相同位置及大小的搜索框,作为si相似父块的搜索区域,根据不同的下采样网格,将该区域中的图像块以列堆叠的方式放进三个不同的字典Sp(00,01,10)中,依次计算三个字典中的每个列向量与si(用列向量表示)的相关程度,对所得结果按照大小顺序进行排序,保留前K个最大相关度所对应的列向量,用以对si进行线性表示,因此得到三个si的近似估计,再将上述三个图像块根据相应的采样网格进行下采样,最后将下采样后的低分辨率图像互补拼贴成高分辨率视频图像块(如图1(c)中箭头所指的最后一个图像块所示)。

图1 算法框架

2 算法设计

2.1 互补拼贴图像块之间的关系

首先,确定下采样网格

Gi=G11={(x,y)│x=2a-1,y=2b-1}a,b∈Z

(2)

式中i为待插值图像块的左上角坐标(如G11用来对左上角坐标横纵坐标均为奇数的图像块进行下采样)。同理,可以定义其他下采样网格G10,G01和G00。

设置与采样网格G对应的退化矩阵,用于将sj以隔行隔列抽取的方式映射成低分辨率图像块,再将得到的低分辨率图像块拼贴成高分辨率图像块。

2.2 高分辨率图像sj的查找

从当前视频图像中取出左上角坐标为(xi,yi)处的图像块si,建立以si为中心,宽度为W的窗口。同理,在当前视频图像的前后L帧中确定相应位置及大小的搜索框,作为查找与si相似的图像块的候选区域。在每个搜索框中寻找式(2)中的三种采样网格对应的图像块,放进相应的字典Sp(p=00,01,10)中,然后对字典中的原子进行训练,本文使用最大归一化內积的方式来判别图像块Spj(Sp中的原子)与图像块的si的相似程度

(3)

则,si在Sp下的系数表示为

(4)

(5)

式(5)是一个凸优化求解问题,可以得到其封闭解

(6)

因此,得到插值方程

(7)

当所有的图像块拼贴完成以后,用式(7)对si进行更新,然后将更新后的高分辨率视频图像块作为初始图像块,紧接着进行下一次的迭代。

2.3 插值算法

由于高分辨率视频图像sj往往是未知的,所以为了使式(7)具有实际意义,本文将所有视频图像序列进行下采样处理,得到低分辨率视频图像f=Ds,再采用传统的双立方插值算法还原成高分辨率图像sj,然后为sj确定自相似性图像块,代入到上式中可以得到

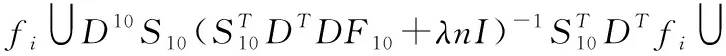
(8)

该视频图像中所有的图像块均采用互补拼贴处理,并用式(9)对si进行更新,得到

(9)

视频图像插值算法过程如下：

准备阶段：

1)将低分辨率视频切割成帧图像集,再将该视频图像集逐帧进行双立方插值,还原至原图像大小,得到高分辨率视频帧的近似估计。

2)设置参数：块尺寸n,窗口W,参考帧数L,迭代次数p。

插值阶段：

1)创建块尺寸大小为n的滑窗,步长设置为1,对待插值的视频图像进行分块处理,将切割后的图像子块以列堆叠的方式放进字典sm中,同理对参考帧也进行相同分块操作,放进字典Smj(j=1,2,3,…)中。

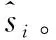
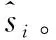
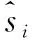
5)将输出的高分辨率图像进行连接,组合成高分辨率视频。

输出：高分辨率视频。

2.4 参数选取

1)参考帧数L的选取。以待插值的视频图像为中心,前后各L/2帧作为参考,实验结果表明,在一定范围内随着参考帧数的增加,要插值的图像块能够利用的有用信息越多,重建的效果也越好,但参考帧数选取过多容易产生过拟合效果,插值质量会有所下降,时间也是线性增加。本文选取L=2。

2)图像块尺寸n大小的选取。对于不同分辨率的图像,如果块尺寸选择过大会给非局部自相似性图像块的查找带来一定的难度,而过小的块尺寸又不能提供足够的有效像素信息来表示图像的局部特征,同样会影响插值图像的质量。本文将块尺寸设置为n=8。

3)窗口W大小的选取。确定以si为中心,宽度为W的窗口,在前后多帧图像中确定同样大小及位置的搜索框,在这些区域寻找图像si的相似图像块,过大的窗口会增加计算量,对插值的性能有一定的影响。本文将Foreman和Ice视频序列的窗口的宽度分别设置为W=14和W=36。

4)迭代次数p的选取。迭代次数对插值的算法来说影响并不是很大,但是如果p选择过大,将增加本文算法的运行时间,故本文选取p=4。

3 实验与分析

为了验证本文所提出的视频图像插值算法的可行性,本文通过选取2组标准视频序列Foreman(288×352)和Ice(576×704)进行插值重建,将重建后的结果和原始视频图像进行比较,采用PSNR和SSIM对插值后的高分辨率视频图像进行客观评判。实验硬件平台为Intel®CoreTMi5-7300HQ@ 2.5GHz,8G运行内存；软件平台为Windows 10教育版,MATLAB 2016b。实验选取参数为：n=8,W=20,p=4,L=2。

首先对高分辨率视频进行下采样,以获取低分辨率视频图像(144×176和288×352),再使用双立方插值、NAR算法以及本文算法来对上述低分辨率视频图像进行插值。

图2分别显示了用本文算法对视频序列Foreman和Ice的第4帧视频图像的插值结果,从图中可以看出,本文算法能够对图像的边缘和纹理等高频信息进行精准的恢复,重建后的图像较为清晰,没有模糊和锯齿效应。

图2 Foreman和Ice第4帧低分辨率视频图像及部分放大图像细节

从图3中可以看出双立方算法在图像低频部分能够得到较为平滑的插值结果,但是在图像的边缘区域显得格外的模糊,而且锯齿效应严重(如图中墙壁上的斜杠以及帽子的边缘部分)。因此,可以看出双立方插值并没有有效恢复图像的高频细节信息,从而图像插值后的结果不是很理想。

图3 Foreman第5帧低分辨率视频图像及各算法插值结果

图4中可看出,NAR插值算法和本文所提出的算法具有类似的主观视觉质量,这两种方法都充分利用了图像所包含的空间冗余结构信息,使得图像中的平坦区域具有光滑的效果,并且对于图像边缘和纹理等高频信息较为丰富的部分也能实现较好插值重建,但是从图中男子手握拳头这个细节可以发现,使用本文算法进行插值得到的图像在边缘的恢复上相较NAR算法来说实验效果更优,主要原因是本文插值算法在NAR算法的基础上结合相邻图像之间的空间冗余性进行插值,使非局部相似图像块的查找范围更广,因此也具有更加满意的插值效果。

图4 Ice第5帧低分辨率视频图像及各算法插值结果

从表1可以看出在PSNR和SSIM两个评价指标下,本文方法均优于双立方插值算法及NAR算法,且随着图像中的高频信息的增多,这种优势就会越明显。

表1 Foreman和Ice中相应视频图像插值结果的PSNR和SSIM客观质量对比

4 结 论

基于视频图像间存在的空间冗余信息,本文在NAR模型的基础上构造了一个具有闭合解的数学模型。该模型利用了视频图像帧间的自相似先验,将待插值图像块相似父块的搜索区域拓展到相邻多帧图像上,使该图像块表征的像素信息更为精确,恢复的高分辨率图像也愈加清晰。实验表明：在PSNR和SSIM两个评价标准下,本文方法在处理边缘丰富的图像时效果明显优于双立方和NAR方法。进一步研究将该算法拓展应用于视频编解码。因为现有高分辨率视频传输时需要较大的码率,然而较大的码率需要足够的带宽作为支撑,成本消费较大,所以，可以考虑先将高分辨率视频进行数据压缩,即下采样至低分辨率视频,再进行视频的编解码,最后通过本文算法对该视频进行超分辨率重建,获取较高质量的输出视频。