基于视觉测量的Tripod机器人运动标定方法研究*

杨继东， 陶金池， 覃 畅

(重庆大学 机械工程学院，重庆 400044)

0 引 言

精度问题作为并联机器人重要的性能指标之一，在生产应用中往往通过运动学标定来提高精度[1,2]。标定的主要过程包括建立误差模型、误差测量、参数辨识和误差补偿。并联机构的标定方法一般分为自标定法和外部标定法。自标定法[3]是通过内部传感器或者施压外约束获得测量信息，可以实现在线标定，但无法提供坐标系间的未知刚体信息；外部标定法通过外部传感器测量末端位姿误差，通过辨识模型得到补偿参数。

因为测量信息直接决定辨识模型的输入，因此测量方法是标定过程中极其重要的一环。通常用于精度标定的测量系统有激光跟踪仪、经纬仪、球杆仪等，视觉测量因其经济便捷的特点也作为新兴的测量系统用于标定。

文献[4]通过建立零点误差映射模型，采用激光跟踪仪对混联机器人进行快速标定；文献[5～7]采用的方法是将标定板固定在机器人末端动平台上，通过运动空间外固定的摄像机拍摄动平台的标定板从而得到动平台相对于摄像机的位姿，但该方法摄像机视野固定，易受其他运动结构遮挡干扰，不适用于所有机器人；文献[8]提出一种基于摄像机拍摄立体靶标序列图像信息，建立空间刚体位姿与其二维图像映射关系模型辨识末端位姿；文献[9]通过安装在机器人末端的摄像机随机器人转轴转动拍摄标靶，利用得到的摄像机光心坐标拟合圆得到机器人轴线方程。

为实Tripod机器人生产线上的标定与视觉检测抓取相结合，本文通过采用视觉测量的方法实现机器人的运动学标定研究。

1 结构分析与误差模型建立

1.1 结构分析

图1(a)为Tripod机器人的三维模型。该机器人主要由静平台、三组支链、动平台组成，每组支链包括交流伺服电机、电缸、滑块、平行四边形从动臂等。电缸与静平台于一定角度固定，滑块连接电缸与平行四边形从动臂，从动臂两端通过虎克铰链分别连接滑块和动平台，由电机带动电缸滑块移动达到控制动平台的移动。

其自由度可由Kutzbach-rubler公式计算如下

(1)

式中n为运动件数，g为运动副数，fi为每个运动副具有的自由度数。

因此对于该Tripod机器人自由度

F=6×(8-9-2)+15=3

(2)

固该机器人具有3个自由度，动平台末端位置能够在动作空间内做3个方向平动，达到任意期望位置。

1.2 建立误差模型

为使机器人结构更直观且更容易建立运动学误差模型，将该Tripod机器人结构简化，并定义各个关键点位坐标系，如图1(b)所示。

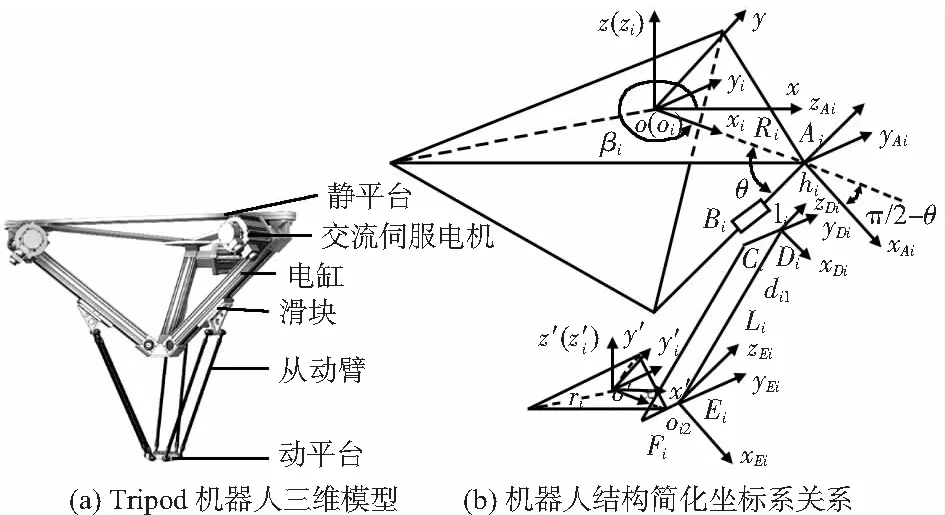
图1 Tripod机器人三维模型及其结构化坐标系关系

在为等边三角形的静平台中间建立基坐标系O-XYZ，Y轴指向第二条支链静平台与电缸连接的中点，Z轴垂直于静平台参考基准面竖直向上，X轴方向满足坐标系右手定则；建立动平台坐标系O′-X′Y′Z′,方向均与静平台相同，坐标系原点O′位于动平台等边三角形中点；设定一个零点位置坐标系O″-X″Y″Z″，坐标系原点位于机器人动平台实际的初始末端位置的等边三角形中点，坐标系方向与基坐标系均相同。

Tripod并联机器人动平台末端位置误差可分为两类，一类是结构性误差， 因机构的实际参数与设计值不一致而导致的误差，比如加工、装配、零点误差等，这类误差可以通过运动学标定减缓或消除；第二类误差是随机性误差，如热变形误差、传感器检测误差等，这类误差不能通过运动学标定进行消除。固建立误差模型中，只考虑第一类的结构性误差。根据对该Tripod机器人系统结构的简化和分析，主要的各个构件参数和误差表示及尺寸如表1。

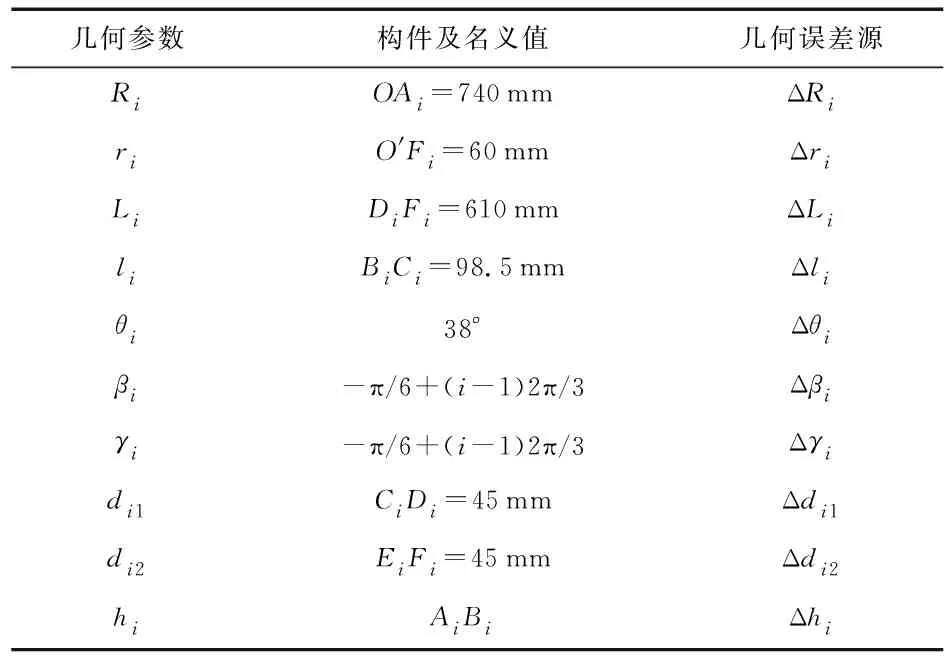
表1 构件信息表

其中，ΔRi，Δri表示静平台与动平台分别的加工误差导致其外接圆半径的误差，ΔLi表示平行四边形从动臂杆长的加工误差，Δli表示滑块的加工误差，Δθi表示电缸与静平台装配的角度误差，Δβi表示电缸安装在静平台的结构角误差，Δγi表示从动臂安装在动平台的结构角误差，Δdi1，Δdi2表示从动臂虎克铰链中心距误差，Δhi表示零点误差。

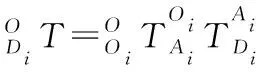
(3)

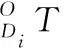
(6)

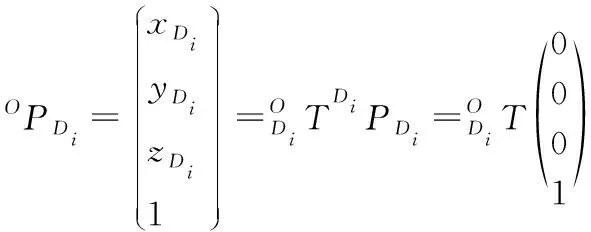
(7)

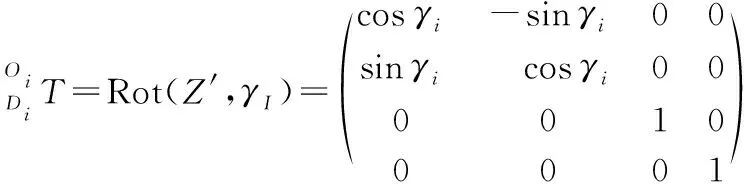
(8)

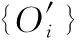
(9)

考虑到该Tripod并联机器人动静平台的位置关系中，每一条支链存在杆长约束条件|DiEi|=Li，上述已给出基坐标系下Di，Ei的坐标，可建立如下方程组

(10)

将Di,Ei的坐标代入式(10)，是关于参数Ri,ri,li,θi,βi,γi,di1,di2.Li,hi,x,y,z的方程组，用隐函数的形式表示为

fi(Ri,ri,li,θi,βi,γi,di1,di2·Li,hi,x,y,z)=0

(11)

设机器人关节构件的参数集合为q={Ri,ri,li,θi,βi,γi,di1,di2·Li}，输入参数集合为p={hi}。在运动学正解中，参数集合q,p已知，设正运动学方程表示为P=F(q,p)，代入方程组(11)可求得末端位置P=[xyz1]T；在运动学逆解中，已知参数集合q和末端位置P，依据滑块行程的约束条件，代入方程组(11)可求得唯一解集合p。

对式(11)进行微分，得到全微分方程

i=1,2,3

(12)

将式简化为矩阵形式

ε=H-1KΔ

(13)

式中

ε=[dxdydz]T

Δ=[dRidridlidθidβidγiddi1ddi2dLidhi]T

式中ε为末端位置误差，H为Tripod机器人的逆雅可比矩阵，K为误差系数矩阵，与具体的机械机构相关的，Δ为各项几何误差源集合。

为了研究零点误差的运动学标定，将其他参数误差都假设为零点误差，均累积到零点误差中，提取零点误差与末端位置误差的映射关系得到零点误差模型

ε=H-1KH

(14)

2 误差辨识与测量

对于并联机器人参数的辨识方法，文献理论和实验证明，并联机构可以通过检测末端沿任意单轴的相对位置误差和初试位形下的姿态误差便可识别出几何参数[10～13]。由此，本文实验中，对z平面的末端位置检测，采用摄像机测量Tripod机器人末端位置以及建立辨识模型以辨识零点误差。

建立摄像机坐标系{OC}，坐标系原点OC位于摄像机光学中心；世界坐标系{OW}，即标定坐标系，坐标系原点位于标定板平面坐标系原点。为各坐标系之间坐标转换带来的误差，使用相对坐标来定义残差。如图2，操作机器人动平台移动到某两个不同位置，根据机器人正解模型，可以得到基于基坐标系{O}的动平台位置矢量，分别为ni和nj。摄像机标定得到精度较高的外参以实现世界坐标系{OW}与摄像机坐标系{OC}之间的刚性变换

PC=RPW+T

(15)

式中PW为世界坐标系下点P的坐标，R为R(α，β，γ)一个旋转矩阵，三个旋转角度分别为绕摄像机坐标系z轴旋转角度γ，绕y轴旋转角度β，绕x轴旋转角度α，T为一个平移向量(tx,ty,tz),PC为摄像机坐标系下点P的坐标。

由上式方法可测量出在运动空间中世界坐标系下摄像机对应的坐标矢量Ni和Nj。实验中摄像机随动平台在测量平面内移动，摄像机与机器人动平台在测量过程中无相对位移，因此，可以视为测得的摄像机坐标系在标定坐标系下的相对位移即动平台在基坐标系下的相对位移。

图2 视觉测量原理

构造两点间测量值相对坐标与正解模型下两点的实际输出的残差

γij=|Ni-Nj|-|ni-nj|

(16)

式中Ni，Nj为机器人在i位置的视觉测量坐标；ni,nj为机器人在i位置的正解模型实际坐标ni=f(pi+dp,q)。

由非线性最小二乘法构造如下函数

(17)

采用Levenberg-Marquart算法得到最优化结果dp。

3 误差补偿与实验验证

3.1 运动学标定前位置精度检测

实验使用的Tripod机器人工作空间为φ600 mm×200 mm的圆柱空间，根据越靠近工作空间边界，误差反映越明显的特点,同时测点选取还需要考虑到均匀布满整个工作空间的原则，因此本文对z=800 mm和z=900 mm平面进行检测，测点选取采用每个平面内边界外圆圆心形成的三个半径公差为200 mm的同心圆，每个平面25个测点，如图3所示。

图3 测点分布

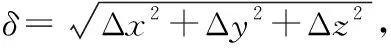
图4 测点误差分布(标定前)

3.2 摄像机标定

摄像机选用大恒的MER—125—30GM—PS数字面阵相机，在进行测量实验之前，需要通过内参标定得到精确的相机的内部参数。由Halcon与MATLAB联合编程，得到摄像机的内部参数。

表2 摄像机内部参数表

测量流程：1)将标定板置于机器人下方的工作台上，使用水平仪将工作台置水平；2)采用专用装夹工具固定摄像机于机器人末端位置，保证摄像机于工作台水平；3)控制机器人分别在z=800 mm和z=900 mm两个平面运行到25个测点位置，记录机器人每个位置的坐标名义值，并拍摄标定板图片；4)采用Halcon和MATLAB软件联合编程程序，通过拍摄图片，求得各个测点位置相对于标定坐标系的外参，得到测量值；5)将数据代入辨识模型求得零点误差Δhi,i=1,2,3。

对测点进行测量并通过辨识，得到平均零点误差如表3所示。

表3 零点误差辨识表

3.3 误差补偿

本次实验补偿方式采用修正系统输入，在不存在任何误差的情况下，f(x)表示机器人正解模型，f-1(x)表示机器人逆解模型，固机器人正解可表示为P=f(q0,p0)=f(q0,f-1(P0,q0))，实际上机器人存在几何参数误差，因此实际的机器人正解模型应写为

P=P0+ΔP=f(q0+Δq,p0)

=f(q0+Δq,f-1(P0,q0))

(18)

采用修正系统输入的补偿方式即修正输入参数p0使得

P=f(q0+Δq,p0+Δp)

=f(q0+Δq,f-1(P0+ΔP,q0))

(19)

具体的补偿流程如图5所示。

图5 误差补偿流程框图

采用该补偿方法将辨识模型的结果作为反馈，经过修正输入后，再次检测Tripod机器人末端位置误差，同样重复标定前的精度检测步骤，使用相同的激光跟踪仪检测工作空间内规划的两个平面内分别的25个测点，由两平面测点的测量结果得到标定后的平均位置误差为0.488 5 mm，最小位置误差为0.257 8 mm，最大位置误差为0.741 4 mm，如图6所示。

图6 测点误差分布(标定后)

通过对本文机器人的误差映射模型的建立、参数辨识、测点规划以及误差补偿，仅考虑零点误差进行运动学标定，使用传统的激光跟踪仪测量方法对标定前后精度进行验证，由测量结果表明，采用所提出的视觉测量方法，使机器人末端位置平均误差从0.9 mm左右提高到0.4 mm左右，使得机器人标定精度得到有效提高。

4 结 论

1)运用解析法，根据Tripod机器人的几何参数和运动学模型，合理建立坐标系关系，构造出误差映射模型并由此简化出零点误差映射模型；2)本文提出一种视觉测量方法，使用摄像机标定原理测量两测点间的相对位置，建立参数辨识模型以得到零点误差；3)进行测点规划确定测量点位，采用修正输入方式的误差补偿方法进行运动学标定，通过激光跟踪仪对标定前后的位置精度进行验证，得到的测量结果表明视觉测量方法的适用性。