新型角度检测装置及其检测方法研究*

郑伟峰

(厦门市计量检定测试院，福建 厦门 361004)

0 引 言

角度测量技术是现代测量的基础技术，随着科学技术、工业生产自动化和国防工业技术的不断发展，航空航天等大型科技探索活动对角度传感器的要求越来越高，如导弹、卫星发射过程中强冲击、强振动以及空间温度交变环境下如何实现角度的可靠性测量。角度传感器的开发紧紧围绕着高准确度、高分辨率、高可靠性、多功能、超小型和低成本而展开。研制出具有高精度、高分辨率和小型化的角度传感器解决恶劣环境和特殊要求条件下旋转运动的检测有着重大的意义[1]。

磁性角度传感器具有抗振动、抗腐蚀、抗污染的特点，尤其更容易实现高分辨率、小型化和低成本，是传统角度传感器的优秀替代品，特别适用于航天军工等环境恶劣、空间狭小的场合。迄今为止，已有一些针对此方向的研究，但是仍存在很多不足[2～4]。

本文所论述的角度位置检测方法通过简易检测元件(霍尔磁环组合)进行初始信号的采集，经过电压信号转换、模/数转换以及数字差分等一系列处理获得2组三角波原始数值。基于2组三角波原始数值的正负组合实现角度子区间的编码，并利用其中一组三角波数值实现任一子区间的角度细分，构建角度传感器分辨率与模/数转换器(analog to digital converter,ADG)分辨率的线性关系。对其中一组三角波数值经取绝对值和取反等数据处理后，结合当前两组三角波原始数值正负情况，实现子区间的识别和小分区的编号计算，实时获取当前的绝对角度输出。分析结果表明，在选用10位ADC时，该角度位置检测技术能够实现12位分辨率以上的轴角位置输出。

1 角度传感器的结构设计

对于磁性角度传感器来说，由于在信号发生部分不可避免地存在机械装配误差，使得传感器因磁环和磁敏元件外圆不同心引起信号误差；同时，磁敏元件也存在零点漂移。因此，传统的信号发生方法引入了机械误差和零点漂移，导致角度传感器信号处理计算得到的角度值存在系统误差[5,6]。

本文的信号发生部分同样也是由磁环和磁敏元件组成，磁敏元件选用霍尔元件，其工作电压为5 V。为了解决机械误差和零点漂移引入的系统误差，磁环的周围外圆上均匀分布了4个霍尔元件(A，B，C，D)，两两对称分布。本文的电路板结构布局如图1所示，机械安装如图2所示。

图1 电路板结构布局

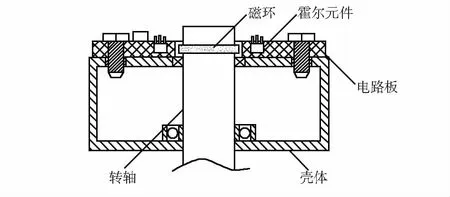
图2 机械安装结构

本文角度检测装置包括壳体和电路板，电路板固定设置在壳体一侧的外表面上，壳体内设有转轴，转轴的一端上固定套设有磁环，转轴的一端相对的另一端依次贯穿电路板和壳体且转轴与壳体转动连接，电路板上固定设有4个霍尔元件，绕磁环周围设置。4个霍尔元件分别位于同一个虚拟圆的4等分点上，且虚拟圆的圆心位于所述磁环的中心线上。运行过程中，磁环绕其旋转中心自转一周，4个霍尔元件输出一组相位各异的正弦电压信号，电压信号经过信号转换和模/数转换后，进行数字处理，最后得到磁环从初始位置旋转至预设位置的角度，能够避免信号发生部分存在机械装配误差以及传感器因磁环和霍尔元件外圆不同心引起的信号误差。通过本文设计的角度检测装置，可研制出高分辨率、高精度和适用于恶劣工况的新型磁性角度传感器，实现较高精度的绝对角度输出。

2 角度传感器的角度编码和平均细分

角度传感器运行时，磁环随着转子旋转，4个霍尔元件分别输出相位相差π/2的4路正弦电压模拟信号。电路板上分别设计了4路独立的正弦波—方波—三角波电压转换电路。转换电路分别将4路正弦电压信号成功转换成4路三角波电压信号。以霍尔元件A和B的电压模拟信号为例，其转换后的三角波电压模拟信号如图3所示。转子旋转1周，可得到1个周期(0～2 π)的A和B三角波电压模拟信号，其相位差180°。

相位差180°的三角波电压经模/数转换后，当采用的ADC分辨率为n时，得到数值波形如图3(b)所示。

图3 A和B的电压模拟信号和电压模/数转换后的数值

处理芯片对其进行数字差分处理(A电压信号的模/数转换结果a与B电压信号的模/数转换结果b相减)，获得有正负的原始三角波数值(a-b) 。同样的，经过处理后亦可获得有正负的原始三角波数值 (c-d)。当采用分辨率为n的ADC芯片，转子旋转1周，(a-b)和(c-d)一个周期的原始数值变化如图4所示。

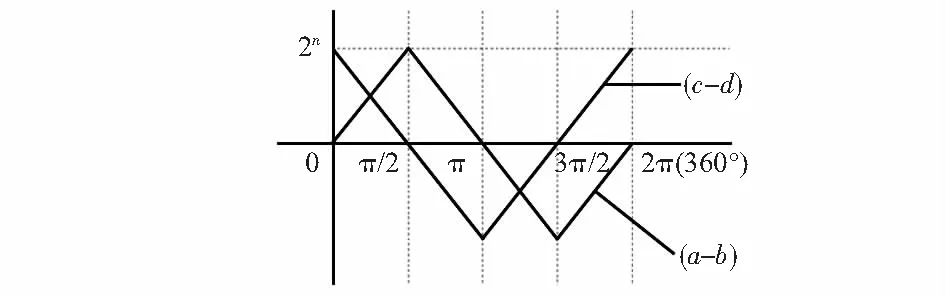
图4 (a-b)和(c-d)一个周期的原始数值变化

转子旋转1周，处理芯片经过数字差分后得到1个周期的原始三角波数值(a-b)和(c-d)。(a-b)和(c-d)数值波形相位差90°，均有正负值。(a-b)和(c-d)联合提供正负信息，可用于子区间的编码。根据(a-b)和(c-d)的正负组合，将(0°～360°)平均分为4个子区间，并进行编码。编码结果如图5所示。第一角度区间范围(0°～90°)，编码为“11”的子区间(即(a-b)>0，(c-d)>0)；第二角度区间范围(90°～180°)，编码为“10”的子区间(即(a-b)>0，(c-d)<0)；第三角度区间范围(180°～270°)，编码为“00”的子区间(即(a-b)<0，(c-d)<0)；第四角度区间范围(270°～360°)，编码为“01”的子区间(即(a-b)<0，(c-d)>0)。

图5 四个子区间的编码

实现了子区间的编码后，处理芯片对图5中的三角波原始数值(a-b)取绝对值处理。因此，转子旋转1周，1个周期内的|(a-b)|数值变化如图6所示。

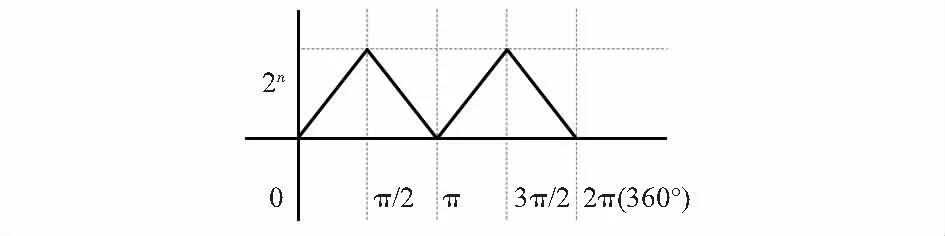
图6 1个周期内的|(a-b)|数值变化

从图6可以看出，模/数转换芯片的有效位数为n，因此 |(a-b)|的数值变化范围为(0～2n)。将1周的(0°～360°)平均分成四个子区间，每个子区间又可以平均细分成2n个小分区。因此，(0°～360°)可平均细分为4×2n个小分区。每个小分区代表一个角度值大小。当转子旋转到某一个位置时，通过当前电压采集和信号处理后，只要计算出对应的小分区序号，就能准确计算出当前的旋转角度。

3 角度传感器的信号处理和角度计算

在上文中，尽管成功地将(0°～360°)细分成4×2n个小分区，但是当转子处于某一位置时，还是无法利用采集到当前电压信号及后续数字处理结果计算出小分区的序号。转子在同一方向旋转过程中，处理芯片获得的|(a-b)|数值在4个等分子区间内并非统一的递增或者递减变化，这就导致各个小分区的序号存在跳跃的现象，各个小分区序号很难与|(a-b)|的数值建立连续一一对应关系。因此，本文对一个周期(0°～360°)范围内的|(a-b)|数值进行了处理。将编号为“10”和“01”的子区间的|(a-b)|数值进行取反处理。当原始数值(a-b)和(c-d)处于编号为“10”和“01”的子区间时，令F(|(a-b)|)=2n-|(a-b)|，当原始数值(a-b)和(c-d)处于编号为“11”和“10”的子区间时，令F(|(a-b)|)=|(a-b)|。处理完的F(|(a-b)|)数值变化如图7所示。转子在同一方向旋转过程中，处理完的数值F(|(a-b)|)在4个子区间实现了统一的递增或者递减变化。

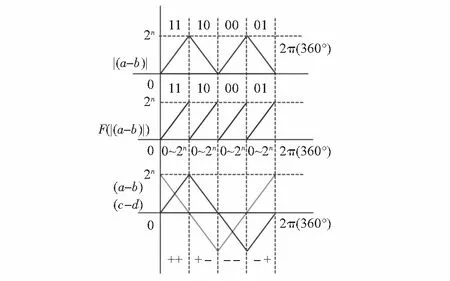
图7 处理完F(|(a-b)|)的数值变化

处理芯片每间隔60 μs完成一次当前的霍尔电压信号采集和数据处理，并实时计算当前对应的角度值。当转轴旋转时，处理芯片首先根据原始数值(a-b)和(c-d)判断当前所在子区间，然后读取F(|(a-b)|)值，计算小分区的序号值，进而计算出转子的角度值。通过与修正值的叠加计算，可获得高精度的角度。假设当前转子旋转到(180°～270°)的子区间。处理芯片采集和处理得到(a-b)和(c-d)的正负值分别“-”和“-”，那么当前应该是处于编号为“00”子区间。读取F(|(a-b)|)的值，即可判断当前对应的小分区序号应该是F(|(a-b)|)。利用小分区编号和子区间编码即可计算出当前角度值。

如果磁环的初始位置位于第一角度区间的某个位置，预设位置在第三角度区间的某个位置，则处理芯片采集和处理得到(a-b)和(c-d) 的正负值应该分别“+”和“+”，(a′-b′)和(c′-d′)的正负值应该分别“-”和“-”，那么对应的编码区间应该分别为“11”和“00”，获取F(|(a-b)|)和F(|(a′-b′)|)的值，即可判断当前对应的小分区序号应该分别为是F(|(a-b)|)和F(|(a′-b′)|)，将F(|(a-b)|)和F(|(a′-b′)|)分别代入角度计算函数中，得到两个在角度区间中的角度(假设一个为30°，另一个为25°)，最后可计算出第一旋转角度为30°(即磁环的初始位置位于30°位置)，第二旋转角度为25°+180°=205°(因为通过判断位于第三角度区间的某个位置，应加上180°)，由此可计算出最终的磁环从初始位置旋转至预设位置的旋转角度：205°-30°=175°。以下的步骤1～步骤8是本文新型角度检测装置的工作流程：

步骤1 将磁环绕其旋转中心自转一周的角度划分成4个依次连续的等角度区间；

步骤2 当磁环位于初始位置时，采集4个霍尔元件的第一电压值；

步骤3 将采集到的4个霍尔元件中相位相差180°的2个霍尔元件中的相位在前的霍尔元件的第一电压值减去相位滞后的霍尔元件的第一电压值，得到两个电压差值；

步骤4 根据所述两个电压差值的正负情况，分析出磁环当前所在的角度区间；

步骤5 对两个电压差值中的一个电压差值取绝对值，得到电压绝对值；

步骤6 根据所述电压绝对值以及分析出的磁环当前所在的角度区间，计算得到磁环的第一角度；

步骤7 将磁环旋转至预设位置时，采集4个霍尔元件的第二电压值，将所述第二电压值作为第一电压值，返回步骤3并执行步骤3—步骤6，计算得到磁环的第二角度；

步骤8 将计算得到的所述第二角度减去所述第一角度，得到磁环从初始位置旋转至预设位置的旋转角度。

4 结束语

本文提出了一种新型角度传感器的绝对编码细分算法，消除机械装配偏差和霍尔元件的零点漂移带来的信号误差。研究了1个旋转周期内子区间的编码和细分方案，利用两组三角波原始数值当前的正负组合实现了子分区的编码和识别，利用其中一组三角波数值取绝对值和取反处理后的当前结果进行小分区序号的计算。最后，通过小分区序号和子区间编码与角度值建立对应关系，实现了转子角度绝对位置的实时检测。分析结果表明：当ADC分辨率为10位时，该算法可以实现12位分辨率的轴角位置检测，通过提高ADC分辨率后，可以进一步提高该角度传感器的分辨率和精度。