论出射光线与入射光线平行的充要条件——对2020年7月浙江省物理高考第13题的严格论证

闫二斌 景银安 杨 洋 王伟民 郝晨凯

（1.宜川县中学，陕西 延安 716200；2.太和县宫集镇中心学校，安徽 卓阳 236652；3.阿房路三校，陕西 西安 710016）

例题.（单选）如图1所示，圆心为O、半径为R的半圆形玻璃砖置于水平桌面上，光线从P点垂直界面入射后，恰好在玻璃砖的圆形表面发生全反射；当入射角θ=60°时，光线从玻璃砖圆形表面出射后恰好与入射光线平行.已知真空中的光速为c，则

图1

1 试题剖析

此题考查全反射、折射定律、平行玻璃砖、折射率、光在介质中的传播速度、临界角等知识，以及数学能力和综合运用知识的能力，难度较大.

解答此题时，首先不难画出垂直入射时的光路图，如图2所示.设玻璃砖的折射率为n，在圆形界面恰好发生全反射时的入射角为C，则根据折射定律有

图2

而入射角θ=60°时的光路图不好画，因为难以找到光在玻璃砖中的出射点.这也是此题最难突破的地方.但是如果根据已知“出射光线与入射光线平行”并且想到“光入射平行玻璃砖时，出射光线与入射光线平行”，再加上圆的简单几何性质，则容易判断出此时的出射点就是半圆玻璃砖的顶点，因为半圆顶点处的切线与OP平行，相当于“平行玻璃砖”.此时的光路图如图3所示.设在P点折射时的折射角为θ2，则易知在顶点折射时的入射角也为θ2，则有

图3

回看上述解答过程，部分心细的学生可能会在好奇心的驱使下心存疑虑：如果第2次光不是从玻璃砖的顶点射出，则出射光线有没有可能也会平行于入射光线？如何来论证这个问题？此时有两种情况，出射点偏左如图4所示和出射点偏右如图5所示.对于图4中的情形，根据圆周角和三角形外角的知识（如图6所示），易知θ3＜θ2，则此时出射光会更加靠近法线，但是相比于从顶点出射，法线向左偏转了，所以不能排除出射光与入射光平行的情况.同理，对于图5中的情形，也不能排除出射光与入射光平行的情况.这些困难是由于光进入玻璃砖第二次折射时的入射角、法线、折射角都在变化，而且圆中的几何比较复杂造成的.如果能够从中提炼出“光射入非平行玻璃砖时，出射光线与入射光线一定不平行”或者说“当且仅当，光射入平行玻璃砖时，出射光线才平行于入射光线”的论断，然后再证明这个论断，问题就会变得明朗起来.

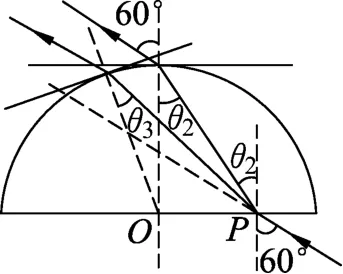
图4

图5

图6

图7

2 充要性论证

根据上面的分析，我们已经将问题的焦点转移到寻求出射光线与入射光线平行的充要条件上来.易知，若光入射平行玻璃砖，则一定有出射光线与入射光线平行（证明略），如图8所示.而若光入射某玻璃砖，发现出射光线与入射光线平行，则这个玻璃砖一定是平行玻璃砖吗？答案是肯定的，证明如下.

图8

方法1.采用反证法.如图9，光入射某玻璃砖（界面不平行），且出射光线与入射光线平行，设玻璃砖的折射率为n，第一次折射时的入射角为θ1，折射角为θ2，第2次折射时的入射角为θ3，折射角为θ4，则根据折射定律，有

图9

再过第2次折射点，做第1次折射时的法线的平行线，设第1次折射时的法线与第2次折射时的法线的夹角为α，如图10所示.则根据平行关系，易知

图10

将（5）式代入（4）式，有

图11

方法2.如图12所示，设光线第一次折射时顺时针偏转α1，第2次折射时逆时针偏转α2，则易知出射光线平行于入射光线的充要条件是α1=α2.做出法线，设此时出射光线平行于入射光线，α1=α2=α，且设出各角如图13所示.则由折射定律可得

图12

图13

应用两角和公式对（7）式进行化简，可得tanθ1=tanθ2，即θ1=θ2，而这便意味着两次折射的法线平行，即为平行玻璃砖.即命题得证.

方法3.想象实验法.如图14，光射入平行玻璃砖，出射光线与入射光线平行，现在假设通过一种实验操作将玻璃砖的上界面改变到图14中虚线的位置，则易知出射光线的方向一定会改变，因为发生第2次折射前的光路没有任何变化，玻璃的折射率没有变，而玻璃砖的上界面发生了变化，所以出射光线的方向一定会发生变化，而之前其与入射光线平行，变化之后则一定不平行，所以不平行玻璃砖的出射光线与入射光线一定不平行，命题得证.

图14

综上所述，根据所证明的“光入射玻璃砖时，当且仅当出射界面与入射界面平行时，出射光线才平行于入射光线”，不难得知光线必须从圆形玻璃砖的顶点出射，才能满足题意.