一道高考试题背后的高等数学背景

甘肃省兰州市第二十七中学 陈鸿斌730030

纵观近几年的高考,以初等函数为背景来命制压轴题是个趋势,有时还会渗透高等数学背景.随着高考命题改革的逐步深入,为了渗透新课程理念,命题者常受到自身学术和研究方向的影响,往往考查一些有着高等数学背景的问题.此类题目设计形式新颖,成为高考试卷中一道亮丽的风景线.因为这些问题以高等数学知识为背景,即试题的设计来源于高等数学,但解决的方法却是高中数学所学的初等数学知识,对学生思维的逻辑性、抽象性以及学生的理解能力和自学能力提出了更高的要求,着力考查数学核心素养.

1 题目呈现

本题是2020年高考数学文科试题全国卷II的第21题.本文就来揭示本题背后的高等数学背景——Lagrange中值定理.

2 高等数学背景解读

本题的第（2）问就具有《数学分析》[1]中“Lagrange中值定理”的背景.

几何意义:曲线在x=ξ处的切线与(a,f(a))和(b,f(b))的连线平行,或者说,曲线在x=ξ处的切线斜率与(a,f(a))和(b,f(b))的连线的斜率相等.如图1所示.

图1

3问题解答

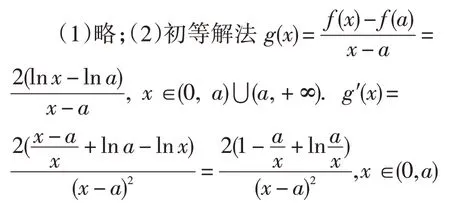
点评：本题主要考查函数的单调性、最值、导数、含参不等式恒成立等基本知识，考查数形结合、化归与转化等数学思想方法和分析问题、解决问题的能力.作为一线的中学教师，看到本题的表达形式，要能够领悟命题者的设计意图，背景来源于Lagrange中值定理.因此本题体现了高等数学与高中数学教学之间较好的衔接，很好地考查了学生的学习潜能，有利于高校选拔人才.从笔者给出的初等解法和高等解法可以看出，运用Lagrange中值定理求解第（2）问，比高考参考答案的解答简便了许多.换个角度,看的会更加透彻.

4 追溯姊妹题

t ( )0,32( )3 ,+∞2 3 0 2 u′(t)u()t_↘极小值334+↗

即证∀x＞0,x3-4x+4＞0.设u(x)=x3-4x+4(x＞0),则u′(x)=3x2-4,列表：

x■■■0,2 3■ ■■23 0■ ■■23,+∞■■■u′(x)u(x)_↘+↗36-163 9

例2（2006全国Ⅱ,理20）设函数f(x)=(x+1)ln(x+1).若对所有的x≥0,都有f(x)≥ax成立,求实数a的取值范围.

初等解法 令g(x)=(x+1)ln(x+1)-ax,于是不等式f(x)≥ax成立，即为g(x)≥0成立.对函数g(x)求导数:g′(x)=ln(x+1)+1-a.令g′(x)=0,解得x=ea-1-1.（1）当x＞ea-1-1时,g′(x)＞0,即g(x)在(ea-1-1,+∞)单调递增；（2）当-1＜x＜ea-1-1时,g′(x)＜0,即g(x)在(-1,ea-1-1)单调递减.所以要对所有x≥0,都 有g(x)≥0 的 充 要 条 件 为ea-1-1≤0.由此得a≤1,即a的取值范围是(-∞,1].

由此可见,上述姊妹题都渗透了Lagrange中值定理的高等数学背景,用Lagrange中值定理求解降低了运算量,优化了解题思路,正所谓:站得高才能看得远.

5结束语

以高等数学为背景的高考试题通常以高等数学概念、公式、定理、性质等为命题背景,或体现高等数学中常用的思想方法及推理方法等.以高等数学为背景命题是命题者居高临下设计试题的方式,能从更高层次考查学生的思维能力,核心素养.虽然命题者根据高等数学的内容来设计这些试题，只是创设了一种情境,并不要求学生用高等数学的知识去解决问题,解决的方法还是初等方法,体现了数学学科的整体性和数学教育的连续性,显示了高等数学对初等数学的指导作用.作为一名高中数学教师要用新课程标准和高考审视常规教学,随时对自己的教学进行研究、反思,使自己的知识结构具有前瞻性,这样才能正确把握高考的新动向,以及命题趋势,发展学生数学学科的核心素养.