基于轮轨动力响应的地铁波磨地段钢轨打磨限值研究

江万红 王显 韦凯 王平

1.中铁二院工程集团有限责任公司，成都 610051；2.西南交通大学高速铁路线路工程教育部重点实验室，成都 610031

随着城市轨道交通飞速发展，轨道系统病害日益引起关注。钢轨波磨是指在轮轨滚动接触表面出现的类似波浪的规律性不均匀磨耗现象，产生机理复杂，治理困难，已经成为困扰我国城市轨道交通发展的主要问题之一［1］。我国各地地铁线路的直线与小曲线半径地段中均出现了不同程度的波磨现象，波长在30~100 mm［2-3］。该范围内的波磨会引起轮轨结构的强烈振动并产生强烈的轮轨滚动噪声，会导致轨道系统各部件疲劳损伤，危害列车行车安全性，影响旅客乘坐舒适性。

目前对于钢轨波磨的产生原因尚无统一的认识，一般分为动力类成因与非动力成因理论［4］。动力类成因理论认为，钢轨波磨是由于轮轨间的固有属性或轨道间的初始不平顺在振动作用下引起的自激振动或共振现象［5-6］；非动力成因理论认为，钢轨波磨主要是由于钢轨自身残余应力或轮轨间接触疲劳产生的［7-8］。

为保证线路的运行安全，对波磨的治理刻不容缓。可采用摩擦吸振器［9-10］、轨道吸振器［11-12］等设备来调节轮轨间的摩擦属性或振动特征，起到减轻轮轨振动、抑制波磨的效果。在实际线路中，产生波磨时，一般首先通过降低运营时速或钢轨打磨的方法来抑制波磨状态下的轮轨动力响应［13-14］。

由于地铁复杂线形条件下钢轨波磨对不同车速轮轨动力响应的影响尚不明确，无法确保降速后的轮轨动力响应满足相关规范要求。目前地铁钢轨打磨主要依据TG∕GW 102—2019《普速铁路线路修理规则》，但地铁线路小曲线半径地段较多，行车密度大，列车加减速频繁，轨道磨耗特点与普速铁路有所不同。因此，为确保线路的安全，应根据线路实际情况确定限速条件与钢轨打磨标准。

本文在一地铁线路上选取一段小半径曲线地段，通过多刚体动力学软件UM建立曲线段车辆-轨道耦合动力学模型，通过分析不同车速与不同波磨状态下的轮轨动力响应，研究曲线波磨地段的整治措施及其整治效果。

1 车辆-轨道耦合动力学模型

1.1 车辆模型

车辆采用地铁A型车。车体、转向架、轮对质量分别为24.0、3.2、2.5 t；轮对廓形为LM。一系、二系弹簧垂向刚度分别为10.00、0.25 kN∕m，垂向阻尼分别为6、20 kN·s∕m。车速为120 km∕h。

运用多刚体动力学软件UM建立具有35个自由度的车辆模型，如图1所示。

图1 车辆模型

1.2 轨道模型

钢轨为CN60钢轨，轨间距1 435 mm，设1∕40轨底坡。扣件垂向、横向刚度分别为30、23 MN∕m，垂向阻尼34.8 kN·s∕m；扣件间距595 mm。

根据地铁线路的实际状态，轨道线形为直线段—缓和曲线段—右侧圆曲线段—缓和曲线段—直线段，长度依次为70、115、450、115、50 m。曲线半径为800 m，实设超高150 mm，列车以120 km∕h驶过时，欠超高达60 mm，故圆曲线段具有较大的、未被平衡的离心加速度。根据实测数据，地铁线路的钢轨波磨主要发生在圆曲线及缓和曲线段内，并从圆曲线到缓和曲线呈逐渐减缓的趋势。因此，分析时提取最不利的圆曲线段的计算结果即可满足要求。

1.3 轨道不平顺

根据现场实测的波磨状态，采用波长为40 mm、波深为0.11 mm的典型谐波不平顺作为波磨条件下的不平顺输入，如图2所示。考虑线路正常运行时的轮轨动力响应时，采用美国五级谱作为线路的不平顺激励输入，如图3所示。

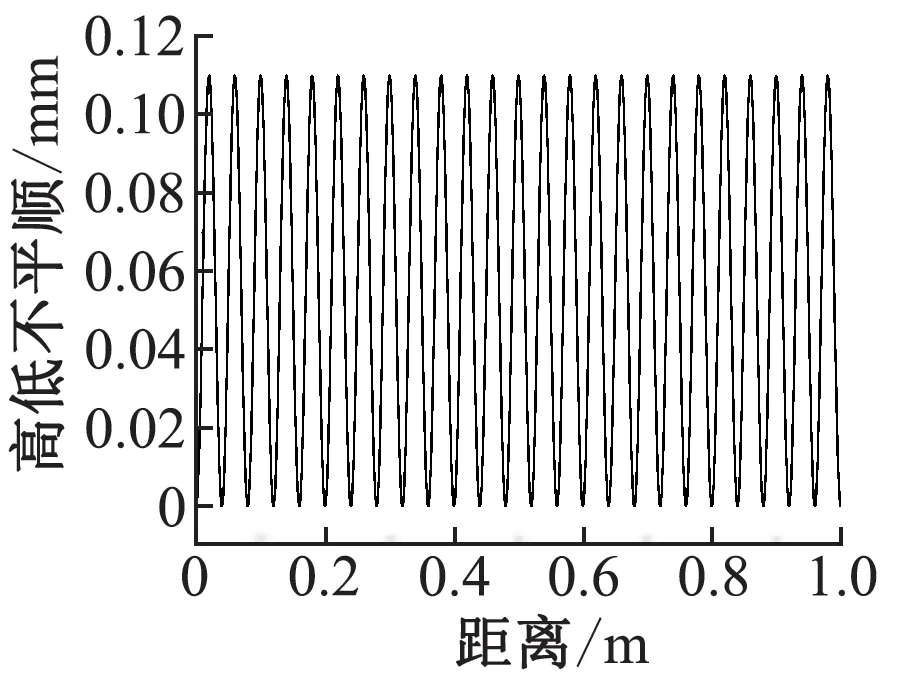
图2 短波波磨

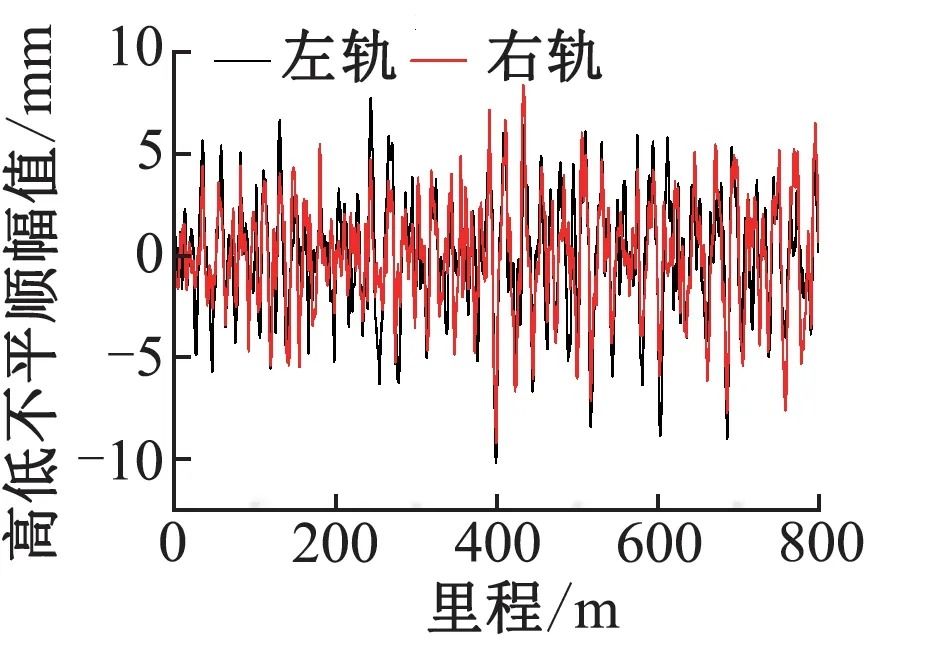
图3 美国五级谱

1.4 计算原理

在UM软件中，首先生成整个系统的动力学方程与计算初始条件，再通过Park Pallel法求解系统每一步系统的各个结构的动力响应［15］。

根据动力学基本原理，进行动力学计算时，系统的动力学方程表示为［16］

式中：M、C、K分别为系统的质量矩阵、阻尼矩阵、刚度矩阵；a、v、x分别为系统的加速度、速度和位移；F为外部输入荷载。

1.5 模型验证

为了验证所建车辆-轨道耦合动力学模型的正确性，采用文献［17］的实测数据，仿真计算波磨条件下钢轨垂向振动加速度，并与实测结果对比，见图4。可知，钢轨垂向振动加速度的实测结果、仿真结果最大值分别为2 171.01、2 075.51 m∕s2，仅相差4.6%，且波形吻合程度较好。因此，本文所建车辆-轨道耦合动力学模型可靠。

图4 钢轨垂向振动加速度仿真与实测结果对比

2 波磨对车辆-轨道耦合系统的影响

分析曲线地段波磨出现前后轮轨动力响应变化，研究短波波磨激励对车辆、轨道系统的影响。

2.1 轮轨荷载响应

以左侧导向轮为例，计算其轮轨垂向力、横向力及轮重减载率、脱轨系数，结果见图5。可知：五级谱工况下的圆曲线段轮轨垂向力最大值为74.46 kN，对应的波磨工况下为116.93 kN，增长57.04%；五级谱工况下的轮轨横向力最大值为5.54 kN，对应的波磨工况下为27.15 kN，增长397.10%；五级谱工况下的左侧导向轮轮重减载率最大值为0.72，而对应的波磨工况下已达1.00，轮轨间已脱离接触；五级谱工况下的左侧导向轮脱轨系数最大值为0.14，对应的波磨条件下已达0.31，增长121.3%，车辆脱轨风险增大。可见，波磨的存在会加剧轮轨间的动力响应，降低车辆运行的安全性与平稳性。

图5 左侧导向轮的轮轨动力响应

2.2 轨道系统动力响应

计算圆曲线段钢轨振动加速度、垂向位移，结果见图6。可知：五级谱工况下的钢轨振动加速度最大值为88.72 m∕s2，对应的波磨工况下为2 075.51 m∕s2，增长了约22倍；五级谱工况下的钢轨位移最大值为0.77 mm，对应的波磨工况下为0.68 mm，减小约11.69%。可见，钢轨波磨的存在将导致轨道系统加速度响应激增，但对钢轨位移影响不大。

图6 曲线段钢轨系统动力响应

综上，钢轨波磨的存在会导致轮轨相互作用加剧，增大列车运行过程中的脱轨风险；同时使轨道系统的振动加速度激增，在共振状态下易引起轨道系统零部件的伤损。

3 波磨条件下地铁降速标准及打磨标准

利用所建车辆-轨道耦合动力学模型，分析在不同车速与不同波磨状态下曲线段轮轨系统响应变化规律，研究车速与波磨状态对轮轨系统动力响应的影响。

3.1 设计指标限值

参照GB∕T 5599—2019《机车车辆动力学性能评定及试验鉴定规范》的相关要求，轮轨横向力Q的限值条件为Q≤0.4P0，P0为静轴重；轮轨垂向力P的限值条件为P≤90+Pst，Pst为静轮重。代入计算参数后，算得模型中的轮轨横向、垂向力限值分别为38.4、138.0 kN。脱轨系数限值为1.0；轮重减载率限值为0.6。

参照TB 10761—2013《高速铁路工程动态验收技术规范》中的相关要求，钢轨垂向振动加速度限值为5 000 m∕s2，钢轨位移限值为2.0 mm。

3.2 车速影响分析

为明确波磨条件下的安全车速，计算车速为60、80、100、140、160 km∕h时曲线波磨地段的轮轨动力响应，结果见图7。可知：

1）波磨条件下轮轨动力学响应与车速正相关，车速越高，轮轨间各项动力响应越大。

2）车速从60 km∕h提升至160 km∕h，车辆垂向轮轨力最大值从79.6 kN提升至181.2 kN，增大了127.5%，车速140 km∕h时已超过限值；车辆轮重减载率最大值从0.48提升至1.00，增大了108.1%，车速80 km∕h时已超出限值；轮轨横向力、钢轨位移、钢轨振动加速度、车辆脱轨系数最大值分别增大了508.1%、64.8%、358.5%、314.3%，均未超出限值。

综上，对于发生短波波磨的地铁线路，列车运营速度低于80 km∕h时，系统各项动力指标处于安全范围内。因此，建议对于已发生短波波磨地段，列车运营速度降低至80 km∕h以下。

图7 不同车速下曲线段系统动力响应

3.3 波磨状态影响分析

取波长为20、40、80、160、320 mm，波深为0.05、0.10、0.20、0.30、0.40、0.50 mm，计算不同波长与波深条件下，轮轨系统各部分动力响应，计算结果见图8。可知：

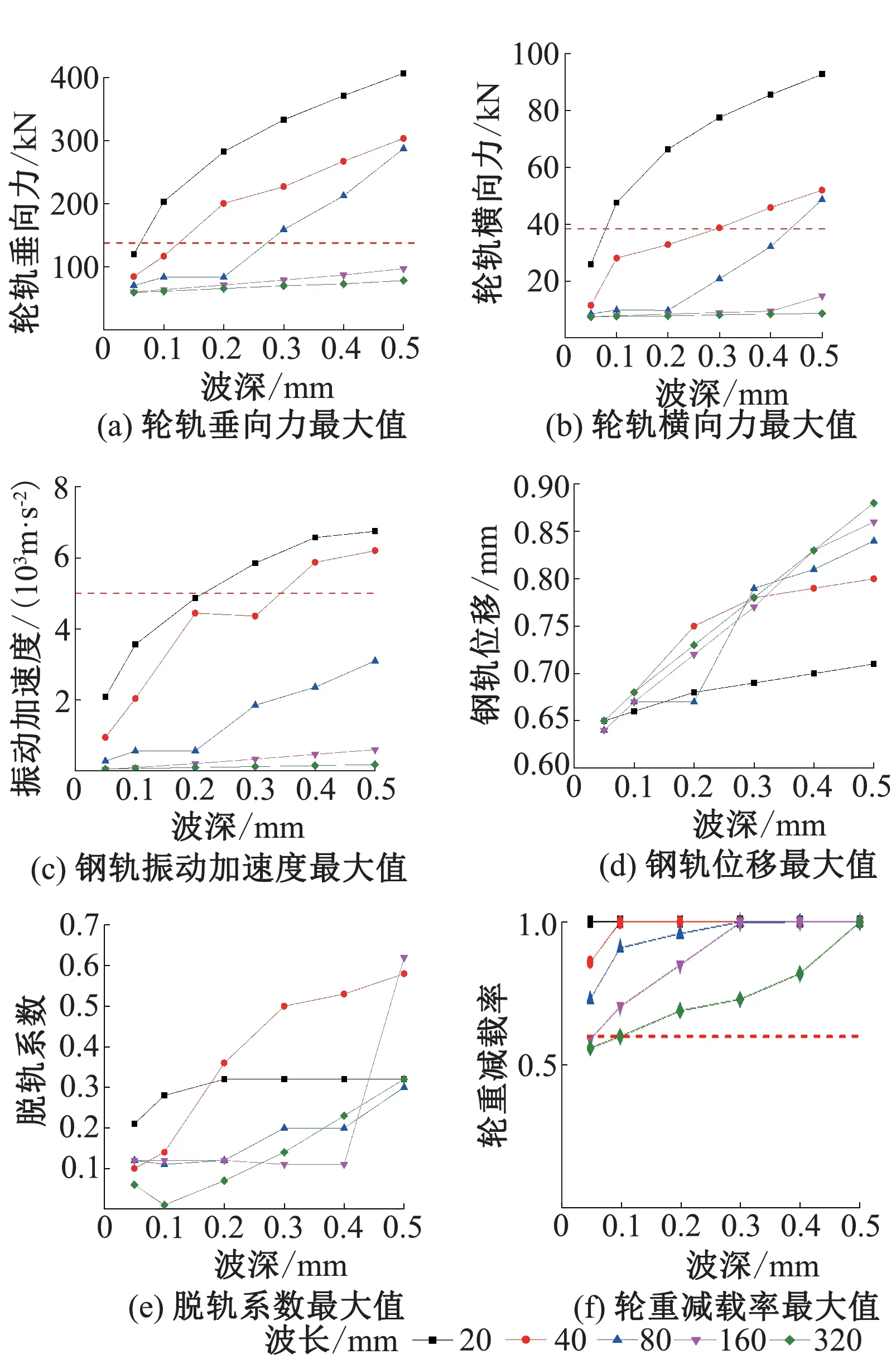
图8 不同波磨状态下曲线段耦合系统动力响应

1）在相同波长条件下，轮轨系统各项动力响应随着波深的增长而不断增大，同时波长越短，轮轨系统响应受波深的影响越大。例如，波深从0.05 mm增至0.50 mm时，波长为40 mm条件下，轮轨垂向力最大值从84.7 kN增至303.6 kN，增大了258.5%；轮轨横向力最大值从11.4 kN增至51.9 kN，增大了355.3%；而波长为320 mm条件下，轮轨垂向、横向力最大值分别增大了31.7%、17.7%。

2）在相同波深条件下，轮轨系统各项动力指标随波长的增长而降低，且波深越大，动力响应变化越剧烈。例如，波长从20 mm增至320 mm时，钢轨振动加速度最大值在波深0.10 mm条件下减小3 491.9 m∕s2，而在波深0.50 mm条件下减小6 569.6 m∕s2。

3）除钢轨位移、脱轨系数在不同工况下均未超出规范限值外，其他指标均存在一定的超限情况，且波长越短，超限情况越严重。另外，各指标对波磨敏感程度不同。例如，波长为80 mm时，各波深条件下的轮重减载率均已超限，轮轨垂向力超限波深为0.20 mm，轮轨横向力超限波深为0.40 mm，钢轨振动加速度未超出规范限值。

3.4 钢轨打磨标准研究

为保证波磨地段车辆运行的安全，须确定不同波长下的钢轨打磨标准。

轮重减载率对波磨极为敏感，当波长较小时，较低的波深就会导致轮重减载率超出规范限值。取波深为0.02、0.05、0.10 mm，计算波长分别为20、40、80、160 mm时车辆-轨道耦合系统的轮重减载率，结果见图9。可知：波长20~80 mm时，只有波深小于0.02 mm条件下轮重减载率才满足规范限值；波长为160 mm时，其超限波深为0.05 mm。

图9 不同波长下的轮重减载率

以对波磨敏感程度最高的轮重减载率与轮轨力为钢轨打磨标准的主要限值指标，确定各波长范围内的钢轨波磨打磨限值，见表1。可知，车辆-轨道耦合系统各项动力响应对短波长的波磨更为敏感，因此短波条件下的波磨打磨限值较为严格；波长较大时，耦合系统各项动力指标未超出规范限值，其打磨限值较短波情况下更宽松。

表1 各波长条件下的钢轨打磨标准

4 结论及建议

1）钢轨波磨会导致轮轨系统的动力响应急剧增大，增大列车运行过程中的脱轨风险，同时使轨道系统的振动加速度激增，在共振状态下易引起轨道系统零部件的伤损，严重影响车辆运行的安全性与平稳性，但对钢轨位移影响较小。

2）波磨条件下轮轨动力学响应与车速正相关，车速越高，轮轨间各项动力响应越大。车速小于80 km∕h时，耦合模型各项动力指标均处于安全范围内。因此针对出现短波波磨的区域，可首先通过降速至80 km∕h以下来保证线路运营安全。

3）在相同波长条件下，轮轨系统各项动力响应随着波深的增长而不断增大，同时波长越短，轮轨系统响应受波深的影响越大。

4）在相同波深条件下，轮轨系统各项动力指标随波长的增长而降低，且波深越大，动力响应变化越剧烈。

5）各指标对波磨敏感程度不同，轮重减载率与轮轨力对波磨敏感程度最高的。

6）以轮重减载率与轮轨力为主要依据，提出了钢轨波磨波深打磨标准。建议波长为20~80、80~160、160~320 mm时的钢轨打磨限值分别为0.02、0.05、0.10 mm。