提升初中生直观想象素养的教学策略研究*——以图形的变化教学为例

广东省广州市白云区三元里中学(510400) 肖 乐

1 问题提出

直观想象是《普通高中数学课程标准(2017 版)》中提出的6 大数学核心素养之一,是发现和提出问题、分析和解决问题的重要手段,是探索和形成论证思路、进行数学推理、构建抽象结构的思维基础[1],对学生数学学习、思维发展有重大意义.在初中阶段,与之对应的是几何直观与空间观念这两个核心词.图形的变化是初中图形与几何的核心内容,包含5 种图形的变换与运动,是对图形的一种动态研究,学生对其的掌握水平,能直接反映直观想象素养水平.义务教育学段数学课程标准(2011 版)出台后,平移、轴对称、旋转等图形的变化逐渐成为中考压轴题的常见素材,对学生的思维发展提出了较高要求.因此,学生掌握好这一内容,对提高数学成绩,培养分析和解决问题的能力,发展思维水平,提升直观想象素养尤为重要.但由于初中生普遍思维发展水平不高,文字阅读理解和数学语言表达能力不足,图形的变化因此成为教与学中的难点,该如何解决这个问题呢? 本文以轴对称和旋转变换为例,探究在初中数学课堂中如何运用教学策略提升学生直观想象素养.

2 概念界定和研究意义

直观想象是指借助几何直观和空间想象感知事物的形态与变化,利用空间形式特别是图形,理解和解决数学问题的素养.主要表现为: 建立形与数的联系,利用几何图形描述问题,借助几何直观理解问题,运用空间想象认识事物[2].在初中阶段,与之对应的是几何直观与空间观念.

图形的变化是指图形的变换和运动, 包含图形的轴对称、图形的旋转、图形的平移、图形的相似、图形的投影等5个内容,是对图形的一种动态描述和研究.

研究意义:

2.1 直观想象不但包含了数形结合,还包含了空间位置关系、形态变化与运动规律.而图形的变化是学生在学习了对图形的静态描述——基本图形的概念和性质后,从运动的观点和变化的角度来研究图形[3],即对图形进行动态解释,这是一种更高阶的思维方式.对图形的这一研究过程可以促进学生体会直观与逻辑、直觉与证明之间的关系,是培养学生几何直观、空间观念的一种重要方法;

2.2 由于图形的变化这一内容的丰富性和趣味性,不但有助于学生感受数学的直观美,提高学习兴趣,其所蕴含的数形结合、转化与化归、分类讨论、建模等基本数学思想,拓宽了初中课程的视野,促进学生向高阶思维发展,促进直观想象等数学素养的提升.最终实现让学生学会用数学的眼光发现世界,数学的思维思考世界,用数学的语言表达世界的理想境界.

3 有效提升直观想象素养的教学策略

3.1 体验数学活动,感受变化魅力,提升直观想象素养

活动1 如图1 所示, 将一张正方形纸片先由下向上对折, 再由右翻起向左对折, 得到图③的正方形AOBC.把图③剪掉阴影部分等腰直角ΔMON后, 得到图④五边形AMNBC.将图④纸片展开铺平后,请问是下面A、B、C中哪个图形? 为什么?

图1

此问题考查轴对称图形的性质,解答关键在于把图形沿对称轴进行展开或还原,学生在脑海中呈现这一过程时,空间观念能力得到发展.过程如下: 把第④幅图沿对称轴BN所在的直线向右对折,打开得到.再沿对称轴AM所在的直线向下对折打开,所以得到.教师进一步提出问题: 如果已知和等被剪好的图形,你能用剪刀和纸片还原剪裁的过程中吗?

活动2 如图2,由4 个全等的正方形组成的L形图案,请按下列要求画图:

图2

(1)在图案①中添加1 个正方形,使它成轴对称图形但不能是中心对称图形;

(2)在图案②中添加1 个正方形,使它成中心对称图形但不能是轴对称图形;

(3)在图案③中改变1 个正方形的位置,从而得到一个新图形,使它既是中心对称图形,又是轴对称图形.

大家互相交流一下想法,看看哪个小组的办法最多?

本活动综合考查了中心对称图形及轴对称图形的性质,以及作图方法,找对称轴及对称中心是解决问题的关键.经过学生的认真思考和热烈讨论,分别得到第(1)问的3 个答案,如图3 所示;第(2)题答案,如图4 所示;第(3)问的2 个答案,如图5 所示.

图3

图4

图5

活动3 我是设计师活动: 请你用学过的轴对称、旋转等图形的变化,设计出美丽的图案吧.图6 为笔者学生的作品.

图6

这些数学活动给课堂增加了艺术性和趣味性,学生在观察、思考、操作的过程中,既能直观感受图形的对称美,又加深了对其性质的认识理解, 几何直观与空间观念得到发展,直观想象素养得到提升.

3.2 依托基本图形,迁移拓展补充,提升直观想象素养

3.2.1 利用图形的轴对称变换,解决线段之和最短问题

案例1将军带着马从营地点A出发,先前往河边l某处点P饮水,然后再前往点B处吃草,请问饮水点P在河边哪个位置,将军和马所走的路程之和最短.如图7,我们称之为“将军饮马”基本图形,即要求线段PA+PB之和最短.

图7

这是人教版八年级的经典问题, 解决方法为以河边l为对称轴,做点A关于直线l的对称点A′,连接BA′.线段PA+PB之和被转化为线段BA′的长度,根据两点之间线段最短,当B、P、A′三点共线时PA+PB之和最短,此时线段BA′与直线l的交点P为所求.我们可以对这个基本图形进行迁移、拓展和补充.

片段1 如图8,正方形ABCD的边长为8,N在DC上,且DN=2,M是AC上一动点,求DM+MN的最小值.

图8

解析: 如图9,类比基本图形,可以把AC看做“河边l”,D和N分别看做上题中的营地A和草地B,点M看做饮水点P.由于正方形本身具有对称性,对角线所在的直线为对称轴,因此点B就是点D的对称点,则DM+MN的最小值可以转化求BM+MN最小值,再根据两点之间线段最短,问题最终转化为求线段BN的长.此问题中,把求折线和转化为求线段长度,这一过程可称之为“化折为直”.

图9

片段2 如图10,点A是半圆上(半径为1)的三等分点,B是劣弧AN的中点,P是直径MN上一动点,求PA+PB的最小值.

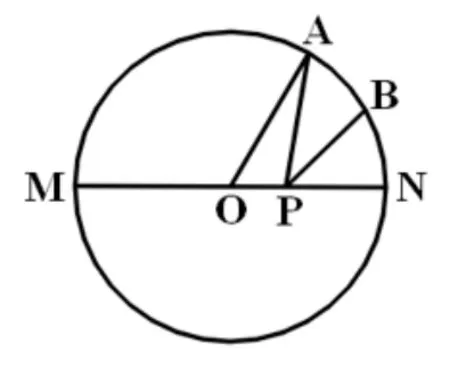
图10

解析: 此题把具有对称性的圆做为载体,则直径所在的直线为对称轴.如图11, 根据垂径定理找到点B的对称点B′,则PA+PB的最小值问题转化为求PA+PB′的最小值,即求线段AB′的长,同样也是“化折为直”.

图11

片段3 如图12, 在锐角ΔABC中,AB=∠BAC= 45°, ∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,求BM+MN的最小值.

图12

解析: 此问题背景虽然是没有对称性的一般三角形,但角平分线所在的直线即对称轴.如图13,求BM+MN的最小值首先转化为求BM+MN′的最小值,根据垂线段最短,进而转化为求垂线段BH的长度,再一次通过“化折为直”解决问题.

图13

经过以上铺垫,我们再来看看近年中考压轴题,学生是否更容易解决呢?

片段4 广州市18年中考题第23 题第(3) 问: 如图14, 在四边形ABCD中, ∠B= ∠C= 90°,AB > CD,AD=AB+CD,DE平分∠ADC交BC于点E.若CD= 2,AB= 4, 点M,N分别是AE,AB上的动点,求BM+MN的最小值.(前两问已证AE⊥DE,AE平分∠DAB)

图14

虽然背景被换成了梯形,但这里出现了角平分线这个对称轴,为解决问题指出了思路.如图15,经过轴对称变换,求BM+MN的最小值被转化为求GM+MN的最小值,进而转化为求垂线段GH的长度.

图15

以上几题的通法是: 可看做“将军饮马”问题,通过轴对称变换后再“化折为直”,而公理两点之间线段最短(垂线段最短)则是共性.虽然把基本图形放入三角形、正方形、梯形、圆等不同载体,经过迁移、拓展、补充后,给学生带来了较大的挑战,但经过类比、转化、变换等数学思想和方法的分析推理,让人望而生畏的压轴问题得到解决.这一过程将极大地激发学生的学习兴趣和自信心,长此以往,思维必然得到发展,直观想象素养将得到提升.

3.2.2 利用用图形的旋转变换,解决求证线段数量关系的问题

案例2如图16,已知正方形ABCD,将一个45 度的角α的顶点放在D点并绕D点旋转,角的两边分别交AB边和BC边于点E和F,连接EF.你能找到线段EF、AE和CF之间的数量关系吗?

图16

这是“平行四边形”单元里一道很经典的题目, 八年级时可以通过截长补短法添加辅助线, 九年级则可以使用旋转变换添加辅助线.如图17, 把ΔADE绕点D逆时针旋转90°得到ΔDCG, 这里注意要证F、C、G三点共线.易证ΔDEF∽= ΔDGF, 即两者关于DF轴对称, 最终得到EF=AE+CF.当出现共端点、等线段时,可通过旋转三角形,将所求线段集中在一起,从而方便研究,我们可以把这一过程看做一种基本模型.学生掌握这一模型后,教师可在各种变化的情境中考查学生,将有助其直观想象素养的提升.

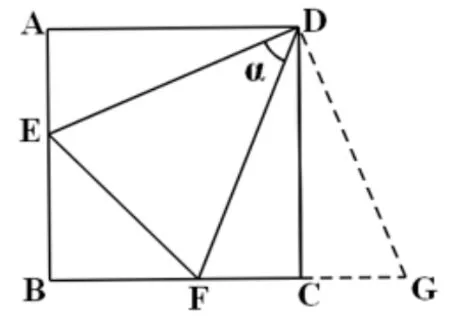
图17

片段1 如图18,已知等边ΔABC及其外接圆,D为劣弧AB上一点.请问弦DC、DA、DB之间有什么数量关系?

图18

解析: 如图19,可以先将ΔCAD绕点C逆时针旋转60°至ΔCBD′处,记得证明D、B、D′三点共线,此时所求三条线段被转化到等边ΔDCD′内,最终得到DC=DA+DB.此题通过三角形的旋转,得到特殊三角形(等边三角形),从而把线段集中在同一个三角形中进行研究,问题得以解决.

图19

还可以把等边ΔABC改为等腰直角ΔABC考查学生,求证即2016年广州中考压轴题.此题仍然是通过旋转得到特殊三角形(等腰直角三角形),从而证明线段之间的关系.

在2020年广州中考第24 题中,再次出现此类基本图形.如图20,⊙O为等边ΔABC的外接圆,半径为2,点D在劣弧AB上运动(不与点A、B重合),连接DA、DB、DC.四边形ADBC的面积S是线段DC的长x的函数吗? 如果是,求出函数解析式;如果不是,请说明理由.

图20

虽然此题是求函数关系,但实质仍然是通过旋转得到等边三角形,从而得到数量(函数)关系,解析如图21 所示.

图21

片段2 如图22,在RtΔACB中,∠ACB= 90°,AC=BC,∠DCE= 45°,请问线段AD、DE、EB之间有什么数量关系?

图22

解析: 如图23,可以把ΔCAD绕点C逆时针旋90°转至ΔCFB处,易证ΔCDE∽= ΔCFE,即两者轴关于CE对称,因此线段AD、DE、EB被集中在RtΔBEF中,从而得到三者的关系为AD2+BE2=DE2.

图23

经过上面几题的铺垫,我们来挑战2018年广州中考题压轴题.

片段3 如图24, 在四边形ABCD中, ∠B= 60°,∠D= 30°,AB=BC.连接BD, 你知道AD,BD,CD三者之间的数量关系吗?

图24

解析: 如图25, 先把ΔABD绕点B顺时针旋转60°至ΔCBD′处, 连接DD′, 得到等边ΔBDQ, 且线段AD,BD,CD被集中在RtΔDCQ中, 从而得到三者的关系为AD2+CD2=BD2.

图25

在以上几题中, 三角形旋转基本模型被放入特殊三角形、特殊四边形、圆等具有对称性的载体中进行研究.当出现共端点、等线段时,可通过旋转变换,把所求线段集中在某个特殊三角形中,是通法.基本图形旋转后能得到特殊三角形(等腰、直角三角形),从而得到线段数量关系是共性.这种对基本图形的迁移、拓展、补充等的训练,符合学生的认知水平和发展规律,这种对图形的动态描述和研究,对激发学生创造力,培养高阶思维,提升直观想象素养将大有裨益.

4 总结与展望

在教学中通过游戏活动和对基本图形进行迁移、拓展、补充等训练,提升初中生直观想象素养的教学策略,经过笔者近两年的实施,所任教班级的学生在几何方面的兴趣和成绩均高于代数部分,尤其是学习基础和习惯良好的同学,优于本年级其他平行班的同档次学生,说明本策略对中等及以上的同学效果明显.但笔者同时也发现,部分学生受文字阅读理解和数学语言表达能力的限制,不能正确理解题目,导致无法完成解答.因此对学生进行文字、符号、图形之间的转换训练,为思维训练扫清障碍,将成为笔者下一步研究的目标.

初中生直观想象素养的提升是一个系统的、长期的、全面的过程,本文以图形的变化作为突破口,希望对这方面的研究起到抛砖引玉的作用.