基于林分高度及郁闭度的森林生物量和蓄积量模型研究

吴发云,高显连,周 蓉,王鹏杰,付安民

(1.国家林业和草原局调查规划设计院,北京 100714；2.北京林业大学,北京 100083；3.中国林业科学研究院资源信息研究所,北京 100091)

森林生态系统是陆地生物圈的主体,是陆地上物质最丰富、结构最复杂的生态系统[1-2]。森林生物量能够直接反映森林碳储量的大小,对减缓全球气候变化有着极为重要的作用[3-4]。蓄积量是林分中所有林木的材积之和[5],不仅能够反映森林资源的丰富程度,也是林业经营的重要决策依据[6]。

激光雷达(light detection and ranging,LiDAR)作为一种主动式遥感技术被广泛地应用在林业中[7-8],其工作原理是利用激光的冠层穿透能力获取森林高度的垂直结构参数。目前,基于激光雷达技术获取森林生物量、蓄积量等森林信息取得了大量的研究进展[9-13]。如:穆喜云等[14]利用机载激光雷达数据提取的植被分位数高度变量及密度变量,构建了基于LiDAR参数的生物量回归模型,并生成了整个区域的地上生物量分布图；罗洪斌等[15]采用不同采样尺寸下的激光雷达参数,建立了云南省橡胶林地上生物量模型,实验结果表明,采样尺度对生物量的估测精度有一定的影响。

卫星及航空影像立体观测数据也被广泛应用于森林结构参数的获取中,其工作原理是通过获取森林冠层顶部的高程信息,结合林下地形及实测数据等,以实现森林高度参数的获取。Persson等[16]结合WorldView-2卫星数据及瑞典Remningstorp地区、Krycklan地区的实测样地数据,建立了胸高断面积加权平均高树高模型。实验结果表明:分别建立的两个森林条件不同地区的模型,其R2均在0.9以上,WorldView-2卫星数据能够适用于估测树高。倪文俭等[17]基于激光雷达数据获取的DEM及CHM数据,验证了高分二号立体观测数据对森林高度估算可行性。实验结果表明,高分二号立体观测数据可用于森林高度的估算。Neigh等[18]探究了IKONOS立体观测数据测量森林冠层高度的可行性。分别获取基于机载激光雷达、高光谱和热成像仪获得的CHM数据、冠层高度数据,基于这3个不同角度的IKONOS立体观测数据获取DSM数据,并进行比较。实验结果表明,IKONOS立体观测数据在森林冠层高度模拟上具有一定的可行性。

如何通过地面样地数据建立林分平均高和郁闭度来准确估测地上森林生物量和蓄积量的模型,从而为激光雷达和立体影像航天航空遥感技术反演大区域的森林蓄积量和生物量提供技术支撑,这是目前亟待解决的问题。本文将利用湖南湘西地区杉木地面样地数据,分析杉木林分平均高、郁闭度、株数之间的相关关系,并采用不同的形式进行因子变量组合,构建多种函数形式的杉木地上生物量模型和蓄积量模型,以此为激光雷达和立体影像航天航空遥感技术在森林地上生物量、蓄积量估测方面提供有力支撑。

1 研究区数据及数据预处理

本文以湖南省湘西地区为研究区域,其地理坐标为北纬27°44.5′～29°38′,东经109°10′～110°22.5′。在研究区内设置半径为15m的圆形样地,开展地面样地调查。本文拟探究林分高度、郁闭度与林分蓄积量、地上生物量之间的关系,因此从地面调查数据中筛选出林分郁闭度C、林分优势木算术平均高HH、林分优势木断面积加权平均高HD、蓄积量V、地上生物量AGB等5类因子进行模型的研建。根据林分郁闭度对样地数据进行分类统计,52个样地实测数据中包含了7个不同的郁闭度。样地数据的统计结果如表1所示。

表1 样地数据情况统计表Tab.1 Statistical table of plot data

2 方法

2.1 相关因子组合

卢振龙等[19]认为不同因子的变量组合具有一定的实际意义,能够弥补单一因子在建模过程中带来的不足；符利勇等[20]从胸径、树高、枝下高等林分变量中选取不同的变量,分别构建多种形式的南方马尾松地上生物量模型；王文栋等[21]分别构建了基于D2×H变量的天山林区6种灌木林生物量估测模型；罗永开等[22]基于单木的树高、冠幅等因子,分别建立了各器官、地上及总生物量的估算模型,实验结果表明幂函数、线性函数具有较好的表现。

因此,为了更详细地探究林分郁闭度、林分高度对蓄积量、地上生物量模型构建的影响,以林分郁闭度C、优势木平均高HH、优势木断面积加权平均高HD为基础,对因子进行变量组合,并引入林分株树N以丰富组合形式。具体变量组合如表2所示。

表2 变量组合表Tab.2 The table of variables combination

2.2 异常数据筛选

为了避免异常数据对实验结果的影响,分别将表2中各组合因子作为自变量,将地上生物量、蓄积量作为因变量,构建因变量与自变量的散点图,对偏差较大的点进行相关原因分析。其中:蓄积量作为因变量的数据中,筛选出2个异常值；地上生物量作为因变量的数据中,筛选出3个异常值。

2.3 模型构建

基于前述因子组合变换及异常数据筛选的基础上,采用SPSS软件分别构建基于郁闭度和林分树高组合因子的地上生物量和蓄积量的线性回归模型、幂函数回归模型、指数函数回归模型及对数函数回归模型,各模型的原始表达式如表3所示。

表3 模型原始表达式Tab.3 The original models expression

2.4 模型评价指标

为了更加直观地对各模型的精度进行评价,本研究采用决定系数R2作为各模型的评价指标。

决定系数(R2):

(1)

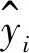
3 结果

将湖南湘西地区52块样地数据分为训练集及测试集。其中,70%作为训练数据集,30%作为测试数据集。采用SPSS软件开展模型构建。

3.1 地上生物量模型

以不同的因子组合形式分别构建了一次函数地上生物量模型、幂函数地上生物量模型、对数函数地上生物量模型和指数函数地上生物量模型,各模型拟合结果如表4所示。

从表4可以看出:

表4 不同变量组合的地上生物量模型回归结果统计Tab.4 Statistics of regression results of aboveground biomass model with different variable combinations

1)以林分郁闭度C、林分优势木算术平均高HH、株数N作为因子的自变量组合变量,其构建的一次函数、幂函数、对数函数、指数函数的各模型的决定系数R2的范围分别为0.301～0.682,0.574～0.861,0.417～0.682,0.310～0.908。其中,以ln(C×HH2)、log(C×HH2)为自变量构建的指数函数模型表现最佳,其R2均为为0.908。

2)以林分郁闭度C、林分优势木断面积加权平均高HD、株数N作为因子的自变量组合变量,其构建的一次函数、幂函数、对数函数、指数函数的各模型的决定系数R2的范围分别为0.306～0.667,0.536～0.843,0.314～0.667,0.316～0.843。其中,幂函数模型中以C×HD2为自变量的模型,指数函数模型中以ln(C×HD2)、log(C×HD2)为自变量的模型拟合效果最佳,决定系数R2均为0.843。

总体来说,以林分郁闭度C、林分优势木算术平均高HH作为自变量构建的组合因子ln(C×HH2)、log(C×HH2)拟合的指数函数地上生物量模型表现最佳。其中,ln(C×HH2)是以e为底的特殊的log(C×HH2)变量的表现形式,因此选用ln(C×HH2)作为最佳组合因子,具体表达形式为:

y=55.566e0.8728×ln(C×HH2)

(2)

图1表示,当ln(C×HH2)作为自变量时,测试数据集的实际地上生物量与预测值的对比分析结果。

图1 地上生物量模型预测值与实测值回归分析Fig.1 Regression analysis of aboveground biomass model predicted values and measured values

3.2 蓄积量模型

以不同的因子组合形式分别构建的一次函数、幂函数、对数函数、指数函数等不同函数形式的蓄积量模型的拟合统计结果,具体情况如表5所示。

从表5可知:1)以林分郁闭度C、林分优势木算术平均高HH、株数N作为因子的自变量组合变量,其构建的一次函数、幂函数、对数函数、指数函数各模型的决定系数R2的范围分别为0.288～0.705,0.556～0.893,0.386～0.705,0.304～0.906。其中:以C2×HH2×N为自变量构建的一次函数蓄积量模型拟合效果最差,决定系数R2为0.288；以ln(C×HH2)、log(C×HH2)为自变量的指数函数蓄积量模型表现最佳,决定系数R2均为0.906。2)以林分郁闭度C、林分优势木断面积加权平均高HD、株数N作为因子的自变量组合变量,其构建的一次函数、幂函数、对数函数、指数函数各模型的R2范围分别为0.299～0.697,0.544～0.878,0.308～0.697,0.311～0.878。其中:以C2×HD2×N为自变量构建的一次函数蓄积量模型表现最差,决定系数R2为0.299；以ln(C×HD2)、log(C×HD2)为自变量的模型拟合效果最佳,决定系数R2均为0.878。

表5 不同变量组合的蓄积量模型回归结果统计Tab.5 Statistics of regression results of accumulation model of different variable combinations

综上所述,在蓄积量模型中,表现最佳的为以ln(C×HH2)、log(C×HH2)为自变量的指数函数蓄积量模型,这与前文中地上生物量模型的结果一致。由于ln(C×HH2)、log(C×HH2)两个变量组合之间具有一定的联系,且ln(C×HH2)是以e为底的特殊的log(C×HH2)变量的表现形式,因此,采用以ln(C×HH2)为自变量的指数函数蓄积量模型表现最佳。其表达式为:

y=0.05e0.979×ln(C×HH2)

(3)

图2表示,当自变量为ln(C×HH2)时,测试集数据的实测蓄积量与预测蓄积量之间的对比结果。

图2 蓄积量模型预测值与实测值回归分析Fig.2 Regression analysis of accumulation model predicted values and the measured value

4 结论与讨论

本文以湖南省湘西地区的地面调查数据为基础,探究了地面样地调查数据中林分郁闭度C、林分优势木算术平均高HH、林分优势木断面积加权平均高HD及株数N与林分蓄积量、林分地上生物量之间的关系,构建了一次线性函数、幂函数、对数函数、指数函数多种森林结构参数估测模型,主要结论如下:

1)综合对比各模型的拟合结果可知,以指数函数为基本模型结构的地上生物量模型、蓄积量模型的表现优于其它函数结构模型。从模型拟合的平均R2来看,幂函数模型具有一定的优势,其平均决定系数R2较高,但从R2最大值来看,拟合效果最佳的为指数函数模型。

2)基于林分郁闭度C、林分优势木算术平均高HH,以及基于林分郁闭度C、林分优势木断面积加权平均高HD构建的对数形式的组合变量——ln(C×HD2)、log(C×HD2)、ln(C×HH2)、log(C×HH2)对地上生物量、蓄积量有很好的解释,基于对数形式的组合变量的地上生物量模型、蓄积量模型的拟合效果最佳。

3)基于对数形式的指数函数模型对变量具有更好的解释。对比24种不同变量组合形式构建的4种不同函数形式的96种地上生物量模型和96种蓄积量模型可知,以ln(C×HD2)和ln(C×HH2)作为自变量构建的指数函数模型对数据具有最佳解释性。

本研究所构建的模型,虽然能够较好地估测地上生物量及蓄积量,但实验数据不够充分,未能深入地探究幂函数与指数函数模型之间的优劣性。如何将其它地面调查数据与林分平均高、郁闭度相结合,进一步提升估测精度,并对其它森林结构参数进行估测,这是今后应研究的内容。