四边形中的中考题型

文 曹 丹

一、根据特殊四边形的性质、判定解决简单问题

四边形是“图形与几何”领域的重要内容之一，其包含平行四边形、矩形、菱形、正方形等特殊四边形。这部分内容知识点多，考查形式丰富多样，能力要求跨度大，是同学们复习的重难点之一。

例1（2020·北京）如图1，菱形ABCD的对角线AC、BD相交于点O，E是AD的中点，点F、G在AB上，EF⊥AB，OG∥EF。

图1

（1）求证：四边形OEFG是矩形；

（2）若AD=10，EF=4，求OE和BG的长。

【解析】本题第（1）问中，由菱形性质可得O是BD中点，结合E是AD的中点，由中位线定理得OE∥AB，结合OG∥EF得▱OEFG，由EF⊥AB得∠EFG=90°，根据有一个角是直角的平行四边形是矩形得证。第（2）问中，由菱形可知AB=AD=10，BD⊥AC，又因为E是AD的中点，得，再由线段和差关系可得BG=AB-AF-GF，将问题转化为求AF的长，通过勾股定理可求出，从而求得BG=2。

【总结】本题主要考查了菱形的性质和矩形的判定。四边形中求线段长通常结合勾股定理、线段和差关系等方法求解。

二、四边形与运动变化

例2（2020·浙江嘉兴）如图2，有一张矩形纸条ABCD，AB=5cm，BC=2cm，点M、N分别在边AB、CD上，CN=1cm。现将四边形BCNM沿MN折叠，点B、C的对应点分别为点B'、C'。当点B'恰好落在边CD上时，线段BM的长为________cm；在点M从点A运动到点B的过程中，若边MB'与边CD交于点E，则点E相应运动的路径长为_____cm。

图2

【解析】如图3，当点B'恰好落在边CD上时，由折叠可知，C'N=CN=1，B'C'=BC=2，B'M=BM，∠B'MN=∠BMN，∠C'=∠C，由矩形性质得∠C'=∠C=90°，DC∥AB，所 以∠B'NM=∠BMN，所 以∠B'MN=∠B'NM，所 以B'M=B'N。在Rt△B'C'N中，由勾股定理得B'N=，则。在点M从点A运动到点B的过程中，起始位置如图4 所示，折叠并结合矩形性质得AE=EN。设AE=EN=x，则DE=DC-CN-EN=4-x。在Rt△ADE中，AD2+DE2=AE2，则有22+（4-x）2=x2，解得，所以。如图5，当M运动到MB'⊥AB时，DE'的值最大，DE'=5-1-2=2。

图3

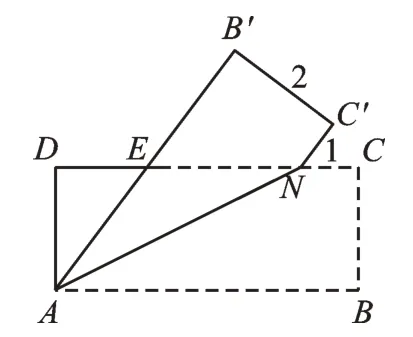
图4

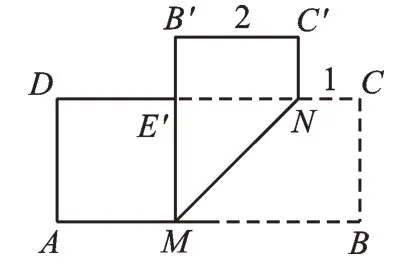
图5

因为MB'与边CD有交点E，当点M运动到如图3 所示位置，即点B'落在CD上时，为运动结束位置，。所以点E的运动轨迹为E→E'→E''，运动路径为。

【总结】本题是矩形折叠问题，考查了翻折、矩形的性质、解直角三角形等知识，解题的关键是理解题意，会综合运用矩形的性质和翻折变换的性质。此外，本题还结合了动点问题，需要我们考虑运动的起始点、转折点和结束点，感受运动的整个过程。

三、平面直角坐标系中的四边形

例3（2020·江苏苏州）如图6，平行四边形OABC的顶点A在x轴的正半轴上，点D（3，2）在对角线OB上，反比例函数（k＞0，x＞0）的图像经过C、D两点。已知平行四边形OABC的面积是，则 点B的坐标为（ ）。

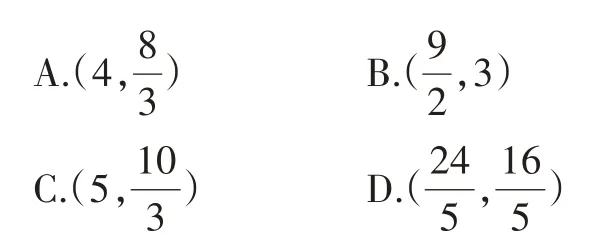
图6

【总结】平面直角坐标系中的四边形问题往往与求点的坐标、函数表达式、面积等知识结合来考查。

四、四边形探究型问题

例4（2020·河南）将正方形ABCD的边AB绕点A逆时针旋转至AB'，记旋转角为α。连接BB'，过点D作DE垂直于直线BB'，垂足为点E，连接DB'、CE。

（1）如图7，当α=60°时，△DEB'的形状为____，连接BD，可求出的值为____。

图7

（2）当0°＜α＜360°，且α≠90°时，

①（1）中两个结论是否仍然成立？如果成立，请仅就图8 的情形进行证明；如果不成立，请说明理由。

图8

②当以点B'、E、C、D为顶点的四边形是平行四边形时，请直接写出的值。

【解析】（1）由题意得AB=AB'=AD，所以∠AB'D=∠ADB'。又因为∠BAB'=60°，所以△ABB'是等边三角形，且∠DAB'=30°，所以∠AB'D=（180°-30°）=75°，所以∠DB'E=180°-60°-75°=45°。又因为DE⊥BE，所以△DEB'是等腰直角三角形。连接BD，如图9，由正方形性质得∠BDC=∠B'DE=45°，所以∠BDC-∠B'DC=∠B'DE-∠B'DC，即∠BDB'=∠CDE，由正方形性质和等腰直角三角形性质得，所以△BDB'∽△CDE，所以。

图9

（2）①连接BD，如图10，因为AB=AB'，∠BAB'=α，所以。因为∠B'AD=α-90°，AD=AB'，所以，所以∠EB'D=∠AB'D-∠AB'B=45°。又因为DE⊥BE，所以△DEB'是等腰直角三角形，所以，由正方形性质可得，∠BDC=45°，所以。因为∠EDB'=∠BDC，所以∠EDB'+∠EDB=∠BDC+∠EDB，即∠BDB'=∠CDE，所以△BDB'∽△CDE，所以。

图10

②以点B'、E、C、D为顶点，没有强调顺序，所以应分类讨论。若E在CD右侧，如图11，以点B'、E、C、D为顶点的四边构成平行四边形，由前面的相似，结合平行四边形性质，得B'C=DE，。又因为，所以。

图11

若E在CD左侧，如图12，则B'E∥CD，所以B'E与AB共线，E与A重合，则。

图12

【总结】本题考查了正方形的性质、平行四边形的性质和判定、相似三角形的性质和判定、等边三角形、图形的旋转等知识点，综合性较强。