西藏地区GDP发展的趋势性研究——基于ARMA模型的预测分析*

安博文 李春玉 刘红卫

（1.新疆财经大学统计与数据科学学院，新疆 乌鲁木齐 830012；2.西藏大学理学院，西藏 拉萨 850000）

1 文献综述

国内生产总值（GDP）是经济社会（国家或地区）在一定时期内运用生产要素所生产的全部最终产品的市场价值，是衡量一个国家或地区经济发展水平的重要指标。精确预测未来十年西藏地区GDP 的增长和增长速度，可以为政府作出经济发展方面的规划提供理论指导。有关GDP的趋势预测方法，国内外学者都进行了广泛研究。从预测模型来看，主要有自回归滑动平均模型（ARMA 模型）、灰色系统模型（GM(1,1)模型）以及一些其他模型。

ARMA 模型是以随机理论为基础的时间序列分析模型，该模型既包含时间趋势的自回归因素，又考虑了时间序列的移动平均因素。因此，在分析GDP的趋势拟合预测上具有独特优势，相关的成果主要有：华鹏和赵学民（2010）针对广东省1978—2008 的GDP发展状况采用ARIMA 模型进行拟合，实证结果发现ARIMA(1,1,0)拟合效果最优，并基于该模型对广东省GDP进行短期预测［1］；熊志斌（2011）采用ARIMA 模型与神经网络集成的时间序列预测算法，对我国1978—2009 年的GDP 数据进行拟合，实证结果显示，集成模型预测结果精度要优于单一模型的预测精度［2］；尹静和何跃（2011）基于四川省2000—2009 年GDP 的季度数据，采用ARIMA-GMDH 组合模型进行拟合，进一步证实了组合模型的预测效果要好于ARIMA 和GMDH单一模型的预测效果［3］；何黎和何跃（2012）对我国GDP 的季度数据分别用GMDH 模型和ARIMA 模型进行预测，在引入PMI 指标后采用ARCH 模型进行预测，实证结果显示，ARCH模型的预测结果要优于GMDH 和ARIMA 模型［4］；张淑红等（2014）基于河南省1978—2010 年人均GDP 指数的时间序列数据，采用AR 模型进行回归预测，研究发现：“十二五”期间人均GDP 增速呈现先慢后快的增长趋势［5］；张静（2017、2018）将贝叶斯先验的统计思想融入时间序列，针对甘肃省1953—2010 年人均GDP 给出了两种先验分布下的贝叶斯算法，并采用稳健的贝叶斯时序模型预测了“十三五”时期人均GDP［6-7］；张强等（2019）基于C-D生产函数和ARIMA 模型构建了GDP 综合预测模型，并充分考虑社会外部环境对模型参数进行调整，对2016—2050 年的GDP 水平进行预测，发现未来区域间发展不均衡的趋势将得到缓解［8］。

GM(1,1)模型是通过建立连续的微分方程，充分利用预测变量的已知信息，弱化未知信息，对灰色系统进行预测分析。大多数学者也将该模型应用到GDP数据的拟合预测上，相关成果主要有：张和平和陈齐海（2017）基于拓展的非线性GM(1,1)幂模型，并结合最新信息优先原则构建了等维新息递补的GM(1,1)模型，对我国“十三五”期间的GDP 总量进行预测［9］；李凯和张涛（2017）采用对初始值进行数据转换和对背景值改进的GM(1,1)模型预测上海市2017—2020年的GDP，发现改进的GM(1,1)模型更适合用于GDP 预测，实证结果显示，未来几年上海市经济水平将保持7%平稳增长［10］；田梓辰和刘淼（2018）采用改进的拉格朗日插值对GM(1,1)模型进行重构，消除了传统拉格朗日插值造成的弊端，并用新疆2006—2015 年的GDP数据进行实证，结果显示，改进的GM(1,1)模型预测精度有所提升［11］；祖培福等（2018）也采用背景值优化的GM(1,1)模型，对牡丹江GDP 进行了预测，发现背景值优化GM(1,1)模型的预测误差要小于传统GM(1,1)模型［12］；龙会典和严广乐（2017）基于GM(1,1)模型和Markov 链模型建立了动态GM(1,1)-Markov 链组合预测模型，用Taylor 展式近似该模型的数值结果，并对1991—2014 年广东省的单位GDP 能耗数据进行拟合预测［13］；张和平和解晓龙（2019）基于数据维度、初始值和原始数据三个维度建立了等维信息GM(1,1)模型、初始改进GM(1,1)模型和拟合模型，并对这3 个模型的权重加以设置得到组合预测模型，通过江西省2004—2015 年的GDP 数据进行实证，结果发现组合优化模型明显提高了预测精度［14］；张敏和党耀国（2018）采用GM(1,1)与AR 相结合的模型对GDP 进行预测，对南京市2000—2015 年GDP 进行小波变换，把原始数据分类，对高频信息用AR 模型拟合，对低频信息用GM(1,1)模型进行拟合，将二者组合得到“十三五”期间南京市GDP的预测情况［15］。

此外，还有部分学者采用其他计量模型对GDP数据进行拟合预测研究。王鑫和肖枝洪（2012）采用干预模型和BP 神经网络集成的时间序列预测模型，对我国1978—2004 年GDP 时间数据进行拟合，实证结果显示，所建立的集成模型对于处理外部事件具有较强的有效性［16］；喻胜华和邓娟（2011）采用主成分分析和贝叶斯正则化的BP 神经网络拟合预测我国1985—2008 年的GDP 数据，研究发现，该组合模型可以简化网络结构，提高模型的泛化能力，预测结果较优［17］；耿鹏和齐红倩（2012）针对高频数据信息损失现象，采用了M-MIDAS-DL 模型对我国1992—2010年的GDP季度数据进行拟合预测，发现该模型在经济趋势分析中具有较好的预测作用［18］；郭秋艳和何跃（2014）基于DFA 计算出的GDP 标度指数，采用BP 神经网络对我国1990—2010 年的数据进行拟合预测，实证发现，该模型适用于非线性、时变性和不确定性的数据［19］；蒋铁军和张怀强（2014）针对我国1952—2010 年的GDP时间序列数据进行相空间重构，采用核主成分回归模型拟合预测，并进一步利用粒子群优化算法提高模型的普适性［20］；索泽辉和冼军（2015）基于Lomb-Scargle周期图法提出GDP指数拟合增长波动率周期、建立指数预测模型，并对1978—2004 年的GDP 数据进行实证分析，发现拟合效果较高、有效性较强［21］；张鹏（2018）基于变权函数和定权函数分别建立线性组合模型，并通过我国1978—2016 年的GDP 数据进行拟合预测，发现权值具有时效性，说明变权组合预测模型更适合时间序列数据［22］；桂文林等（2018）基于奇异谱分析法估计了我国1992—2016 年GDP 产出缺口的季度数据，并通过比较通货膨胀预测性和估计稳定性等方面，发现奇异谱分析法的预测结果要明显优于HP、CF 和BW 等传统滤波方法［23］；冯金平等（2019）将非线性跟踪-微分器采用Taylor 展式加以修正，并通过我国1952—2016 年的GDP 进行实证研究发现，该预测结果要优于依赖模型方法的预测结果［24］。

考虑到西藏地区GDP受到三类产业增加值、政府财政收支、地区进出口贸易、社会消费品零售额和固定资产投资等方面的影响，西藏地区GDP的变动趋势既呈现出影响因素的随机性、又包含时间的波动性，既存在时间上的滞后性、又具有相依性。因此，本文采用ARMA 模型，以1978—2018 年的西藏GDP 数据进行拟合，对未来十年的GDP 发展趋势作出预测，并在预测结果的基础上进行增长速度的分析，认为西藏地区在经济发展的同时还要考虑诸如环境、资源等方面的问题，最终得出未来十年西藏经济将稳步缓慢增长，走向经济增长新常态之路。

2 ARMA模型理论

ARMA 模型广泛应用于时间序列数据，在短期预测方面效果明显。该模型是由Box G 和Jenkins G（1970）首次提出的［25］，ARMA(p,q)模型的具体形式为

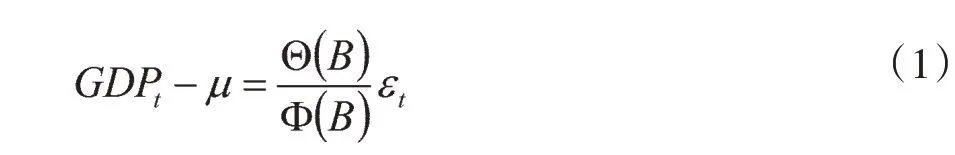
其中：

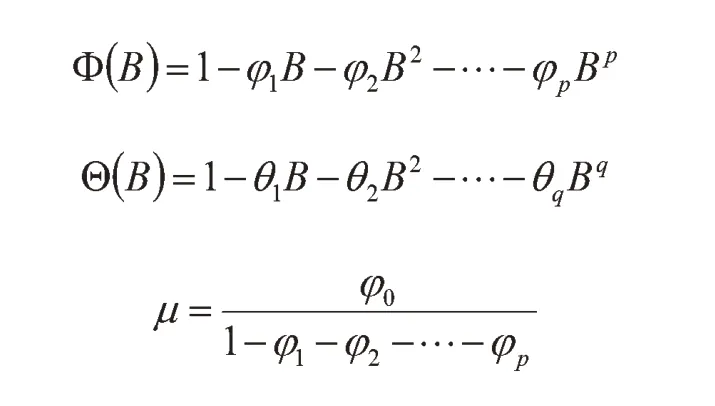
B表示延迟算子，且φp≠0，θq≠0。

平稳性检验是时间序列数据预测的基础，当时间序列数据处于非平稳状态时，可通过取对数或差分进行处理。平稳性检验的方法有两种，一种是通过作时序图和自相关图进行检验；另一种是采用单位根检验。

时序图是一个平面二维坐标图，横轴表示时间，纵轴表示序列取值，可以用来直观分析序列的一些基本分布特征。若时序图显示出该序列始终在一个常数值附近随机波动而且波动的范围有界，则该序列是平稳序列；若时序图显示出该序列有明显的趋势或周期，则该序列不是平稳序列。自相关图（或偏自相关图）是一个平面二维坐标悬垂线图，横轴表示自相关系数（或偏自相关系数），纵轴表示延迟时期数。平稳序列具有短期相关性，即自相关系数随延迟期数的增加，平稳序列的自相关系数会很快衰减向零；非平稳序列的自相关系数衰减向零的速度比较慢。

单位根检验是检验序列平稳性的标准方法，这里采用ADF检验，即建立高阶自回归过程平稳性检验的方程为：

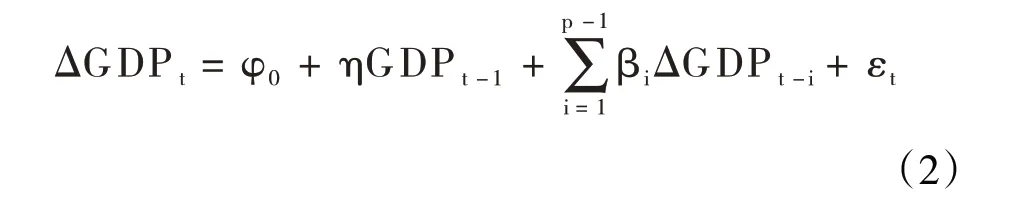
为了保证建模结果的稳健性，需要对GDP序列进行纯随机性检验，构造的检验统计量为：

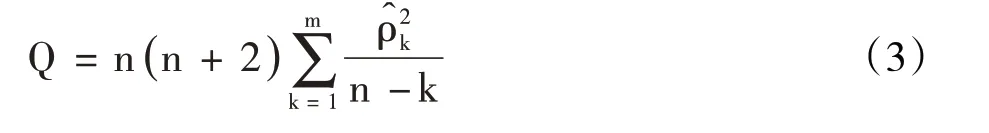
据此提出的原假设为：对∀m ≥1，ρ1=ρ2=···=ρm=0，即延迟期数小于或等于m 期的序列值之间相互独立；备择假设为：对∀m ≥1，∃k ≤m，使ρk=0，即延迟期数小于或等于m期的序列值之间有相关性。

对于ARMA(p,q)模型的估计，从式（1）可以看出，该模型共含有p+q+2 个未知参数，分别为：φ1，…，φp，θ1，…，θq，μ 和。其中μ 是时间序列数据的均值，采用矩估计法有：

下面采用极大似然法估计余下的p+q+1 个参数，即φ1，…，φ，θ1，…，θq，和，得到的估计结果为：

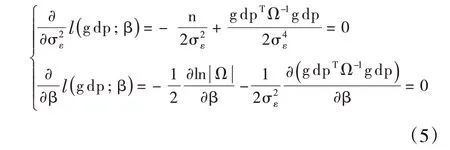
其中：

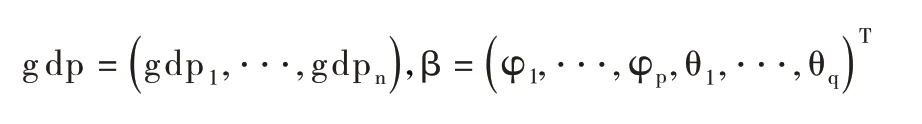
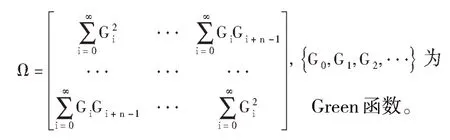
最后，采用最小信息量准则（AIC 准则）选取所有拟合模型中的相对最优模型。该准则可以从两个方面考察拟合模型的优劣：一方面是考虑了拟合程度的似然函数值；另一方面是模型中未知参数的个数，因此AIC准则就是拟合精度和参数个数的加权函数，即

使AIC 函数达到最小的模型被认为是最优模型。从而，当同一个序列可以构造出多个显著有效的拟合模型时，可以根据AIC准则选取相对最优模型。

3 实证分析

3.1 数据预处理

本文样本数据来源于《2019年西藏统计年鉴》，将1978—2018 年西藏地区GDP 的时间序列数据定义为GDPt（t=1978,1979,···,2018），单位为亿元。图1和图2 分别展示了1978—2018 年西藏地区GDP 的定基增长速度与环比增长速度。

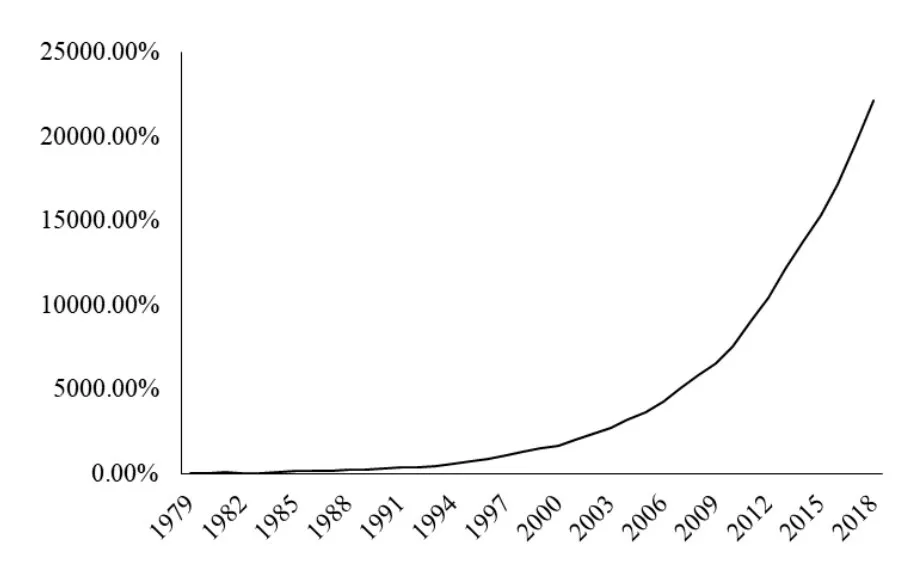
图1 西藏地区GDP定基增长速度

由图1 可以看出，西藏地区GDP 的定基发展速度出现了指数增长的趋势；由图2 可以看出，西藏地区GDP 的环比增长速度波动较大，1982 年和1986 年出现了环比负增长。由于定基增长速度呈现出明显的指数增长趋势，说明原始的GDP 序列属于非平稳序列，并且具有较强的指数增长趋势，因此对原始GDP序列取对数处理，得到：

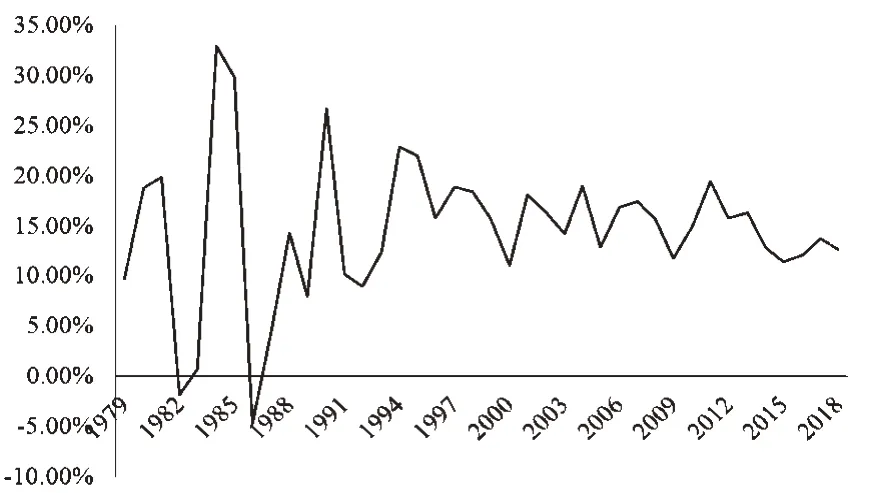
图2 西藏地区GDP环比增长速度

图3 和图4 依次作出了LGDP 序列的时序图和自相关偏自相关图。LGDP 具有明显的直线上升趋势，图4 中LGDP 的自相关系数递减到零的速度缓慢，在较长的延迟期里，自相关系数一直为正，随后一直为负，自相关图中也呈现出了明显的三角对称形，说明该序列是具有单调趋势的非平稳序列。

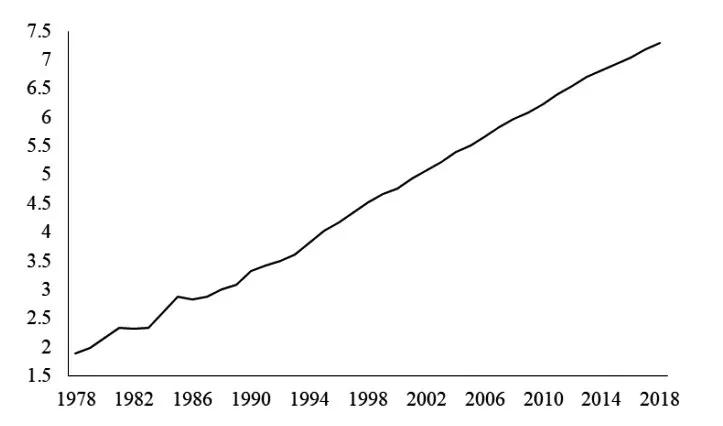
图3 LGDP的时序图

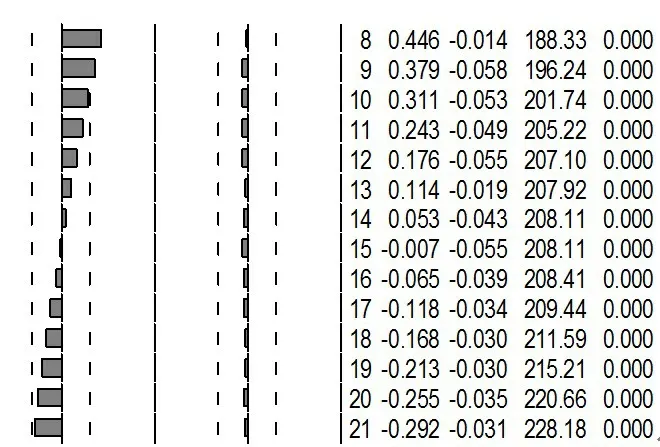
图4 LGDP的自相关和偏自相关图

为消除LGDP 序列的线性趋势性，这里考虑对此作一阶差分处理，即有：

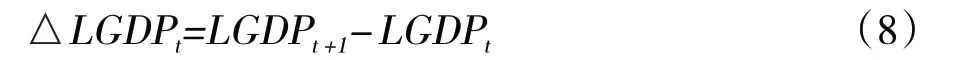
其中：△表示差分算子。从图5 可以发现，△LGDP序列的自相关系数除延迟2 期外都控制在2 个标准差范围以内，说明该序列是一个随机性很强的平稳序列。考虑到时序图检验和自相关偏自相关图检验得出的平稳性结论较为主观，下面采用ADF单位根检验考察△LGDP序列的平稳性。

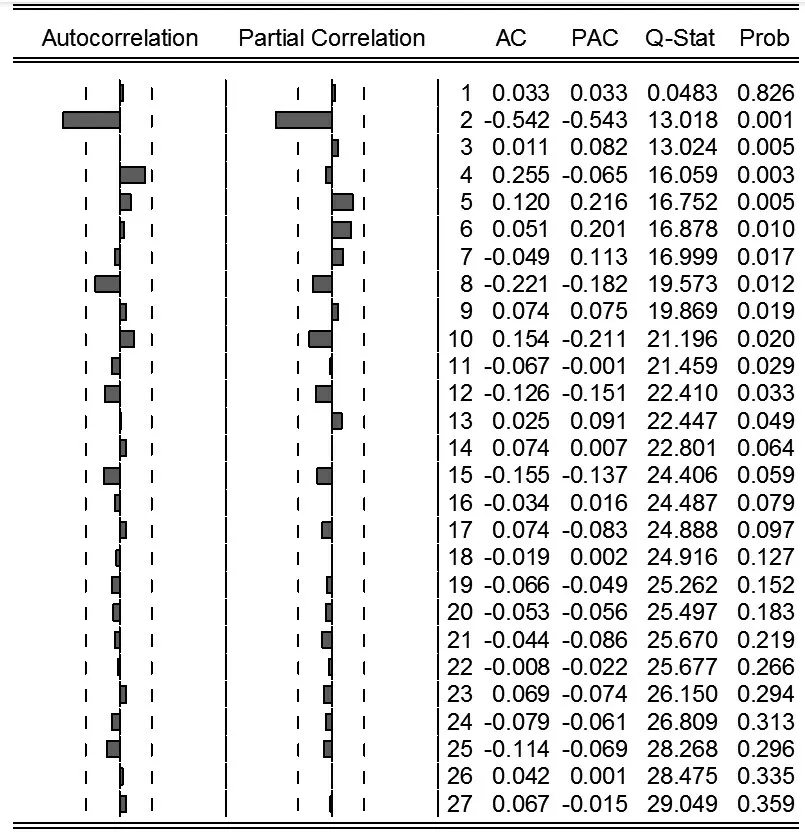
图5 △LGDP的自相关和偏自相关图

根据式（2），可以得到有常数均值但无趋势项类型的ADF 检验结果。表1 的计算结果显示，常数项、滞后一期的LGDP 以及滞后一期的△LGDP 的t 统计量值均在1%水平下显著，ADF检验对应的t统计量值也在1%水平下显著，说明△LGDP 序列属于平稳序列。因此，采用ARMA 模型对该时间序列数据建模得到的估计结果可靠。

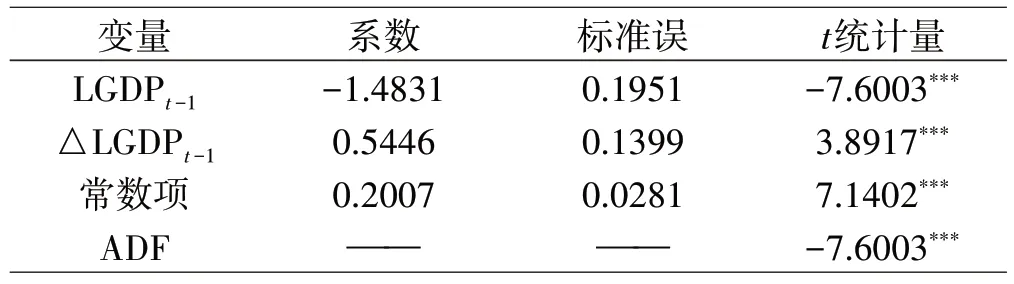
表1 △LGDP的单位根检验结果

这里对△LGDP 序列进行纯随机性分析。根据式（3）计算出延迟2～12 期的Q 统计量值，如表2 所示。当延迟期数为2～5 期时，Q 统计量值在1%水平下显著；当延迟期数为6～12期时，Q统计量值在5%水平下显著。因此，可以显著拒绝原假设，说明△LGDP序列具有很强的前后相关性，即认为该序列趋势有统计规律可循，具备统计建模价值。

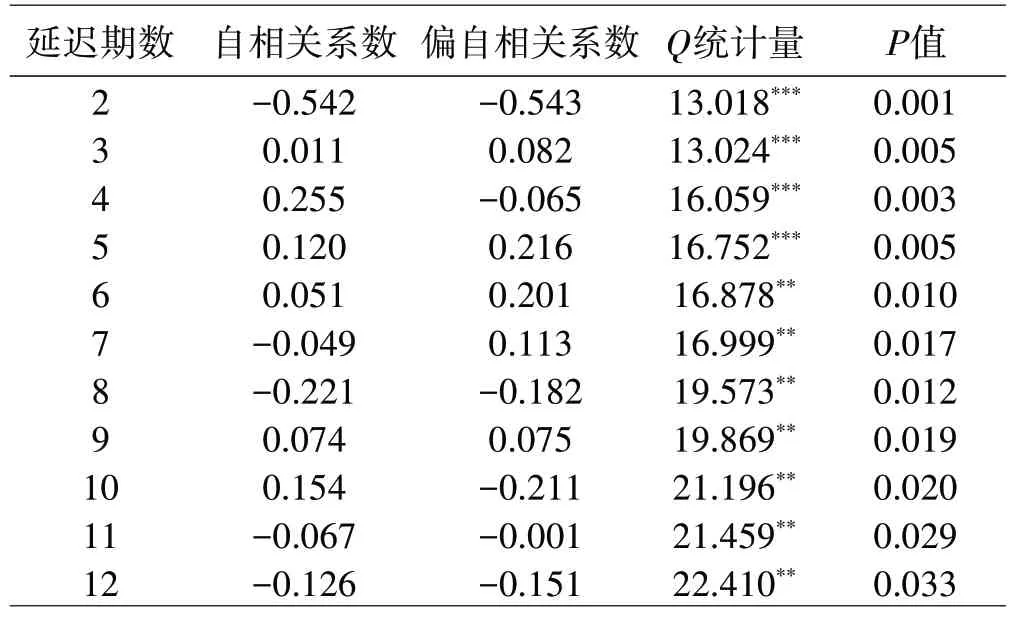
表2 △LGDP的纯随机性检验结果

3.2 模型估计与遴选

估计ARMA 模型的一大关键在于模型的定阶问题。从图5 的自相关和偏自相关图可以看出，自相关系数在2 阶处出现了截尾，可以选用MA(2)模型；偏自相关系数也呈现出了2阶截尾，因此可以采用AR(2)模型；综合考虑自相关系数和偏自相关系数的截尾现象，可以选取ARMA(2,2)模型；自相关系数在延迟4 期处靠近两个标准差的位置，此时考虑用AR(4)模型；同理也可选用ARMA(4,2)模型。因此，下面分别选用AR(2)、MA(2)、ARMA(2,2)、AR(4)以及ARMA(4,2)对△LGDP序列进行拟合，根据式（4）和式（5）计算得到表3。

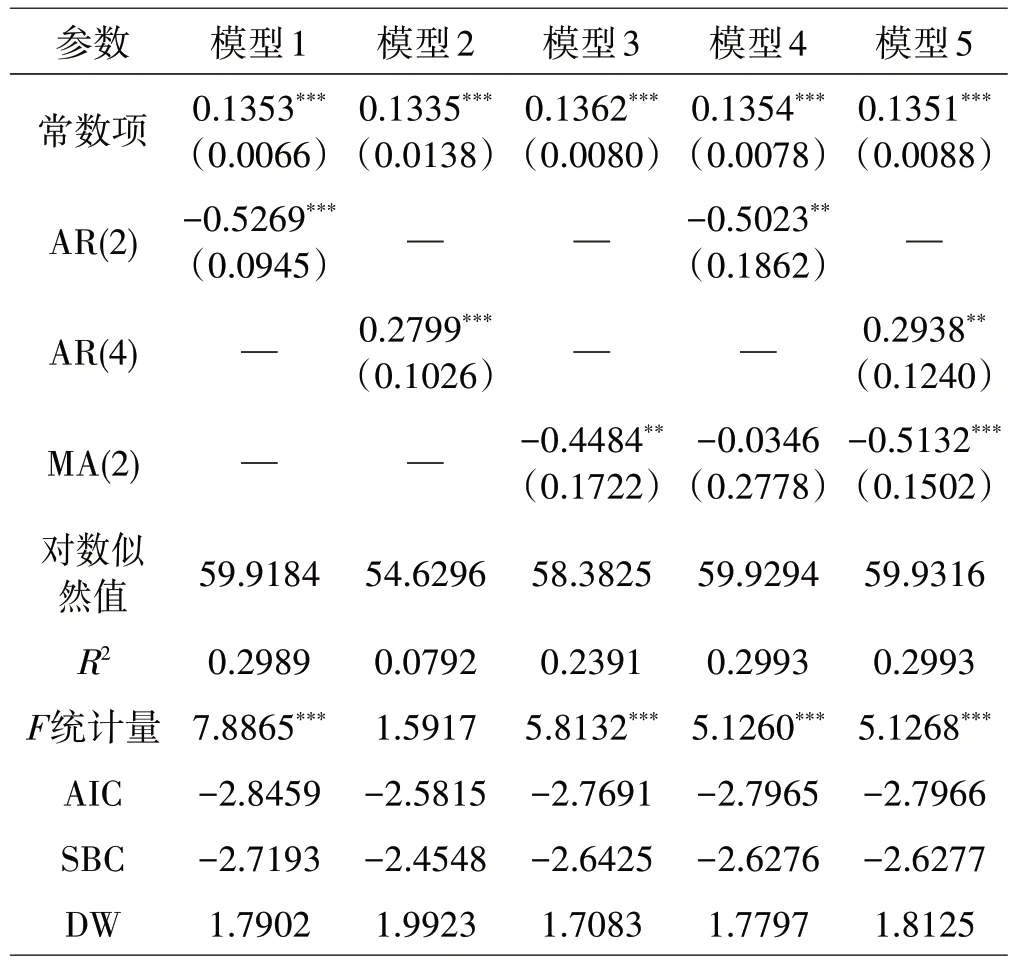
表3 ARMA模型的估计结果

MA(2)模型、AR(2)模型、AR(4)模型以及ARMA(4,2)模型的参数估计结果均在5%水平下显著，说明这4个模型回归结果的可靠性较强，ARMA(2,2)模型中2阶移动平均项系数的回归结果并不显著，说明该模型的可靠性较差，因此舍去该拟合模型。从表3 可以进一步看出，拟合的模型1，即AR(2)模型为：

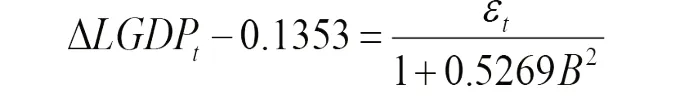
经过化简得到:

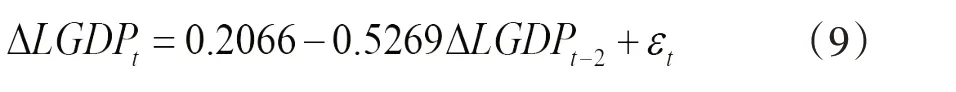
拟合的模型2，即AR(4)模型为:

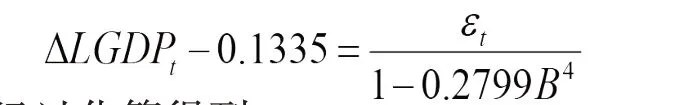
经过化简得到:

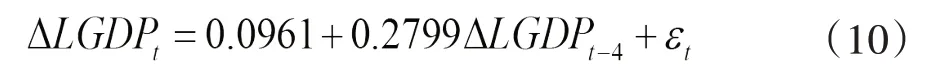
拟合的模型3，即MA(2)模型为:

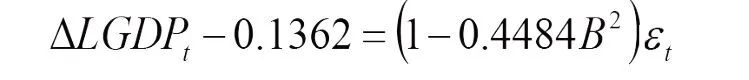
经过化简得到：

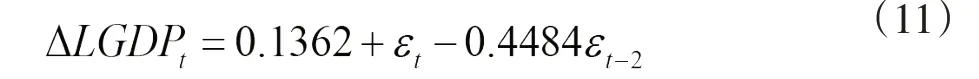
拟合的模型5，即ARMA(4,2)模型为:

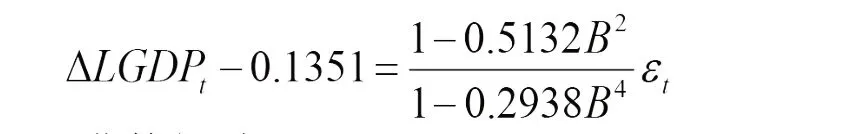
经过化简得到：

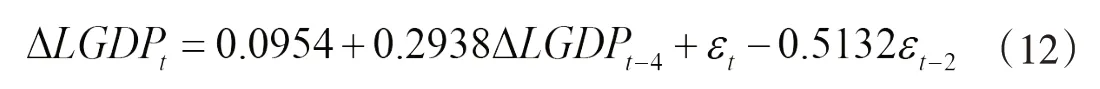
从拟合优度来看，ARMA(4,2)模型要优于AR(2)模型，而AR(2)模型又优于MA(2)模型，AR(4)模型的拟合效果较差；再考虑DW 检验结果，AR(2)模型和MA(2)模型的DW 检验值分别为1.7902 和1.7083，超出了1.8～2.2 的经验范围，故排除这两个模型；对于AR(4)模型与ARMA(4,2)模型，这里同时采用AIC 准则和SBC 准则，ARMA(4,2)模型的AIC 数值和SBC 数值都要小于AR(4)模型的，说明ARMA(4,2)模型要明显优于AR(4)模型。综合以上原因，本文选取ARMA(4,2)模型拟合△LGDP序列，即采用ARIMA(4,1,2)模型拟合LGDP序列。

3.3 稳健性分析与预测

由于估计式(5)时采用了极大似然法，而极大似然估计的前提为假设△LGDP 序列服从正态分布。从图6 可以看出，△LGDP 序列大体上服从正态分布，即符合极大似然估计的前提假设。

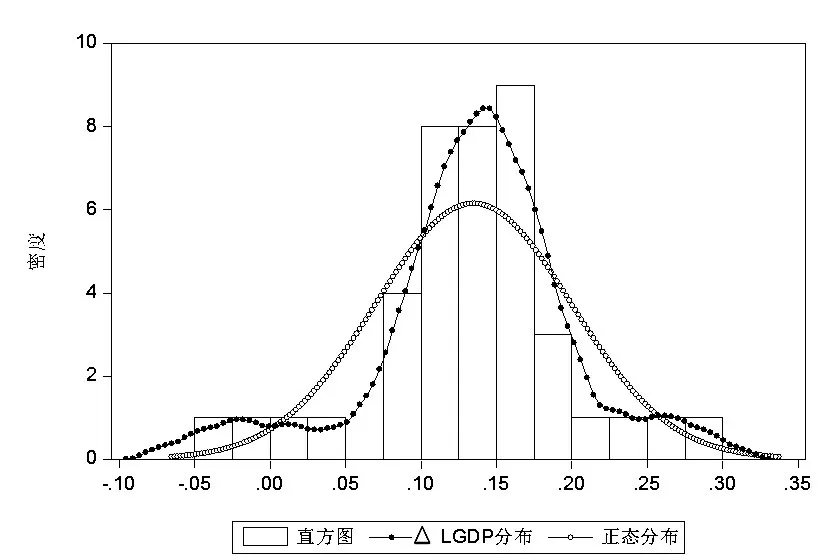
图6 △LGDP的分布直方图

本文最终选定ARIMA(4,1,2)模型拟合LGDP 序列，下面就对残差序列进行纯随机性检验，据此判断ARIMA(4,1,2)模型对LGDP 序列的信息提取是否充分，即判断是否需要对该序列进行再一步挖掘。

从图7和图8可以看出，残差序列符合正态分布的基本假设，下面再对残差序列进行白噪声检验（表4）。

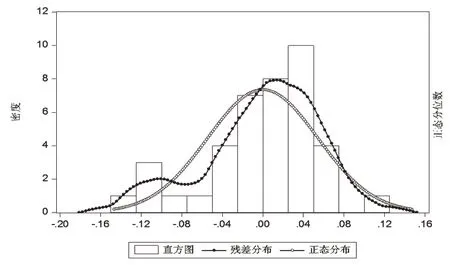
图7 残差序列的分布直方图

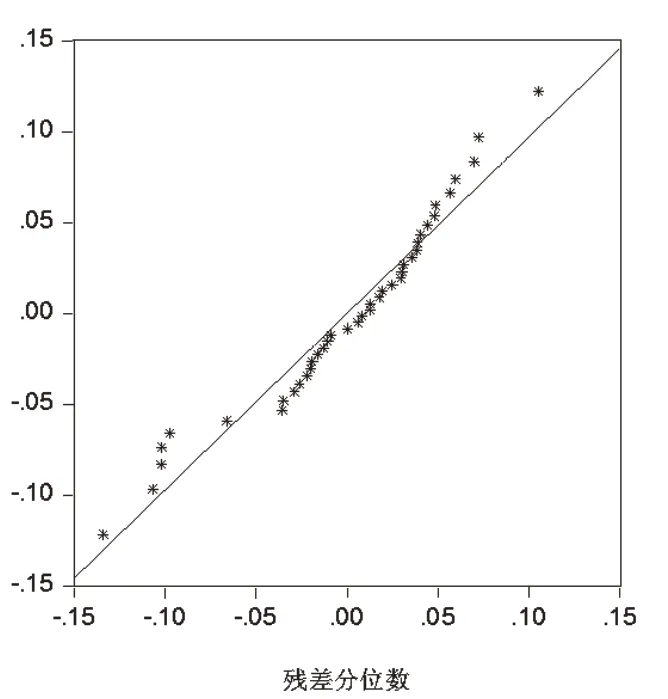
图8 残差序列的正态Q-Q图

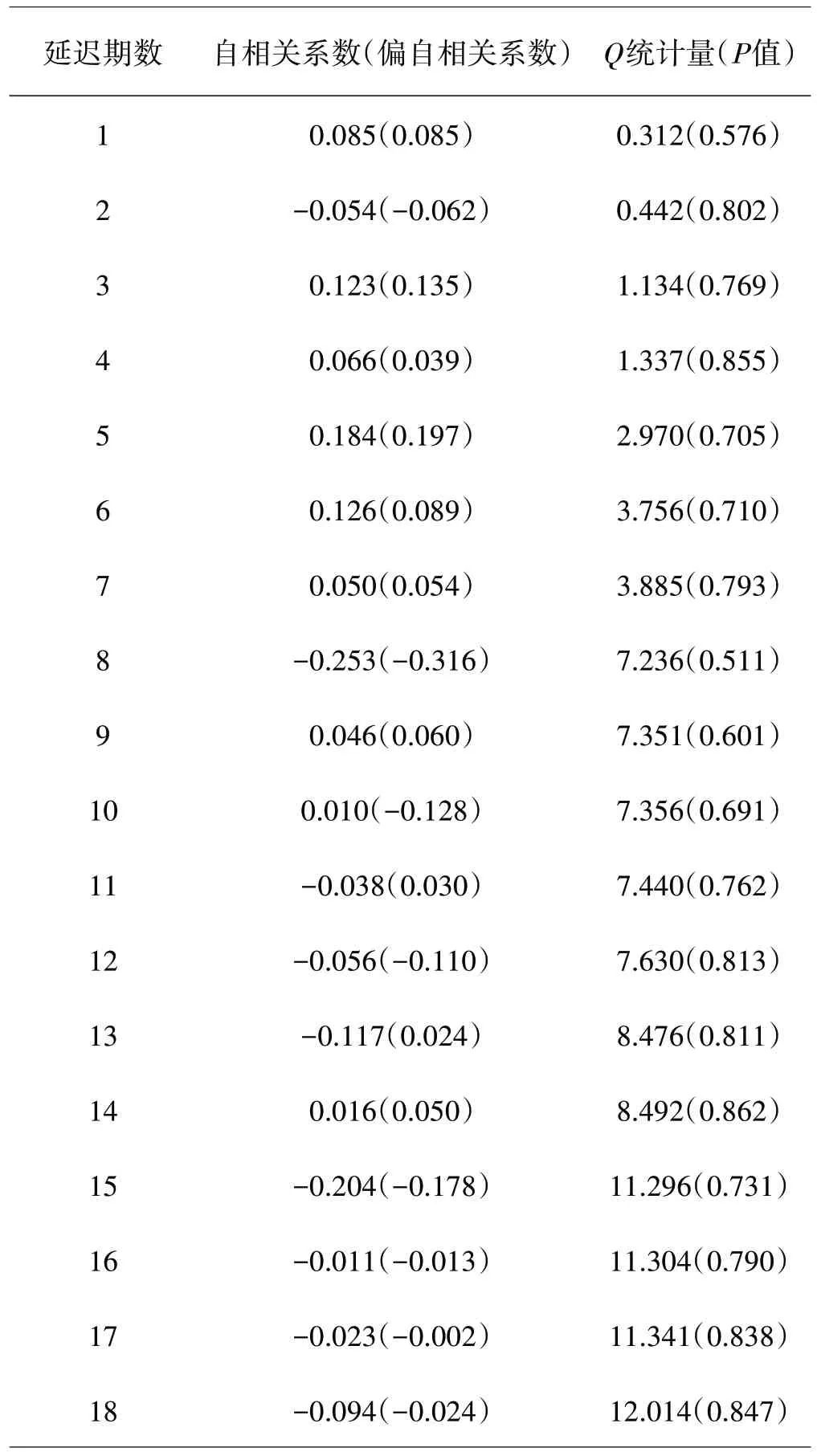
表4 残差的白噪声检验结果

从表4 可以看出，P 值明显大于显著性水平0.05，所以残差序列不能拒绝纯随机的原假设，即认为该序列是纯随机序列。

上述检验结果显示，△LGDP 序列服从正态分布的基本假设，残差序列也通过了正态性检验和白噪声检验，说明采用ARIMA(4,1,2)对LGDP 序列建模，其估计结果是十分稳健的。

下面采用ARIMA(4,1,2)对西藏地区未来十年的GDP 情况进行预测，将式（7）和式（8）代入式（12）中，得到预测方程为：

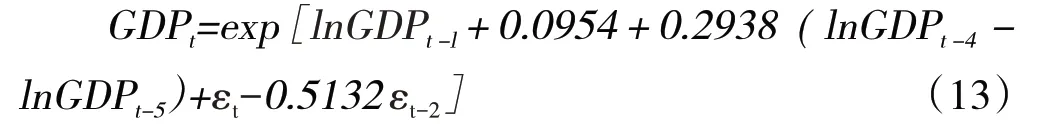
根据式（13）计算出对未来十年西藏地区GDP 的发展情况为：

依据表5 的预测结果，作出西藏未来GDP 的定基增长速度图和环比增长速度图，如图9和图10。

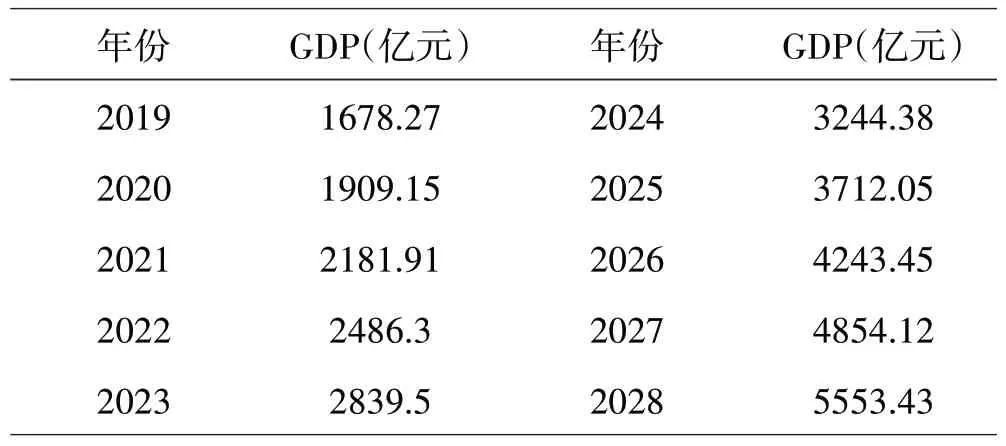
表5 来十年西藏GDP预测结果

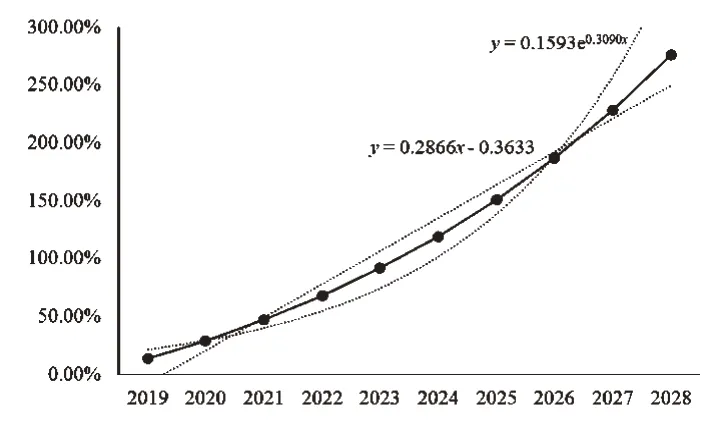
图9 未来十年西藏GDP定基增长速度

从图9 可以看出，未来十年西藏地区GDP 仍处于增长趋势，但定基增长速度已经从图1 的指数增长趋势变得较为平缓，甚至接近于一条直线，说明西藏地区GDP 的增速减缓了。再从图10 可以看出，未来十年西藏地区GDP的环比增长速度虽然呈现上升趋势，但出现了不同程度的波动情况，由2020 年到2021 年的环比增长下降了近0.5个百分点。

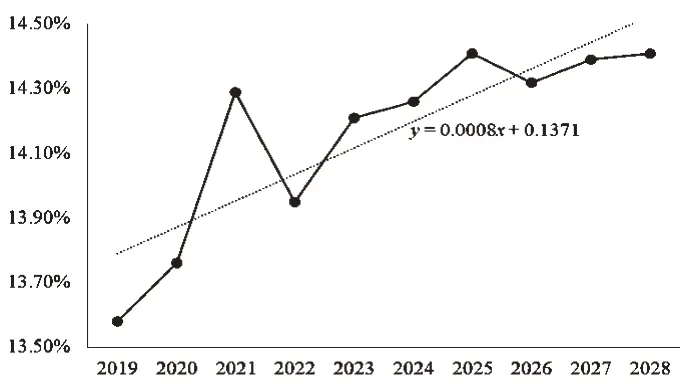
图10 未来十年西藏GDP环比增长速度

4 结论

本文基于西藏地区1978—2018 年的GDP 时间序列数据，建立ARIMA(4,1,2)拟合预测模型。首先，对非平稳GDP 序列进行取对数、作差分的平稳性处理，得到平稳的且具有时期相关性的△LGDP序列；其次，采用ARMA 对△LGDP序列进行拟合，并通过拟合优度、DW 检验、AIC 准则和SBC 准则等统计指标对拟合的模型综合比较，发现ARIMA(4,1,2)对LGDP 序列的拟合效果最好；最后，通过△LGDP序列的正态性检验以及残差序列的正态性检验和白噪声检验，证明了估计结果的稳健性，并对西藏地区未来十年GDP的发展情况进行预测。

实证结果显示，在未来十年西藏地区的经济发展中，西藏GDP定基增长速度呈现出较为平缓的直线增长趋势，环比增长速度也出现了不同程度的下调，从侧面说明了，未来十年西藏地区在经济发展同时，还要考虑到诸如环境、资源等方面的问题，要坚持走经济增长新常态之路。