工业机器人误差补偿运动学算法设计

梁兆东，肖永强，游 玮，葛景国

（埃夫特智能装备股份有限公司，安徽 芜湖 241000）

1 引言

随着国产工业机器人进入涂胶、弧焊、装配等高精度应用，机器人自身绝对定位精度的问题显得十分凸显。工业机器人由于加工装配过程的制造几何参数误差，连杆和关节的柔性，以及减速机齿隙等诸多不可避免的因素导致机器人绝对定位精度差，而其中几何参数误差占据机器人末端误差来源的95%[1]。工业机器人的标定方法及对应的补偿算法是提升机器人的绝对定位精度的一种有效途径，工业机器人的运动学标定过程包括建模、测量、辨识和补偿[2]。运动学标定的过程是指通过修正机器人运动控制器中的运动学模型参数提升机器人绝对定位精度的过程。因此在不改变机器人机械本体的基础上，通过算法补偿实现机器人的绝对定位精度的提升有着重要的研究意义。

以MDH 模型为基础，建立机器人运动学误差模型，通过对几何参数误差进行补偿，采用名义运动学模型和基于雅克比的辨识运动学模型关节角度偏差补偿相结合的逆运动学算法补偿误差，提高了机器人的绝对定位精度。

2 工业机器人MDH 模型和误差模型

工业机器人目前应用最多的运动学模型为DH 模型（Denavit-Hartenberg），但当机器人相邻关节轴线平行或接近平行时，DH 模型不满足连续性。针对DH 模型的缺陷，众多学者提出了其他修正模型。1983 年，Hayati 在相邻平行或者接近平行关节引入了Y 轴的旋转参数β[3]，建立了Modified-DH 模型，即MDH模型。1988 年，Stone 提出了S 模型[4]，使用6 个参数描述相邻关节之间坐标变换关系，模型不具备连续性。文献[5]于1992 年提出了CPC 模型，构建了完整连续的运动学模型，但其引入了冗余参数。2001 年，NTU 的Chen 提出了POE 模型[6]，POE 模型基于旋量理论的指数积，但是此模型表达式与工业机器人控制的接口相对复杂，实际应用较少。

随着近年来国产工业机器人的发展迅速，国内很多高校开展了运动学标定和补偿的相关研究：文献[7]进行了基于POE 方法的工业机器人运动学标定研究；文献[8]开展了工业机器人参数标定方法与实验研究的合作。

采用Hayati 的MDH 模型，通用球形腕的六轴工业机器人中第2 轴与第3 轴平行，因此在第2 轴的模型引入Y 轴的旋转参数β。

DH 模型中相邻连杆坐标系之间的位姿关系的运动学表达式为：

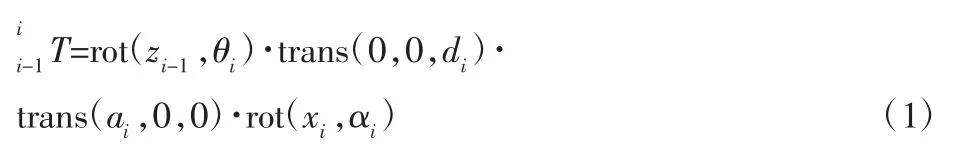
Hayati 的MDH 模型中在相邻平行或者接近平行的关节引入了Y 轴的旋转参数β 后，平行或者接近平行的相邻连杆坐标系之间的位姿关系的运动学表达式为：

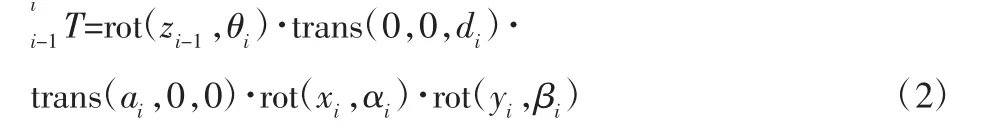
图1 六轴工业机器人运动学模型关节坐标系Fig.1 Joint Coordinates of Six Axis Industrial Robot Kinematics

假设几何误差Δg=（Δθ，Δd，Δa，Δα，Δβ），末端位姿的偏差Δx=（Δpx，Δpy，Δpz，Δφx，Δφy，Δφz），则可以建立考虑几何误差的末端位置偏差的运动学模型，式（3）为名义正运动学模型，式（4）为考虑几何误差后的正运动学模型：

假设Δg 很小，利用小误差模型的线性拟合可以得到几何误差与末端位姿误差之间的误差模型：

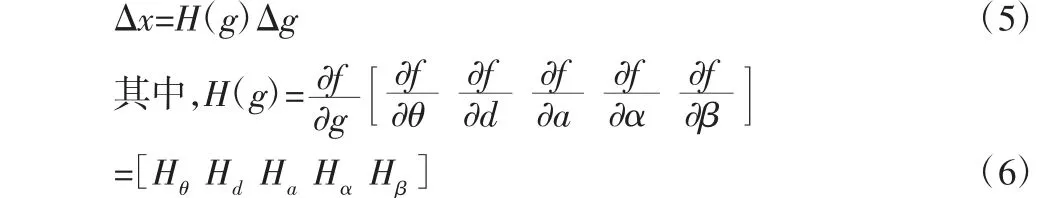
式中：H（g）—几何误差参数Δg 对机器人末端位姿误差Δx 的（6×5n）作用矩阵，称为MDH 模型辨识雅克比矩阵，H（g）每一列代表了机器人末端位姿误差Δx 相对于Δg 中某一几何参数的灵敏性。H（g）利用微分齐次变换求得，而不是通过对式（4）求微分获得。利用激光跟踪仪测量获得机器人末端的实际空间位姿，并将其与机器人控制器名义正运动学模型的位姿值进行求差即得到末端位姿误差，进而利用式（5）可以求得到机器人的几何参数误差Δg。

3 基于误差补偿的运动学算法设计

误差补偿是机器人标定的最后一个步骤，其主要工作是将标定辨识后的几何误差参数Δg，将误差参数导入到机器人控制系统中提高机器人的绝对定位精度。考虑几何误差后，机器人的笛卡尔空间的运动需要对式（4）求逆获得关节空间的各轴驱动角度，但是若几何参数为非名义参数后，六轴机器人运动学模型求逆将是一个求解超越函数的非线性方程组，其求解相对复杂。通用的六轴串联工业机器人（开链结构）只有在满足Pieper 准则中两个充分条件之一才能获得封闭解，封闭解的求解过程相对简单。Pieper 准则六轴串联机器人最后三个关节之间满足αi=0 或者αi=±π/2，因此也有学者提出只补偿几何参数的杆件长度参数ai和di，此时运动学逆解也能获得封闭解，但是补偿精度有限。

为了达到更高的补偿精度，需要将所有的几何误差都予以考虑。目前几何误差补偿方法有笛卡尔空间补偿法和关节空间补偿法。笛卡尔空间补偿常有两种方法：（1）笛卡尔空间误差模型估计，通过误差模型估计笛卡尔空间位姿误差并在笛卡尔空间补偿[9]，再用名义逆运动学求解，此方法较为简单，计算时间短，但是此方法是一种位姿估计，依赖于期望笛卡尔位姿和实际笛卡尔位姿之间微分偏差很小，否则此方法收敛速度很慢；（2）通过外部测量设备测量估计出误差[10]，然后在通过名义逆运动学求解，此方法依赖于昂贵的外部高精度的位姿测量设备（如激光跟踪仪），在实际现场应用不太方便。关节空间补偿法[11]，是通过通过微分运动关系将笛卡尔坐标空间的位姿误差反解到关节坐标空间的偏差，并将其此偏差叠加名义逆运动学模型上。文献[11]采用了基于微分齐次变换的正向误差计算和基于旋量理论求解雅克比的反向误差补偿结合的方法，而采用名义逆运动学、基于齐次变换的正向误差计算和基于几何雅克比反求关节空间偏差相结合的方法，具体求解流程图，如图2 所示。解释如下：

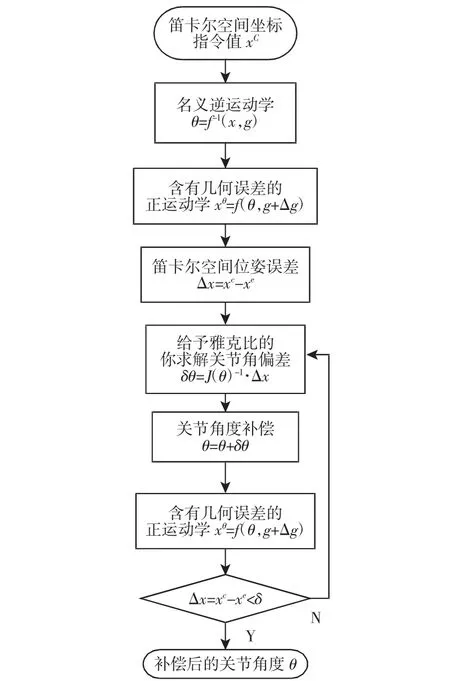
图2 基于误差补偿的运动学算法流程图Fig.2 Flow of Kinematics Based Errors Compensation

（1）首先通过名义逆运动学模型求解笛卡尔空间位姿指令值xc对应的各个关节名义值θ。

（2）然后将第（1）步求解得到的关节名义值代入到考虑几何误差的正运动学模型中，求解考虑几何误差的笛卡尔坐标值xe。

（3）求解笛卡尔坐标误差值Δx=xc-xe。

（4）通过此时关节位置θ 的雅克比矩阵，并将其求逆，与第（3）步得到的Δx 联合求解得到关节空间对应各轴偏差值δθ。

（5）补偿各个关节坐标值θ=θ+δθ。

（6）将第（5）步补偿后的关节坐标值代入到考虑几何误差的正运动学中，求解关节补偿后的笛卡尔坐标值xe。

（7）计算笛卡尔坐标指令值和补偿后的笛卡尔坐标值之间的误差，判断其与指定笛卡尔坐标容许误差δ 比较大小。如果为真进入第（8）步，否则进入第（4）步。

（8）将第（5）步中最新一次补偿的关节坐标值θ 下发到各个轴的位置控制器中。

4 误差补偿算法试验结果与分析

4.1 误差标定试验数据

试验对机器人为埃夫特自主研发的ER3A 六轴工业机器人，其名义的DH 模型参数，如表1 所示。试验中所用验证算法的控制器为埃夫特RP-1 机器人控制器，所用测量设备为LEICA 的AT401 激光跟踪仪，绝对距离测量性能：分辨力0.1μm，精度10μm，重复性5μm。LEICA 激光跟踪仪辨识的ER3A 机器人几何误差参数，如表2 所示。

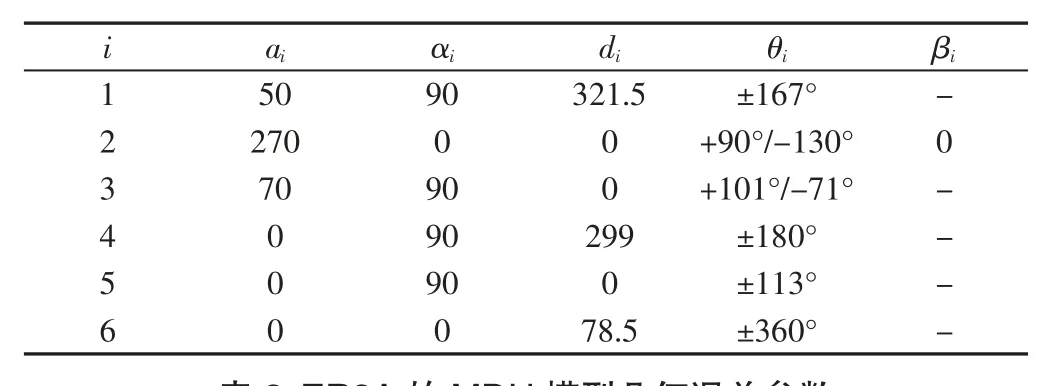
表1 ER3A 的MDH 模型名义参数Tab.1 Nominal Parameters of ER3A MDH Model

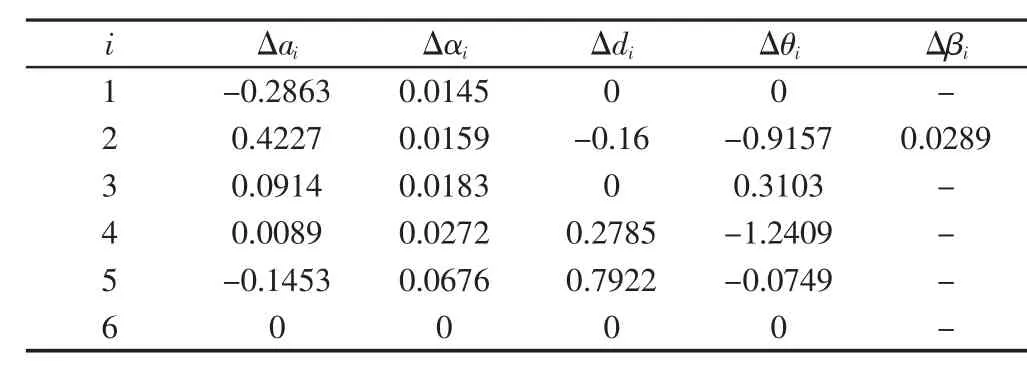
表2 ER3A 的MDH 模型几何误差参数Tab.2 Geometrical Errors Parameters of ER3A MDH

4.2 误差补偿试验与分析

首先选取ER3A 机器人工作空间的350 个点，并在机器人控制器中存储350 个点的笛卡尔坐标位置值。使用机器人名义逆运动学模型和设计的基于误差补偿的运动学算法分别进行试验：试验过程中用LEICA 激光跟踪仪AT401 进行笛卡尔空间的350个点实际空间位置测量，并实时记录350 个点的实际位置值，使用以下方程评价绝对定位精度：

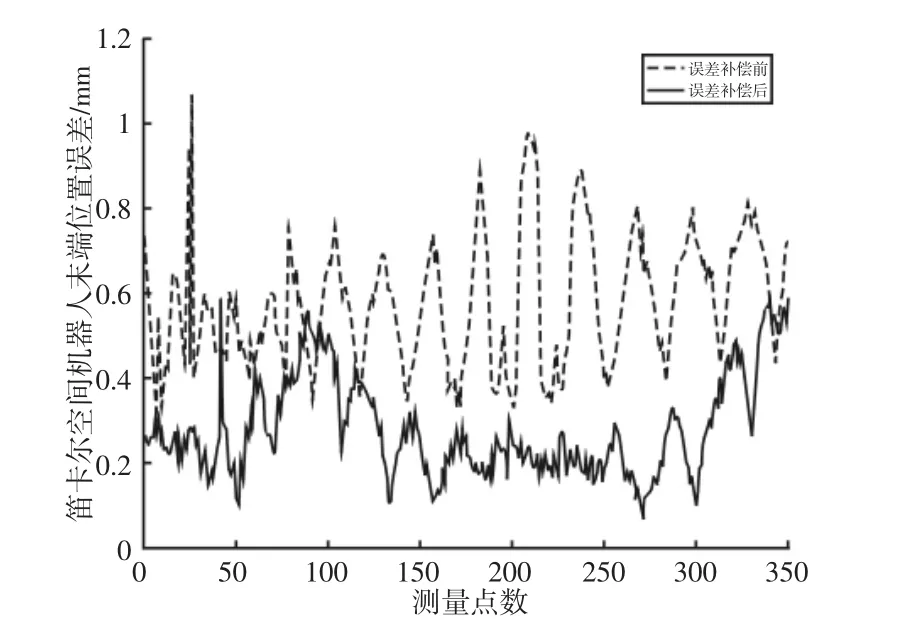
图3 误差补偿前后机器人末端位置误差Fig.3 TCP Errors of Robot TCP with and without Errors Compensation

表3 ER3A 的误差补偿前后的TCP 误差对比Tab.3 TCP Errors Comparison of ER3A with and without Errors Compensation

对比可知，误差补偿后，机器人笛卡尔空间坐标的位置误差的均值从0.5754mm 降低到0.2779mm，位置误差均值降低了51.70%；机器人笛卡尔空间坐标的位置误差的最大值从1.0811mm 降低到0.5887mm，位置误差最大值降低了45.54%，证明了误差补偿的运动学算法的有效性。

5 结论

以MDH 模型为基础，建立了机器人MDH 模型中几何参数误差和机器人末端位姿误差之间的误差模型，提出了基于雅克比矩阵在关节空间补偿因几何误差导致的笛卡尔空间位姿误差的关节偏差的运动学算法，通过此误差补偿提高机器人的绝对定位精度。以自主研发ER3A 机器人为误差补偿算法试验对象进行验证，测量验证点的位置误差均值由0.5754mm 降低到0.2779mm，即在采用提出的误差补偿运动学算法后，ER3A 机器人的绝对定位精度提高了51.70%。该误差补偿运动学算法通过考虑几何误差，建立对应的误差模型并应用运动学算法补偿，有效提高了机器人的绝对定位精度。