车辆主动悬架解耦及其遗传优化控制研究

何 锋，冯子航，吴 清

（1.贵州大学机械工程学院，贵州 贵阳 550025；2.北京理工大学机械与车辆学院，北京100081）

1 引言

车辆悬架系统直接影响车辆行驶的平顺性。对于车辆平顺性的仿真分析，国内外学者进行了广泛研究。这些研究大致分为两步：（1）车辆仿真模型的搭建；（2）控制算法的研究。车轮受到路面激励产生的运动引起车辆簧上质量的振动是一个复杂的耦合过程，需要从整车悬架系统进行考虑。在悬架模型搭建方面，目前许多学者多采用1/4 悬架模型，也有1/2 悬架模型。路面激励建模也是影响整车悬架测试的主要因素，为了简化计算，很多学者建立单轮路面激励或滞后的双轮激励。在控制算法方面，主要有模糊控制、滑膜控制、LQG 控制、微分解耦等。文献[1]对车辆1/4 悬架模型进行遗传粒子群LQG 控制，弥补了单一LQG 控制权重系数选择的不足的缺点；文献[2]在前后悬架耦合关系的基础上提出了分层控制策略，加快了系统的响应速度，大幅降低了CPU 的计算时间；文献[3]通过遗传算法优化了模糊控制器的量化因子及PID参数的修正系数，提高了车辆的平顺性；文献[4]建立了整车悬架模型，并在单一路面激励的基础上对悬架进行最优二次型控制。微分解耦能对悬架系统进行解耦，实现理想输出参数单独控制，遗传算法具有内在的隐并行性和很好的全局寻优能力，能自动获取和指导优化的搜索空间。将MIMO 解耦控制与遗传算法手段相结合是解决单一解耦问题的一个有效途径[5]。

在建立整车主动悬架系统的同时建立了四轮路面激励模型作为输入信号。运用微分几何解耦方法对整车七自由度悬架系统进行解耦并设计反馈控制器，最后通过遗传算法对控制器的二阶方程系数进行全局寻优，使悬架系统目标输出参数的均方根值大幅衰减。

2 整车悬架建模

主动悬架7 自由度整车模型，如图1 所示。

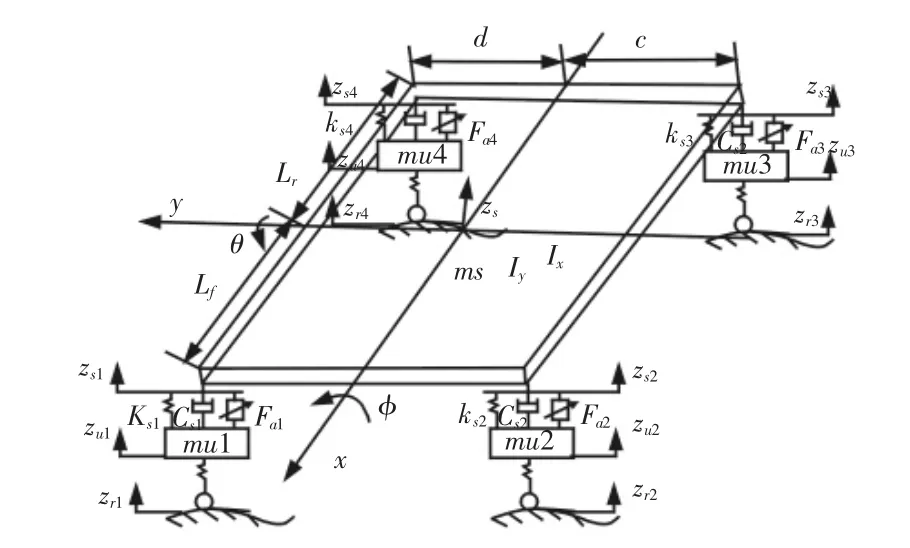
图1 主动悬架7 自由度模型Fig.1 7 degrees of Freedom of Active Suspension

式中：ms—整车簧载质量；mui—非簧载质量；Ix、Iy—整车绕x、y 轴的转动惯量；Lf、Lr—质心到前后轴距离；c、d—质心到左右侧车轮横向距离；θ—簧载质量俯仰角；φ—簧载质量侧倾角；Zs—簧载质心垂向位移；Zri—路面不平度函数；Zui—非簧载质量的垂向位移；Zsi—簧载质量的垂向位移；Kti—轮胎侧偏刚度；Ksi—悬架弹簧刚度；Csi—悬架阻尼系数；Fai—作动器产生的力。

3 四轮路面激励建模

国内外关于整车悬架振动研究的论文，大多基于建立单轮路面激励模型，为提高车辆整车模型的准确性，基于滤波白噪声，建立单轮路面激励时域模型，并根据左右轮迹相干函数和前后轮的滞后性，建立四轮路面空间时域模型。

3.1 单轮路面激励时域建模

根据路面功率谱密度及系统频响函数建立单轮路面激励Z（t）的时域模型[6]

3.2 四轮路面激励时域建模

车辆行驶过程中，左右轮受到的随机路面激励并不相同，一般采用相干函数或者传递函数进行描述，参考文献[6-7]，推导出相干函数数学模型。

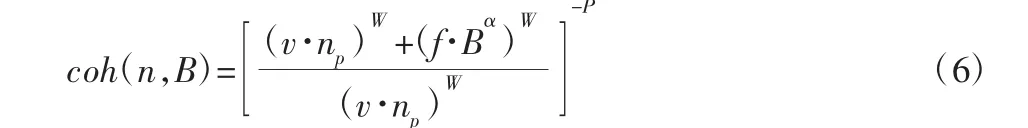
式中：n—空间频率；B—左右车轮轮距；α—路面同性指数；W—频

率梯度；np—参考空间频率；P—梯度指数。

假设车辆匀速行驶，车辆后轮所受路面激励相较于前轮会产生时间延时。

假设车辆行驶在B 级路面，速度v=20m/s。其余参激励数参考文献[7]，由式（5）～式（7）建立四轮路面激励时域模型。

图2 前轮激励时域模型Fig.2 Front Wheel Incentive Time Domain Model

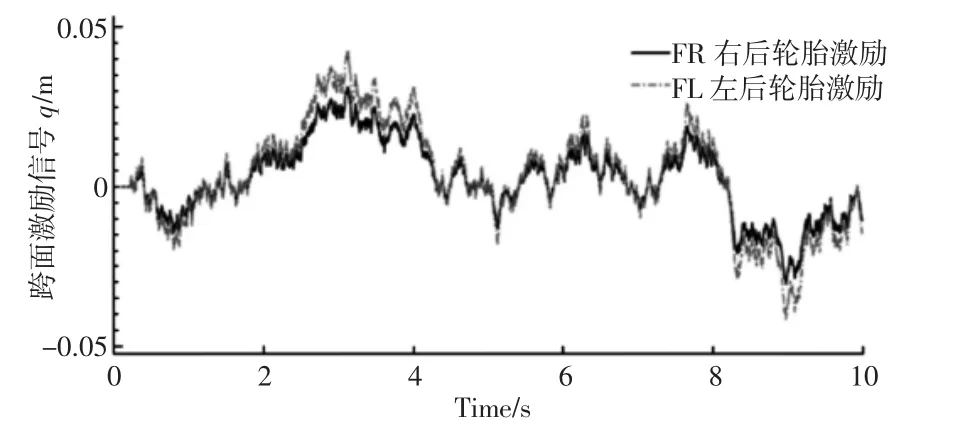
图3 后轮激励时域模型Fig.3 Rear Wheel Incentive Time Domain Model

4 微分几何悬架解耦

4.1 非线性化二阶系统解耦条件

将悬架系统建成15 维状态方程组，MIMO 非线性系统表达式如下[8]：

式中：x=［x1x2… x19］∈Rn—系统的状态变量；u∈Rm由作动器输入：为控制变量，ω=［ω1，ω2，ω3，ω4］∈Rl：为外界干扰信号；h（x）=［Zs；θ；φ；Zu1］—输出信号；f、g、D—非线性光滑向量场。

在x0处非奇异。

4.2 悬架系统解耦控制计算

则系统的解耦矩阵E（x）可以表示为：

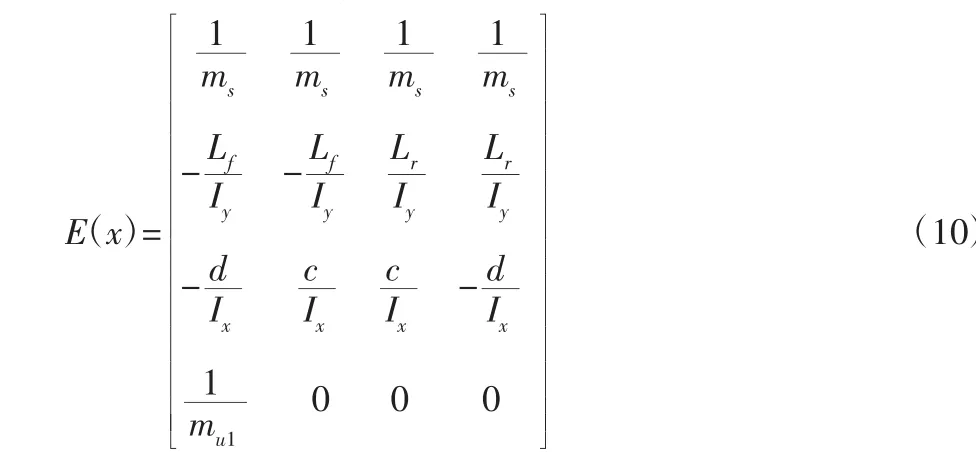
经计算：

detE≠0，LDLfhi（x）=0，（i=1，2，3，4）。根据文献[10]，定义式（9）的反馈控制规律，该反馈形式为：

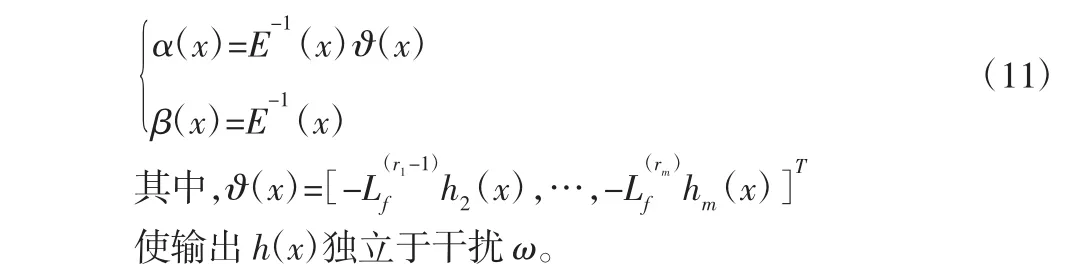
4.3 控制量计算

当系统相对阶r＜n 时，此时原系统不能化为Brnowsky 标准型[11]，但是可以实现系统局部线性化。取微分同胚变换，将系统解耦成4 个独立的互不干扰多的线性子系统，令新的输入变量为：

把式（9）～（12）带入（8）中，将垂向位移加速度等转换为独立的线性二阶系统。通式如下：

根据劳斯判据得，二阶系统稳定的充要条件各项系统的系数都大于0，但系数选取的不同也会直接影响到各个参数的变化。

5 反馈控制二阶系数优化

5.1 目标函数

将四轮路面激励信号作为目标优化的输入信号。式（1）～（7）编写为微分方程组，并作为子m 文件导入到Matlab 中，运用四阶Runge-Kutta 将式（8）方法编写为母m 文件进行调用求解。经计算仿真采用步长h=2.5200e-04。

由于车辆性能指标之间存在的矛盾，为减少车辆行驶过程中悬架振动问题，主要对垂向位移加速度等重要参数进行处理，多目标遗传算法优化目标函数为：

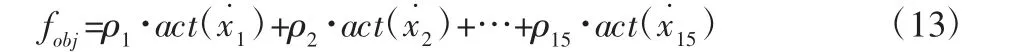
式中：ρi（i=1，…，15）—出参数均方根值的权重值；act（x˙1）—主动悬架系统各状态变量导数均方根值。ρ13=ρ14=ρ15=3，其余权重值默认为1。

根据劳斯判据：系统稳定条件为kij＞0。通过前期仿真处理得出，k 值选取不同会直接影响悬架目标输出参数。设定kij的变化范围为［0 30］。

5.2 优化结果与分析

运用遗传算对目标函数式（13）进行优化求解，优化求解结果，如图4 所示。

图4 输出参数优化结果Fig.4 Output Parameters Optimization Results

由计算结果可知：当迭代次数达到121 次时，种群迭代收敛终止，输出参数总最优均方根值为22.3298。经优化后，kij值分别为：

6 仿真分析

仿真过程中所用到的模型参数，如表1 所示。

表1 仿真所用主要参数Tab.1 Main Parameters Used in Simulation

根据已建立的模型和算法，选择B 级路面，车速设定为20m/s，在Matlab/simulink 中进行仿真对比分析，仿真结果，如图5～图9 所示。

图5 右前悬架动行程对比Fig.5 Comparison of the Right Front Suspension Stroke

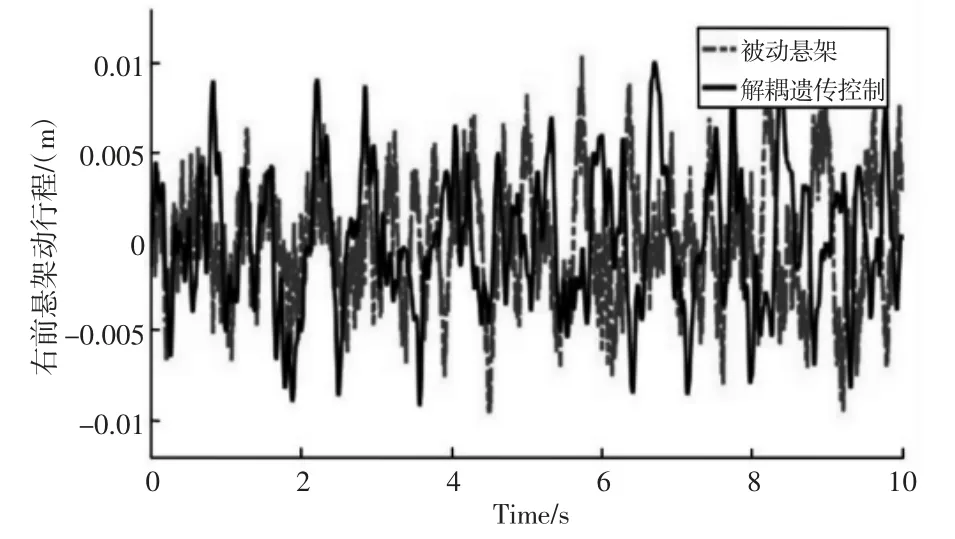
图6 右前轮动位移对比Fig.6 Comparison of Right Front Wheel Movement

图7 侧倾角加速度对比Fig.7 Roll Angle Acceleration Comparison

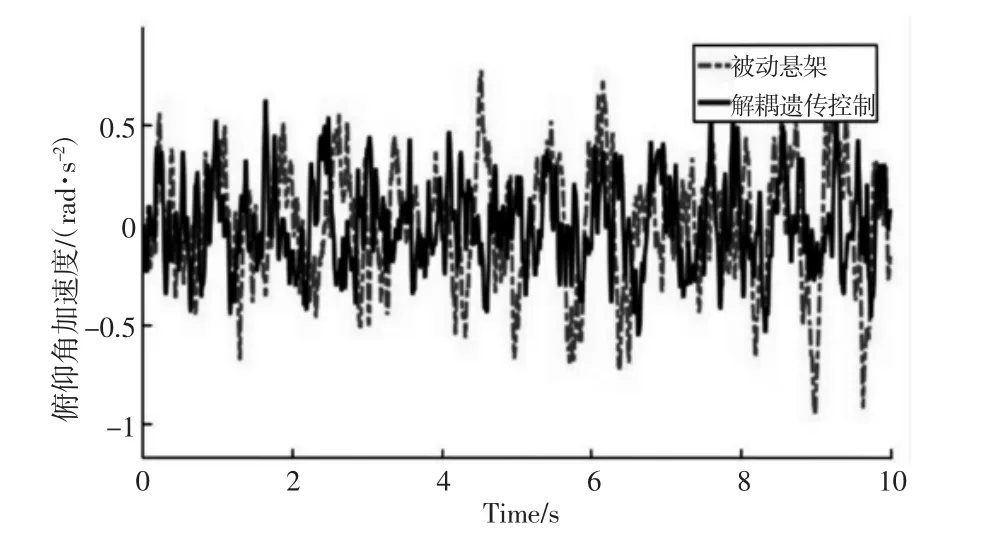
图8 俯仰角加速度对比图Fig.8 Pitch Elevation Acceleration Comparison Chart

限于篇幅原因只列出部分代表性的参数变量仿真对比图。由图5～图9 可以看出悬架的垂向位移、悬架的动行程等都大幅衰减。与被动悬架相比悬架的俯仰角、侧倾角加速度均方根值分别衰减了14%、31.04%；右前悬架动行程均方根值衰减了39.2%；悬架垂向加速度均方根值衰减了10.3%；但是右前轮动挠度均方根值增加了16.36%；产生这种原因是车辆性能指标之间的矛盾，减少悬架动行程的同时一定程度上牺牲了轮胎的动位移，因此要合理的分配悬架系统各项控制指标。

图9 悬架垂向加速度对比Fig.9 Comparison of Vertical Suspension Acceleration

7 结论

（1）建立了整车七自由度侧倾模型和四轮路面激励模型，推导并给出了四轮激励时域模型。（2）针对解耦算法中反馈控制器二阶系数选取的复杂性，运用遗传算法对目标函数进行全局寻优，最后通过Matlab/simulink 进行仿真验证。结果表明：车辆的垂向加速度、俯仰角加速度等指标大幅衰减。