矿用电铲整机运行特性联合仿真研究

穆晓鹏，权 龙，程 珩，李运华

（1.太原理工大学新型传感器与智能控制教育部与山西省重点实验室，山西 太原 030024；2.北京航空航天大学自动化科学与电气工程学院，北京100191）

1 引言

矿用电铲是大型露天矿山的重要挖掘和装载设备，具有生产效率高、可靠性强、工作稳定等优点。挖掘轨迹是确定电铲工作载荷、挖掘过程参数及工作装置优化设计的主要依据，对确定工作装置的几何参数、运动学、动力学等方面研究都具有指导意义[1]。除此之外，电铲在运行过程中载荷变化剧烈，工作装置的疲劳寿命与其载荷特性密切相关。因此，针对电铲挖掘轨迹和载荷特性的研究具有重要的意义。

近年来，国内外学者针对电铲做了很多研究。文献[2]基于挖掘单位物料能耗最低的原则，优化了轨迹控制参数；文献[3]考虑了不同物料倾角和物料面形状对电铲齿尖轨迹控制参数进行了优化，并与传统S 曲线进行了对比分析；文献[4]基于拉格朗日法建立了电铲工作装置的动力学模型，并在Adams 软件中搭建了电铲刚柔耦合虚拟样机模型，分析了工作装置的应力分布情况；文献[5]针对WK-75 型电铲铲斗斗杆组件的疲劳特性进行了研究；文献[6]通过理论分析，结合现场测试，证明电铲挖掘轨迹用对数螺旋线描述是合理的；文献[7]分析了对数螺旋线轨迹的不足，基于机构运动学原理推导了基于推压和提升运动的轨迹方程；文献[8]利用Recurdyn 建立了电铲仿真模型，分析了工作装置的受力情况；文献[9]联合Adams 和Matlab 软件建立了电铲虚拟样机模型，仿真分析了电铲挖掘过程中提升、推压位移、驱动力等关键参数。

上述研究存在以下问题：（1）现有研究中建立的轨迹方程大多是以斗杆的转角与伸出量为自变量，未能在提升速度、推压速度与齿尖轨迹之间建立直观的映射关系，不利于实现轨迹规划与控制，且现有轨迹方程的推导过程忽略了提升电机和推压电机的加减速过程；（2）现有针对电铲的仿真研究多集中在挖掘过程仿真分析，且未能建立电铲整机机电联合仿真模型，无法准确地预测电铲在工作循环中各部分的运行与负载特性。

针对上述问题，首先，考虑了提升电机和推压电机的加减速过程，建立了以时间为历程，由提升速度和推压速度直接决定的挖掘轨迹方程，并分析了斗杆和铲斗的受力情况，确定了切削厚度与挖掘物料体积的计算方法；其次，在多学科仿真软件SimulationX 中搭建了电铲整机机电联合仿真模型；最后，利用所建立的仿真模型，对电铲的整个工作循环过程进行仿真研究，分析电铲工作过程中的运行特性。

2 电铲齿尖轨迹方程的建立

矿用电铲主要由下部行走装置、回转平台和前端工作装置组成，前端工作装置包括动臂、斗杆、铲斗、天轮、鞍座、推压齿轮、吊环等，如图1 所示。其中，提升钢丝绳的一端通过吊环与铲斗连接，另一端绕过天轮，缠绕在车厢内部的提升滚筒上，斗杆的一端通过销轴、拉杆与铲斗连接，另一端通过鞍座与推压齿轮以齿轮齿条的形式连接，动臂下端铰接在回转平台上，其倾角通过调节变幅钢丝绳的长度来调节。

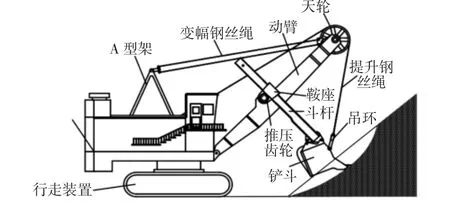
图1 矿用电铲结构简图Fig.1 Mining Shovel Structure Diagram

电铲工作过程中，司机通过控制提升和推压速度的合理匹配使铲斗沿着相应的轨迹挖掘，而提升速度和推压速度均为随时间变化的函数，具有加速-匀速-减速的过程[10]，如图2 所示。

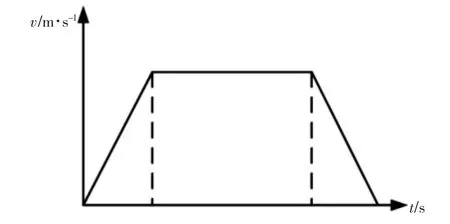
图2 驱动速度曲线Fig.2 Drive Speed Curve

为便于电铲齿尖轨迹的智能化控制与轨迹规划，需要建立以时间为历程，由提升速度与推压速度直接决定的轨迹方程，具体形式为：

式中：X—齿尖的横坐标；Y—齿尖的纵坐标；vQ（t）—提升速度；vtui

（t）—提升速度。

图3 轨迹分析图Fig.3 Trajectory Analysis Diagram

3 电铲工作装置受力分析

3.1 整体分析

电铲在挖掘过程中，斗杆和铲斗是主要的运动与承载部件，且二者之间是固定连接的，因此，以斗杆铲斗组件为研究对象进行受力分析。

C1—斗杆的质心，C2—铲斗的质心，如图4 所示。过C1点作C1M 与DE 垂直并相交于M 点，过C2点作C2N 与DE 垂直并相交于N 点，Fτ和Fn分别为铲斗齿尖受到的切向与法向挖掘阻力，Gdg、Gcd、Gwl—斗杆、铲斗、物料的重力，FQ—提升力，Ftui—推压力，Fz—推压齿轮对斗杆的垂直支撑力，θ6—线段HB 的延长线与提升力FQ的夹角。

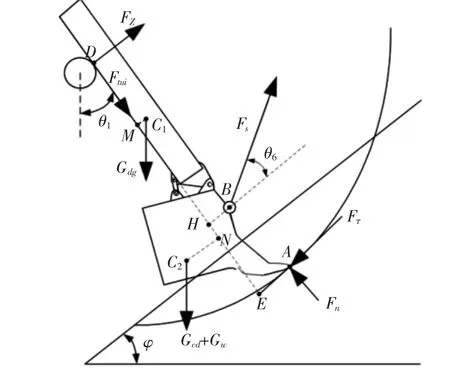
图4 挖掘过程受力分析图

Fig.4 Force Analysis Diagram of Excavation Process根据静力平衡原理，为使斗杆铲斗组件处于平衡状态，斗杆铲斗组件所受外力对瞬时啮合点D 的合力矩为零，即：

3.2 外部载荷的计算

电铲工作装置受到的外部载荷包括齿尖挖掘阻力和斗内物料的重力，为简化运算，采用较成熟的经验公式计算齿尖挖掘阻力，将挖掘阻力分为切向阻力和法向阻力[11]，即：

式中：σw—挖掘阻力比，其值由物料决定；b—铲斗宽度；h—切削层厚度；ψ—比例系数。

切削层厚度h 是指齿尖A 与物料表面的垂直距离，如图5所示。图中：以物料斜面与地面的交点为原点，X 轴水平向右，Y轴竖直向上，此时刻齿尖A 的坐标值为（xi+1，yAi+1），齿尖正上方的物料表面的坐标值为（xi+1，ywi+1），过A 点作AK 与物料斜面垂直并相交与K 点，φ 为物料倾角，β 为φ 的余角。

切削层厚度h（即线段AK 长度）的计算方法为：

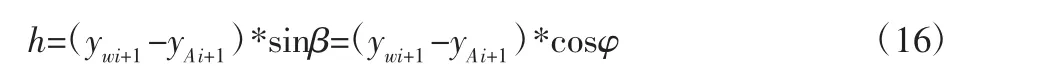
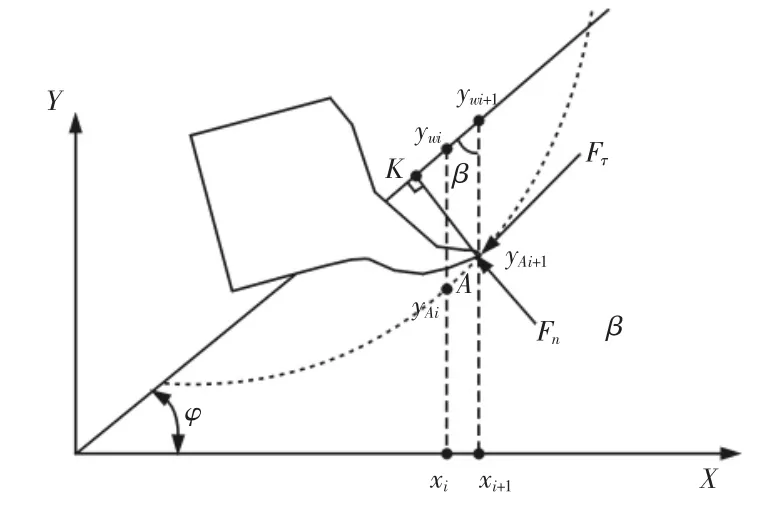
图5 挖掘阻力和物料重力计算示意图Fig.5 The Diagram of Digging Resistanceand Material Gravity Calculation

电铲在挖掘过程中，挖掘的物料不可能全部进入铲斗内部，一部分物料从铲斗两侧流走，因此，铲斗内物料的重力为：

式中：k—实际装入铲斗内的物料体积与挖掘物料体积的比值，一般取（0.9～0.93）[12]；

ρ—物料密度；

S—轨迹曲线在料堆中扫过的截面积；

g—重力加速度。

为计算齿尖轨迹曲线在料堆中扫过的截面积，将电铲的齿尖轨迹进行离散化处理，通过累加小四边形ywi+1ywiyAiyAi+1的面积，如图5 所示。可以求得齿尖在物料中扫过的截面积S，即：

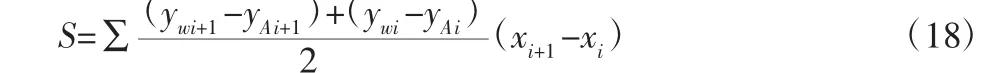
4 建立联合仿真模型

以某型号电铲为研究对象，根据电铲的工作原理，采用SimulationX 软件构建，如图6 所示。能基本反应电铲工作状况的机电联合仿真模型进行仿真研究，其中，利用SimulationX 软件的带传动模块建立提升钢丝绳与绷绳模型，既能体现了钢丝绳的柔性特点，也保证了仿真效率；利用SimulationX 的电-机械模块与信号模块建立各变频电机及其控制系统仿真模型。

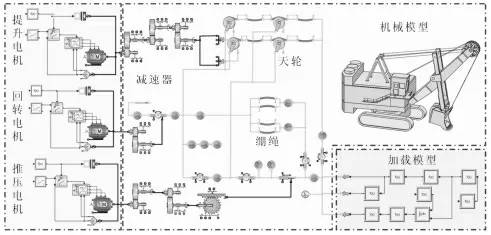
图6 电铲机电联合仿真模型Fig.6 Mechanical and Electrical Co-Simulation Model of Electric Shovel

根据前文所述，电铲承受的外部载荷包括挖掘阻力与物料重力，且均与齿尖运行轨迹相关。为此，在仿真模型的铲斗齿尖处设置位移传感器，得到齿尖与物料表面的坐标信息，并按照前文所述的载荷计算方法，将挖掘阻力与斗内物料重力施加到虚拟样机上，所施加的外部负载曲线，如图7 所示。

图7 外部负载曲线图Fig.7 External Load Curve

5 电铲工作循环仿真分析

参考某电铲工作现场的实测数据，确定仿真工作循环时间为44s，其中挖掘过程为（0～13.4）s，上车回转过程为（14～23）s，卸载过程为（23.5～31.5）s，回转返回过程为（32～44）s。

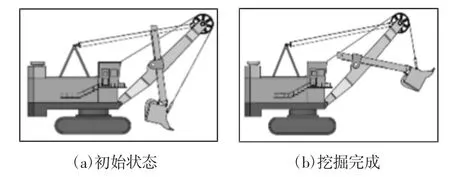
仿真过程中电铲挖掘-回转-卸载-下降及回转复位作业过程，如图8 所示。其中，图8（a）～图8（f）分别为：初始位置、挖掘完成、上车回转、开斗卸载、返回初始位置的部分截图。电机转速曲线，如图9 所示。由图可知，在挖掘过程，提升电机最大转速为471r/min，推压电机最大转速为136r/min；上车回转阶段，提升电机和推压电机停止转动，回转电机驱动上车转动；在卸载阶段，提升、推压、回转电机均停止转动，开斗装置打开使斗内物料卸载；回转返回阶段，提升、推压、回转电机协同工作，使电铲工作装置回到挖掘初始状态。

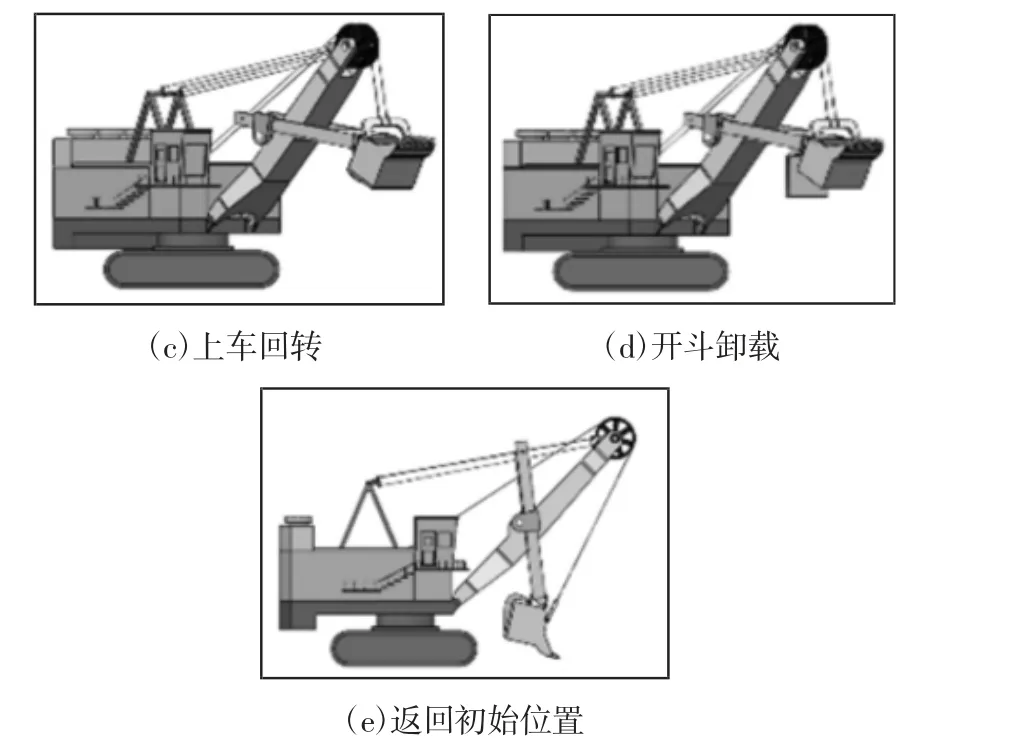
图8 整机循环动作仿真Fig.8 Simulation of Whole Machine Circulation

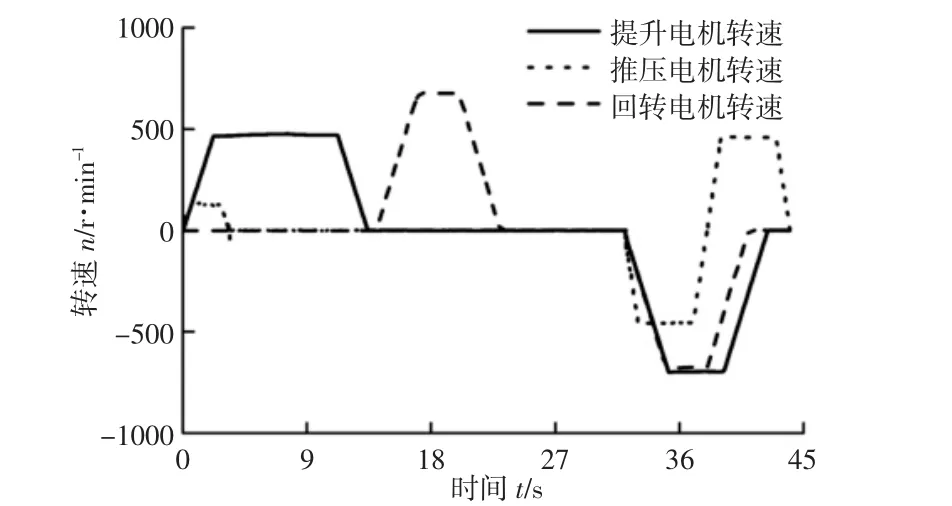
图9 电机转速Fig.9 Rotation Speed of Electric Motor

斗杆转速和转角曲线，如图10 所示。由图可知，在挖掘过程，斗杆最大转速为8.6deg/s，最大转角为78.5°，在上车回转-开斗卸载阶段，斗杆基本不转动，在回转返回阶段，斗杆首先反向转动到最低位，然后再正向调整到初始位置附近，这与实际电铲挖掘过程中的运动特性基本吻合。提升力和推压力曲线，如图11 所示。由图可知，在电铲工作过程中，提升力和推压力的变化趋势基本相同，提升力最大值为877kN，推压力最大值为394kN，均出现3.5s 左右（此时切削厚度最大）。在上车回转过程中，提升力和推压力基本不变；在卸载过程中，提升力减小，推压力基本不变，这是因为随着斗内物料的减少，维持电铲工作装置平衡所需要的提升力变小，而斗杆处于水平状态，推压力对维持工作装置平衡不起作用，所以在卸载过程中推压力变化不大。

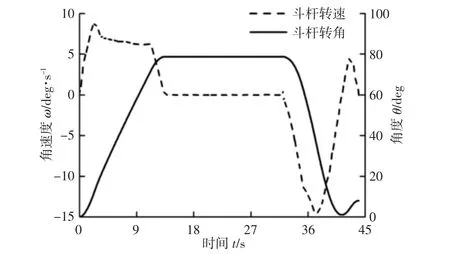
图10 斗杆转速与转角Fig.10 Rotation Speed and Angle of Dipper Handle

图11 提升力和推压力Fig.11 Force of Lifting and Crowding

提升电机功率与提升位移曲线，如图12 所示。由图可知，提升电机输出功率最大为550kW，满足电机功率要求。经过计算图中曲线包络面积可知，在挖掘过程中，提升电机对外做功3794kJ，消耗电能4384 kJ，电动效率为86.5%。在上车回转和物料卸载过程，提升电机输出轴由机械抱闸抱死，功率为零。在回转返回过程，斗杆和铲斗因自重下降，提升电机功率为负，斗杆和铲斗的重力对提升电机做功785kJ，可发出电能652kJ，发电效率为83.1%。

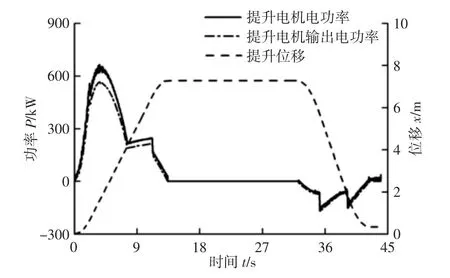
图12 提升电机功率与提升位移Fig.12 Power of Lifting Electric Motor and Displacement of Lifting

推压电机功率与推压位移曲线，如图13 所示。由图可知，推压电机功率在挖掘开始阶段为负，这是因为挖掘开始阶段推压力和推压位移方向相反。随着齿尖挖掘阻力的增大，推压力与推压位移方向相同，推压电机的功率由负变为正，3.5s 之后推压功率为零，推压位移最大为0.3m，此后推压电机因机械抱闸装置抱死，推压功率为零。在回转返回阶段，为保证工作装置下降时不与物料表面碰撞，需先缩回斗杆（推压电机对斗杆做功），待斗杆与地面接近垂直时再伸出（斗杆和铲斗的重力对推压电机做功），因此在这个阶段，推压位移和推压电机的功率均经历由正变为负值的过程。回转电机功率与上车回转角度曲线，如图14 所示。由图可知，在上车回转阶段，回转电机的输出功率最大为261kW，满足电机功率要求，上部平台的回转角度最大为90°。其中，在加速时，回转电机功率为正，制动时，回转电机功率为负。在回转返回阶段，回转电机功率的变化趋势与上车回转阶段基本相同，最大输出功率为247kW，较上车回转阶段偏小，这是因为在回转返回阶段，斗内物料为零，且伴随着斗杆和铲斗下降的过程，上车部分等效转动惯量较上车回转阶段变小。

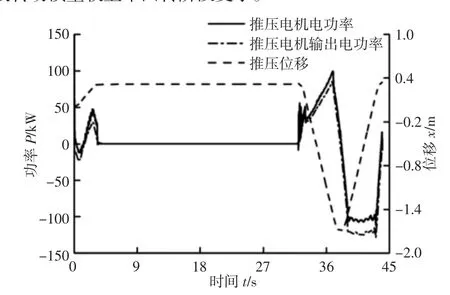
图13 推压电机功率及推压位移Fig.13 Power of Crowding Electric Motor and Displacement of Crowding

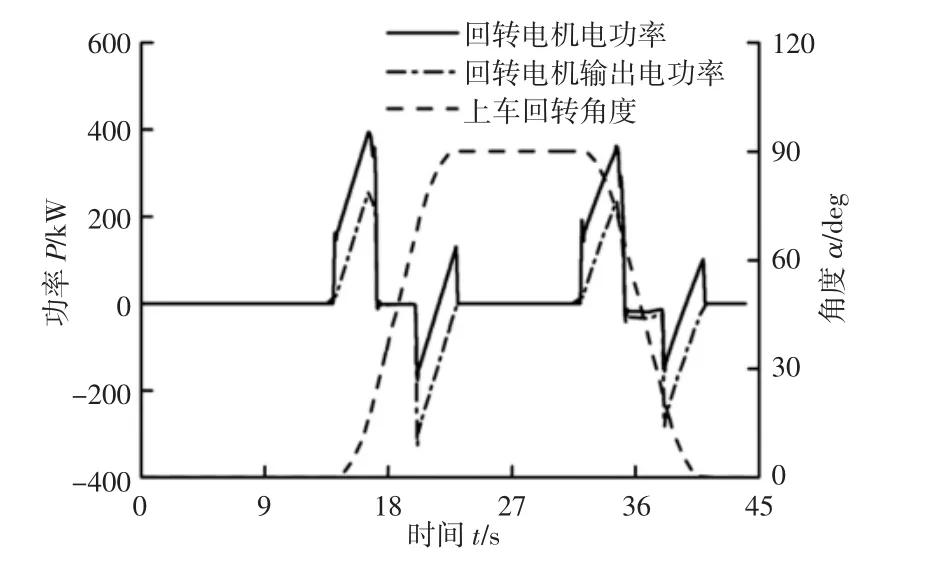
图14 回转电机功率和上车回转角度Fig.14 Power of Rotary Electric Motor and Rotation Angle of Upper Body

6 结论

（1）考虑提升电机和推压电机的加减速过程，建立了以时间为历程，由提升速度和推压速度直接决定的齿尖轨迹方程，并分析了电铲斗杆和铲斗的受力情况，确定了切削层厚度与挖掘物料体积的计算方法，为电铲的智能化控制与最优轨迹规划奠定了基础。

（2）利用电铲整机机电联合仿真模型对电铲工作循环过程的运行特性进行仿真研究，仿真结果表明：在挖掘过程中，提升电机输出功率为正值，最大输出功率为550kW，电机效率为86.5%，推压电机功率经历了由负变为正的过程；在上车回转阶段，提升电机和推压电机功率均为零，回转电机在回转加速时功率为正，最大输出功率为261kW，在回转减速时功率为负；在回转返回阶段，提升电机发电效率为83.1%，推压电机功率经历了由正变为负的过程，回转电机的功率变化趋势与上车回转阶段相同，但最大功率值偏小。