基于铁路客运运营条件信息的 径路算法研究

刘文韬，牛青坡，李天翼，宋 阳

（中国铁道科学研究院集团有限公司 电子计算技术研究所，北京 100081)

0 引言

截至2020年12月底，我国铁路运营里程达14.63万km，规模居世界第二，其中高速铁路里程3.8万km，占世界高速铁路总里程近70%，多年稳居世界第一。“四横四纵”高速铁路网络已经建成，“八横八纵”的高速铁路网络正在逐步建设，在京津冀、长三角、珠三角等经济发达和人口稠密地区的城际网络日益完善。《新时代交通强国铁路先行规划纲要》提出，到2035年，全国铁路运营里程达20万km左右，高速铁路达7万km左右，铁路网内外互联互通、区际多路畅通、省会高效连通、地市快速通达、县域基本覆盖、枢纽衔接顺畅。铁路快速发展在便利旅客出行的同时，也对铁路客运运营管理工作提出了更高的要求。

铁路客运运营条件是指铁路线路、车站组织旅客运输生产活动的营业办理条件，主要业务类型包括：线路开通、车站命名(更名)、车站开办、停办或变更客运业务等，是铁路业务部门管理路网信息的重要工作。长期以来铁路客运运营条件信息管理采用人工管理为主、简单电子化表格为辅的管理模式。伴随铁路网规模扩大，结构日益复杂，现有管理模式已不能与管理需求相匹配，亟需实现铁路客运运营条件的信息化管理，提高铁路客运运营条件管理的效率和水平。

查找计算2个车站之间的合理可达径路及里程，是铁路客运运营条件管理的日常工作，以铁路客运运营条件信息为基础，研究经典图论中的径路算法[1]，构建指定起始站、终到站条件下可达径路的搜索模型，改变依赖人工经验或纸质地图查找计算的工作模式，为铁路客运运营条件管理人员提供高效实用的信息化工具[2]。

1 径路搜索算法适应性分析

通过分析比对，在诸多图论径路搜索算法中，选取深度优先搜索算法(DFS算法)、狄克斯特拉算法(Dijkstra算法)和A*(A-Star)算法进行重点研究，用Java语言实现算法，在相同的数据基础上进行模拟验证，并结合需求特点对不同算法进行适用性分析。

1.1 DFS算法

DFS算法用于遍历或搜索树和图，其基本思路是从图中1个节点出发，每次遍历当前访问节点的1个相邻可达节点，一直到访问的节点没有未被访问过的相邻可达节点为止。然后采用依次回退的方式，查看遍历路径上的每一个节点是否有其他未被访问的相邻可达节点[3]。上述访问过程完成后，全部连通图中的所有节点都已经遍历完成，通过此算法可以搜索指定2点间所有可达径路。DFS算法是一个不断遍历回溯的过程，采用了递归的思想实现搜索目标结果集。

1.2 Dijkstra算法

Dijkstra算法是由荷兰计算机科学家狄克斯特拉于1959 年提出的，是经典最短径路算法之一，是能够获取图中的指定节点到其余各节点的单源最短径路算法[4]，其核心思想是以起点为中心向外层扩展，求出该节点到其他节点的最短路径，即从 1个点开始到其他所有点的路径[5]。Dijkstra算法应用贪心算法的策略[6]，每次遍历到指定节点距离最近且未访问过的顶点的邻接节点，直到扩展到终点为止。

1.3 A*算法

A*算法又称A-Star算法，是基于启发式的最短径路算法，每次利用一个确定的评价函数对所有没展开的节点进行评价，从而找到最符合评价标准的节点[7]。A*算法中的距离估算值与实际值越接近，最终搜索速度越快，通常用曼哈顿距离作为评价函数预估距离代价，搜索过程取决于A*算法采用的评价函数，搜索效率受限[8]。

1.4 算法比对

为综合分析不同算法的适用性，采用构建静态站点模型方式进行执行情况分析，节点模型示意图如图1所示。图1中圆圈代表节点，圆圈中的字母代表节点名称，数字代表节点序号，圆圈之间的线段表示节点之间存在可达径路，径路旁边的数字代表径路长度。用Java语言实现上述3种算法，验证内容为：①求A点到U点的最短径路及其距离；②求A点到U点的所有可达径路；③计算算法的执行时间。3种算法对比结果如表1所示。

通过对DFS算法、Dijkstra算法、A*算法特点和执行结果的分析可知，Dijkstra算法是一种寻找单源到其他所有节点的最短路径搜索算法，需要指定起点，可以计算出起点到图中其他所有可达点的最短路径；A*算法是一种寻找指定2点间最短路径的算法，搜索过程取决于A*算法采用的评价函数；DFS算法在问题求解过程中对图进行遍历，能够搜索指定2点间所有可达路径的算法，适用铁路客运运营条件信息中求解给定始发、终到站之间所有可达路径的需求。虽然利用静态站点计算DFS算法在开发环境下优化前的指标并不是最优，综合分析业务应用场景，该算法符合铁路客运运营条件业务管理需求，因而选择DFS算法作为铁路客运运营条件径路搜索算法的基础。

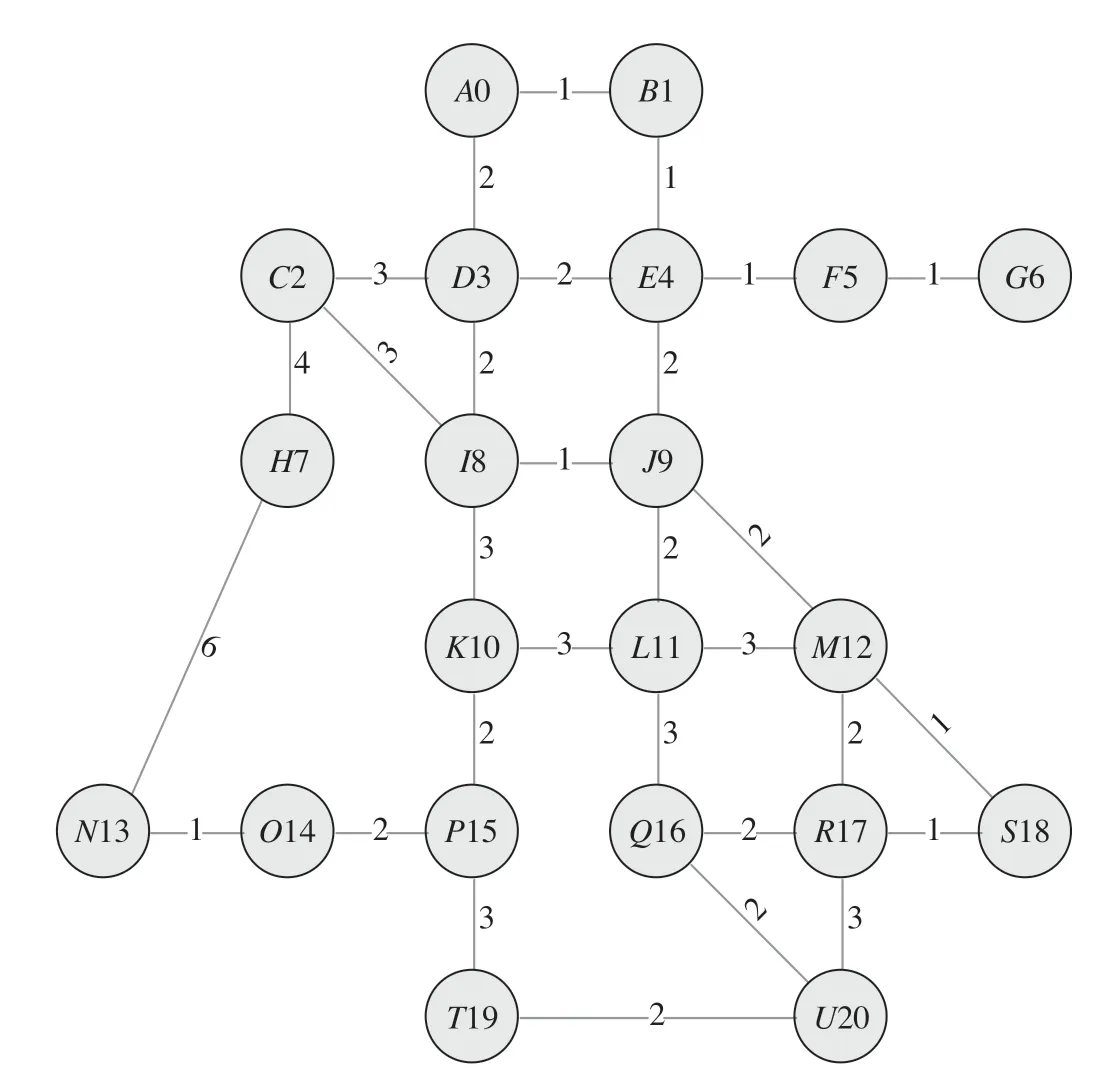
图1 节点模型示意图Fig.1 Diagram of node model

表1 3种算法对比结果表Tab.1 Comparison among three algorithms

2 基于铁路客运运营条件信息的径路算法

将Java实现DFS算法应用于经过规范化整理的铁路客运运营条件数据后，由于车站众多、线路之间交叉关系复杂等原因，导致算法递归调用层次过多，搜索出大量不合理的绕行径路，时间开销剧增，在实际业务中不可用。因此，应基于铁路客运运营条件信息特点，从简化搜索节点、限定搜索区域、结合列车开行、控制递归深度等方面对DFS算法进行优化，以提升计算效率。

2.1 简化搜索节点

铁路客运运营条件信息中办理客运业务、乘降所、结算站等各类车站近5 000个，全部车站都作为路网图模型节点，将大大增加算法的搜索深度，消耗大量内存和计算资源，严重影响径路搜索效率。依据铁路客运运营条件信息中线路、车站及线站关系等特点，选取有2条及以上线路经过的结算站作为构建递归搜索的基本节点，再结合始发、经由和终到车站信息，形成完整的径路搜索图。经上述优化筛选后，搜索节点数量得到有效控制，数量降为800个左右，不到全部车站的1/6，算法占用资源降低，搜索效率有了较大的提升。

算法实现将铁路网定义为图G= (V，E)，V是图G中各节点车站集合，V= {vi|i= 1，2，…，n}，其中vi代表第i个车站，vi= {(xi，yi) |i= 1，2，…，n}，n为车站的数量，其中xi为vi车站的经度，yi为vi车站的纬度；E为连接站点的线路作为图中的边，其值为线路端点站间的里程，E= {(u，v) |u，v∈V} = {e1，e2，…，ej，…，em}，其中ej代表第j条线路，m为线路的条数。

结算站优化前后节点示意图如图2所示。优化前包含全路范围车站，其中辽宁朝阳、沙城、忻州、杨村等站并不是结算站，去除这些车站不影响路网的通达性，通过筛选结算站方式可以大量减少节点数量。

2.2 限定搜索区域

由于路网结构复杂，在始发、终到站之间存在多条可达径路，其中有些径路会有较大的绕行现象，此部分搜索结果除了通达性之外，没有实际应用意义，应予以舍弃，进一步降低无效搜索数量，提升算法效率。

算法改进应结合始发站、终到站的实际情况对搜索区域进行限定，以始发站、终到站的经纬度信息为基础，按照始发站、终到站所在经纬度位置，设置一定范围内的经纬度偏移量阀值(如1°，2°等)，确定新的始发、终到位置，以两者之间的连线做对角线确定四边形的搜索区域，在区域内的车站为合理搜索的节点。经纬度偏移量系数设置为p1= {z|z= 1，2，…，5}。其中z代表偏移度。通过搜索区域限定，算法的搜索范围大为降低，既能节省无效搜索的开销，又能搜索出合理的径路。

以北京到广州为例，优化前后的限定搜索区域变化如图3所示，将偏离北京和广州较远的沈阳、长春、哈尔滨、通辽、西安、青岛和上海等方向的线路车站做了有效的排除。

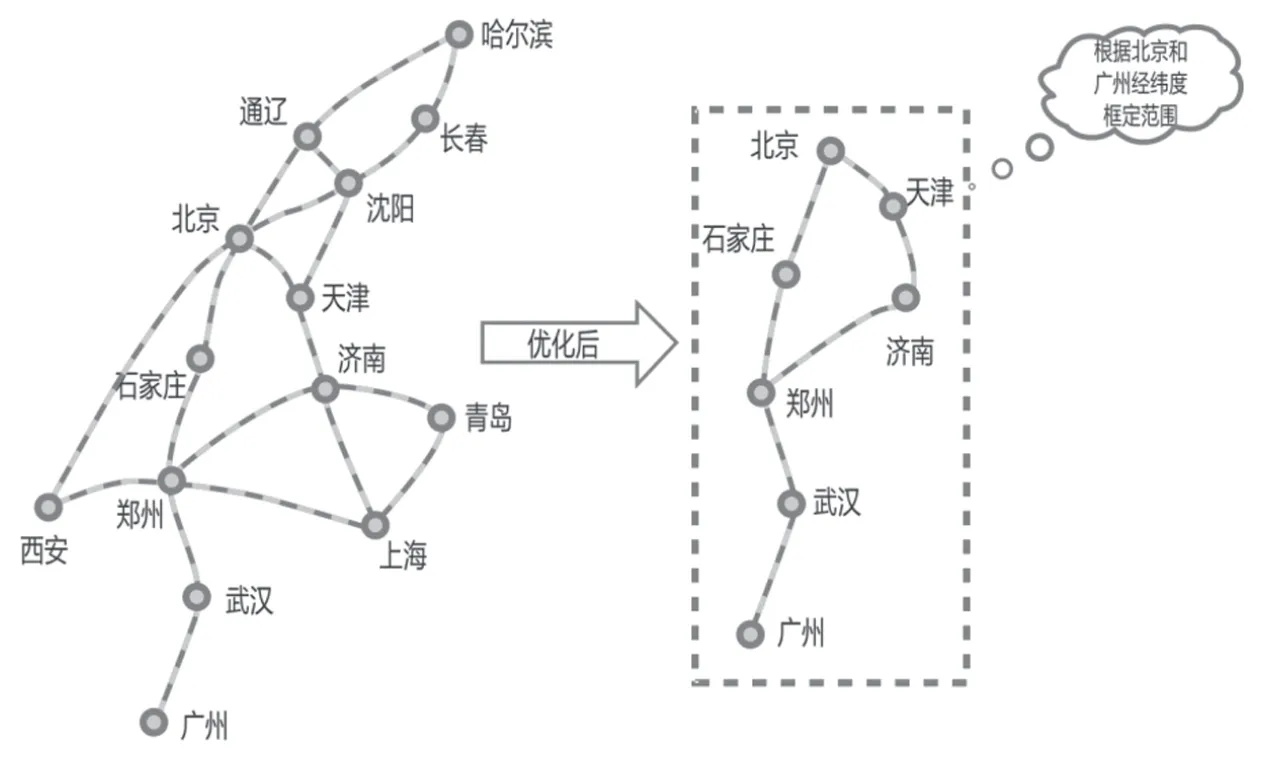
图3 优化前后的限定搜索区域变化Fig.3 Change in limited search area before and after optimization

2.3 结合列车开行

算法模型中按照路网基本信息进行关联，会形成较为复杂的网络结构，存在较多不合理的可达径路。为进一步提升可达径路的合理性，搜索过程中与实际列车运行情况相结合，加入列车径路因素，将有效开行列车运行线路作为径路搜索的重要依据，简化节点间的连接关系，缩小搜索范围，提升算法效率。

列车开行径路因素由p2表示，p2=φ(A，B)，A∈VK，B∈EK，其中A代表变线站因素；VK代表列车运行径路中变线站集合；B代表径路因素；EK是列车运行径路中行经线路集合。

以北京到广州的径路为例，结合列车开行优化后搜索径路简化示意图如图4所示。将北京至广州区间不会行经的北京—张家口—原平—太原、北京—天津—济南—郑州、郑州—十堰—襄阳—黔江—长沙南等绕行区间排除。

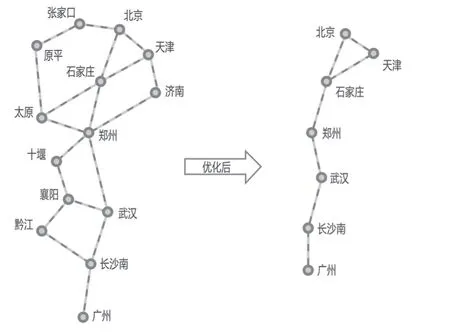
图4 列车开行优化后搜索径路简化示意图Fig.4 Simplified diagram of search paths optimized by train plans

2.4 控制递归深度

为使算法的时间效率可控，对递归条件进行优化，采用递归深度和累计里程2种机制控制算法是否结束，结合对铁路客运运营条件信息的综合分析，设置递归深度阀值及最大累计里程阀值，超过阀值的径路视为不合理径路，有效控制算法递归深度，确保时间效率。

用T代表节点深度控制阀值，超过阀值的搜索将被终止。X代表里程控制阀值，第一条径路计算完成后的里程阀值X1依据首次计算得到的径路里程S(p1)和经纬度偏移量p1系数计算得到

式中：X1为第一条径路计算完成后的里程阀值；Z1为2个站间连线与低经度站纬线间形成的角度；X ′为校对里程，设置范围为业务可接受的里程偏差，验证中取X ′∈[0，50]。依次按照最短里程进行阀值修正，则当前径路里程可以表示为

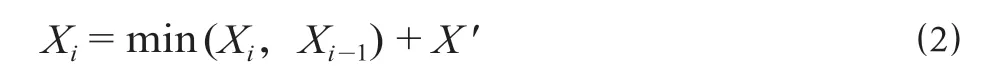
式中：Xi为当前径路里程；Xi-1为前序径路里程。

3 基于铁路客运运营条件信息的径路算法优化流程及效果

3.1 算法优化流程

基于铁路客运运营条件信息的径路算法优化以保留核心关键节点、降低铁路客运运营条件信息复杂度为基础，通过简化搜索节点、经纬度限定搜索范围、结合列车开行、设置递归深度和里程阀值等优化，有效提升求解效率，得到符合业务需求的最优径路。经过优化后的基于铁路客运运营条件信息的径路算法搜索可达径路时，在铁路客运运营条件路网信息中指定始发站vs经由vv站至终到站ve的最优可达径路里程表示为

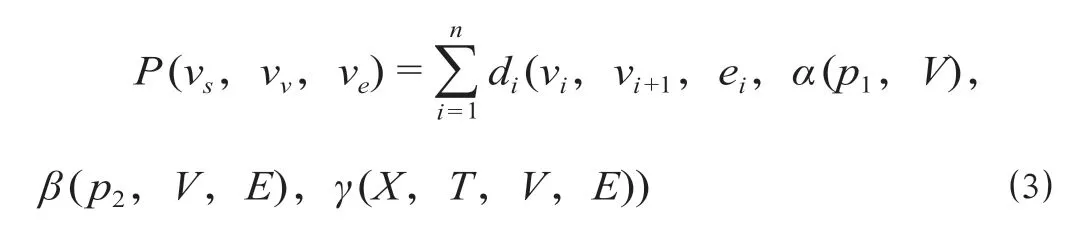
式中：vs代表始发站；vv代表经由站；ve代表终到站；ei代表vi站到vi+1站的最优径路；α(p1，V)为按照结算站及经纬度偏移量筛选的节点集合；β(p2，V，E)为按照列车开行径路优化后的车站及站间可达线路关系；γ(X，T，V，E)为按照节点深度及里程进行的线站搜索控制范围；di为vi，vi+1之间经过α，β，γ综合判定后的优选径路里程。

基于铁路客运运营条件信息的径路算法优化流程如图5所示。

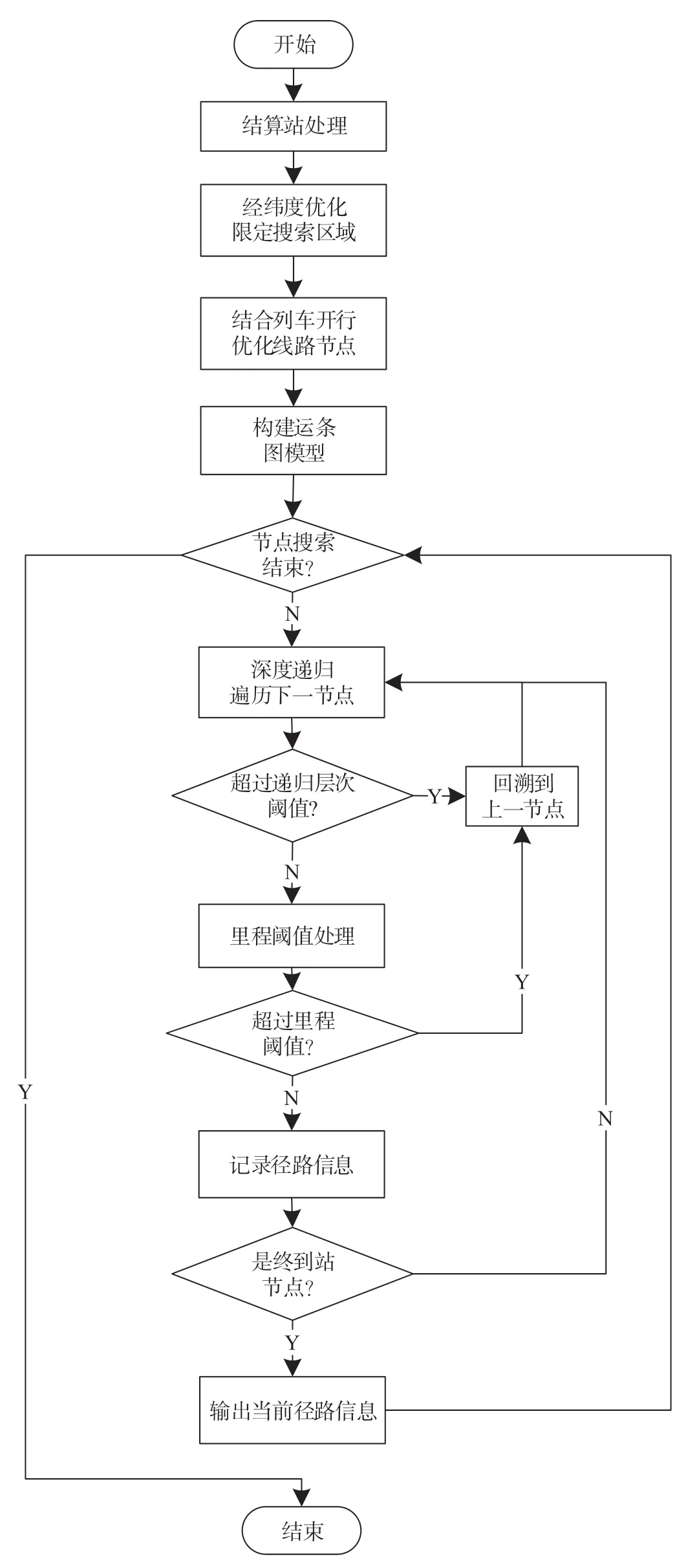
图5 算法优化流程图Fig.5 Flow chart of algorithm optimization

3.2 算法优化效果

以北京—广州区间为例，优化之前全部线站加载至模型中参与经由运算，结果集中会出现与始发站、终到站偏离较远的车站节点，经过线路、车站节点较多，未进行递归深度控制，不仅运算时间长，执行结果产生了大量不合理的径路。优化前后径路如图6所示。

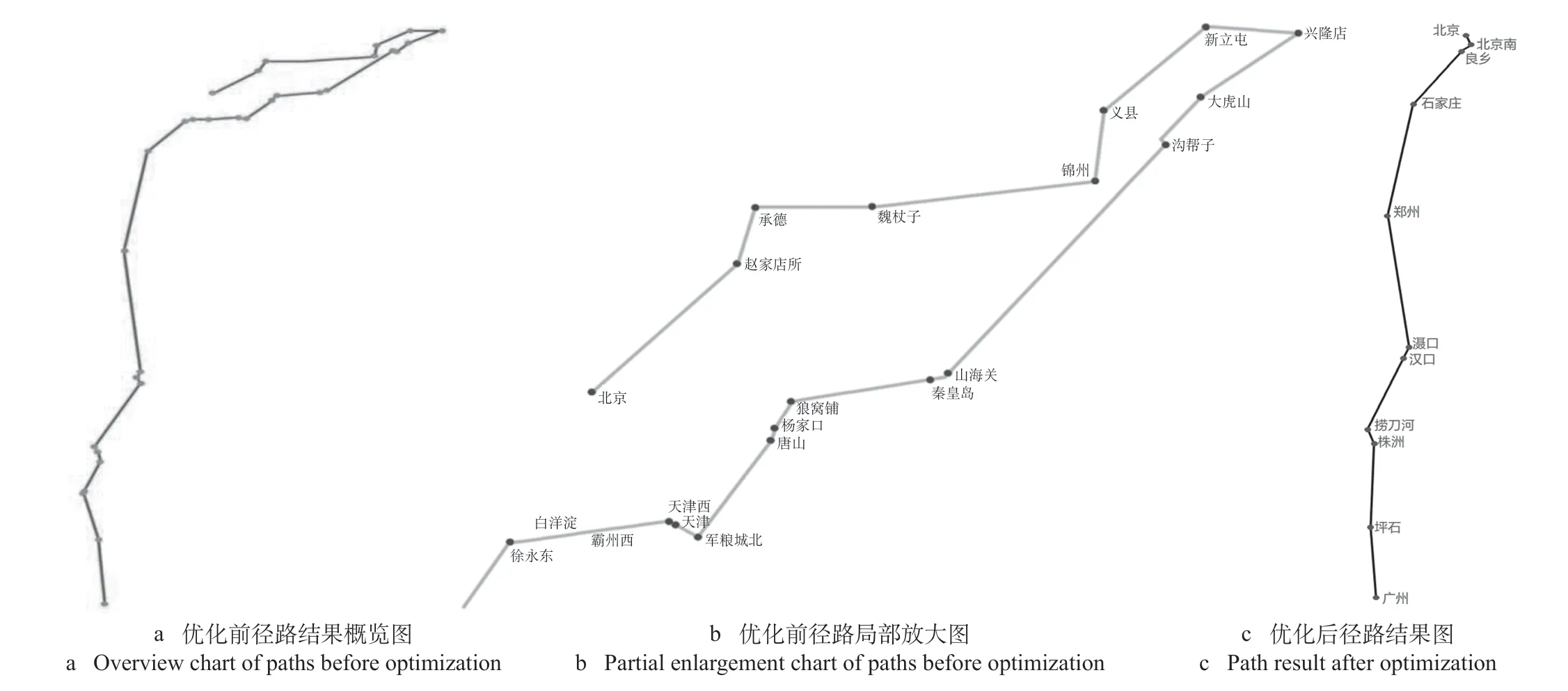
图6 优化前后径路图Fig.6 Path charts before and after optimization

算法优化前后的效果对比如表2所示。

表2 算法优化前后的效果对比Tab.2 Comparison between optimization algorithms

经过节点、经纬度、列车开行、递归深度的优化后，节点规模大幅度减少，排除了偏离始发站、终到站较远的径路，不会绕行距离较远的车站，会与列车开行紧密结合，径路合理性明显优于原始算法，与实际业务要求相符，同时时间效率有较大提升，算法用时由百秒级降至毫秒级。

4 结束语

在我国铁路路网建设规模逐步扩大，结构日益复杂的情况下，围绕路网信息的业务特点，对线路、车站进行关联，设计路网模型，以DFS算法为基础进行研究改进，能够解决搜索深度过大情况下的合理径路高效求解难题，快速全面地搜索出符合业务需求的站间合理径路，有效提升铁路客运运营条件的信息化管理水平。未来可根据实际应用情况综合考虑客流分布、旅客偏好等因素对模型进一步优化，为旅客互联化、智慧化的美好出行服务提供技术支撑，为网状综合交通的互联互通管理提供新的思路。