基于PSR模型及博弈组合赋权的 城市轨道交通运营水平评价研究

薛 亮，赵胜川

（大连理工大学 交通运输学院，辽宁 大连 116024)

0 引言

近年来，我国城市轨道交通行业迎来快速发展期，根据交通运输部统计数据，截至2020年底，我国开通运营轨道交通的城市达44个，运营里程达到7 545 km，运营线路总计233条，车站4 660座。 随着城市轨道交通的快速发展，运营线网不断扩大，虽然其运营水平不断提高，但各个运营企业的发展状态不尽相同。为更好地对城市轨道交通运营系统进行评价，交通运输部、中国城市轨道交通协会、中国交通运输协会城市轨道交通专业委员会分别建立了运营评价指标体系，意在掌握和对比各城市轨道交通运营企业运营系统发展状态。一些专家学者通过构建评价指标体系对系统的运营水平进行综合评价。梁仁鸿等[1]选取16项指标构建综合交通发展评价指标体系，并对综合交通总体发展水平进行分析；周健等[2]选取5个货运基础指标和4个客运基础指标，采用Fisher-ideal方法集成基础指标对中国运输服务水平进行评价；张广厚等[3]从安全性、经济性、舒适性等3个方面选取指标，构建了基于仿真方法的综合交通枢纽动态运营水平评价指标体系；Aalok等[4]提出了一个含有4个驱动因素、16个维度和74个属性的社会可持续性评价指标体系，用以对货运系统运营水平进行评价；马驷等[5]通过构建高速铁路运输供给服务水平指标体系，运用灰色综合评价法，对高速铁路运输供给运营服务水平进行评价。Madhu等[6]从经济、社会和环境3个领域选取12个指标构建可持续性整合评价指标体系来确定地铁与公交之间的融合程度。通过文献分析，通过构建评价指标体系对交通系统进行宏观及微观评价的研究成果较为显著，可以借鉴于城市轨道交通运营水平评价研究。

因此，为解决量化评价城市轨道交通运营系统发展状态的问题，在专家学者研究的基础上，运用PSR模型原理建立城市轨道交通运营系统评价关键指标体系，采用主观赋权和客观赋权相结合的方法，引入博弈论思想对关键指标进行组合赋权，进而构建城市轨道交通运营水平评价模型，对处于不同发展阶段的城市轨道交通运营状态进行评价。

1 城市轨道交通运营指标体系构建

1.1 基于PSR模型的城市轨道交通运营系统机理

压力-状态-响应(Pressure-State-Response，PSR)模型是统计学中的一个经典模型，PSR模型能从系统的角度，全面分析系统发展变化所面临的压力、所处的状态及所采取的响应，并动态地反映其因果关系和作用机理，为进一步的发展激励和约束提供参考借鉴。城市轨道交通运输的“产品”是乘客服务，对于运营系统来说，其“压力”归根结底是来自于乘客的需求强度，如运营系统中客运量、拥挤度、客运强度等指标，给运营系统带来一定“压力”。城市轨道交通运营系统要缓解乘客带来的“压力”，可通过改变基础设施及行车运行指标做出“响应”，如增加运营长度、车站总数、配属车辆数，缩小最小发车间隔等措施来“响应”乘客需求带来的压力。城市轨道交通运营系统的运行“状态”可以用能耗与成本来体现，如运营票务收入、每人次成本等指标可以反映客运“压力”在系统中的运行“状态”，运营总成本、牵引总能耗等可以反映基础运行系统的运行“状态”。客运服务、基础运行、能耗成本这3个维度，总体上反映了城市轨道交通运营系统在PSR逻辑框架下的压力、响应、状态互动关系与作用机理。基于此，构建城市轨道交通运营PSR模型如图1所示。

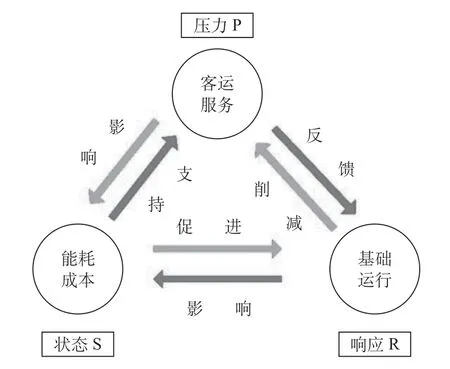
图1 城市轨道交通运营PSR模型Fig.1 PSR model of urban transit operation

1.2 指标体系构建

基于城市轨道交通运营PSR模型及其作用机理，在构建指标体系时，考虑到指标的高辨识度、多层次性和数据的可获取性，将指标选择定位在客运服务、基础运行、能耗成本3种因素中，以中国交通运输协会城市轨道交通专业委员会建立的《城市轨道交通运营绩效评估体系(MOPES)》为基础，该指标体系包含一级指标4个，二级指标84个，包含了网络层面、线路层面的运营数据。研究指标参考MOPES指标体系，从整个运营系统的角度，选取网络层面的指标为研究基础数据，不考虑单个线路层面的运营情况，同时删除了如网络运营长度增长率等线性相关性较强的指标。根据城市轨道交通运营PSR模型，从压力-状态-响应3个方面，构建目标、准则、指标3个层次的运营指标体系。城市轨道交通运营指标体系如表1 所示。

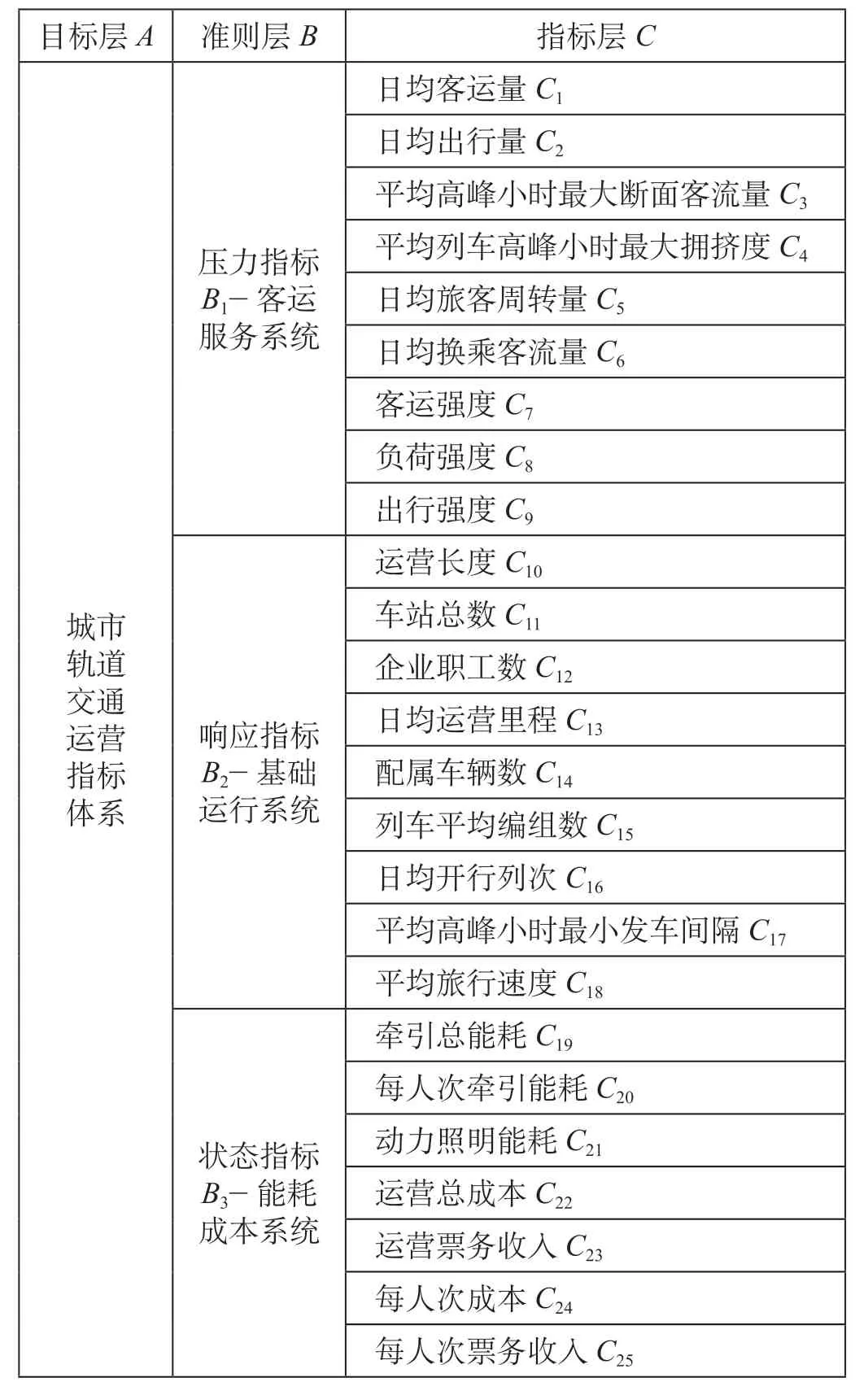
表1 城市轨道交通运营指标体系Tab.1 Index system of urban transit operation

2 城市轨道交通运营水平评价模型

城市轨道交通运营水平评价模型由多项反映城市轨道交通运营状况的关键指标构成，既可以量化、直观地反映城市轨道交通运营水平，也可以对城市轨道交通运营水平进行监测和度量。通过剖析运营水平评价模型，可挖掘反映城市轨道交通运营发展形态的特征。

2.1 博弈论组合赋权法权重确定

指标权重的确定方法依照其特征可分为两大类：主观赋权法和客观赋权法[7]。在遵循有效性、合理性、科学性、目的性、联系性等原则和要求的前提下，同时具有主观赋权法的“功能驱动”思想和客观赋权法的“差异驱动”思想，研究基于博弈论思想将2种赋权法所得的权重进行融合，得到指标的组合权重。基本步骤如下。

2.1.1 主观赋权法权重确定

研究选择主观赋权法中的层次分析法(Analytic Hierarchy Process，AHP)来进行权重计算，AHP评价尺度表如表2所示。AHP计算思路是：①根据评价尺度表，构造各层次判断矩阵A= (aij)n×n，将A矩阵中的元素按列归一化后的同一行元素相加除以n，其对应的向量w= (w1，w2，…，wn)T即为各指标要素的权重向量。②设为为n阶正负反矩阵A的最大特征根，判断矩阵A的一致性指标为。③设一致性比例当CR= 0时，A为完全一致性矩阵；当CR＜0.1时，A为满意一致性矩阵，即通过一致性检验。④最底层各元素对最高层(目标层)重要性的排序权重进行一致性检验，即RI=其中wi为准则层对目标层的权重，CIi，RIi为指标层对准则层的CI和RI。随机一致性指标RI具体值如表3所示。

2.1.2 客观赋权法权重确定

研究选择客观赋权法中的熵值法进行权重计算，其基本思路是：设有m个样本、n项指标，为了消除评价指标的数量级、单位、量纲不同而对评价结果带来的影响，首先采用钱吴永等[8]提出的均值化算子法进行无量纲处理，再对无量纲处理后的元素计算第j(j= 1，2，…，n)项指标下，第i(i= 1，2，…，m)个评价对象的特征比重pij=计算第j项指标的熵值如果xij对于给定的j都相等，可得ej=emax= 1；定义差异系数为gj= 1 -ej，确 定指标权重

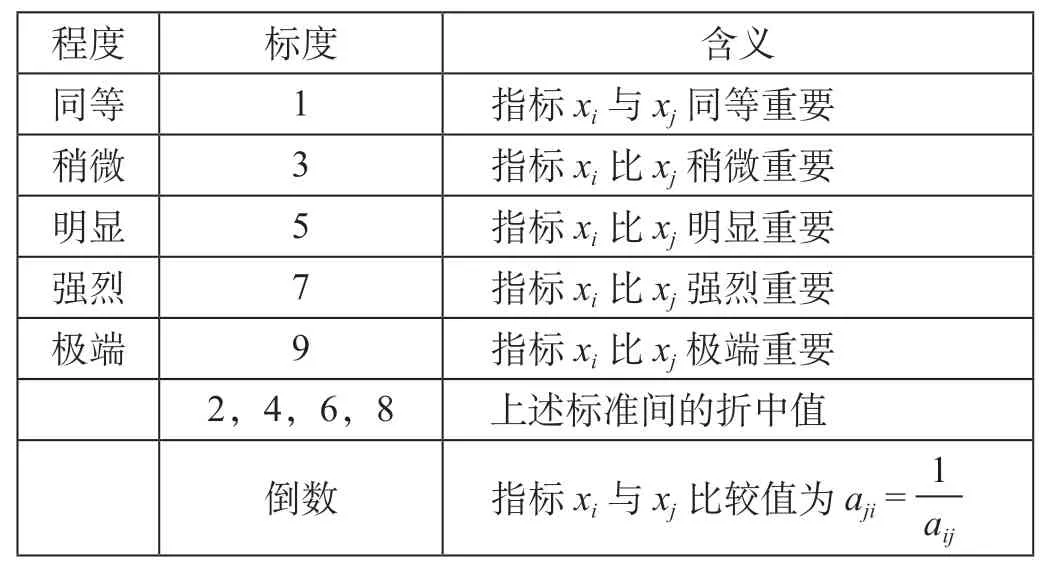
表2 AHP评价尺度表Tab.2 Evaluation scale of AHP

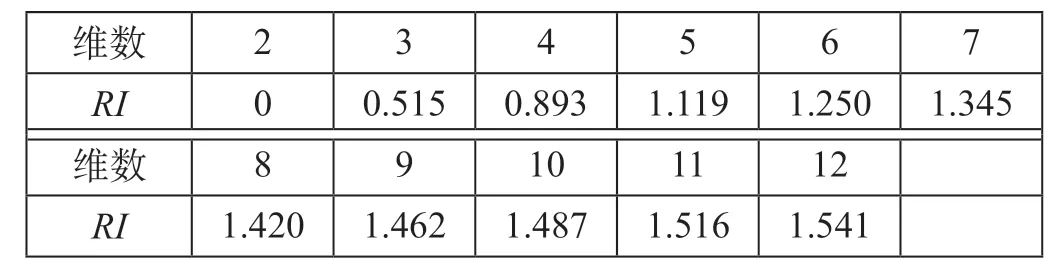
表3 随机一致性指标RI具体值Tab.3 Random consistency index

2.1.3 博弈论组合赋权法权重确定

为杜绝各种赋权方法得到的权重在一定显著水平下无显著性差异，在组合权重前，需要进行一致性检验。研究采用距离函数的方法来对2种方法得到的权重进行一致性检验。

设距离函数计算公式为

引入博弈论的思想，将2种赋权法的权重进行组合，使得两者组合后的权重更加均衡、合理[9]。组合赋权法的权重确定思路如下：设L种赋权法所得的指标权重构成的基本权重集为U= {u1，u2，…，uk)，k个向量的任意组合为优化权重系数αk，寻找最满意的权重向量u*，即其最优化一阶导数条件为计算组合系数集{α1，α2，…，αL}，并对其进行归一化处理得出基于博弈论思想的组合权重

2.2 城市轨道交通运营水平评价计算模型

构建城市轨道交通运营水平评价计算模型，使得计算出来的结果更能反映真实情况，计算方法如下。

式中：m为城市轨道交通运营水平评价值；Ii为第i个指标的无量纲值；wi为第i个指标对于总目标的权重，且u*= (w1，w2，…，wn)T。

将城市轨道交通运营水平评价值m计算结果分为“优”“良”“中”“差” “劣”5个等级，城市轨道交通运营水平评价等级如表4所示，根据计算结果参照评价标准来确定城市轨道交通运营状况。

表4 城市轨道交通运营水平评价等级Tab.4 Index grades of urban transit operation

3 实证分析

3.1 指标权重计算

根据建立的指标体系，选取2013—2017年上海、广州、南京、沈阳、成都、西安6个城市5年的数据做分析，得到各城市轨道交通的运营水平情况。所有数据均来源于MOPES中的实际数据，其中极少部分缺失数据由官方获取。

运用层次分析法，通过专家打分构造判断矩阵，将判断矩阵中的元素归一化后计算得到各要素的权重向量和最大特征根后，检验各层次判断矩阵的一致性，若满足一致性检验，则归一化后的特征向量即为各指标的权重。一级准则层的判断矩阵及权重值如表5所示，二级指标层客运服务系统的判断矩阵及权重值如表6所示，二级指标层基础运行系统的判断矩阵及权重值如表7所示，二级指标层能耗成本系统的判断矩阵及权重值如表8所示。

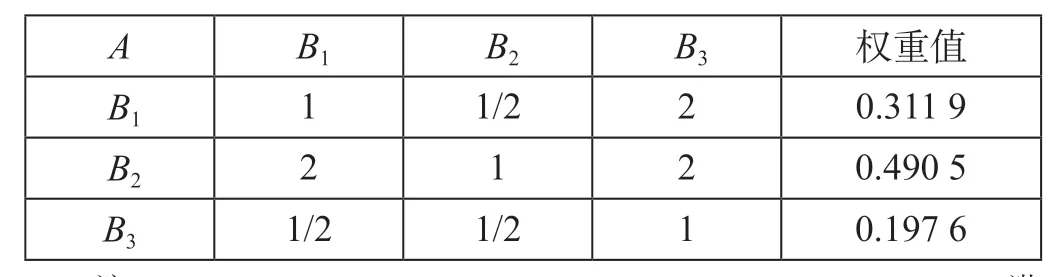
表5 一级准则层的判断矩阵及权重值Tab.5 Judgement matrix and weight values of the first-order criterion layer

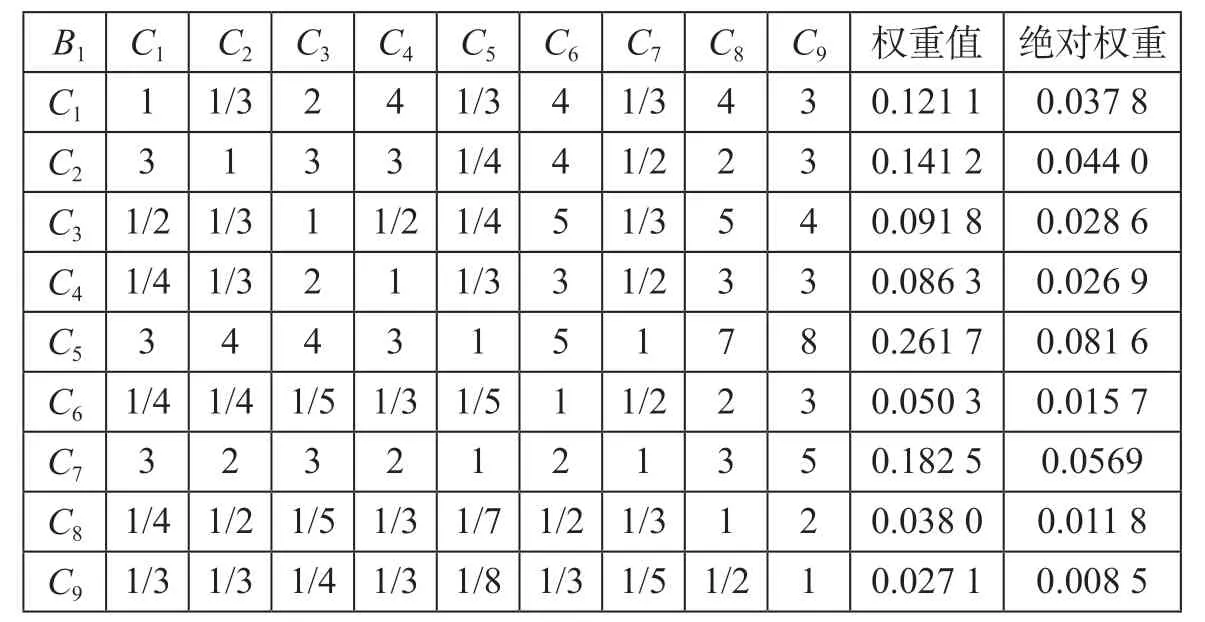
表6 二级指标层客运服务系统的判断矩阵及权重值Tab.6 Judgement matrix and weight values of the passenger service system in the second-order index layer

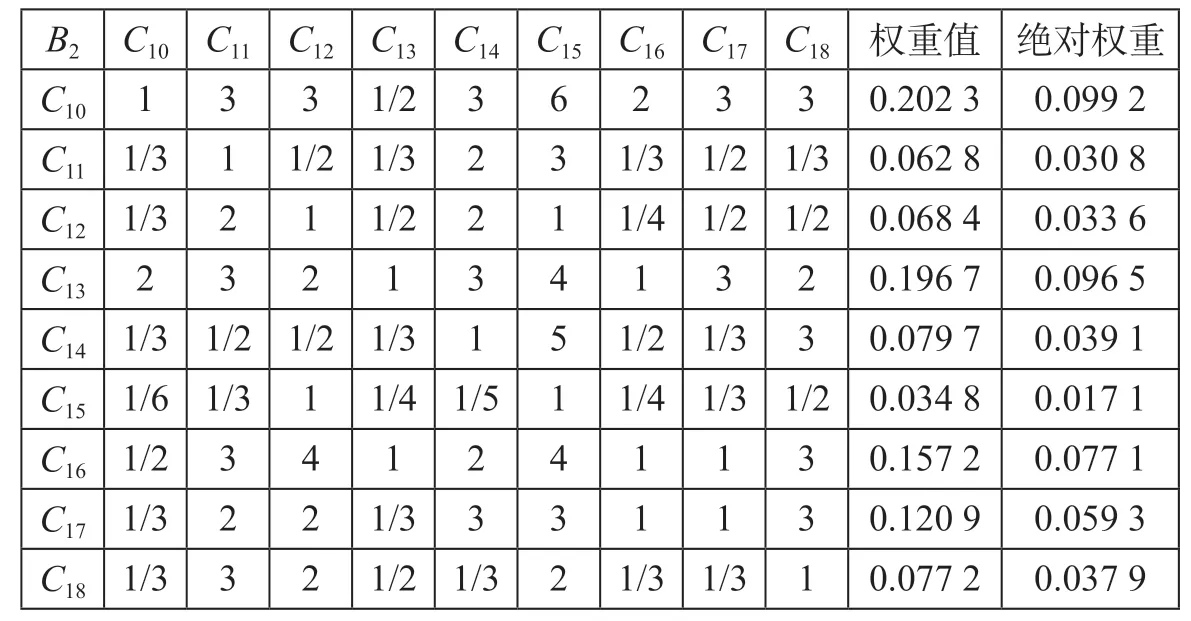
表7 二级指标层基础运行系统的判断矩阵及权重值Tab.7 Judgement matrix and weight values of the basic operation system in the second-order index layer

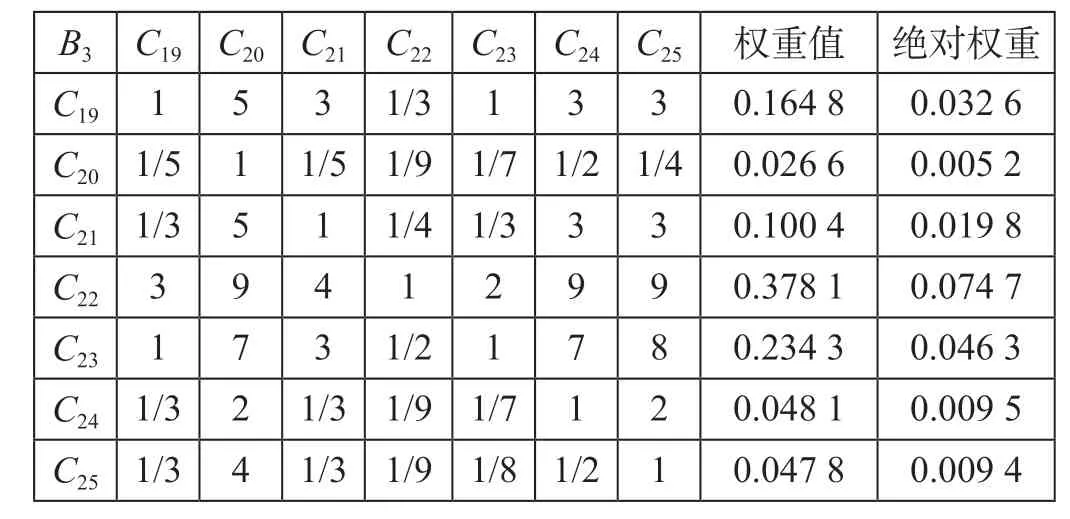
表8 二级指标层能耗成本系统的判断矩阵及权重值Tab.8 Judgement matrix and weight values of the energy cost system in the second-order index layer

经过计算，上述各层级的判断矩阵均满足一致性检验。另外，对层次总排序进行一致性检验，得CR= 0.084 9 ＜ 0.1，同样也满足一致性检验，说明各指标的权重值均有效。

利用熵值法计算各指标权重，各赋权方法计算的权重结果如表9所示。

在进行组合赋权融合前，需要将各种赋权法得到的权重进行一致性检验，若检验通过，则可以进行融合。利用公式⑴计算距离函数d(w(1)，w(2)) = 0.090 3 ∈ [0，1]，满足一致性检验。

由AHP和熵值法计算得到的各指标权重可以组成一个基本的权重向量集，利用公式 ⑵ 计算博弈论思想下的组合赋权权重，各赋权方法计算的权重结果见表9，城市轨道交通运营水平评价指标组合权重比例如图2所示。

从表9、图2分析可知，整个城市轨道交通运营系统中，客运服务系统各指标组合权重之和为0.308 0，基础运行系统各指标组合权重之和为0.501 4， 能耗成本系统各指标组合权重之和为0.190 6， 说明基础运行系统对运营系统的发展起到至关重要的作用。就单个指标而言，运营长度的组合权重值排名第一，为0.104 0，说明运营长度是整个运营系统发展的最重要指标；其次是日均运营里程为0.101 0、日均旅客周转量为0.084 8、日均开行列次为0.08及运营总成本为0.077 2，这5个指标的组合权重之和为0.447，接近整个系统权重的1/2，说明上述5个指标为影响整个运营系统的关键因素。

3.2 m值计算

根据表9的赋权结果和各指标无量纲值，运用公式⑶计算各城市不同年度在组合－博弈论思想下的m值。组合-博弈论思想下的城市轨道交通运营水平评价值分别如表10、图3所示。

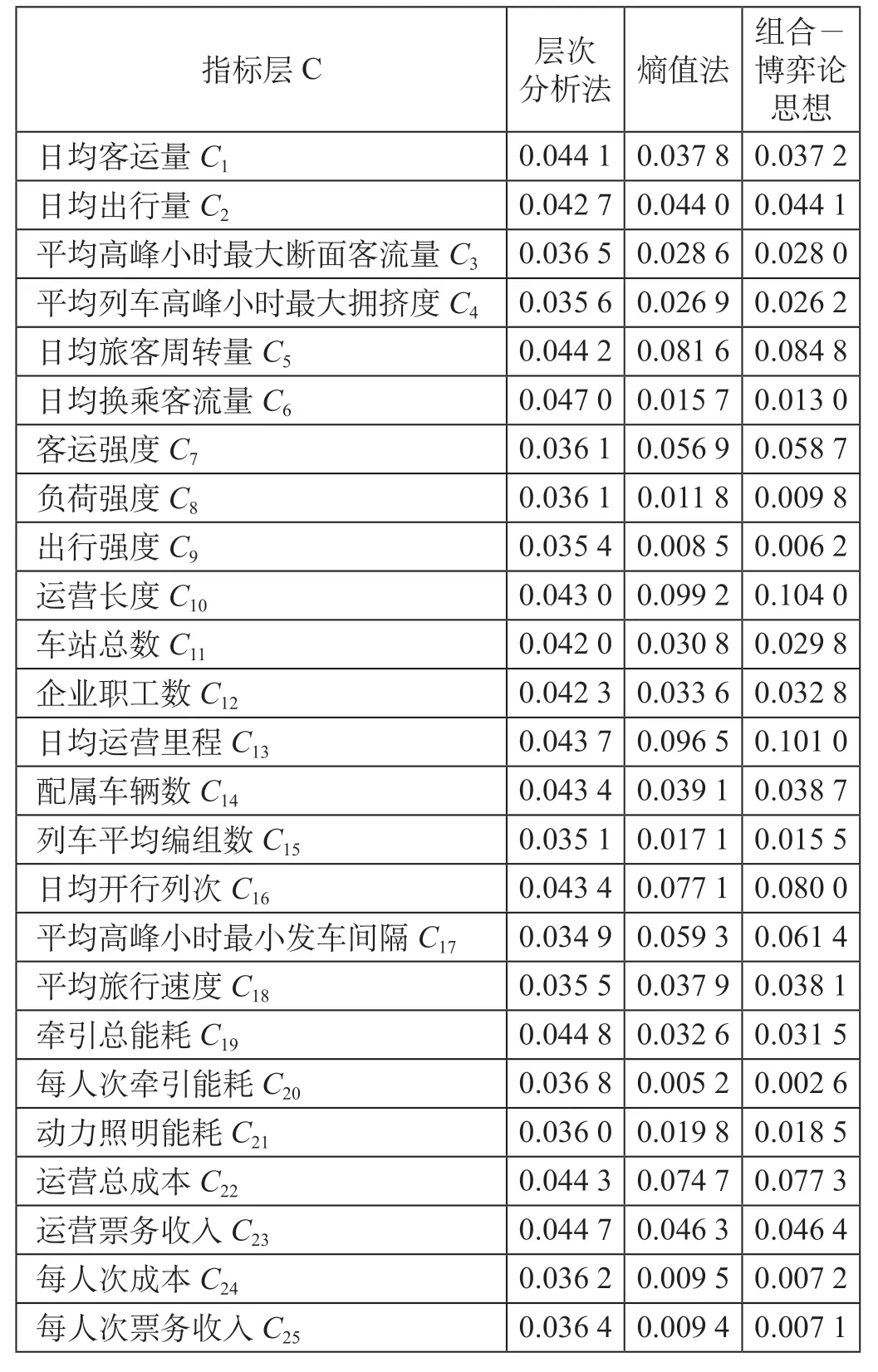
表9 各赋权方法计算的权重结果Tab.9 Weights calculated by each weighting method

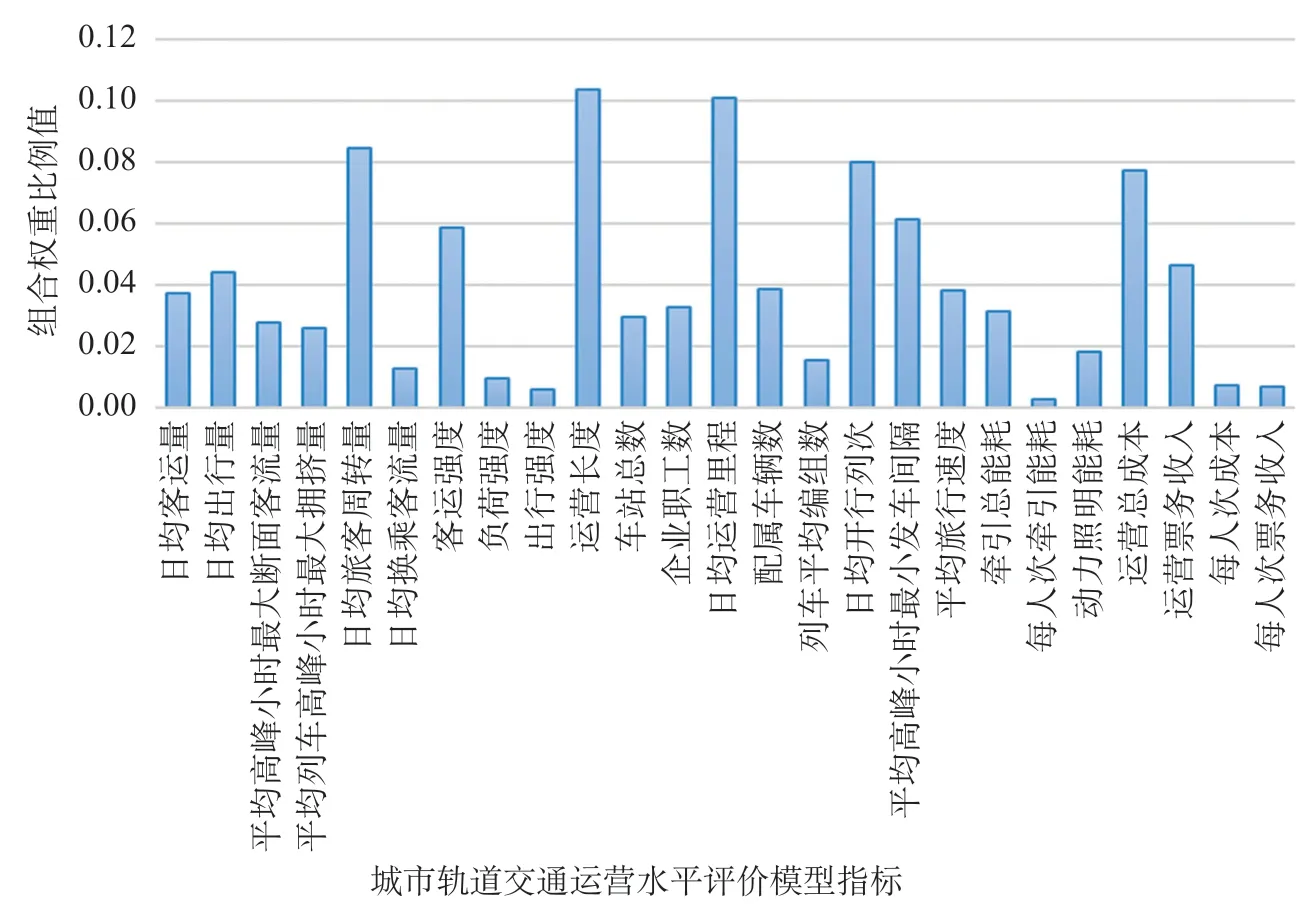
图2 城市轨道交通运营水平评价指标组合权重比例Fig.2 Combination weighting ratios of urban transit operation indexes

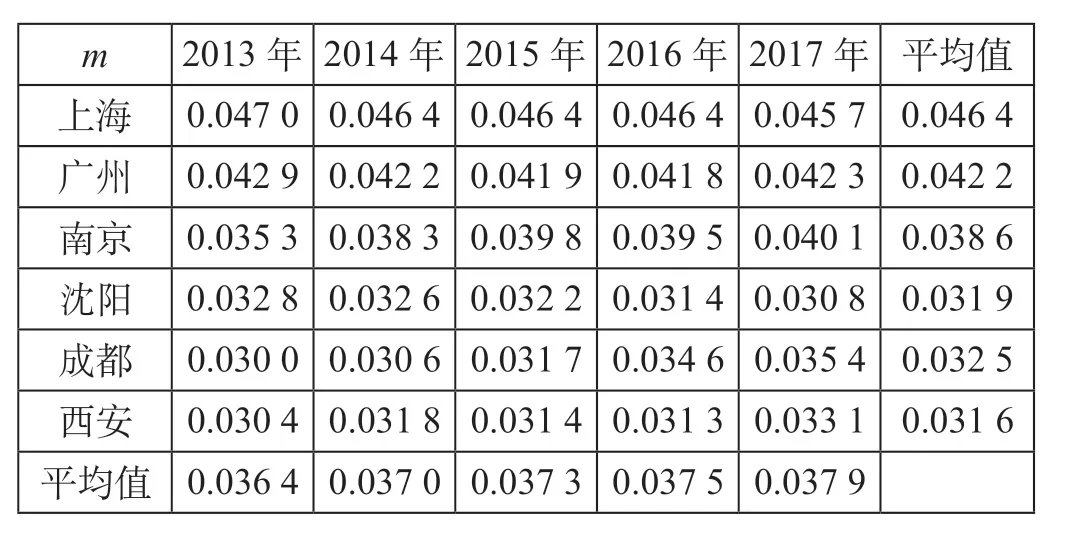
表10 组合-博弈论思想下的城市轨道交通运营水平评价值Tab.10 Urban transit operation indicators based on combination-game theory

从表10可以看出，2013—2017年间，m值均值呈上升趋势，其中，上海均值最高，为0.046 4， 西安均值最低，为0.031 6。整体来看，2013年上海的m值最高，为0.047 0，属于“良好”等级，2013年成都的m值最低，为0.030 0，属于“中等”等级。

3.3 结果分析

（1）从图3可以看出，以上海、广州为代表的网络化运营型城市轨道交通，其m值较其他类型的运营系统高，变化不显著，说明城市轨道交通发展到一定路网规模后，增加线路对其影响不大，其m值将趋于稳定。以南京、成都为代表的快速发展型城市轨道交通，其m值呈明显上升趋势，并且随着网络的形成，其m值已接近广州，说明在快速形成网络化过程中，m值也会随着线网的增加而迅速增大。以沈阳、西安为代表的非网络化运营型城市轨道交通，其m值相对较低，趋势变化也不大。

（2）在同一类型的城市轨道交通系统中，2013—2017年间，上海各年度的m值均高于广州，南京各年度的m值均高于成都，沈阳和西安呈上下波动趋势。说明在城市轨道交通路网快速扩张的过程中，城市轨道交通运营水平与城市轨道交通运营规模呈现正相关的关系，非网络化运营型城市轨道交通运营发展情况存在不稳定性，受地区经济、政策、环境等因素影响较大。

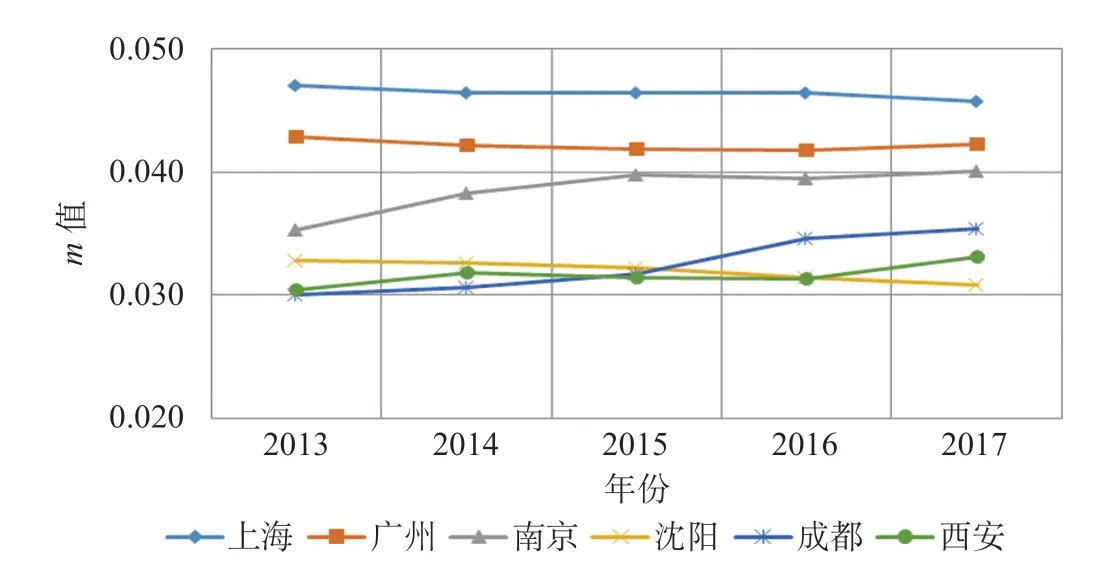
图3 组合-博弈论思想下的城市轨道交通运营水平评价值Fig.3 Urban transit operation indicators based on combination-game theory

（3）从图2可以看出，运营长度、日均运营里程、日均旅客周转量、日均开行列次及运营总成本等指标对城市轨道交通运营系统影响较大，可以通过关键指标的适量调节，来提高城市轨道交通运营水平。

（4）以上海、广州为代表的网络化运营型m值整体上明显高于快速发展型和非网络化运营型城市，因此，对于非网络化运营和快速发展的城市轨道交通运营企业而言，以网络化运营型城市为参照，将对提升运营水平有积极作用。

4 结束语

随着我国城市轨道交通建设不断加快，城市轨道交通运营发展不同形态体现出不同的水平差异。针对城市轨道交通运营发展量化评价，深度挖掘影响城市轨道交通运营发展的关键因素，提出应用组合赋权方法构建城市轨道交通运营水平评价模型，对城市轨道交通运营系统发展水平进行量化评价，直观体现出不同类型城市轨道交通运营系统的差异性，为城市轨道交通企业提升运营发展水平提供改善路径，为管理部门评价城市轨道交通运营发展水平提高参考依据。