考虑客流波动条件下高速铁路 票额分配鲁棒性模型研究
武晋飞,游雪松,薛 冰
(1.中国铁道科学研究院集团有限公司 电子计算技术研究所,北京 100081;2.中国国家铁路集团有限公司 客运部,北京 100844)
0 引言
符合高速铁路运行区段客流需求的客运供给数量直接受到票额预分方案的影响,票额分配方案的重要原则体现在合理利用列车坐席的条件下使其分配结果与客流需求相匹配,需要解决的核心问题是将有限的票额资源合理分配给各始发—终到站间(即OD)的客流。
根据票额分配策略的异同及分配阶段的划分方式等特点[1-2],学者们对铁路票额分配方案的优化方法进行了研究。张琦等[3]建立多列车限售策略和票额预分模型,实现多列车限售时段、限售区段和票额预分方案的联合优化设计。王洪业等[4]基于列车逐日分席别的客流预测方法,建立站间票额数量调配模型对票额进行分配。包云等[5]构建单列车客流预测的需求表达式,并将预测模型嵌入随机票额分配模型,通过求解客流量的期望值,将随机问题转化为确定性问题进行票额分配的计算求解。单杏花等[6]采用时间序列方法建立客流预测模型,基于先按数量预分再按比例预分原则,研究票额动态预分算法。You[7]假定每一支OD都可以分成全价区段和打折区段,旨在为所有票额类型都寻求一个预定限制,求解方法为启发式算法。
基于铁路客运服务的主要OD流量矩阵每天都会波动的实际情况,研究构建考虑客流波动条件下高速铁路票额分配鲁棒性模型,在充分满足基础客流分布的条件下研究票额预分,使得预分的票额与可能出现的波动客流总体匹配性较好,以抵消客流波动的影响,满足客流需求并保障铁路运输企业的经营效益。
1 考虑客流波动条件下高速铁路票额分配鲁棒性模型
1.1 票额分配
兼顾基础OD流量及波动OD流量条件进行票额合理分配问题与不考虑波动客流时直接进行票额分配问题,主要区别在于前者可能使票额分配结果与基础流量存在一定的偏差,从而使分配结果在充分满足基础流量的基础上为可能出现的客流波动做出预留,这部分票额偏差称为缓冲票额。
鲁棒性是指对于问题的一个解,在问题条件(参数)发生变化时该解依然具有较好的适用性。票额分配鲁棒性问题需要同时确定每个OD客流分到的基础票额数和缓冲票额数,缓冲票额数的意义为在基础票额数的基础上进行OD客流间更深层次的票额分配优化。考虑波动客流的票额分配如图1所示。如图1中的客流构成,由于波动场景中的AB客流与AC客流存在数量增加的可能性,AD客流存在数量减少的可能性,AD客流在逻辑关系上可以对AB客流、AC客流的票额进行补充。图1中给出2种可行的票额分配方案,基础票额数与缓冲票额数之和即总票额数,都是190张,但方案1考虑客流波动,方案2仅考虑基础客流。如果以票额与客流的差值的平方和来比较票额与客流的不匹配程度,虽然方案1基础票额与基础客流的不匹配程度(350)大于方案2基础票额与基础客流的不匹配程度(150),但考虑客流波动时,各OD客流的总票额与波动客流的总不匹配程度为方案 1 (240)小于方案2 (1 030)。因此,综合基础客流与波动客流的总不匹配程度,方案1 (590)小于方案 2 (1 180)。由此说明在基础票额构成的基础上,以其中部分票额作为缓冲票额在相关联的OD客流间进一步调整分配方案,可以使得在波动场景下实际客流量与基础票额分配结果间的偏差尽可能的小,即票额分配方案的鲁棒性尽可能地得到平衡[8]。

图1 考虑波动客流的票额分配Fig.1 Ticket allocation with fluctuating passenger flow
由以上分析可知,研究票额分配鲁棒性问题可以在票额预分时充分考虑客流波动因素的影响,使票额分配结果在充分匹配基础OD客流的同时,为可能出现的波动客流预留出应对空间。该方法对实际运营中铁路票额预分的指导意义在于,实现特定时间段内按预测特性出现的波动客流与票额分配方案的累积匹配度最高,即确保铁路运输企业面对每日复杂多变的客流时,在特定时间段内铁路票额供给与实际客流量的累积偏差最小。
1.2 模型构建
假设高速铁路列车运行区段中相邻车站间构成的列车运行区间集合为Q,用于确定该铁路区段列车开行方案的客流始发—终到站点对(即OD)集合为M。对于M集合中任意一个OD元素m∈M,其基础流量数值为αm。运行径路范围中包含区间集合Q中任意元素q(q∈Q)的OD所组成的集合为Pq,显然Pq为M的子集。令Nm为选定运行时间段内客流m(m∈M)可能出现的波动客流场景的集合,对于Nm中客流波动场景元素n∈Nm,令其波动流量数值为βn。βn可以通过相应的统计规律或短时预测数据进行样本点选取。列车的坐席数量为T。各OD流量对应分配的缓冲票额表示该OD及与其路径相关联OD间票额相互分拨时的可协调程度,允许的缓冲票额数量越大则最终的分配方案越有可能达到更加理想的效果,令M集合中任意一OD元素m(m∈M)分配到的基础票额数的上限比例为Rm,换言之,1 -Rm为OD元素m(m∈M)可以分配到的缓冲票额数的上限比例。另外,由于缓冲票额数可以为负数,因而令OD元素m(m∈M)的缓冲票额数可以选取的负数下限为Lm。令决策变量xm为OD元素m(m∈M)所分配的基础票额数,决策变量ym为OD元素m(m∈M)所分配的缓冲票额数。当铁路运输企业为客流分配的票额数与流量比较一致时,则旅客不仅可以最大程度地减少出行成本,而且铁路运输企业也可以最大程度地发挥高速铁路旅客运输的社会责任以及获得最大效益,由此建立客流波动条件下高速铁路票额分配的鲁棒性优化模型为

Z为目标函数值,目标函数(1)由2部分构成:第1部分为模型所分配的基础票额数与基础客流量的不匹配程度最小,即票额分配结果尽可能地符合基础客流需求,此部分目标称为基础目标值,μ1为基础目标值的权重参数;第2部分为在考虑客流波动的场景下,票额分配的结果与各波动场景下的客流需求的总不匹配程度最小,此部分目标表示票额分配方案在客流波动时的鲁棒性,称为鲁棒性目标值,μ2为鲁棒性目标值的权重参数,票额分配结果需要根据目标权重的参数取值将这2部分目标综合协调。约束条件(2)、约束条件(3)分别表示在列车运行各区间内,各OD的基础票额数取值需要满足与其他具有相同运行区间OD的基础票额总数不超过列车坐席定额数,以及基础票额与缓冲票额的代数和需要满足与其他具有相同运行区间OD的基础票额与缓冲票额代数和不超过列车坐席定额数。缓冲票额数的适当增加可以提高票额分配结果的鲁棒性,但过大的缓冲票额取值会对基础目标值产生较大影响;反之,基础票额数取值范围较大可以生成基础目标值更好的票额分配方案,然而,可选的缓冲票额数较小会对鲁棒性目标值产生不利影响。因此,约束条件(4)限定每个OD的基础票额的取值上限,约束条件(5)限定每个OD的缓冲票额的取值上限,由于缓冲票额数可以为负,因此约束条件(6)对缓冲票额的取值下限进行限定。缓冲票额取值为负的含义是从基础票额数中扣除一部分分配给某OD对应可供给集合中的各OD,因而扣除部分不可以超过基础票额数,因此约束条件(7)限定当缓冲票额为负数时,基础票额与缓冲票额的代数和不小于0。约束条件(8)是基础票额取值的非负约束。
1.3 模型求解
根据模型非线性的特点,设计模拟退火算法对模型进行求解,该算法的核心环节是邻域的构建,模型邻域系虽然可以在整个可行票额组合区域内进行设计,但这样会导致搜索范围较大,且解的质量不能得到保证,因而对邻域系进行预设。具体步骤如下。
步骤1:初始化。设置初始温度B>0,以及内层最大迭代次数。
步骤2:邻域构建。对于列车运行途中的每一个区间q(q∈Q),由于受OD基础票额上限取值约束以及区间q所有OD基础票额之和的取值约束,因而令区间q的当前分配票额Tq为
总的来说,在当前煤机维修企业发展中,人力资源的开发管理是非常关键的。我们应该从科学的角度入手,做好对煤机维修企业人力资源管理工作的优化,为企业自身经济效益的发展提供良好的基础保障。

式中:R为该区间的所有OD票额取值限制参数Rp(p表示区间q对应OD集合Pq中的元素)中的最小值。
经过区间q的所有OD基础票额取值为Tq的一个随机全划分,Tq的一个随机全划分为
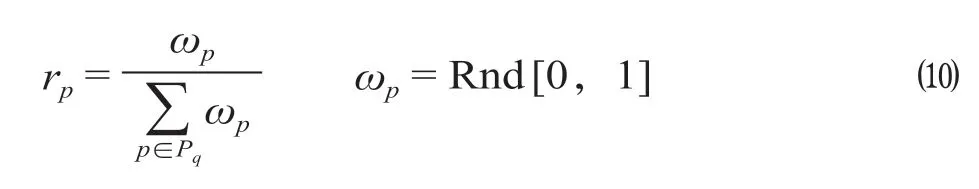
式中:rp为随机票额取值比例;ωp为0 ~ 1之间的随机数。
令区间q对应OD集合Pq中的元素p的基础票额数的临时取值为xp,q,xp,q计算公式为

各OD的基础票额的最终取值xm为

更新区间q当前可分配票额Tq为

由于各OD实际分配到的基础票额数之和可能小于基础票额的上限数,因而可以充分利用基础票额分配后的剩余部分,即进一步更新Tq。
对于区间q对应OD集合Pq中的元素p,如果以一定的概率取值为负数,则该OD的缓冲票额yp取值计算公式为

否则,统计当前缓冲票额取值为负数的个数,并记为ly,按照公式(10)生成随机全划分{r1,r2,…,r|Pq|-ly},令此区间缓冲票额值不为负数的OD元素p缓冲票额数的临时取值yp,q计算公式为

式中:rp为随机全划分向量{r1,r2,…,r|Pq|-ly}中的元素。
各OD的缓冲票额的最终取值ym为

步骤3:判断当前解是否满足符合概率计算式的接受条件。
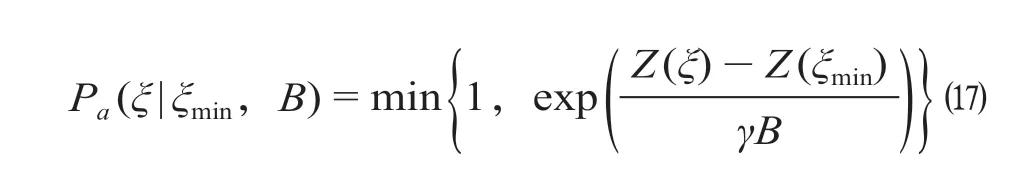
式中:Pa(ξ|ξmin,B)为当前温度B下接受新可行解的概率;ξ为当前生成的票额分配方案;ξmin为当前最优票额分配方案;Z(ξ)为当前生成的票额分配方案的目标函数值;Z(ξmin)为当前最优票额分配方案的目标函数值;γ为温度系数,取值根据目标函数的数量级及所要求的算法运行时效进行确定。
步骤4:更新内层循环。如果迭代终止条件满足(可以用退火温度来控制),计算结束,否则更新温度B=φB,降温系数φ∈ (0,1),转步骤2。
2 案例分析
2.1 基础OD流量与波动OD流量数据
假设某高速铁路列车上行途中共经停4个车站,列车运行方向上共有6个OD客流,列车运行方向基础OD流量与波动OD流量矩阵如表1所示。各OD的基础客流量如表1括号外数据所示,如果假设基础OD流量所生成的波动OD场景为10个,各OD在不同波动场景下波动客流量如表1括号内数据所示,令这些波动客流的集合为波动客流组1,以下首先基于该组波动客流进行高速铁路票额分配鲁棒性模型的票额计算。
2.2 考虑客流波动条件下票额分配鲁棒性求解
首先令基础目标值权重μ1改变时对模型求解得到算法收敛曲线,算法收敛曲线如图2所示。令考虑客流波动条件下票额分配鲁棒性模型的求解记为MT,当不考虑缓冲票额时模型退化为仅仅对基础票额数对应的基础目标值进行评估,记为MB,基础目标权重改变下不同求解模型的结果比较如表2所示。由图2可得,当基础目标值的权重μ1增加时,模型的总目标值增加,但如表2所示,随着基础目标值权重的增加,基础目标值在被选择时的灵敏度增加,模型求解结果对应的基础目标值也随之呈下降趋势,最后趋于平缓,说明模型求解出具有较好基础目标值的票额分配方案的可能性增加。从表2中还可以看出,模型所得解中鲁棒性票额为负数的现象较为常见,说明相比于基础目标而言,鲁棒性目标需要通过缓冲票额将基础票额数减少一部分。另外,模型MT的结果与MB的结果进行比较可得,MT分配方案的鲁棒性目标明显优于MB分配方案的鲁棒性目标,说明在模型中加入缓冲票额的决策可以使得模型的求解结果在出现客流波动条件下具有较好的鲁棒性。

表1 列车运行方向基础OD流量与波动OD流量矩阵 人次Tab.1 Basic OD matrix and fluctuating OD matrix in train running direction

图2 算法收敛曲线Fig.2 Convergence curve of the algorithm

表2 基础目标权重改变下不同求解模型的结果比较Tab.2 Comparison among the results of different solution models with varying basic objective weights
(1)波动客流组1基础目标值比较。改变模型中基础票额最大比例参数Rm对模型进行求解,波动客流组1基础目标值比较如图3所示。从图3中可以看出随着基础票额最大比例参数的增加,模型求解结果中基础目标值的质量呈下降趋势,这是由于基础票额最大比例参数增加时用于分配给基础票额部分的坐席增加。另外,随着该参数的增加,模型倾向于用所有的坐席进行基础票额的分配,因此MT分配方案与MB分配方案的求解方案变得相似,基础票额数以及基础目标值趋近于一致。
(2)波动客流组1鲁棒性目标值比较。改变模型中基础票额最大比例参数Rm对模型进行求解,波动客流组1鲁棒性目标值比较如图4所示。从图4可以看出,随着基础票额最大比例参数的增加,缓冲票额可以占用的票额比例减少,因此所求得的票额分配方案的鲁棒性目标值也在相应地变差,且缓冲票额比例越小,模型MT的分配方案与MB的分配方案的鲁棒性目标值越接近,说明缓冲票额比例的设定对票额分配结果的鲁棒性目标值具有非常重要的作用。此外,在相同的参数设置条件下,模型MT的票额分配方案的鲁棒性呈现出明显优于MB方案的鲁棒性的特性,且缓冲票额的可用比例较大。因此,模型MT的票额分配方案具有较好的鲁棒性优势。
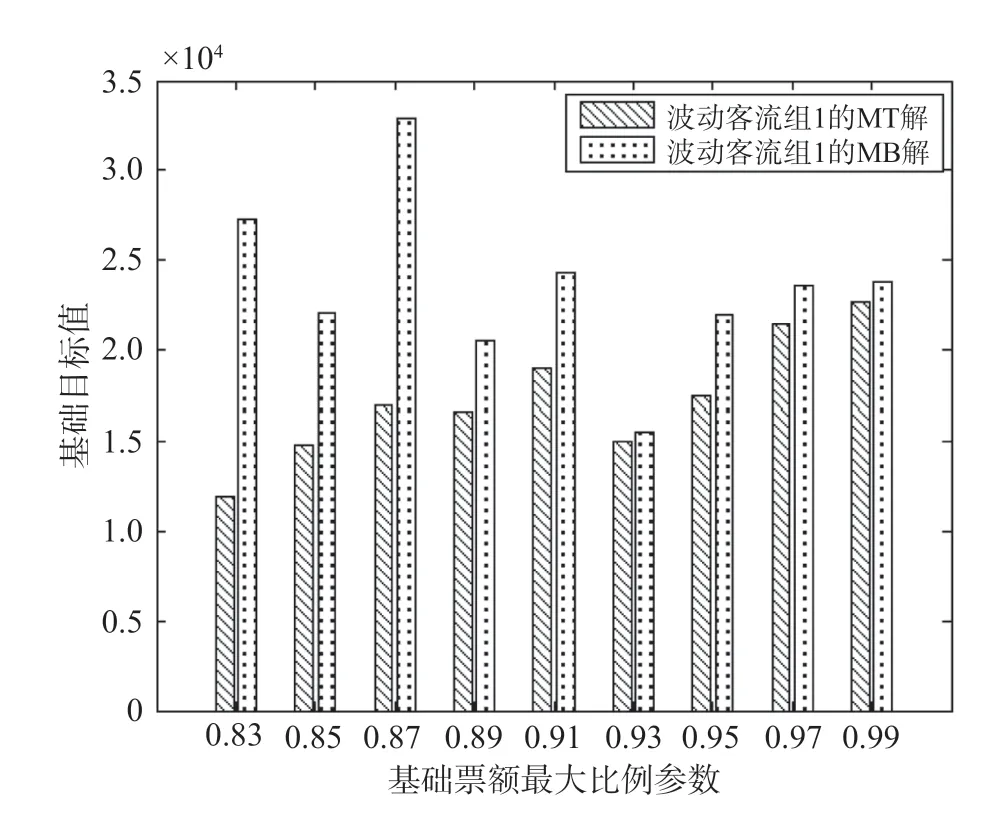
图3 波动客流组1基础目标值比较Fig.3 Comparison among basic objective values in Group 1 of fluctuating passenger flow

图4 波动客流组1鲁棒性目标值比较Fig.4 Comparison among robustness objective values in Group 1 of fluctuating passenger flow
2.3 有效性验证
为了进一步验证考虑客流波动条件下高速铁路票额分配鲁棒性模型方法的有效性,在波动客流组1的基础上更换新的客流波动数据Nm构建波动客流组2进行模型求解。当改变缓冲票额的取值范围参数时,波动客流组2基础目标值与鲁棒性目标值比较如图5所示。为了使模型求解结果的特点更加明显,求解时将鲁棒性目标值的权重μ2设置为较大参数。从图5b中依然可以看出随着缓冲票额取值范围参数的增加,模型MT票额分配策略的鲁棒性目标呈现出降低趋势,且由于目标函数中鲁棒性目标权重较大,因而MT票额分配策略的鲁棒性目标值明显优于MB策略的鲁棒性目标值。此外,由于模型的鲁棒性目标权重及缓冲票额可用比例参数较大,从图5显示的结果可以看出,建立的MT模型求解策略可以求解出综合协调基础目标值以及鲁棒目标值的最优解,从而验证方法的有效性。

图5 波动客流组2基础目标值与鲁棒性目标值比较Fig.5 Comparison between basic objective values and robustness objective values in Group 2 of fluctuating passenger flow
由2组算例可知,模型以波动客流组Nm为输入参数,表示在日常运营中实际发生符合相似规律的客流变化时与不考虑客流波动的模型求解策略相比,考虑客流波动条件下的票额分配鲁棒性模型制定出的票额预分方案一方面可以使客流发生波动时预分票额与波动客流的总偏差量(鲁棒性)较优,同时该方案又符合该时期主要客流的分布特点,即票额预分方案的基础目标值同时得到兼顾,这使得票额预分方案可以在较长时期内具有较高普适性。从模型的求解过程也可以看出:缓冲票额的可取值范围参数越大,所得分配方案的鲁棒性越好;模型目标函数中鲁棒性部分的权重越大,所得分配方案的鲁棒性目标所占主导位置更明显,即鲁棒性越好。
3 研究结论
(1)铁路票额分配问题是一个较为复杂的组合优化问题,票额分配结果不仅需要最大限度地满足基础客流的出行需求,还需对于可能出现的波动客流量尽可能地保持受到的影响最小,即需要确保票额分配方案的鲁棒性尽可能的大。在实际运营中,票额鲁棒分配方案可以在一段时期内具有与实际客流的总匹配性较好的效果。
(2)确保票额分配方案具有较好鲁棒性的关键是在票额分配结果中合理优化缓冲票额的分配。缓冲票额体现了所得分配方案对基础客流以及各种波动客流的综合考虑。缓冲票额所占总票额的最大比例会影响票额分配方案鲁棒性的优劣,与不设置缓冲票额的分配策略相比较,研究设计的鲁棒性票额分配模型可以求解出兼顾基础目标质量以及鲁棒性目标质量的票额分配方案。
(3)票额分配鲁棒性模型中不同权重、参数等取值会对模型求解结果产生明显影响。在实际应用中可以针对所研究铁路线路(区段)的客流量、OD个数、客流波动规律等实际情况,综合确定模型中所采用的具体参数取值,从而求解出满足实际运营需求并与整体客流规律相匹配的票额分配方案。

