有界线性算子及其函数的a-Browder定理

王 宁，曹小红

(陕西师范大学 数学与统计学院，陕西 西安710119)

算子理论是泛函分析的重要组成部分，而算子谱理论又是算子理论的重要组成部分.1909年，Weyl在研究Hilbert空间上自伴算子的谱时，给出了Weyl定理[1].在接下来的研究中，学者们一方面研究一些特殊算子的Weyl定理[2-8]，一方面对Weyl定理进行变形.目前为止，Weyl定理的变形包括Browder定理、a-Weyl定理以及a-Browder定理，Weyl定理及其变形称为Weyl型定理，对Weyl型定理及其相关性质的研究一直是算子谱理论的研究热点[9-16].本文将着手于a-Browder定理的相关问题，探究有界线性算子及其函数满足a-Browder定理的等价条件.

1 预备知识

谱σ (T)={λ∈C:T-λI不是可逆算子}；

上半Fredholm谱σSF+(T)={λ∈C:T-λI不是上半Fredholm算子}；

逼近点谱σa(T)={λ∈C:T-λI不是下有界算子}；

Fredholm谱σe(T)={λ∈C:T-λI不是Fredholm算子}；

Weyl谱σw(T)={λ∈C:T-λI不是Weyl算子}；

Browder谱σb(T)={λ∈C:T-λI不是Browder算子}；

本质逼近点谱σea(T)={λ∈C:T-λI不是上半且i nd(T-λI)≤0的算子}；

Browder逼近点谱σab(T)={λ∈C:T-λI不是上半且升标有限的算子}；

Saphar谱σS(T)={λ∈C:T-λI不是Saphar算子}.

特别地，Goldberg定义了谱集

σG(T)={λ∈C:T-λI值域不闭}[14]；

算子T的Kato谱可以表示为

σK(T)=σS(T)∪σG(T);

不可逆的Browder算子组成的集合记作 σ0(T)=σ(T)σb(T).

预解集为

ρ(T)=Cσ(T);

类似地，其它谱对应的预解集定义为该谱集在复数域中的补集，分别记作

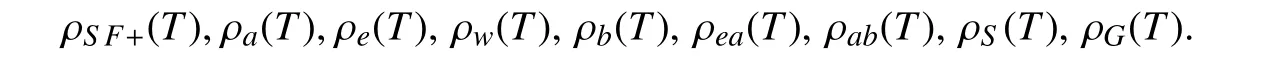
对复平面中的任意集合E，用 isoE表示E中孤立点的全体，intE表示E中内点的全体，accE表示E中聚点的全体， ∂E表示E中边界点的全体.在本文中，D 表示单位闭圆盘，Γ表示单位圆周.

2 有界线性算子的a-Browder定理

下面，我们将借助σ5(T) 来研究算子及其函数的a-Browder定理.

定理1设T∈B(H)，则下列叙述等价：

(1)T满足a-Browder定理；

(2)σ (T)=σ5(T)∪{λ∈isoσa(T):n(T-λI)≤d(T-λI)}∪[ρa(T)∩σ(T)]；

(3)σ(T)=σ5(T)∪isoσa(T)∪[ρa(T)∩σ(T)].

证明(1)⇒(2)任取

于是 μ∈ρa(T)，λ0∈ρa(T)∪isoσa(T).若 λ0∈isoσa(T)， 则n(T-λ0I)＞d(T-λ0I)， 因此T-λ0I为Fredholm算子.由Fredholm算子摄动定理可知， ind(T-λ0I)=ind(T-μI)＞0，这与 ind(T-μI)≤0矛盾.因此 λ0∈ρa(T)，由于 λ0∉[ρa(T)∩σ(T)]， 所以 λ0∉σ(T)， 因此 σ (T)⊆σ5(T)∪{λ∈isoσa(T):n(T-λI)≤d(T-λI)}∪[ρa(T)∩σ(T)].反包含显然.

(2)⇒(3) 显然.

(3)⇒(1) 要证T满足a-Browder定理，只需证ρea(T)⊆ρab(T).任取λ0∈ρea(T)， 则λ0∈ρ5(T)，断言λ0∈ρa(T)∪isoσa(T).事实上，若λ0∉ρa(T)∪isoσa(T)，λ0∉σ(T)，λ0∈ρ(T)⊆ρa(T)， 这与λ0∉ρa(T)矛盾.当λ0∈ρa(T)∪isoσa(T)时，T在λ0处有单值延拓性质，于是 a sc(T-λ0I)＜∞， 因此λ0∈ρab(T).证毕.

注1(1)由定理1可知，当T满足a-Browder定理时，

其中σ (T)分解的3部分缺一不可.

例1令T∈B(ℓ2)定义为：T(x1,x2,x3,···)=(x2,x3,x4,···)，则

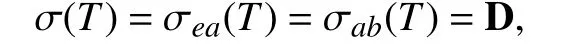
即T满足a-Browder定理.但由于

即T满足a-Browder定理.但由于σ5(T)=ρa(T)∩σ(T)=Ø，故

例3令T∈B(ℓ2)定义为：T(x1,x2,x3,···)=(0,x1,x2,x3,···)，则

即T满足a-Browder定理.但由于

σ(T)=D,{λ∈isoσa(T):n(T-λI)≤d(T-λI)}=Ø,

故σ(T)≠σ5(T)∪{λ∈isoσa(T):n(T-λI)≤d(T-λI)}.

(2) 设T∈B(H)， 由定理1知，当σ (T)=σ5(T)时，T满足a-Browder定理.反之不成立，如例3.

(3)设T∈B(H)， 则σ(T)=σ5(T)当且仅当T满足a-Browder定理，σ(T)=σa(T)且{λ∈isoσ(T):

n(T-λI)＜∞}=Ø.

事实上，若σ (T)=σ5(T)， 根据定理1，T满足a-Browder定理；由 ρa(T)⊆ρ5(T)=ρ(T)以及{λ∈isoσ(T):n(T-λI)＜∞}⊆ρ5(T)=ρ(T)可知σ (T)=σa(T)且 {λ∈isoσ(T):n(T-λI)＜∞}=Ø.

反之，若T满足a-Browder定理且σ(T)=σa(T)， 则ρ5(T)⊆ρ(T)∪isoσ(T)，由于{λ∈isoσ(T):n(TλI)＜∞}=Ø，故 ρ5(T)⊆ρ(T)，因此σ (T)=σ5(T).证毕.

(4) 设T∈B(H)， 则σ (T)=σ5(T)∪σG(T)∪σ0(T)当且仅当T满足a-Browder定理且σ (T)=σa(T).

事实上，若 σ(T)=σ5(T)∪σG(T)∪σ0(T)，由于 ρea(T)∩[σ5(T)∪σG(T)]=Ø， 则 ρea(T)⊆σ0(T)∪ρ(T)，ρea(T)⊆ρab(T)，于是σea(T)=σab(T)， 故T满足a-Browder定理.由ρa(T)∩[σ5(T)∪σG(T)∪σ0(T)]=Ø=ρa(T)∩σ(T)知， ρa(T)⊆ρ(T)，于是σ (T)=σa(T).

反之，任取λ0∉σ5(T)∪σG(T)∪σ0(T)， 则T-λ0I上半Fredholm算子且λ0∈ρ5(T)，由于T满足a-Browder定理且σ(T)=σa(T)， 则λ0∈ρ(T)∪isoσ(T)，故λ0∈ρb(T)，又由于λ0∉σ0(T)，则λ0∉σ(T)，因此σ(T)⊆σ5(T)∪σG(T)∪σ0(T).反包含显然.证毕.

(5) 设T∈B(H)， 则σ (T)=σ5(T)∪isoσ(T)当且仅当T满足a-Browder定理且σ (T)=σa(T).

接下来，我们对定理1中T满足a-Browder定理的等价条件继续进行整理.

推论1设T∈B(H)，则下列叙述等价：

证明(1)⇒(2) 由定理1知，σ(T)=σ5(T)∪isoσa(T)∪[ρa(T)∩σ(T)]. 因为 σ5(T)=accσ5(T)∪isoσ5(T)，T满足a-Browder定理，则ρ5(T)⊆ρa(T)∪isoσa(T)，于是

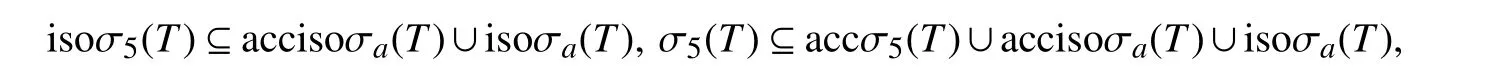
从而σ (T)⊆accσ5(T)∪accisoσa(T)∪isoσa(T)∪[ρa(T)∩σ(T)].反包含显然.

(2)⇒(3)由于

同时

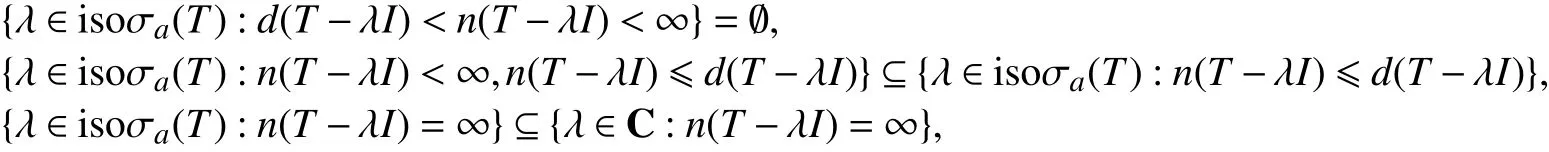
因此

反包含显然.

断言此时， λ0∈ρa(T)∪isoσa(T).

事实上，若λ0∉ρa(T)∪isoσa(T)， 则λ0∉σ(T)，λ0∈ρ(T)⊆ρa(T)，这与λ0∉ρa(T)矛盾.当λ0∈ρa(T)∪isoσa(T)时，T在λ0处有单值延拓性质，于是 a sc(T-λ0I)＜∞，因此λ0∈ρab(T).证毕.

在注1的(4)中，我们将σG(T)也用于算子的a-Browder定理的判定中，下面继续这方面的工作.

推论2设T∈B(H)，则下列叙述等价：

(1)T满足a-Browder定理；

(2)σ (T)=σ5(T)∪σG(T)∪σ0(T)∪{λ∈ρab(T):n(T-λI)＜d(T-λI)}；

(3)σ(T)=σ5(T)∪σK(T)∪[ρa(T)∩σ(T)].

证明(1)⇒(2)任取

则易知λ0∈ρ5(T)∩ρG(T)， 于是T-λ0I是上半Fredholm算子且i nd(T-λ0I)≤0，因为T满足a-Browder定理，所以λ0∈ρab(T). 由于 λ0∉{λ∈ρab(T):n(T-λI)＜d(T-λI)}， 故 in d(T-λ0I)=0，因此 λ0∈ρw(T). 由于T满足a-Browder定理，则T-λ0I升标有限， λ0∈ρb(T).但λ0∉σ0(T)，因此λ0∉σ(T).反包含显然.

(2)⇒(3) 由于{ λ∈ρab(T):0＜n(T-λI)＜d(T-λI)}∩ρK(T)=Ø，故

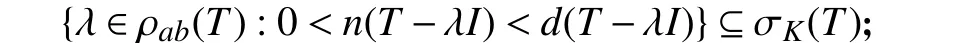
同时

因此σ (T)⊆σ5(T)∪σK(T)∪[ρa(T)∩σ(T)].反包含显然.

(3)⇒(1) 只需证 ρea(T)⊆ρab(T).任取 λ0∈ρea(T)， 由半Fredholm算子摄动定理可知，存在ε＞0，当 0＜|μ-λ0|＜ε时， μ∉σ5(T)∪σK(T)，于是 μ∈ρa(T)∩σ(T)或 μ∈ρ(T)，总之 μ∈ρa(T)，则 λ0∈ρa(T)∪isoσa(T)，T在λ0处有单值延拓性质，于是 a sc(T-λ0I)＜∞，因此λ0∈ρab(T).证毕.

注2在推论2中，当T满足a-Browder定理时，

其中σ (T)分解的4部分缺一不可.

在例1中， σ(T)=σea(T)=σab(T)=D， 即T满足a-Browder定理.但由于

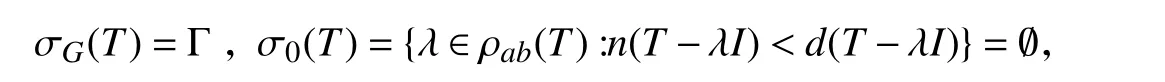
故σ(T)≠σG(T)∪σ0(T)∪{λ∈ρab(T):n(T-λI)＜d(T-λI)}.

在例2中， σ(T)=σea(T)=σab(T)={0}， 即T满足a-Browder定理.但由于

故σ(T)≠σ5(T)∪σ0(T)∪{λ∈ρab(T):n(T-λI)＜d(T-λI)}.

在例3中，σ5(T)=σG(T)=σea(T)=σab(T)=Γ，即T满足a-Browder定理.但由于σ(T)=D，σ0(T)=Ø，故σ (T)≠σ5(T)∪σG(T)∪σ0(T).

例4设A,B∈B(ℓ2) 的定义为：

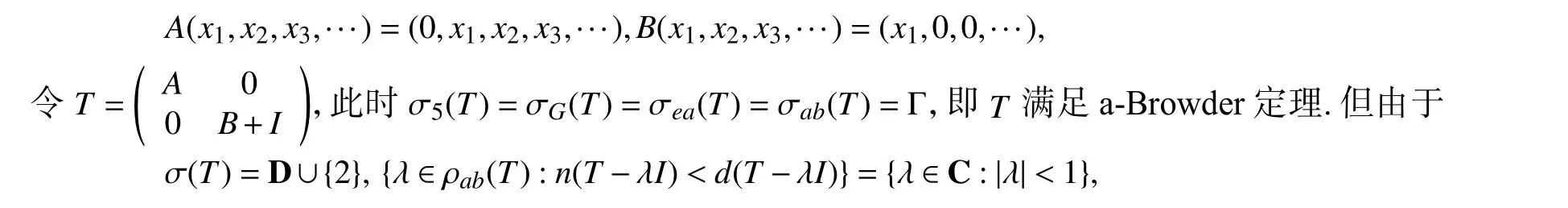
故σ(T)≠σ5(T)∪σG(T)∪{λ∈ρab(T):n(T-λI)＜d(T-λI)}.

3 算子函数的a-Browder定理

我们知道，当算子满足a-Browder定理时，并不能推出算子函数满足a-Browder定理.下面，我们就利用σ (T)和σ5(T) 之间的关系研究算子函数的a-Browder定理.

定理2设T∈B(H)， 则任给多项式p，p(T)满足a-Browder定理当且仅当T满足a-Browder定理且下列之一成立：

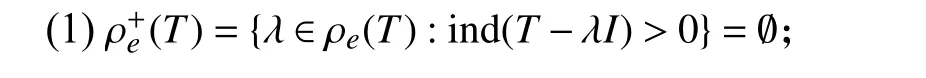
(2)accσ(T)⊆σ5(T).

证明 必要性.若任给多项式p，p(T)满足a-Browder定理，则T满足a-Browder定理，若此时(1)、(2)均不成立，则存在λ1∈ρe(T)， 使得i nd(T-λ1I)=n＞0(n为正整数)，同时存在λ2∈accσ(T)∩ρ5(T)；因为T满足a-Browder定理，则存在ε＞0及λ3∈C满足 0＜|λ3-λ2|＜ε，使得λ3∈ρa(T)∩σ(T)， 则ind(T-λ3I)=-m＜0(m为正整数或者m=+∞) . 令p(T)=(T-λ1I)m(T-λ3I)n(m为正整数)或p(T)=(T-λ1I)(T-λ3I)(m=+∞)，于是p(T)为上半Fredholm算子且 ind(p(T))≤0. 由于p(T)满足a-Browder定理，则p(T)升标有限，于是T-λ1I升标有限， ind(T-λ1I)≤0，这与 i nd(T-λ1I)＞0矛盾.因此，(1)和(2)至少有一个成立.

于是{ λ∈ρSF+(T):ind(T-λI)＜0}=Ø，故任给λ ∈ρSF+(T)，有i nd(T-λI)≥0.

综上，任给λ ∈ρSF+(T),μ∈ρSF+(T)，有i nd(T-λI)·ind(T-μI)≥0.

下证任给多项式p,p(T)满足a-Browder定理.设μ ∈ρea(p(T))，令

其中λi≠λj(i≠j)，1 ≤i,j≤k.于是T-λiI(1≤i≤k) 是上半Fredholm算子，由

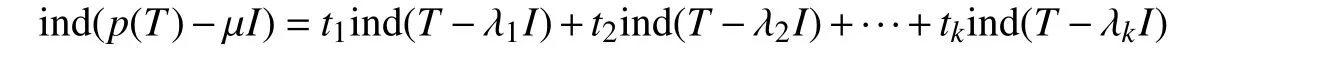
知，ind(T-λiI)≤0，于是λi∈ρea(T)，由于T满足a-Browder定理，则T-λiI升标有限，故asc(p(T)-μI)＜∞， 于是ρea(p(T))⊆ρab(p(T))，故σea(p(T))=σab(p(T))， 即任给多项式p，p(T)满足a-Browder定理.证毕.

推论3设T∈B(H)， 则任给多项式p，p(T)满足a-Browder定理当且仅当T满足a-Browder定理且下列之一成立：

(1)σ5(T)⊆σe(T)；

(2)accσ(T)⊆σ5(T).

注3(1)设T∈B(H)， 当σ(T)=σ5(T)， 由定理1知，T满足a-Browder定理，又由于此时accσ(T)⊆σ5(T)， 由定理2知，任给多项式p，p(T) 满足a-Browder定理.但任给多项式p，p(T) 满足a-Browder定理，并不能推出σ (T)=σ5(T)，如例3.

由注1中的(3)及推论3知：

(2)设T∈B(H)， 则σ(T)=σ5(T) 当且仅当任给多项式p，p(T)满足a-Browder定理，σ(T)=σa(T)且{λ∈isoσ(T):n(T-λI)＜∞}=Ø.

(3)设T∈B(H)， 则任给多项式p，p(T)满足a-Browder定理并且 σ(T)=σa(T)当且仅当σ(T)=σ5(T)∪isoσ(T).(4)设T∈B(H)， 若T满足a-Browder定理且σ (T)=σa(T)， 则任给多项式p，p(T)满足a-Browder定理.在定理2和推论3中，我们借助σ5(T) 来刻画算子函数的a-Browder定理，下面我们考虑能否借助intσ5(T)来刻画算子函数的a-Browder定理呢?

定理3设T∈B(H)， 则任给多项式p，p(T)满足a-Browder定理当且仅当T满足a-Browder定理且下列之一成立：

(1)i ntσ5(T)⊆σe(T)；

(2)intσ(T)=intσ5(T).

证明 必要性显然.

注4(1)设T∈B(H)， 若 intσ(T)=intσ5(T)， 由于 ρea(T)∩intσ5(T)=Ø=ρea(T)∩intσ(T)，于是ρea(T)⊆ρ(T)∪∂σ(T)，由半Fredholm算子摄动定理知，ρea(T)⊆ρb(T)⊆ρab(T)， 因此σea(T)=σab(T),T满足a-Browder定理，由定理3知，任给多项式p，p(T)满足a-Browder定理.但任给多项式p，p(T)满足a-Browder定理，并不能推出i ntσ(T)=intσ5(T)，如例3.

(2) 设T∈B(H)， 则 i ntσ(T)=intσ5(T)当且仅当任给多项式p，p(T)满足a-Browder定理且 σ (T)=σa(T).

(3)设T∈B(H)， 存在 λ0∈ρSF+(T)，使得 int(T-λ0I)＞0，则任给多项式p，p(T)满足a-Browder定理当且仅当i ntσ(T)=intσ5(T).

事实上，若任给项式p，p(T)满足a-Browder定理，存在λ0∈ρSF+(T)，使得 ind(T-λ0I)=n＞0(n为正整数),断言σ (T)=σa(T).

若不然，则存在 μ0∈σ(T)σa(T)， 于是 μ0∈ρa(T)且 ind(T-μ0I)=-m＜0(m为正整数或者m=+∞).

令p(T)=(T-λ0I)m(T-μ0I)n(m为 正整数)或p(T)=(T-λ0I)(T-μ0I)(m=+∞) ,于是p(T)为上 半Fredholm算子且 ind (p(T))≤0.由于p(T) 满足a-Browder定理，则p(T) 升标有限，于是T-λ0I升标有限，ind(T-λ0I)≤0，这与 i nd(T-λ0I)＞0矛盾.因此， σ(T)=σa(T)， 由注4的(2)可知 intσ(T)=intσ5(T).

反之，若i ntσ(T)=intσ5(T)，由注4的(1)可知，任给多项式p，p(T)满足a-Browder定理.证毕.

下面，我们尝试借助a ccσ5(T) 来刻画算子函数的a-Browder定理，可得如下结论：

定理4设T∈B(H)， 则任给多项式p，p(T)满足a-Browder定理当且仅当T满足a-Browder定理且下列之一成立：

(1)a ccσ5(T)⊆σe(T)；

(2)accσ(T)=accσ5(T)∪accisoσa(T).

证明 类似于定理2证明过程证明.证毕.

注5 (1)设T∈B(H)， 若a ccσ(T)=accσ5(T)，由于 ρea(T)∩accσ5(T)=Ø=ρea(T)∩accσ(T)，于是ρea(T)⊆ρ(T)∪isoσ(T)， 由半Fredholm算子摄动定理知，ρea(T)⊆ρb(T)⊆ρab(T)， 因此σea(T)=σab(T)，T满足a-Browder定理，由定理4知，任给多项式p，p(T)满足a-Browder定理.但任给多项式p，p(T)满足a-Browder定理，不能推出a ccσ(T)=accσ5(T)，如例3.

定义集合

（2）设T∈B(H)， 则 accσ(T)=accσ5(T)当且仅当任给多项式p，p(T)满足a-Browder定理，σ(T)=σa(T)并且E=Ø.

事实上，若 accσ(T)=accσ5(T)，易证任给多项式p，p(T)满足a-Browder定理， σ(T)=σa(T).下面说明E=Ø，若E≠Ø，设λ0∈E， 则存在ε ＞0，当 0 ＜|μ-λ0|＜ε时， μ∈ρ5(T)，于是λ0∉accσ5(T)=accσ(T)， 故λ0∉accisoσ(T)， 这与λ0∈E矛盾.因此E=Ø.

反之，若任给多项式p，p(T)满足a-Browder定理，要证a ccσ(T)=accσ5(T)，只需证a ccσ(T)⊆accσ5(T).任取 λ0∉accσ5(T)，由于T满足a-Browder定理且σ(T)=σa(T)， 则λ0∈{λ∈C:存在ε＞0当 0＜|μ-λ|＜ε时， μ∈ρ(T)∪isoσ(T)且n(T-μI)＜∞}， 由于E=Ø，故λ0∉accisoσ(T)， 于是存在ε＞0，当 0＜|μ-λ0|＜ε时，μ∈ρ(T)，因此λ0∉accσ(T).

(3)设T∈B(H)， 则accσ(T)=accσ5(T)∪accisoσ(T)当且仅当任给多项式p，p(T)满足a-Browder定理且σ (T)=σa(T).

接下来，我们借助∂ σ5(T) 继续来讨论算子函数的a-Browder定理.

定理5设T∈B(H)， 则任给多项式p，p(T)满足a-Browder定理当且仅当T满足a-Browder定理且下列之一成立：

(1)a ccσ5(T)⊆σe(T)；

(2)accσ(T)⊆∂σ5(T)∪accσea(T).

证明 必要性.根据a ccσ(T)=accσ5(T)∪accisoσa(T)⊆σ5(T)， 易证accσ(T)⊆∂σ5(T)∪accσea(T).根据定理4，必要性得证.

充分性.若T满足a-Browder定理且 ac cσ5(T)⊆σe(T)， 易证任给多项式p，p(T)满足a-Browder定理，并且 σ (T)=σa(T). 若 a ccσ(T)⊆∂σ5(T)∪accσea(T)，由于 ρa(T)∩[∂σ5(T)∪accσea(T)]=Ø， 则 ρa(T)∩accσ(T)=Ø，故 ρa(T)⊆ρ(T)∪isoσ(T).由半Fredholm算子摄动定理知， ρa(T)⊆ρ(T)，因此 σ(T)=σa(T).由注3的(4)可知，任给多项式p，p(T)满足a-Browder定理.证毕.

推论4设T∈B(H)， 则任给多项式p，p(T)满足a-Browder定理当且仅当T满足a-Browder定理且下列之一成立：

(1)i ntσ5(T)⊆σe(T)；

(2)intσ(T)⊆∂σ5(T)∪accσea(T).