数控机床单轴受力对反向间隙影响的研究

苏妙静，侯家林，刘 璨，刘焕牢

（机械与动力工程学院 广东海洋大学，湛江 524088）

0 引言

提高工件的加工精度是制造业不懈的追求，而高精度的数控机床是实现该目标的必经途径。通过对数控机床的误差测量，认识机床误差的特性，了解机床误差源，不仅能为机床重要零件的高精度制造提供依据，还能为机床的软件误差补偿提供基础参数。数控机床精度要求的不断提高，要求我们要对机床进行定期的误差补偿，以保证机床的整体加工精度[1]。

影响机床加工精度的误差，按照误差源可划分为：力变形误差、温度误差、几何误差、动态误差等[2～4]。而对于半闭环控制的数控机床，反向间隙是影响数控机床定位精度和重复定位精度的一个重要因素[5,6]，进而影响机床的加工精度和产品的加工质量，因此对数控机床反向间隙影响因素的研究显得尤为重要。反向间隙是几何误差中的重要组成部分，目前对其认识仍停留在静态阶段[7]。螺距误差和反向间隙可以通过软件补偿进一步提高数控机床的精度[8]。杜柳青等[9]利用圆形运动误差轨迹获取了反向间隙和周期误差等的特征矩阵；TsraelU.Ponce等[10]做了反向间隙在负载作用下引起的延迟、震动、冲击的研究；刘强等[11]针对一种五轴数控机床旋转轴的几何精度和反向间隙进行了测量。但是对于数控机床受力情况下反向间隙的研究相对较少。

基于以上分析，本文以数控机床Y轴为例，提出了一种数控机床单轴受力加载方案，采用激光干涉仪测量数控机床的定位误差，并通过计算得出相应加载条件下的反向间隙，分析在不同加载条件下反向间隙的变化情况，以及通过螺距误差、反向间隙补偿后不同加载条件下反向间隙的变化规律，同时观察定位精度和重复定位精度的变化趋势。

1 运用激光干涉仪的误差检测

1.1 误差测量方法的选择

本文使用了本研究团队[12]研究的一种新的9线线性误差测量方法（如图1所示）进行误差测量，该测量方法每次只能测量一种几何误差值，能够直接测量单个平动轴的六项几何误差值。相比较其他方法而言，该方法对光调节环节比较简单，且能直接测量获得各种误差数值，能够有效地避免了联动调节和误差模型等带来的偏差，使测量结果更加可靠和精确。

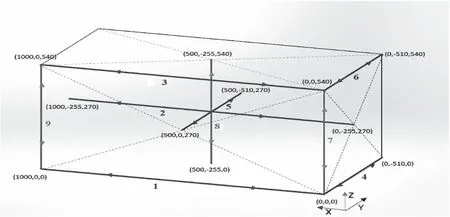
图1 新的9线直接测量方法

1.2 误差检测

激光干涉仪是目前数控机床误差测量精度最高的仪器，其不仅可以提供简单的直接测量方法，而且可以直接测量各项误差量，还可以验证其他测量方法的可靠性，而且对众多的误差模型的校核也是重要的途径。

本次实验采用Renishaw公司XL-80型激光干涉仪，并结合上述新的9线直接测量方法中的线段4来测量数控机床Y轴定位误差（如图2所示）。通过获得数据分析结果，并对FANUC系统的三轴立式数控加工中心进行螺距误差补偿、反向间隙补偿，再次测量补偿后的定位误差。由于后面加载装置的需要，本次实验Y轴的有效测量行程为300mm，按照国际标准ISO 230-1的要求，对不超过500mm的轴的测量间隙不大于20mm，对比较长的轴，建议测量间隙不超过轴长的1/10，以增加测量的点数，获取更多的样本。据此，本次定位误差测量往返5次，两个测量点的测量间隔为20mm。

图2 Y轴定位误差测量

2 数控机床单轴受力装置的设计

一般来讲，采用激光干涉仪直接测量单项误差的测量方法更准确，其原理更简单。但是在测量过程中对测量环境的要求比较严格，要求机床要处于“静态”状态，因此为了模拟数控机床实际切削过程中所受的切削力的加工过程，设计了恒定载荷的加载装置。通过恒定载荷装置给数控机床施加恒定力。

2.1 实验设备

以数控车间1台型号为VMC1000P的三轴立式数控加工中心为研究对象，该数控机床X轴的有效行程为1000mm，Y轴有效行程为510mm，Z轴有效行程为540mm。图3为实验所用数控机床，本次实验以Y轴为例进行。

图3 VMC100P三轴立式数控加工中心

2.2 加载装置的设计

为了加载实验过程的方便操作，加载装置分别由三角支架、定滑轮、钢丝绳、螺母、螺柱以及套筒等组成。使用螺栓将定滑轮固定于螺柱的顶端，定滑轮可绕其中心轴转动，螺柱通过上下两个螺母，将其固定于套筒中，完成上下移动的锁紧，并且可以通过调节两个螺母来调节加载装置的高度（保证钢丝绳和机床工作台处于平行状态），使用螺钉与螺柱上的键槽配合，完成螺柱转动方向的锁紧。为了加强加载装置强度，在三角支架之间焊接铁条，加载装置整体实物图如图4所示。

图4 恒定载荷加载实验图

2.3 恒定载荷的实际加载

采用标准砝码为本次实验加载对象，通过分析分别选用标准砝码组中的5kg、10kg、20kg、25kg的砝码进行实验（如图5所示）。钢丝绳的一段固定于机床工作台，另一端通过定滑轮连接砝码组，调节加载装置的位置，使施力方向与机床坐标轴Y轴共面；调节螺母和锁紧螺钉来调整加载装置的高度，使钢丝绳、定滑轮与机床工作台位于同一水平线上。通过运行CNC代码程序，使机床工作台带动钢丝绳在定滑轮的作用下使加载砝码做上下运动，通过砝码的重量模拟数控机床实际切削过程中所受的切削力。更换不同的砝码组，完成0kg、5kg、10kg、20kg、25kg加载条件下的定位误差的测量。其恒定载荷的实际加载实验图如图4所示。

图5 恒定载荷加载砝码

3 数控机床螺距误差和反向间隙补偿

3.1 反向间隙的计算

使用激光干涉仪测量并获得未补偿前数控机床Y轴的定位误差值，计算得出Y轴的单项平均位置偏差：

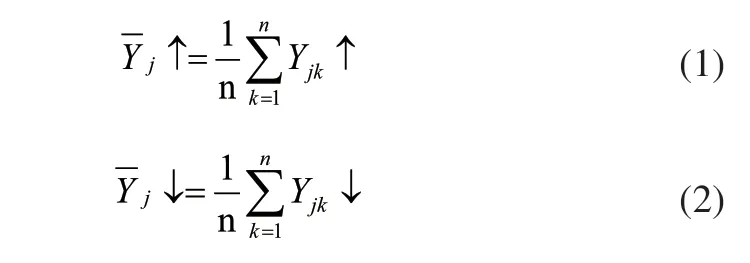
再计算得出数控机床Y轴双向平均位置偏差：

由此计算得出Y轴的反向偏差：

从而计算得出Y 轴线双向反向间隙：

3.2 螺距误差和反向间隙补偿

通过以上计算得出的反向间隙并进行补偿，同时通过激光干涉仪测量软件分析得出对应的螺距误差补偿图表，并按照要求将反向间隙补偿值和螺距误差补偿图表写入数控机床对应补偿位置。机床断电重新启动，螺距误差与反向间隙补偿生效，完成补偿。并再次使用激光干涉仪测量补偿后0kg、5kg、10kg、20kg、25kg加载条件下的定位误差。

4 实验结果分析

4.1 反向间隙结果分析

按照上述的测量操作，测量获得Y轴在0kg、5kg、10kg、20kg、25kg加载条件下的定位误差，以及经过螺距误差和反向间隙补偿的定位误差，通过计算得出相应的反向间隙如图6、图7所示。图中显示，Y轴反向间隙的变化范围为-11μm～4μm，经过螺距误差和反向间隙补偿后反向间隙的变化范围为-2μm～3μm，通过对比可以看出，补偿后的反向间隙明显提高。在加载条件下的具体变化如表1所示，可以得出，数控机床的反向间隙随着切削力的增大而减小，但通过螺距误差、反向间隙补偿后的反向间隙却随着切削力的增大而增大。

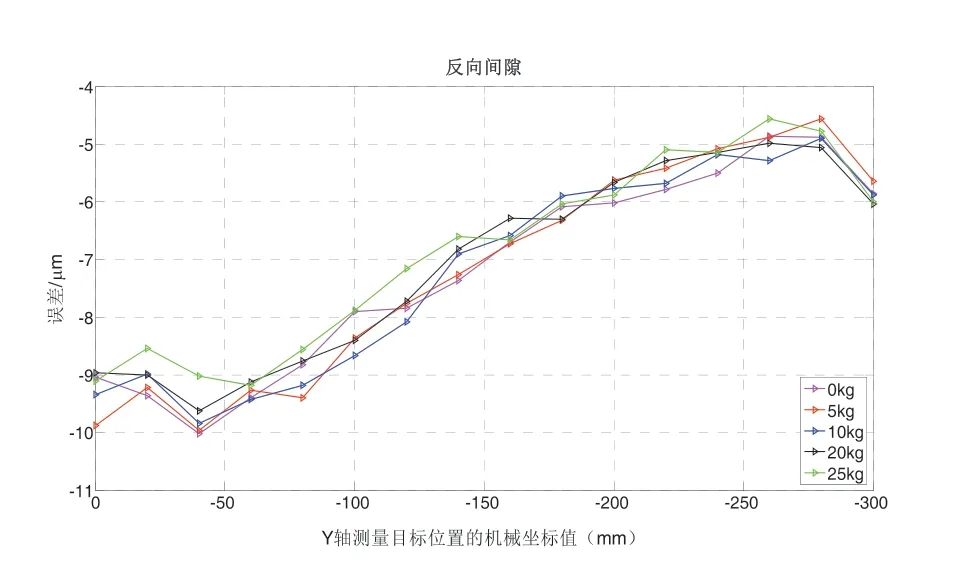
图6 Y轴反向间隙

图7 Y轴补偿后反向间隙

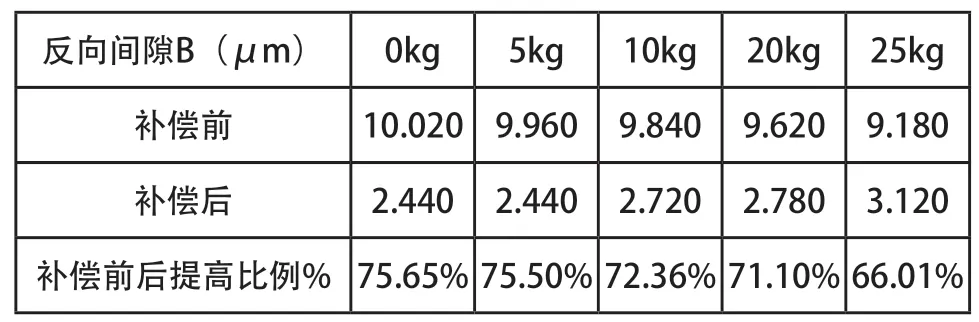
表1 反向间隙B补偿前后对比图表

由于数控机床的丝杠和丝母之间一定存在一定的间隙，所以在机床运动中，在正转后变换成反转的时候，在一定的角度内，尽管丝杠转动，但是丝母还要等间隙消除（受力一侧）以后才能带动工作台运动。因此在数控机床Y轴受到加载力的时，随着加载重量的不断增大，反向间隙不断增大，这是因为一开始反向间隙的产生在另一侧，经过反方向的受力，随着加载重量的不断增加，反向间隙反而减少。经过在0kg时螺距误差和反向间隙补偿后的反向间隙随着加载重量的不断增加，反向间隙也随之增大，因为此时反向间隙的产生与加载力的方向一致。

4.2 定位误差结果分析

按照上述的测量操作，测量得出Y轴0kg、5kg、10kg、20kg、25kg加载条件下的定位精度和重复定位精度，以及经过螺距误差和反向间隙补偿的定位精度和重复定位精度如图8～图17所示。

图8 0kg时Y轴定位误差

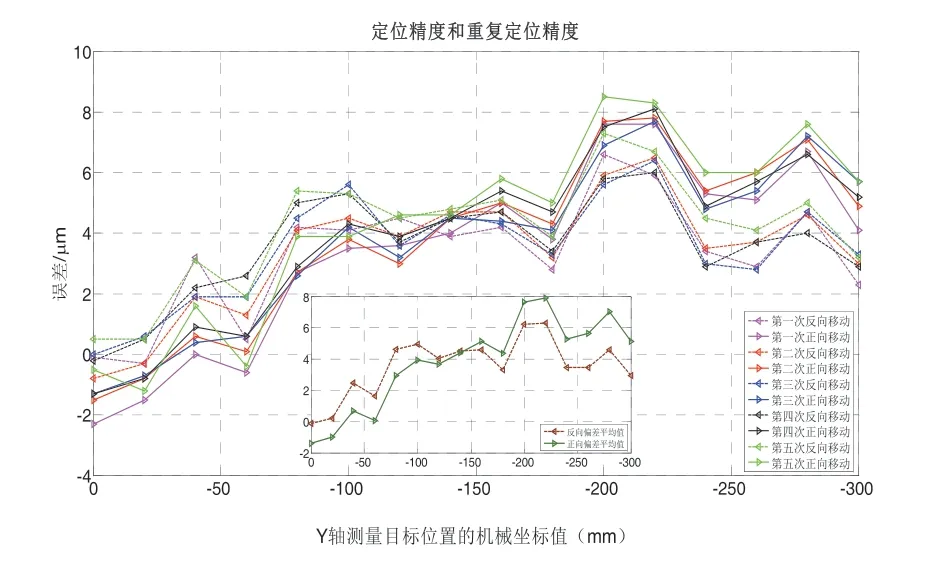
图9 0kg时Y轴补偿后定位误差

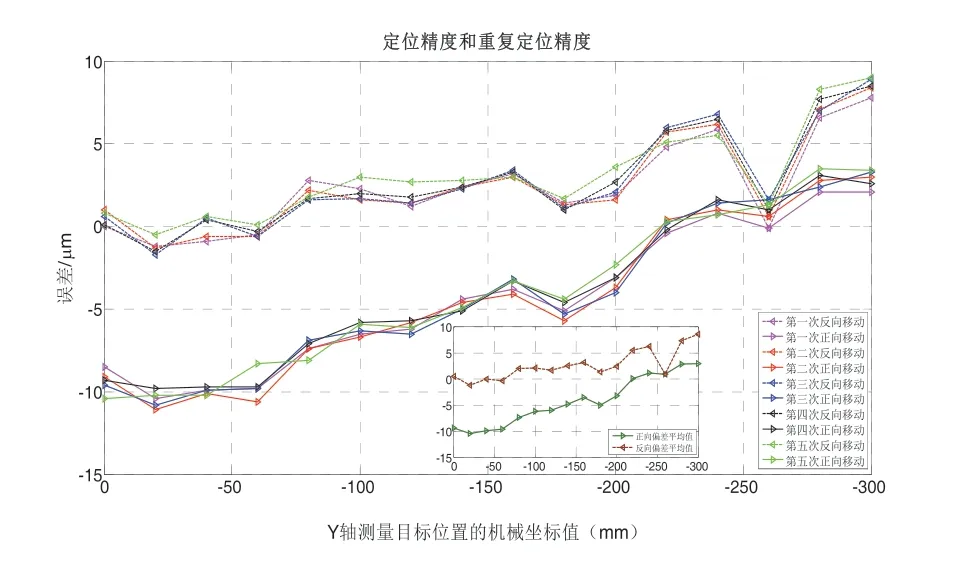
图10 5kg时Y轴定位误差

图11 5kg时Y轴补偿后定位误差

图12 10kg时Y轴定位误差

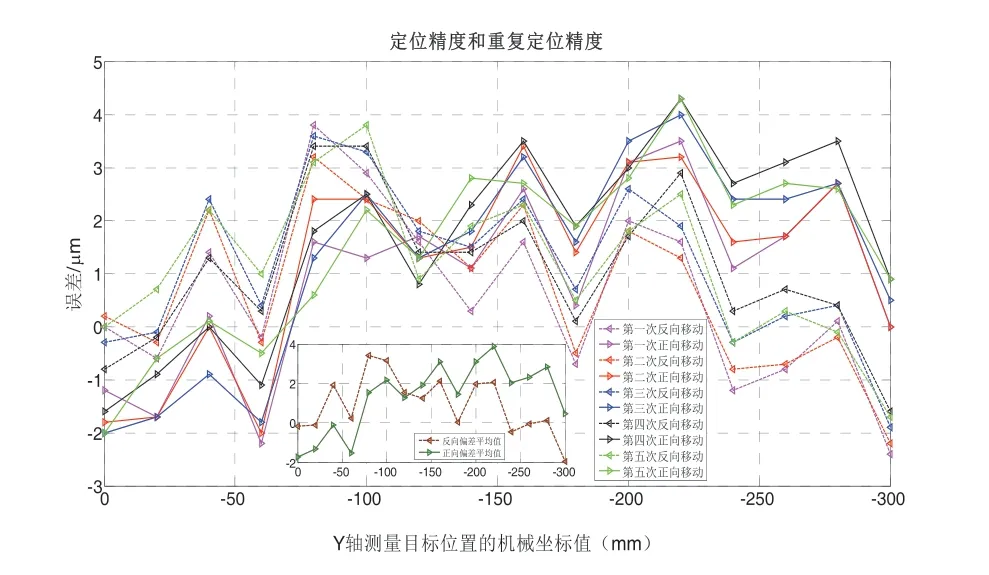
图13 10kg时Y轴补偿后定位误差

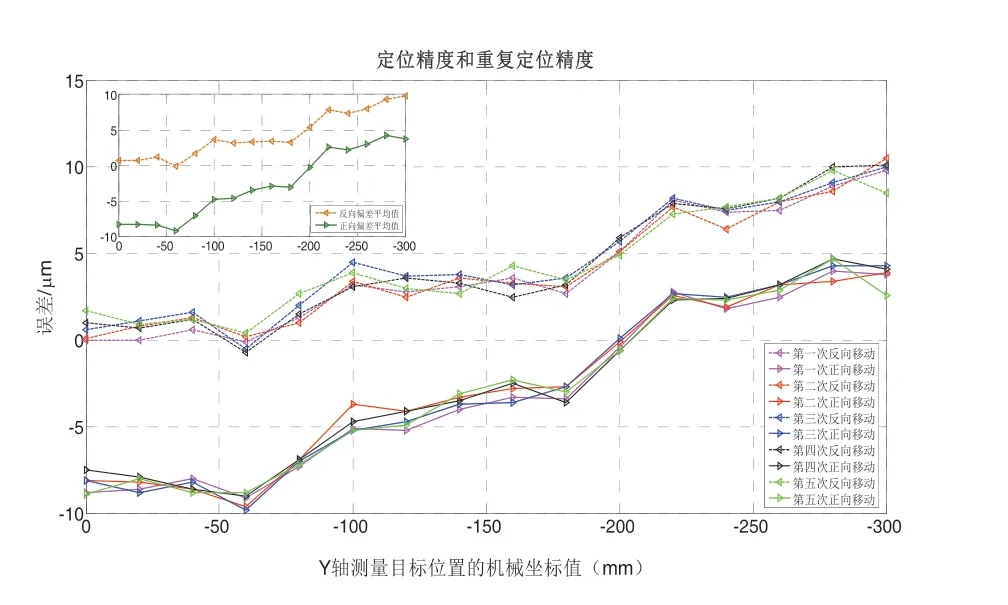
图14 20kg时Y轴定位误差

图15 20kg时Y轴补偿后定位误差

图16 25kg时Y轴定位误差

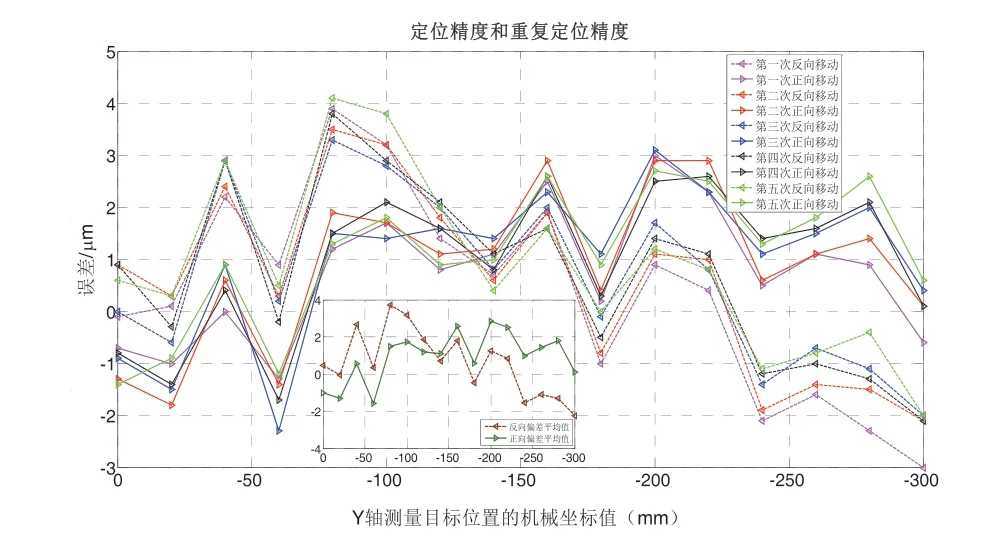
图17 25kg时Y轴补偿后定位误差

由上述曲线图可以看出，经过补偿后的反向间隙大幅度提高，但随着加载重量的不断增大，反向间隙随之不断增大。定位精度和重复定位精度补偿前后的具体变化如表2、表3所示。随着加载重量的不断增大，定位精度有随之不断增大的趋势，但是经过补偿后的定位精度却随着加载重量的不断增大而呈现下降趋势。而重复定位精度却随着加载重量的不断增大而减小，但经过补偿后的重复定位精度有随着加载重量的不断增大而增大的趋势。

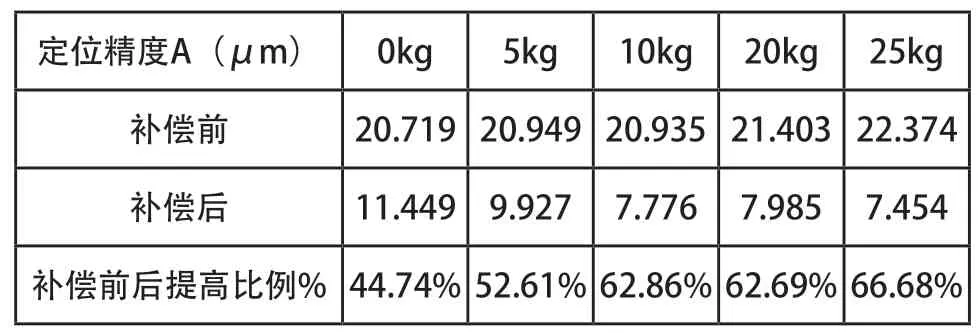
表2 定位精度A补偿前后对比图表

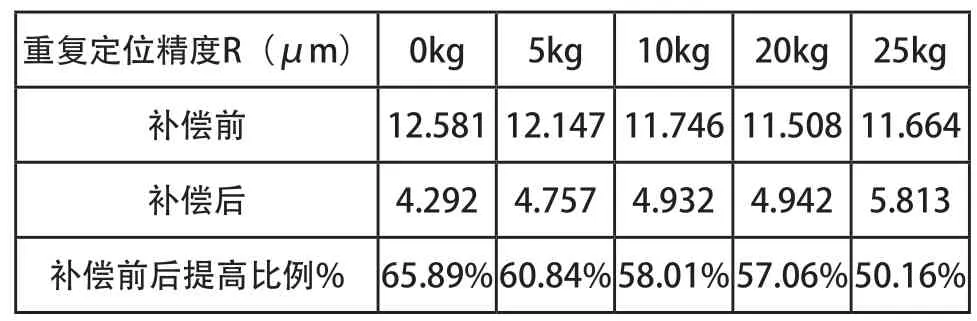
表3 重复定位精度R补偿前后对比图表

5 结语

实验结果表明，经过数控机床单轴受力误差的测量，数控机床的反向间隙随着加载重量的不断增大，反向间隙不断减小，重复定位精度也有一定的减小趋势，但是定位精度有增大的趋势。但经过螺距误差和反向间隙补偿后的反向间隙随着加载重量的不断增大而增大，重复定位精度也有一定的的增大趋势，但是定位精度有减小的趋势。

本文使用激光干涉仪结合一种新的9线误差直接测量方法对数控机床Y轴定位误差的进行测量；而且提出一种数控机床单轴受力的加载方案，以模拟实际切削过程中机床所受的切削力，并测量了数控机床单轴受力条件下的定位误差和计算出了相应的反向间隙，为数控机床在受力条件下的误差测量提供了一定的理论基础，并且为今后数控反向间隙的研究提供了一个新方向。