竖凹槽内螺旋波纹管的沸腾换热与PEC评价

王金锋 滕文强 谢 晶 朱生林 常婉莹

(1.上海海洋大学食品学院，上海 201306；2.上海冷链装备性能与节能评价专业技术服务平台,上海 201306；3.上海水产品加工及贮藏工程技术研究中心,上海 201306；4.上海海洋大学食品科学与工程国家级实验教学示范中心,上海 201306)

能源产业是中国经济的重要支柱产业，设计高效节能的换热设备是实现能源行业可持续发展的重要举措，而螺纹管是被广泛应用的换热设备。其中，两相流的螺纹管被广泛用于食品速冻、牛奶和果汁灭菌等工艺中，尤其是在冷却、速冻、预热、再热、蒸煮加热和废水加热等处理过程中应用较多[1-3]。

目前，螺纹管的研究主要集中在竖凹槽和横螺旋波纹等结构对换热的影响。其中，竖凹槽结构的研究主要是针对制冷剂的沸腾换热特性。王乐乐等[4]研究发现，小管径竖凹槽结构管内干涸现象出现较晚、临界干度较大。戴源德等[5]使用CFD对R290在长度500 mm、外径7 mm换热管中两相流沸腾进行模拟研究，由于换热管内竖凹槽结构存在，工质在管内剧烈扰动。欧阳新萍等[6]研究表明，当流动处于层流或者层流与湍流的过渡区时，较大的螺旋角有利于换热；当流体处于湍流时，较小的螺距会产生较多的螺纹头数，较多的螺纹头数更有利于换热。

针对横螺旋波纹结构主要是研究不同内螺旋波纹结构管的换热特性。Córcoles等[7]研究表明，螺旋波纹高度与内管直径之比最大和螺距与内管直径之比最小时，内管压降最大；螺纹高度与内管直径之比中等和螺距最小时，内管的换热效果最好。陈栩等[8]研究表明小齿高大齿顶角的结构有利于液态制冷剂与壁面形成均匀的液膜，促进管内的换热过程，相同管径下，较多的齿数有利于扰动的增强。刘希祥等[9]研究表明，32°旋转角螺纹管最有利于换热并且压降损失最小。Wang等[10]模拟结果表明内管直径的大小对二次流动的影响很小，表面换热系数和压降均随内管直径的减小而增大。

研究拟通过CFD对不同数量竖凹槽结构的内螺旋波纹管沸腾换热特性进行模拟研究，比较竖凹槽内螺旋波纹结构管的表面换热系数和压降变化，并结合PEC进行评价，以期为竖凹槽内螺旋波纹管优化设计提供依据。

1 数值模拟

1.1 物理模型及网格划分

竖凹槽内螺旋波纹管结构如图1所示，内螺旋波纹管总长度300 mm，内管内径5 mm，管壁0.2 mm，外管内径8.2 mm，内螺纹高度0.3 mm，其中竖凹槽高度与内螺纹高度保持一致，竖凹槽数量为0，4，8，12，14，16，18，20。内管为内螺旋波纹结构，为了更好地对管内的流动沸腾进行捕捉，对内管壁面和外管内壁面进行边界层处理。

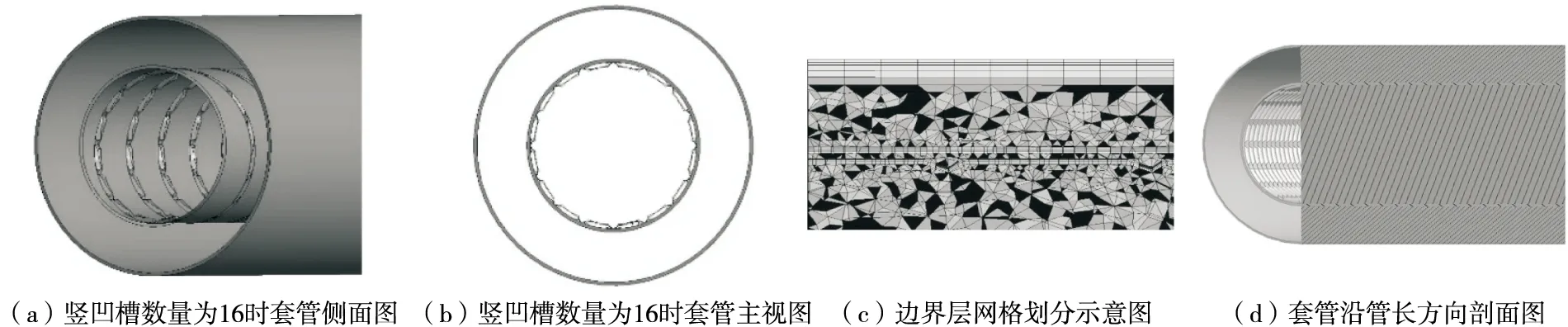
图1 内螺旋波纹管结构Figure 1 Inner spiral bellows structure

1.2 Mixture模型

两相流模型选择Mixture模型，此模型包含连续性方程、动量方程和能量方程。

(1) 连续性方程：

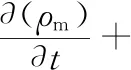
(1)

(2)

(3)

式中：

ρm——混合密度，kg/m3；

αk——第k相体积分数；

ρk——第k相密度，kg/m3；

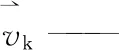
(2) 动量方程：

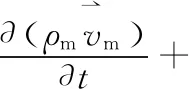
(4)

式中：

βm——体积热膨胀系数。

(5)

(6)

(3) 能量方程：

(7)

式中：

Keff——有效热传导率，W/(m· K)；

SE——所有相的能量源项，J。

第二相体积分数方程：

(8)

相变模型方程：

Senergy=-ML，

(9)

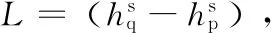
(10)

(11)

(12)

式中：

M——传质速率，mol/(m2·s)；

L——汽化潜热，J/kg；

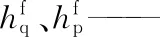
Tref——制冷剂物性的参考温度，℃；

Tsat——制冷剂的饱和温度，℃。

1.3 湍流模型

湍流模型选择RNGk—ε模型，采用标准近壁处理，其包含的方程:

(13)

(14)

式中：

h——表面换热系数，W/(m2·K)；

μ——湍流黏度，Pa·s；

k——湍流脉动动能，J；

Gk——层流速度梯度产生的湍流动能，J；

Gb——浮力产生的湍流动能，J；

ε——湍流脉动动能耗散率；

YM——湍流扩散产生的波动；

C1、C2——常数系数。

1.4 边界条件及算法设置

模型的边界条件和算法设置步骤：

(1) 在两相流Model中将R32的液相设为第1相，R32的气相设为第2相，外管的水设为第3相，并且考虑表面应力的影响，激活Mixture模型中的“implicit body force”选项，沸腾换热模型选择Mixture模型中“Evaporation-Condensation”模型。

(2) 内外管进口均为速度入口，出口均为压力出口，内管为R32液相入口，外管为水入口，其中外管进口水的体积分数为100%，R32和水的流动为顺流。

(3) 内外管壁材料为铜，内外管为耦合边界。

(4) 采用SIMPLE算法，选择Solve N-Phase Volume Fraction Equations，能量方程、体积方程、湍流动能方程均采用一阶迎风方程。

2 结果与讨论

2.1 数值模拟可行性验证

采用Liu and Winterton关联式[11]对数值模拟结果进行验证。沸腾换热分为核态沸腾和膜态沸腾且存在相互作用。根据两种沸腾换热系数的线性加减方式，分别采用膜态沸腾强化因子E和核态沸腾弱化因子S对其进行修正。

h3=[(Eh2)2+(Sh1)2]0.5，

(15)

(16)

(17)

(18)

S=(1+0.055E0.1Re0.16)-1，

(19)

(20)

(21)

式中：

h3——表面换热系数，W/(m2·K)；

λ——流体的导热系数，W/(m· K)；

d——内管的当量直径，m；

M——相对分子质量；

Q——热流密度，W/m2；

ρ——流体密度，kg/m3；

υ——流体速度，m/s；

μ——流体黏度，Pa·s；

Cp——流体的定压比热容，J/(kg ·K)。

模拟值和理论值的比较结果见表1。由表1可知，模拟值与理论值的偏差保持在6%～10%，因此，采用该数值计算模型是可行的。

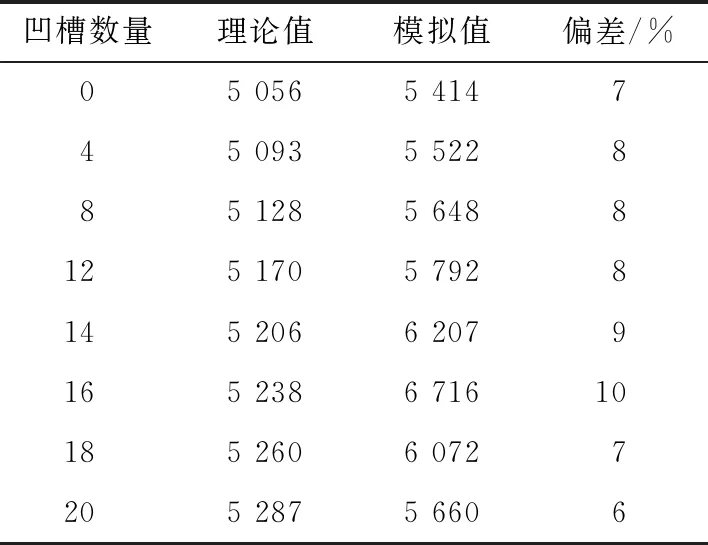
表1 不同数量竖凹槽内螺旋波纹管模拟值与理论值比较Table 1 Comparison of analog value and theoretical value of spiral ripple management in different number of vertical grooves

2.2 表面换热系数

在进行内螺旋波纹管设计时，提高表面换热系数是主要目的。如图2所示，与光管相比，内螺旋波纹管的表面换热系数显著增大(147%)；竖凹槽内螺旋波纹管的表面换热系数随竖凹槽数量的增加先增大后减小，当竖凹槽数量为16时达最大值(157%)；随着竖凹槽数量的进一步增加，表面换热系数逐渐减小，当竖凹槽数量为20时，表面换热系数为光管的154%。

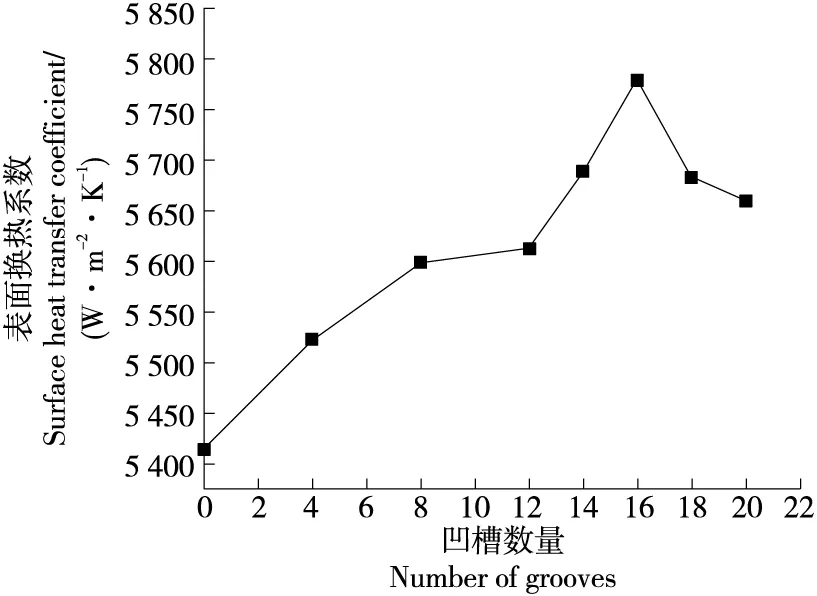
图2 竖凹槽内螺旋波纹管的表面换热系数Figure 2 Surface heat transfer coefficient of inner spiral bellows with different number of vertical grooves

2.2.1 二次流动分析 强化管的换热特性和管内流体流动现象显著相关，内螺旋波纹结构可以强化管内换热，在此基础上，对不同数量竖凹槽内螺旋波纹管内的流动沸腾现象进行研究。如图3中椭圆所指示区域，流体在内螺旋波纹结构下方和侧方产生聚集，这种聚集导致径向二次流动的产生[12]。随着二次流动的产生，湍流动能(TKE)[13]显著增加(如图4所示)，内螺旋波纹结构下方和侧方TKE明显高于其他位置，较高TKE表明此处湍流程度较高，强化沸腾换热强化程度较高。

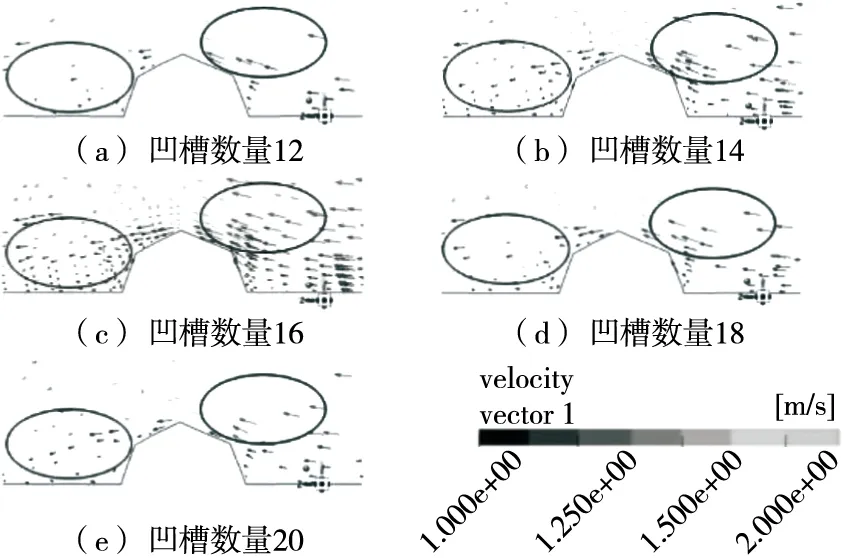
图3 竖凹槽内螺旋波纹管的速度矢量图Figure 3 Velocity vector diagram of spiral bellows in different numbers of vertical grooves

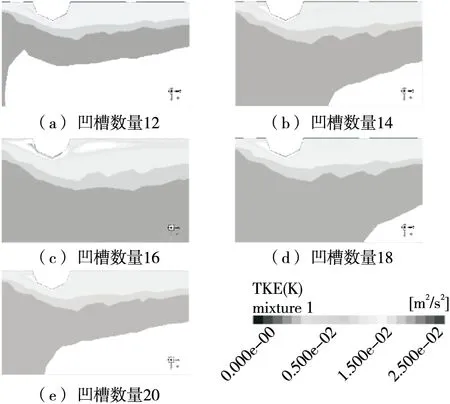
图4 竖凹槽内螺旋波纹管的TKE分布图Figure 4 TKE distribution of spiral bellows in different numbers of vertical grooves

竖凹槽与内螺旋波纹结构相切割，随着竖凹槽数量的增加，内螺旋波纹结构下方和侧方的聚集慢慢增加，径向二次流动逐渐加强，湍流程度得到加强，沸腾换热强化程度越来越高，然而随着竖凹槽数量的进一步增加，聚集慢慢减小，径向二次流动逐渐减弱，湍流程度被减弱。此现象产生的原因是，相邻两竖凹槽间内螺旋波纹结构的弧线长度随竖凹槽数量的增加而逐渐减小(如图5所示)，径向长度随之减小，所以径向二次流动被弱化，沸腾换热被减弱，因此，表面换热系数先增大后减小[14]。

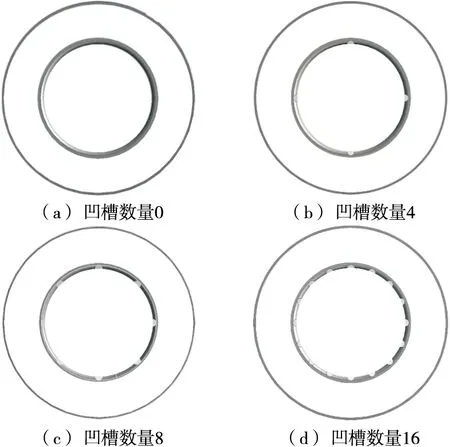
图5 竖凹槽内螺纹波纹管截面图Figure 5 Cross section of internal screw bellows with different number of vertical grooves

2.2.2 内管壁面过热度对气泡的影响 内管壁面的过热度影响内管壁面处气泡的生成与脱离，气泡的生成与脱离又决定内管沸腾换热的强弱。内管(单位长度)中的内螺旋波纹结构增大了换热表面积(如图6所示)，同时在内螺旋波纹结构处的过热度高于光滑壁面，由克劳修斯—克拉贝龙方程[15]可知，内螺纹波纹结构处更容易形成汽化核心，而气泡的生成与脱离又强化了管内沸腾换热。

图6 竖凹槽数量14时内螺旋波纹管中温度分布图Figure 6 Temperature distribution in inner spiral bellows with 14 vertical grooves

竖凹槽与内螺旋波纹结构相切割，换热表面积随之增加，气泡生成和脱离的表面积也随之增加，沸腾换热得到强化。随着竖凹槽数量的进一步增加，内管表面努塞尔数逐渐减小(如表2所示)，内管沸腾换热效果反而降低(如图7所示)，是因为套管结构单位时间内外管进水量相同，热量的传递集中于内螺旋波纹管的内壁面附近，换热表面积的过度增加导致部分内螺纹结构处的温度有所下降(如图8所示)，其过热度低于气泡脱离壁面所需的过热度，气泡无法脱离壁面从而弱化内壁面处沸腾换热，因此，内螺旋波纹管的表面换热系数先增大后减小[16]。

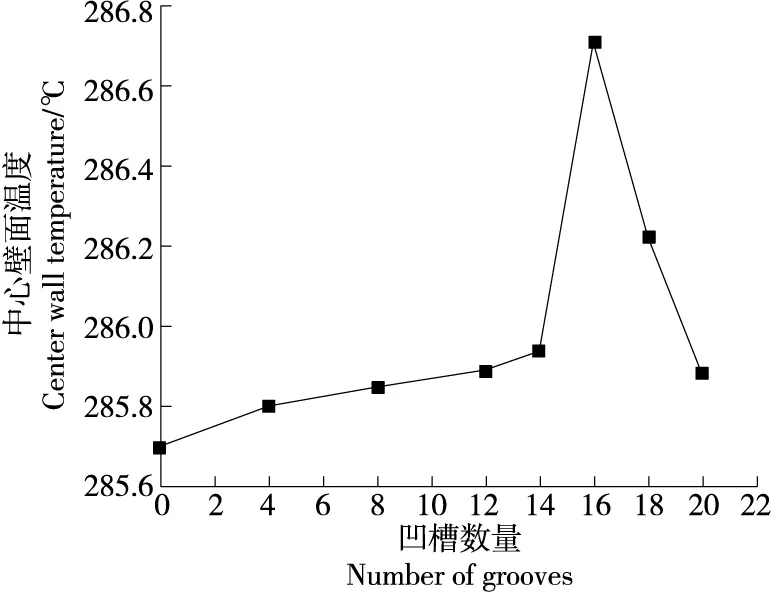
图8 竖凹槽内螺旋波纹管中心壁面温度Figure 8 Central wall temperature of inner spiral bellows with different number of vertical grooves

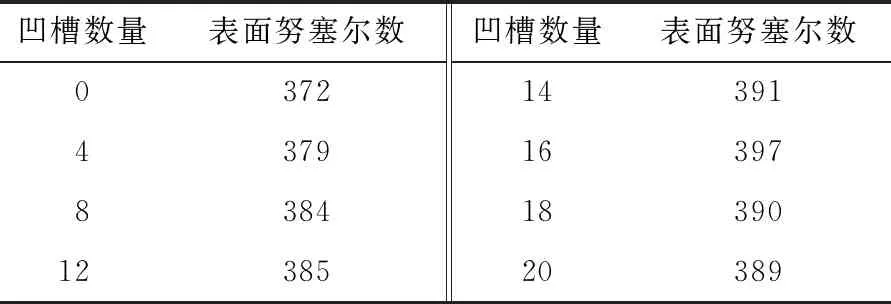
表2 竖凹槽内螺旋波纹管的表面努塞尔数Table 2 Surface Nusselt numbers of spiral bellows in different numbers of vertical grooves

图7 竖凹槽内螺旋波纹管的R32-vapor分布图Figure 7 R32-vapor distribution of spiral bellows in different numbers of vertical grooves

2.3 压降分析

在进行内螺旋波纹管设计时，较高的内管压降会增加压力损失。由图9可知，当竖凹槽数量为0时，内螺旋波纹管压降为光管的221%，内管压降随竖凹槽数量的增加先增大后减小，当竖凹槽数量为16时达最大，为光管压降的261%，竖凹槽数量的进一步增加，内管压降明显下降，当竖凹槽数量20时，内管压降为光管的233%。

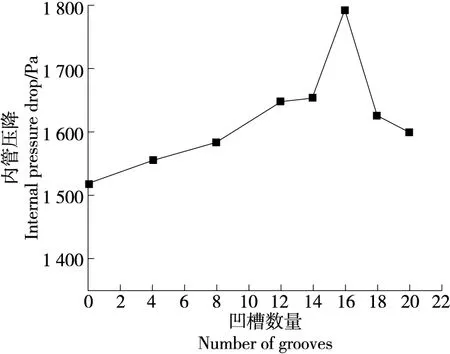
图9 竖凹槽内螺旋波纹管的内管压降Figure 9 Pressure drop of inner spiral bellows with different number of vertical grooves

由图3可知，内螺旋波纹结构增大了内管流体的环流面积，流体在内螺旋波纹管下方的聚集产生了径向二次流动，此外，内螺旋波纹结构侧方有流体聚集(如图3中红色椭圆区域)，增大了内管压降。

竖凹槽与内螺旋波纹结构相切割，随着竖凹槽数量的增加，内螺旋结构下方的聚集慢慢增强，侧方的聚集逐渐形成漩涡(如图3中红色椭圆区域)，内管压降得到增强，当竖凹槽数量为16时，内螺旋波纹管的内管压降增加最迅速，压力最大(如图10所示)。随着竖凹槽数量的进一步增加，相邻竖凹槽间内螺旋波纹结构的弧线长度变短(如图5所示)，聚集效应慢慢减弱，漩涡逐渐消失，湍流流动被破坏，环形流动被减弱，内管压降逐渐下降[17-19]。

图10 竖凹槽内螺旋波纹管的内管压降Figure 10 Pressure drop of inner spiral bellows with different number of vertical grooves

2.4 性能评估

PEC[20]是一种性能评价标准方法，定义为竖凹槽内螺旋波纹管的强化效果与泵功率损耗的比值，其值决定表面换热系数和压降的关系。

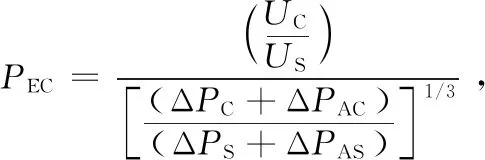
(22)

式中：

PEC——PEC值；

UC——带波纹管的双管热交换器的总传热系数，W/(m2·K)；

US——具有光滑管的双管热交换器的总传热系数，W/(m2·K)；

ΔPC——内波纹管中双管热交换器压降，Pa；

ΔPAC——波纹管一侧的波纹管双管换热器压降，Pa；

ΔPS——内光滑管上的双管热交换器压降，Pa；

ΔPAS——圆环侧带有光滑管的双管热交换器压降，Pa。

表3为不同内螺旋波纹结构下的PEC数值，所有的竖凹槽内螺旋波纹结构中PEC均>1，其中竖凹槽数量为16时，PEC为最大值(1.523)，所以在内管内径5 mm，外管内径8.2 mm，管壁0.2 mm，内螺旋波纹高度0.3 mm，竖凹槽数量为16时，竖凹槽内螺旋波纹管强化换热性能最优。

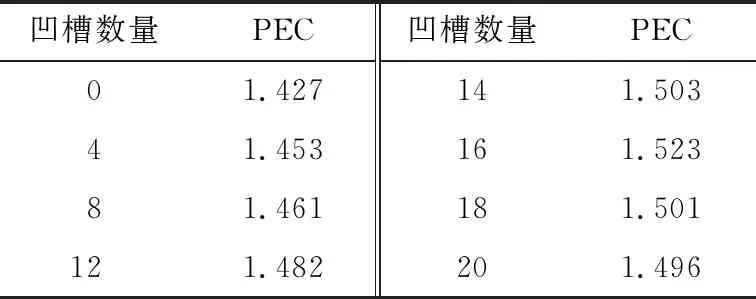
表3 不同竖凹槽数量下内螺旋波纹管的PECTable 3 PEC of inner spiral bellows with different number of grooves

3 结论

以套管结构为设计模型，采用CFD对不同竖凹槽数量的内螺旋波纹管进行沸腾换热模拟研究，分析比较内螺旋波纹管的表面换热系数和内管压降，结合PEC评价，优化竖凹槽内螺旋波纹管结构。结果表明，内螺旋波纹结构增大了内管的换热表面积和环流面积(单位长度)，且产生径向二次流动；表面换热系数和压降分别提高至光管的147%，207%；与内螺旋波纹管相比，竖凹槽内螺旋波纹管表面换热系数和压降均随竖凹槽数量的增加先增大后减小，当竖凹槽数量为16时达到最大值，分别为内螺旋波纹管的107%，118%；此外，当竖凹槽数量为16时，PEC最大(1.523)，此时换热管的综合性能最优。在内(外)管内径分别为5.0，8.2 mm，内(外)管壁厚度为0.2 mm 和内螺纹高度0.3 mm下，竖凹槽数量为16的竖凹槽内螺旋波纹管的换热性能最佳，但是不同管径下竖凹槽内螺旋波纹管性能最优化结构以及竖凹槽与竖凹槽内螺旋波纹管的性能关系还有待进一步研究。