基于蝙蝠算法优化支持向量机的滚动轴承故障诊断

罗源睿 王海瑞

（昆明理工大学信息工程与自动化学院）

滚动轴承在电力、冶金及航空等领域的应用非常广泛，尤其是在旋转机械设备上，是不可或缺的部件之一。然而大多数机械设备发生故障都与滚动轴承密切相关，因此对滚动轴承的故障诊断研究具有十分重要的意义［1］。

由于滚动轴承是最易损的部件之一，且出现故障时的振动信号多呈现非线性、非平稳性［2］。因此Wu Z H等提出了集成经验模式分解（Ensemble Empirical Mode Decomposition，EEMD）方法［3，4］，通过在每次信号分解的过程中添加高斯白噪声，在有效滤除噪声影响的同时也解决了分解中存在的模态混叠现象。

支持向量机（Support Vector Machines，SVM）在故障诊断方面的应用很广泛，对于解决小样本、非线性及高维特征等问题具有很好的识别能力［5，6］。但SVM中核函数参数σ和惩罚参数C往往依靠人为经验来选取，其值的大小对SVM的识别准确率尤为重要。近年来，群智能算法在优化SVM参数方面取得了很大的进展，其中蚁群算法［7］、遗 传算法［8］及 粒子群 算 法［9，10］等 应 用 广 泛。笔者采用蝙蝠算法［11］（Bat Algorithm，BA）来优化SVM参数，实验结果证明了该方法能获得更高的识别率和较好的性能。

1 EEMD

1.1 EEMD的基本原理

EEMD是在经验模式分解（Empirical Mode Decomposition，EMD）的基础上改进得到的［12］。通过在EMD分解信号中加入高斯白噪声并进行多次分解求均值，使信号在不同尺度上具有连续性，不仅能有效滤除噪声对信号的影响，还抑制了EMD分解中存在的模态混叠现象［13］，具体步骤如下：

a.首先在原始信号x（t）中多次加入高斯白噪声ni（t），则第i次加入高斯白噪声后的信号xi（t）=x（t）+ni（t）；

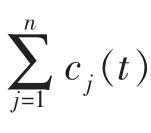
通过EEMD分解可将任意非线性、非平稳的信号分解成若干个模态函数分量IMF和一个残余分量。各个IMF分量代表了信号在不同频率范围内所包含的成分，不同的信号不同频率范围内所包含的成分不同，能量分布也不同。图1、2分别为采集到的滚动轴承内圈故障振动信号和该振动信号EEMD分解后的结果，可以看出分解得到了12个IMF分量和1个残余分量。

图1 内圈故障振动信号

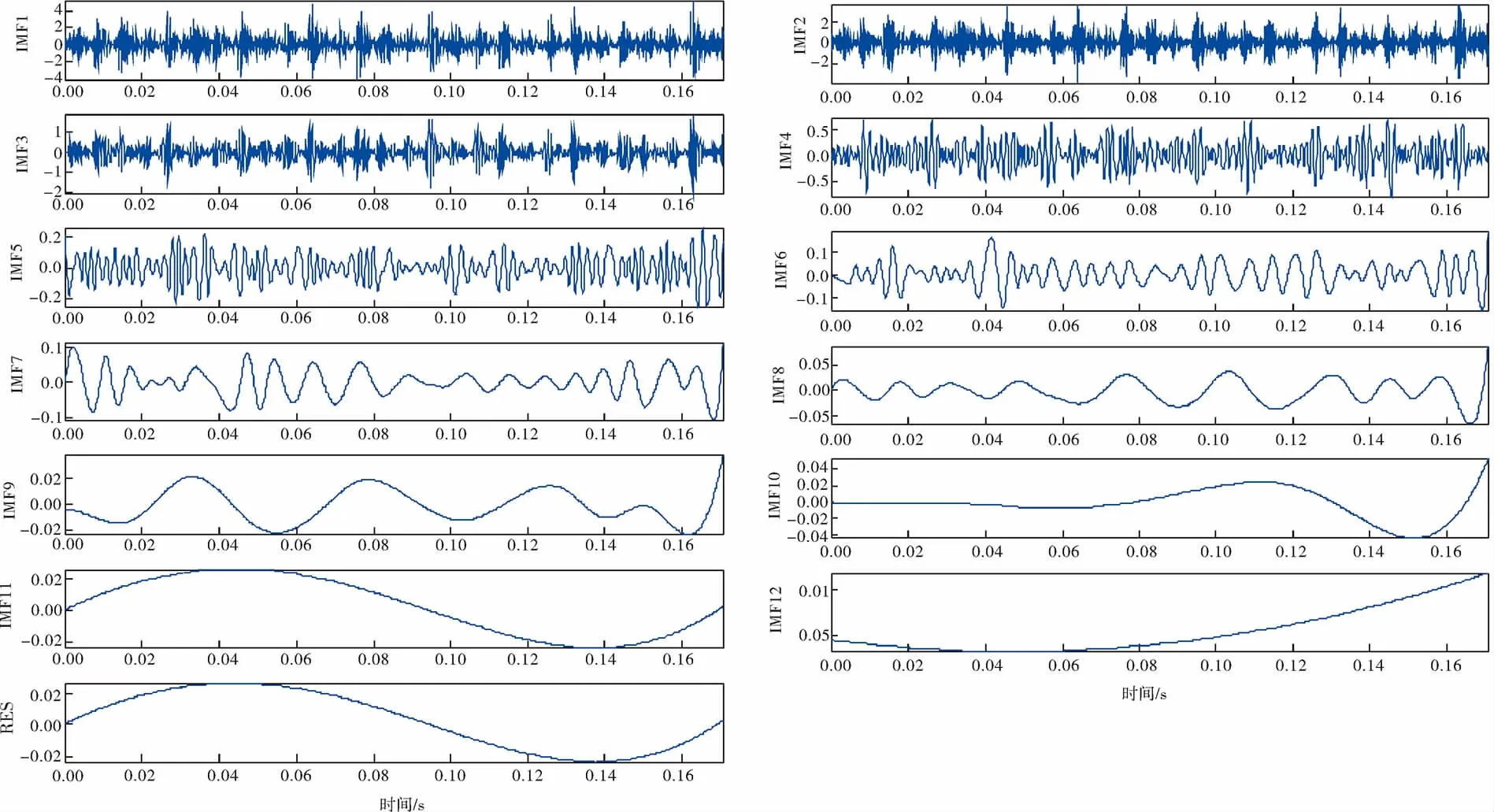
图2 内圈故障振动信号EEMD分解后的结果

1.2 EEMD能量熵

滚动轴承在不同状态下采集到的振动信号不同，其各频率分量和能量分布也会随着振动信号的改变而改变［14］，因此可以根据其能量值判断滚动轴承的工作状态。

通过计算EEMD分解振动信号x（t）后，得到n个IMF分量相应的能量E1，E2，…，En，从而获得信号中的能量分布，即能量熵。在忽略残余分量的情况下，各个IMF分量的能量之和等于原信号的总能量。由于IMF的各分量c1，c2，…，cn包含不同的频率成分，且各分量具有的能量也不相同，从而形成了信号在频域的能量分布，则EEMD能量熵HEn可定义为：

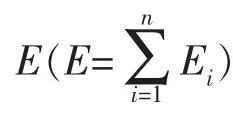
滚动轴承在不同工作状态下振动信号的能量熵值如下：

正常状态 1.248 4

内圈故障 1.066 6

滚动体故障 0.919 7

外圈故障 0.769 8

从以上数据可以看出，不同状态下的能量熵值不同，正常状态下的能量熵值最大，这是因为滚动轴承在正常状态下，信号相对平稳，故能量分布较均匀、不确定性较高。当轴承发生故障时，会导致能量在一定的频率范围内集中，不确定性减少，使能量熵值也随着变小。因此可以将能量熵作为后续输入BA-SVM模型的特征向量，这样能更客观地反映轴承的状态，更好地对轴承不同故障类型进行诊断。

2 蝙蝠算法

蝙蝠算法是通过模拟蝙蝠捕食过程和躲避障碍物而演变的搜索算法，具有很好的全局寻优能力和较快的收敛速度［15］。首先蝙蝠利用声呐系统发出超声波脉冲，再通过遇到猎物或障碍物时反射回来的声波信号进行判断，并及时调整飞行方向和速度，最终有效地避开障碍物并快速捕食猎物。

假设蝙蝠算法的搜索空间为d维，蝙蝠i在寻优过程中脉冲频率fi、速度vi和位置yi在t时刻的更新公式如下：

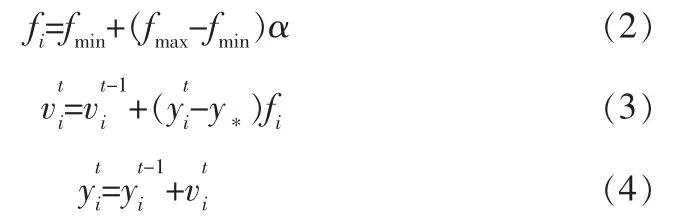
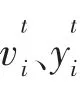
为了确保算法的局部搜索能力，从当前最优解中随机选取一个解并对之施加一个随机扰动，然后在该解的附近进行搜索，在局部搜索阶段相应的位置更新公式为：

其中，ε表示一个随机数且ε∈［-1，1］；yold表示随机选取的一个位置最优解；At表示全部蝙蝠个体在t时刻的脉冲响度均值。

在蝙蝠搜索过程中，通过判断猎物与其自身的距离，并以此为据对脉冲频度ri和响度Ai进行更新。当蝙蝠距离猎物较近时响度会逐渐降低，声波的发射频度会逐渐提高，更新公式为：

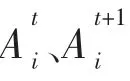
3 基于BA算法优化的支持向量机

支持向量机是一种二分类模型，核函数参数σ和惩罚参数C作为SVM中最重要的两个参数，分别影响了SVM算法的分类识别率和泛化能力。而SVM参数往往依靠人为经验选取，影响其分类性能。目前对参数σ和C的优化算法有很多，比如蚁群算法、遗传算法及粒子群算法等，但这些算法都存在易陷入局部最优、收敛能力弱等缺点，从而导致分类结果不理想。

针对上述存在的问题，笔者提出了基于蝙蝠算法优化支持向量机的滚动轴承故障诊断模型。利用BA很好的全局寻优能力和收敛速度对SVM参数进行优化选择，从而获得最优参数组合（C，σ），提高了SVM的分类识别率和速度，其优化流程如图3所示。

图3 BA-SVM优化流程

4 实验与结果分析

4.1 样本选择与特征提取

笔者采用美国凯斯西储大学轴承数据中心的滚动轴承数据。实验用加速度传感器对信号进行采集，分别采集了轴承在正常状态、内圈故障、滚动体故障和外圈故障4种状态下的振动信号。分别在每种状态下选取20组振动信号数据，随机选取其中的15组作为训练样本，剩余的5组作为测试样本。首先对训练样本进行EEMD分解，选取分解后的前8个故障信息丰富的IMF分量，再计算各分量对应的能量并构成特征向量，并将之输入到多故障分类器中进行训练，训练样本的能量特征向量见表1（由于篇幅有限，每种状态只列举了部分样本，且保留4位有效数字），最后利用测试样本对训练好的分类器进行轴承工作状态的测试。

表1 部分训练样本的能量特征向量

4.2 建模与诊断

利用BA对SVM的参数进行寻优，BA的迭代次数为200、种群规模为20，BA-SVM的最佳适应度曲线如图4所示。当最佳适应度曲线稳定时，代表已趋于收敛，即获得最佳参数组合，从图4中可以看出，迭代次数为第4代时就趋于平稳。

为了验证BA-SVM模型对滚动轴承故障诊断的效果，与GA-SVM、PSO-SVM诊断模型进行比较，结果如图5所示。可以看出，BA-SVM经过少量迭代即迅速搜索到最优值，相较于GA-SVM和PSO-SVM而言，收敛精度高且寻优速度快。

图4 BA-SVM的最佳适应度曲线

图5 3种模型的最佳适应度曲线

从算法运行时间上分析上述3种故障诊断模型的性能，从表2可以看出，BA-SVM相对于GASVM和PSO-SVM而言，在运行时间和故障诊断识别率方面都有较大的优势，由此也证明了BASVM模型在滚动轴承故障诊断方面的有效性和稳定性。

表2 3种模型性能比较

5 结束语

针对支持向量机中参数选取不当易影响分类结果的问题，笔者采用蝙蝠算法优化支持向量机参数，并应用于滚动轴承的故障诊断中。实验结果表明BA-SVM模型相较于GA-SVM和PSOSVM模型而言，诊断识别率高、收敛速度快，对滚动轴承故障诊断效果较好。因此笔者所设计的BA-SVM模型能够有效识别滚动轴承在运行中发生的多类故障，保障了滚动轴承的有效运行，具有较高的应用价值和广阔的应用前景。