热风炉拱顶温度模糊自适应滑模控制策略

冯旭刚,鲍立昌,章家岩,王兵,魏新园,王胜,魏舜昊,徐帅,陈雨薇

(安徽工业大学电气与信息工程学院,243032,安徽马鞍山)

热风炉使用的燃料是炼铁生产过程中产生的高炉煤气,其压力和热值波动较大,故造成拱顶温度难以控制稳定[1]。高风温技术是钢铁企业实现高炉节能的关键技术之一,然而若要提高高炉热风炉送风温度,就必须同步提高热风炉的拱顶温度[2-3]。因此,合理控制拱顶温度,对于保证高炉设备的安全稳定运行,提高企业经济效益具有重要意义。

工程上,针对热风炉拱顶温度通常采用常规的PID控制方法,难以达到理想的控制效果。为此,国内外专家学者针对拱顶温度控制进行了多种先进控制策略的研究。文献[4]提出数学模型控制法,基于热风炉炉内热平衡建立数学模型,较好地反应了热风炉燃烧过程中的变化情况。由于该方法需要在现场安装众多高精度检测装置来获取热风炉的状态信息,且这些装置的运行状况对数学模型的推导和数值演算有直接影响,因此该方法仍存在一定程度的局限性和不足。文献[5]提出了一种基于RBF神经网络整定的PID控制策略,在常规热风炉温控系统的基础上,通过改进串级控制实现热风炉的燃烧优化调整,将外环改为采用RBF神经网络整定的PID控制,通过RBF神经网络算法对增量式PID参数进行调整。由于RBF神经网络易陷入局部极小值,且径向基层与输出层之间的联接权求解存在病态问题,易造成控制参数整定错误。文献[6]在考虑炉内压力变化的基础上建立了外燃式热风炉烧炉过程的三维模型,模型考虑了蓄热砖区域内燃料与空气的湍流混合物、燃烧反应、浮力对流、热辐射和热交换,然后将计算结果与实际测量数据进行比较,以验证所提数学模型的准确性和可用性。所建模型的求解结果为热风炉烧炉末期的温度场分布情况,仅能为热风炉的工艺结构设计提供指导,对热风炉燃烧过程的实时调控意义不大。文献[7]以热风炉拱顶温度为被控对象,根据非参数预估原理,设计出一种应用于拱顶温度预估补偿环节的非参数在线预估器,组成具有非参数在线预估器的模糊控制系统。但是,预估器所需设置参数众多且计算方式复杂,不利应用于工程实际。

本文提出了一种拱顶温度模糊自适应滑模控制策略,借助模糊控制的万能逼近特性,实现热风炉拱顶温度模型未知部分的自适应逼近,有效降低了模糊增益。通过反馈校正技术,利用拱顶温度跟踪误差,实时更正模型参数,抑制拱顶温度在调节过程中的超调和滑模抖振,从而达到有效提高拱顶温度控制系统抑制扰动能力的目的。

1 拱顶温度控制系统特性

拱顶温度是表征热风炉运行状态的重要参数,关系到热风炉的安全稳定运行,是衡量燃料流量与助燃空气流量是否匹配的重要标志[8-9]。热风炉燃烧控制的主要任务是保证拱顶温度快速达到设定值并维持稳定,当拱顶温度过高时,为避免烧损热风炉炉底结构部件,应在减小燃料量的同时增大助燃空气流量。当拱顶温度过低时,为提高热风温度,应同时增大燃料量和助燃空气流量。在保证拱顶温度稳定的情况下,以此来调节空燃比提高废烟气的温升速率,保证热风炉经济高效运行[10-13]。

由文献[15]可知,热风炉拱顶温度模型可表示为

(1)

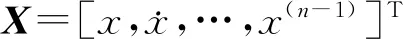
2 拱顶温度控制策略设计

图1 拱顶温度模糊自适应滑模控制框图Fig.1 Block diagram of fuzzy adaptive sliding mode control of vault temperature

2.1 滑模变结构控制策略

在实际控制系统中,由于外部干扰的上界很难确定,且系统参数f(X,t)和g(X,t)往往未知。所以在常规滑模控制中,常给定一个较大的上界值来确保系统的稳定性,但这会造成系统控制律过大,进而导致系统抖振剧烈[9,15]。本文采用如下方法解决这一难题,设

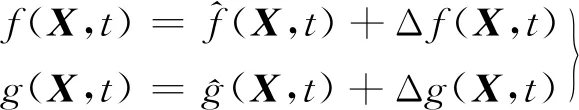
(2)

(3)

式中:ω=Δf(X,t)+Δg(X,t)u+d(t)为系统不确定项总和。

拱顶温度控制系统的控制目标是当系统存在外部干扰和模型不确定项的情况下,设计控制律使拱顶温度实际输出y跟随期望输出yd。

定义跟踪误差为

e=yd-y=xd-x

(4)

定义切换函数为

s(e)=CTe

(5)

根据以上推导,等效控制项为

(6)

在实际控制过程中,由于系统存在不确定项和外部干扰,系统状态会偏离滑模面,因此有必要引入附加控制项,使系统轨迹在有限时间内趋向滑模面。附加控制项设为

(7)

那么,最终选取的拱顶温度控制律为

u=ueq+un

(8)

2.2 模糊自适应滑模控制策略

为进一步降低抖振,提高系统自适应能力和响应速度,抵消由建模误差和外部扰动对系统的影响,设计模糊自适应控制器,估计未知非线性函数和系统总的不确定项。

定义模糊逼近调节规则如表1所示。

表1 模糊逼近调节规则表Table 1 Fuzzy approximation adjustment rule table

采用乘积推理机、单值模糊器和重心法将模糊变量反解出来,得到模糊控制器的输出为

θTξ(x)

(9)

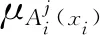
(10)

(11)

定义最小逼近误差为

(12)

定义最优参数向量为

(13)

式中:Ωf、Ωg和Ωω分别是θf、θg和θω的集合。

由此,拱顶温度控制律变为

(14)

对控制器稳定性进行Lyapunov分析,则

(15)

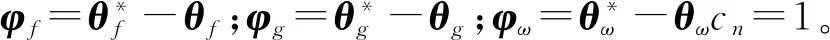
定义Lyapunov函数

(16)

则

(17)

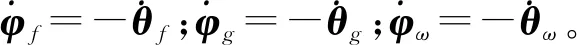
由模糊控制理论可知,模糊控制可以在紧密集上以任意精度逼近任意连续函数。由于模糊规则的限制,导致实际工程应用中模糊控制会产生较大误差[16-18]。因此,本文需要在模糊控制的基础上引入自适应控制律对自适应系数r1、r2和r3进行优化,使模糊系统输出随着拱顶温度变化进行实时调节,从而使控制律更加精确。

由式(17)可知,自适应律应选择为

(18)

将自适应律式(18)代入式(17),得

(19)

3 仿真分析

(20)

(1)为检验控制算法的模糊逼近能力,对模型未知参数和不确定项模糊逼近仿真,仿真结果如图2～5所示。

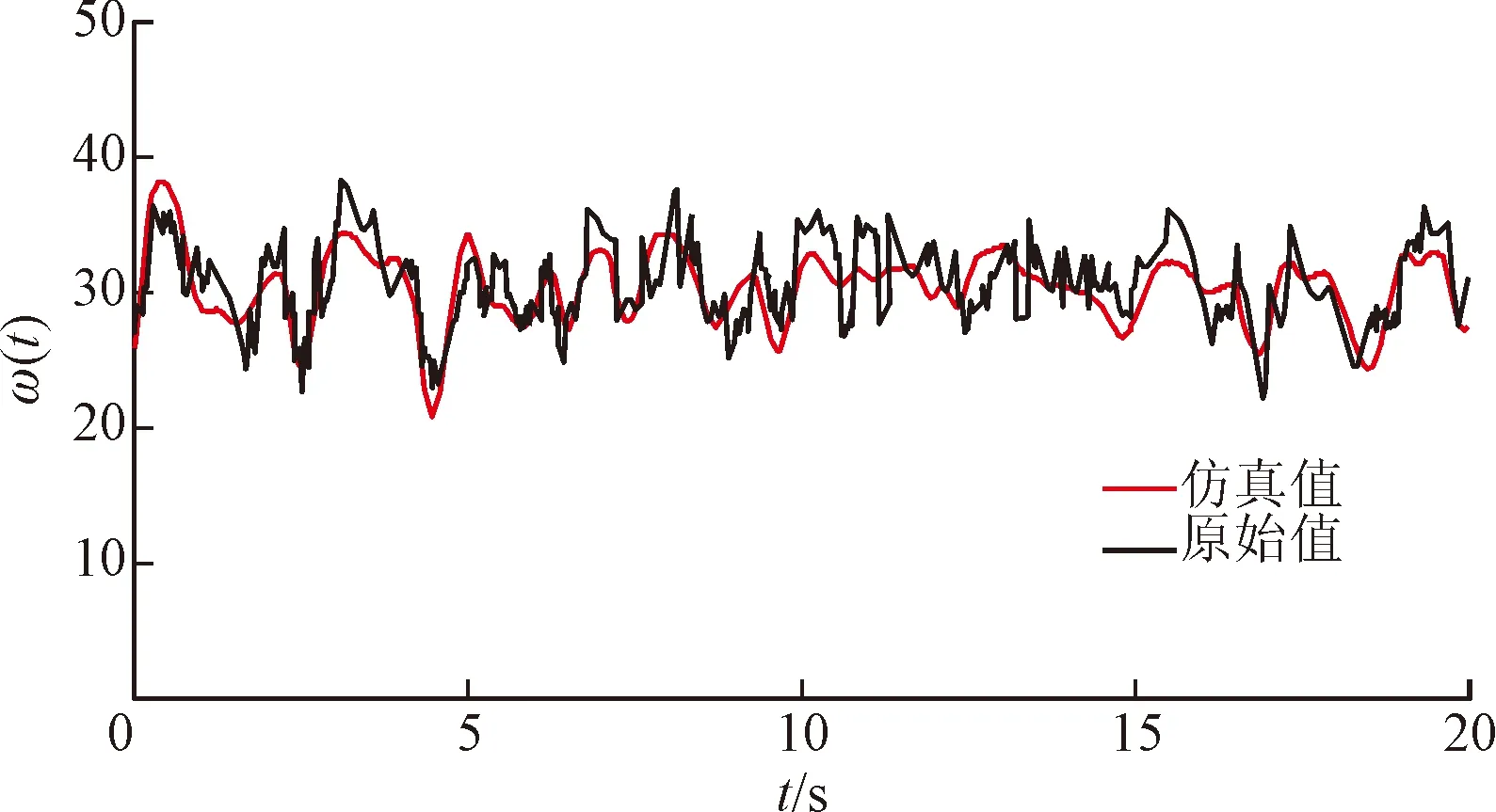
图2 模型不确定项ω(t)模糊逼近仿真Fig.2 Fuzzy approximation simulation of model uncertainty ω(t)

图3 模型不确定项ω(t)模糊逼近误差Fig.3 Fuzzy approximation error of model uncertainty ω(t)

图模糊逼近仿真Fig.4 Fuzzy approximation simulation of

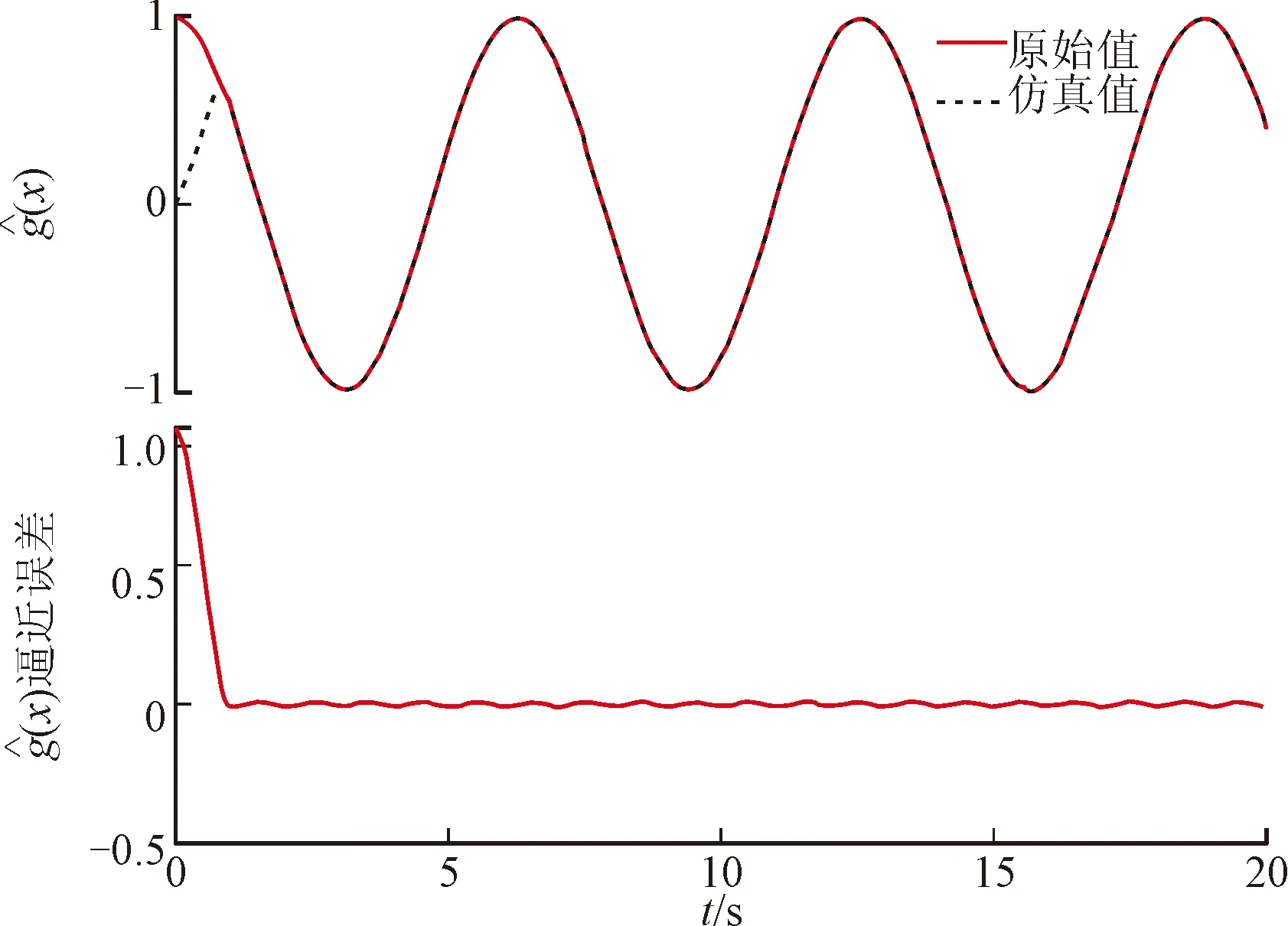
图模糊逼近仿真Fig.5 Fuzzy approximation simulation of

由图2～图5可知,模糊自适应滑模算法对系统不确定项、未知函数和未知控制增益具有良好的跟随逼近能力,不确定项逼近误差小于±4,连续函数f(x)的逼近误差小于±0.01,控制增益g(x)的逼近误差小于±0.04,可见模糊自适应滑模控制能够得到较为精确的对象模型参数。

(2)为验证控制算法的抗干扰性能,同时对PID控制、常规滑模控制和本文提出的模糊自适应滑模控制施加阶跃信号。拱顶温度设定值为1 200 ℃,并在运行45 s时加入幅值为20%的阶跃干扰,观察抗干扰效果和输出变化情况。仿真结果如图6和图7所示。

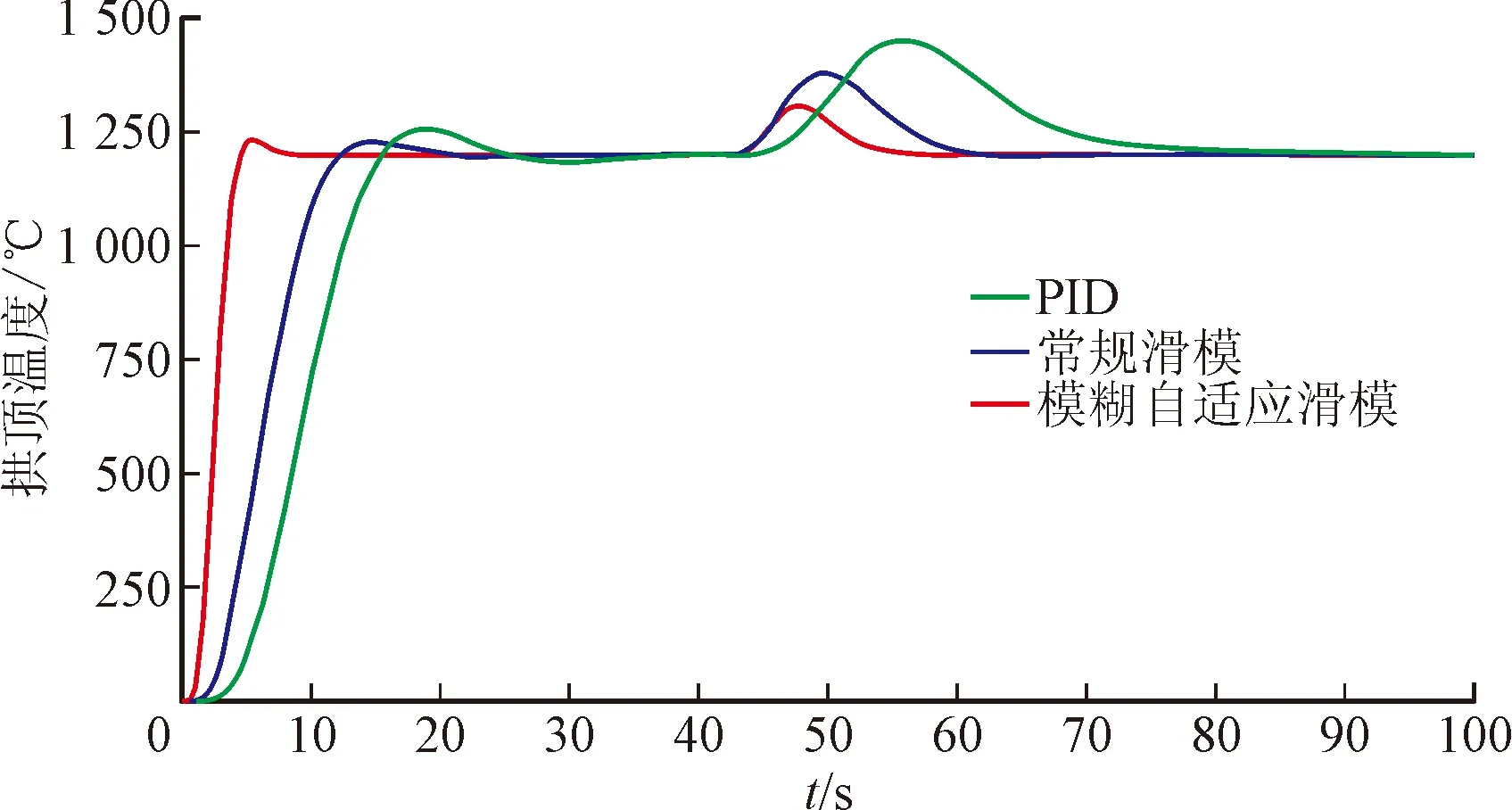
图6 拱顶温度阶跃响应对比图Fig.6 Comparison of vault temperature step responses

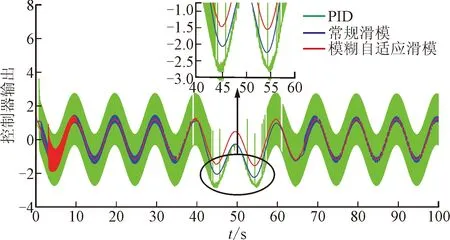
图7 控制器输出对比图Fig.7 Controller output comparison

由图6可知,常规PID控制的稳定时间为40 s,常规滑模控制的稳定时间为22 s,模糊自适应滑模的稳定时间为9.2 s。当加入20%的阶跃干扰后,常规PID控制的调节时间为46 s,超调量为20.9%,常规滑模控制的调节时间为19 s,超调量为14.8%,模糊自适应滑模的调节时间为11 s,超调量为8.8%。由图7可知,在加入干扰后,模糊自适应滑模控制器的输出抖振、常规滑模控制器输出抖振和PID控制器输出抖振相比分别降低了16%和37.5%。由此可见,模糊自适应滑模控制策略相比常规滑模和PID控制策略的抗干扰能力更好,并能够在消除抖振的同时获得较快的响应速度,取得更好的控制效果。

(3)为进一步验证模糊自适应滑模控制策略的跟随性能和鲁棒性能,向系统施加sin(πt)的连续干扰信号,设定信号为yd=200sin(0.033πt)+1 200,仿真结果如图8所示。

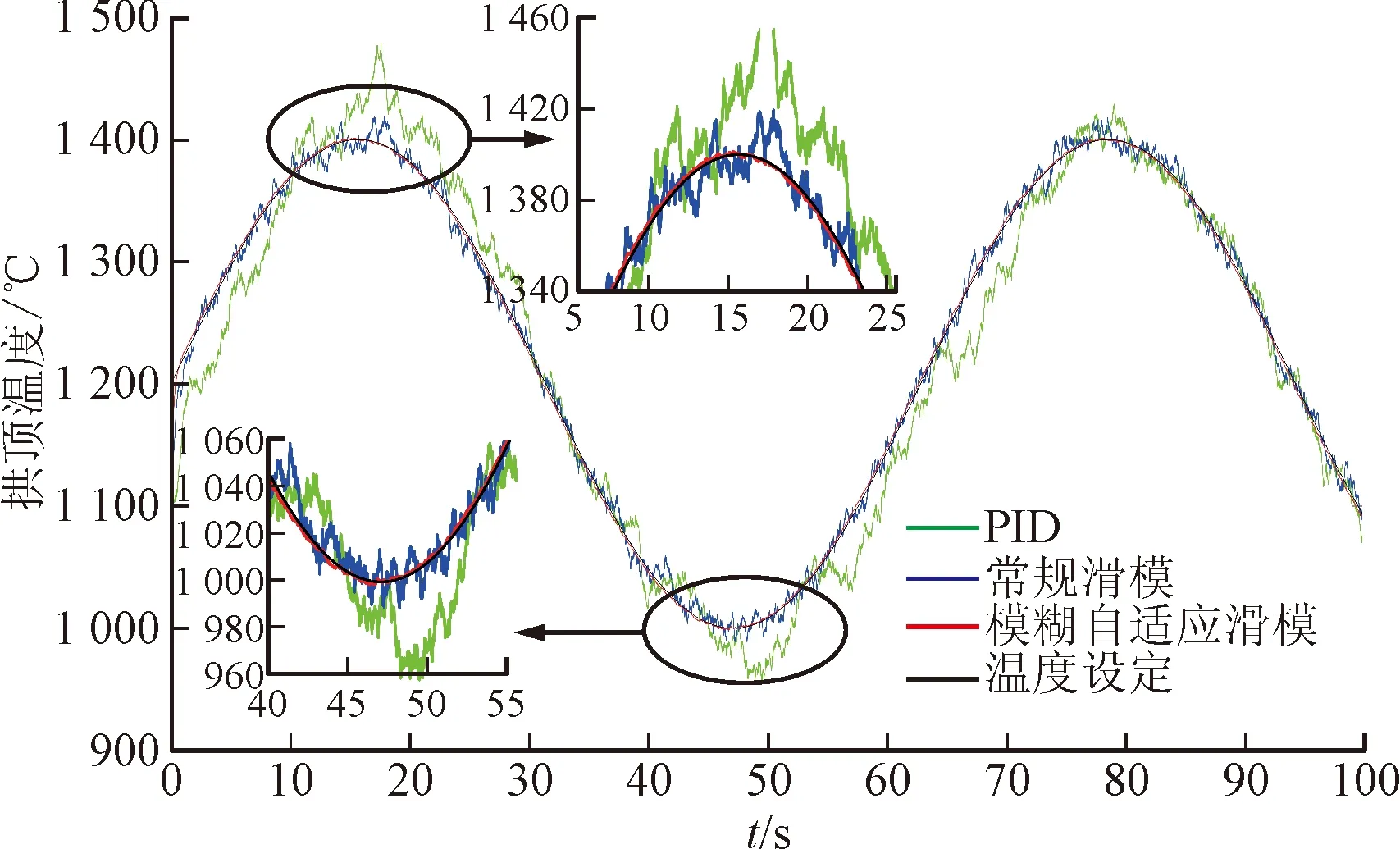
图8 跟随性能仿真对比图Fig.8 Following performance simulation comparison

由图8可知,在相同的干扰信号下,模糊自适应滑模控制策略的跟踪误差在±3 ℃之间,常规滑模控制策略的跟踪误差在±19 ℃之间,PID控制策略的跟踪误差在±64 ℃之间。对比3种控制策略可知,在连续扰动下,模糊自适应滑模控制策略的收敛性更好,位置跟随误差更小,鲁棒性更强。表明本文设计的模糊自适应滑模控制策略可以很好地实现对热风炉拱顶温度外部干扰的自适应逼近,从而提升拱顶温度的控制精度。

4 工程应用

为检验模糊自适应滑模控制策略的有效性,本文以某炼铁厂2 060 m3高炉配套的4座顶燃式热风炉拱顶温度为对象进行工程应用。采用本文的控制策略,控制系统为施耐德PLC,在不改变原系统结构和硬件配置情况下,增加一套由燃烧优化控制器和监控计算机组成的热风炉拱顶温度优化控制系统。监控计算机与优化控制器之间通过工业以太网采用OPC协议进行数据通讯,而优化控制器与现有PLC系统操作员站则通过OPC协议进行联接和信息传输。现场的PLC系统由I/O设备及检测元件、变送器、驱动放大器、调节阀和传动设备组成,担负现场各种传感器信号的采集、处理和调节阀的实时控制,监控计算机承担数据库建立、数模计算、能效分析、集中监视、局部操作和系统设置、参数修改等工作。优化控制器主要完成数据传输、优化计算、控制指令下载和无扰切换等任务。系统具体架构如图9所示。

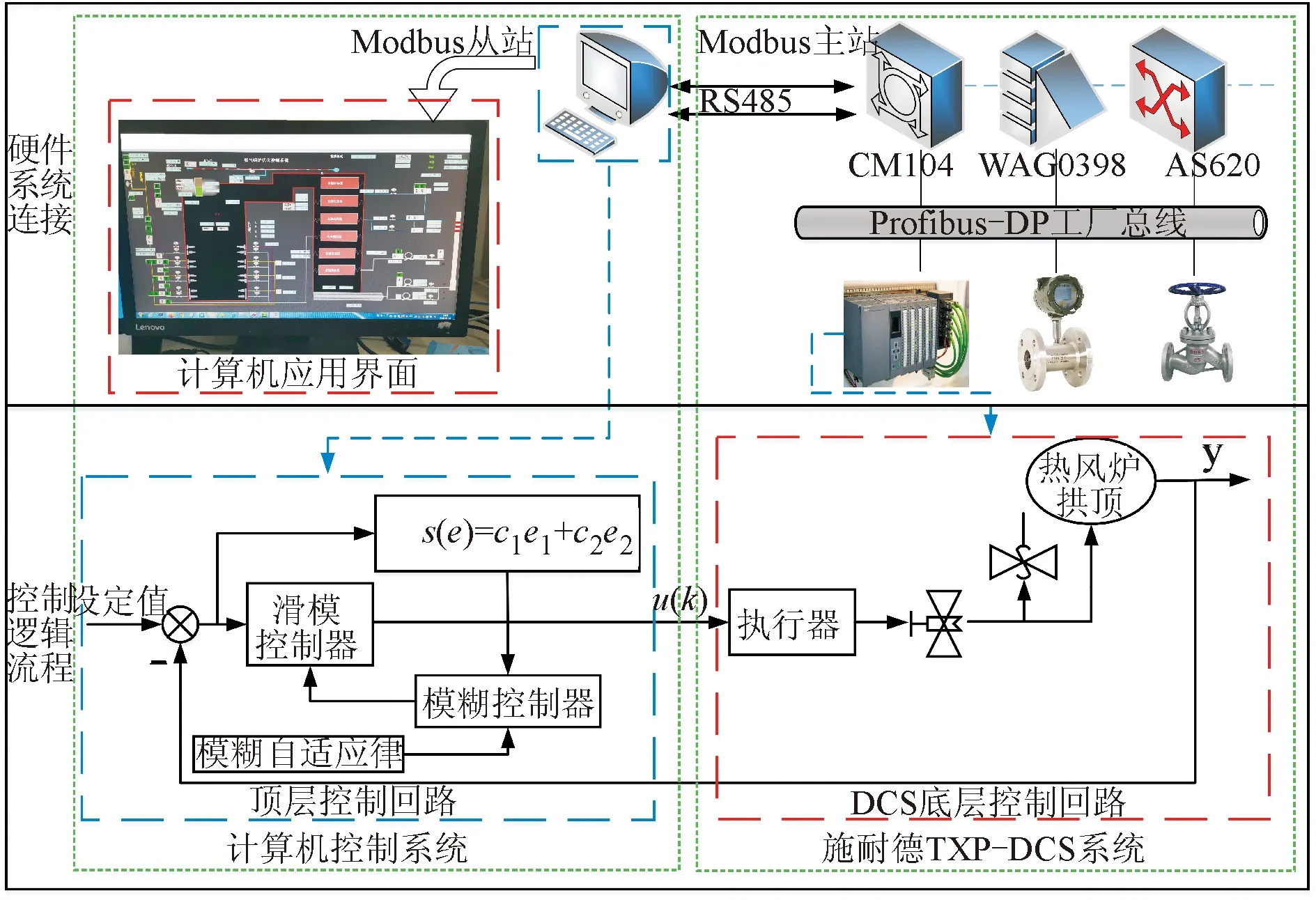
图9 拱顶温度优化控制架构Fig.9 Vault temperature optimization control architecture

本文将拱顶温度模糊自适应滑模控制策略投入现场运行控制,并通过反复调试,取得了良好的控制效果。热风炉在额定负荷下连续3 d分别采用常规PID控制、滑模控制和模糊自适应滑模控制的拱顶温度见图10～图12,拱顶温度设定值为1 200 ℃,监测时间为8 h。

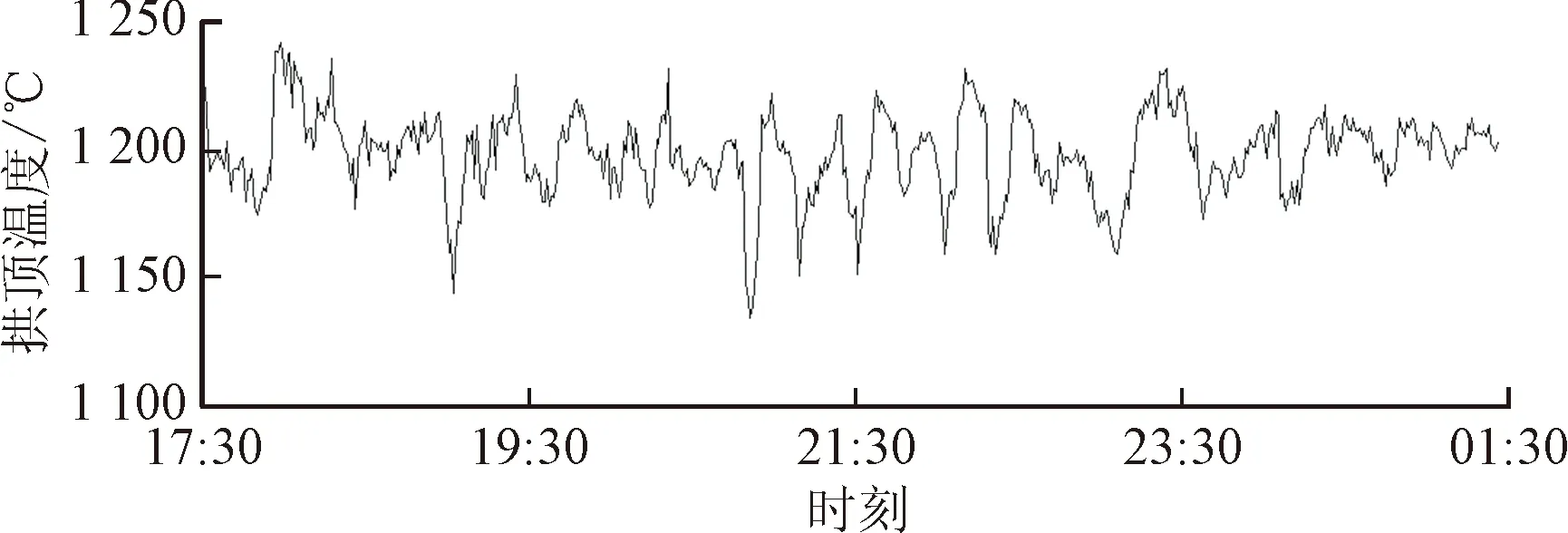
图10 PID控制策略拱顶温度实时曲线Fig.10 Vault temperature real-time curve from PID control strategy

图11 常规滑模控制策略拱顶温度实时曲线Fig.11 Real-time curve of vault temperature from conventional sliding mode control strategy

图12 模糊自适应滑模控制策略拱顶温度实时曲线Fig.12 Real-time curve of vault temperature based on fuzzy adaptive sliding mode control strategy

由图10～图12可知,当热风炉拱顶温度控制系统采用本文的模糊自适应滑模控制策略时,温度波动平缓且波动范围在±5 ℃以内,而采用常规滑模和PID控制策略时,温度波动剧烈且波动范围分别为±23 ℃和±70 ℃。由此可见,本文提出的模糊自适应滑模控制策略达到了良好的控制效果。

5 结 论

热风炉拱顶温度控制系统具有大惯性、超调大和纯滞后等特点,且在运行过程中易受外界干扰。鉴于常规控制方法对于拱顶温度控制无法达到较好的效果,本文提出了一种基于模糊自适应滑模控制的拱顶温度控制策略,利用模糊自适应滑模控制器补偿系统不确定扰动因素和逼近误差,从而修正位置跟踪的稳态误差,提升系统的鲁棒性。与PID和常规滑模控制策略相比,模糊自适应滑模控制策略减小了系统抖振,使控制系统具有更优越的控制精度、响应速度和稳态性能。最后,将本文控制策略应用于某炼铁厂高炉热风炉,应用结果表明,拱顶温度控制偏差在±5 ℃以内,有效地提高了热风炉拱顶温度控制系统的稳定性。