基于相关熵的快速聚类算法

李中衡,杨奔,张劲节,刘银川,张雪涛,王飞

(西安交通大学视觉信息处理与应用国家工程实验室,710049,西安)

聚类[1-13]也称为无监督学习,可以将无标签数据自动划分为确定的类别,广泛应用于数据挖掘[14]、计算机视觉[15]和模式识别[16]等领域。早期聚类算法研究的热点是如何提高聚类的性能,针对这一问题,研究人员提出了许多聚类算法,如基于矩阵分解的算法[11,12,17-19]、基于k均值的算法[1-3,13,20]以及基于谱聚类(SC)的算法[4-6,15,21],这些算法均有效地推动了早期聚类研究的发展。其中,由于基于谱聚类的聚类方法具有不受样本空间形状限制的优点,使得越来越多的研究者开始聚焦于这一领域。

随着近年来数据的爆炸式增长,传统的聚类算法在处理这些大规模数据时已经很难满足人们的需求。例如,谱聚类的计算复杂度为O(n2d+n3)[15](n为样本数,d为特征维数),其中O(n2d)是构造n×n的相似度矩阵所需的计算复杂度,O(n3)是对相似度矩阵进行特征分解所需的计算复杂度。当样本数或者样本特征维度急剧增加时,谱聚类的效率会显著降低。特别是当样本数增加到某一临界值时,由于计算机内存的限制,谱聚类将崩溃。因此,如何有效地对大规模数据聚类已逐渐进入大众的视野,并逐渐占据了重要的地位。

对于大规模的无标签数据,特别是多样本点数据或高特征维度数据,研究人员提出了许多快速的聚类算法。例如,基于矩阵分解的方法中,非负矩阵互分解算法[22](FNMTF)和局部保留非负矩阵互分解算法[22](LPFNMTF)直接将因子矩阵约束为聚类指示矩阵,模型的优化部分为只需少量矩阵乘法的快速更新规则,从而可有效降低处理大规模数据时的计算复杂度。类似地,双边k均值算法[23](BKM)作为一种基于k均值的加速方法,受到FNMTF的启发,并在其基础上将吸收因子约束为对角矩阵,进一步提高了对大规模数据的聚类效率。同时,在过去的一段时间里,各种加速谱聚类算法也被陆续提出,如基于二分图的大规模多视图谱聚类算法[9](LMVSCB)、大规模谱聚类算法[24](LSC)、针对大规模数据的谱聚类算法[25](SCLD)、分布式系统中的并行谱聚类算法[26](PSCD)等,这类算法常常通过优化建图模块(采用不同的映射或采样方法)或特征分解模块来降低计算复杂度。尽管这些尝试都能在一定程度上提高大规模数据的聚类效率,但它们仍存在自身的缺陷。例如,当数据维数变大时,基于矩阵分解方法的效率显著降低,而基于加速谱聚类的方法在处理大规模数据时,由于对特征分解的需求,仍然非常耗时。因此,如何进一步提高大规模数据的聚类效率仍然是一个亟待解决的问题。

另一方面,真实世界数据中存在大量不同分布的噪声和离群点,特别是在高维数据[27-28]中,它们往往对聚类算法的性能有很大影响。如何抑制这些噪声和离群点对聚类性能的影响也是当前的一个热点问题。目前,主流的方法是用L1范数[10]或L2-1范数[29]代替传统的均方误差(MSE),提高聚类的鲁棒性,这在许多应用中已经被证明是有效的。但是,它们仅能有效地抑制线性或高斯分布的噪声,对大量非线性和非高斯分布的噪声及离群点的抑制效果是非常有限的。针对这个问题,GCCF[12](基于相关熵的图正则概念分解算法)将相关熵[30-33]引入到聚类模型中,利用相关熵对非线性和非高斯分布的噪声以及离群点良好的抑制功能,有效地提高了聚类算法的性能,但由于其具有O((n2c+ndc+n2d)t)(c是聚类数,t是迭代次数)的计算复杂度,很难被应用于大规模数据的聚类中。

针对上述问题,本文提出了一种基于相关熵的快速聚类方法(FCC)。在图正则约束的条件下,最小化k均值得到的类别标签与图聚类得到的类别标签之间的误差。由于本文方法兼顾了k均值与图聚类的聚类结果,故此也继承了二者各自的优点,可进一步提高聚类的性能。另一方面,由于本文方法最小化两种聚类算法的聚类指示阵(n×c),与数据矩阵(n×d)或相似度矩阵(n×n)相比,更适合于处理大规模数据,特别是大规模高维度的数据。此外,受GCCF的启发,FCC采用相关熵来度量误差,提高了算法对非线性、非高斯噪声和离群点的抑制能力,从而有效地提高了聚类性能。

本文的主要贡献如下:

(1)提出了一种基于相关熵的快速聚类算法,该算法能有效地对真实世界数据(包含大量非线性和非高斯分布的噪声以及离群点)进行聚类。特别是在面对高维数据时,FCC的效率远远高于现有的快速性方法。

(2)由于引入了相关熵,FCC的目标函数变为难以直接求解的非凸函数。本文提出了一种基于半二次(HQ)极小化技术的优化策略,可以通过较少的迭代次数提高求解效率。此外,本文还分析了FCC的计算复杂度和参数敏感性。

(3)本文在4个不同的真实大规模数据集(包含两个多样本点数据集和两个高特征维度数据集)上进行了大量的实验,结果表明,与目前主流的快速聚类算法相比,FCC能够更快地获得比这些算法更好的聚类性能。

1 相关工作

1.1 相关熵

在信息论学习(ITL)中,为了抑制信号中非线性和非高斯分布的噪声以及离群点引起的不可预测的误差,研究人员提出了相关熵[30]的概念,它可以根据两个随机变量X和Y定义为

V(X,Y)=E[κ(X,Y)]=∑κ(x,y)dFXY(x,y)

(1)

式中:E[·]表示期望算子;κ(x,y)是移位不变Mercer核;FXY(x,y)表示(X,Y)的联合分布函数。本文采用的核函数为

κ(x,y)=G(x-y)=exp(-(x-y)2/2δ2)

(2)

式中:δ>0表示高斯核的核带宽参数。在实际中,由于能获得的样本数量有限,联合分布函数往往是未知的。因此,相关熵通常表示为以下形式

(3)

1.2 半二次技术

半二次(HQ)技术[27,32-33]由于能够求解ITL中的非线性和非凸损失函数,在图像处理、模式识别和鲁棒估计中得到了广泛的应用。对于随机向量x∈Rn,x的潜在损失函数f(x)可定义如下

(4)

式中:xi表示x的第i个元素。引入xi的辅助向量z,可以将式(4)的增强函数定义为

(5)

式中:zi仅依赖于f(xi);g(zi)是f(xi)的双势函数;Z(xi,zi)表示HQ函数。本文利用了广泛使用的HQ函数的乘法形式,表示如下

(6)

式中:z=[z1,…,zn]是辅助量。结合式(5)和式(6),势函数的向量形式如下

(7)

2 FCC模型

本文提出的算法能够有效地处理包含噪声(特别是非线性和非高斯分布的噪声)以及离群点的大规模数据。FCC主要由两步组成:利用k均值生成粗聚类标签,并将其作为真值输入到第二步;利用第一步输入的标签矩阵,在图正则约束的条件下完成基于锚点图的聚类。因此,FCC不仅继承了k均值和图聚类的优点,而且大大降低了计算复杂度。此外,引入相关熵可以有效地抑制真实数据中的噪声和离群点对性能的影响,从而有效提高聚类算法的性能。

假设X=[x1,x2,…,xn]T∈Rn×d是一组包含c类的无标签大规模数据。在FCC的第一步中,需要使用k均值为每个样本生成粗类别。更准确地说,这一步需要生成一个指示矩阵C∈Rn×c,它的每一行只有一个元素1,其余元素都是0。因此,在后续的图聚类过程中,FCC还可以继承k均值得到的原始数据的内部结构。此外,得到的指示矩阵C代替原始数据矩阵X作为第二步聚类的输入,可以大大降低需要处理的数据规模,从而提高对大规模数据聚类的效率。

FCC的第二步需要在原始数据和它们的锚点之间构造一个锚点图[34],然后利用锚点图的拉普拉斯矩阵作为正则约束来完成图聚类过程。该步骤继承了图聚类不受样本空间形状的限制以及具有良好的数学框架的优点。同时,锚点图的构造大大降低了数据的维度,保证了处理大规模数据时的高效性。

在构造锚点图之前,首先需要生成锚点。目前,主流的锚点生成方法主要有随机采样法和k均值两种。实践证明,使用随机采样和k均值生成相同数量的锚点,由k均值生成的锚点往往能在后续聚类过程中获得更高的聚类性能,因此本文采用k均值生成锚点。

设U=[u1,u2,…,um]T∈Rn×d为用k均值生成的X的锚点,锚点图矩阵可用下式表示

(8)

式中:H为原始数据与其锚点之间的锚点图矩阵;xi和uj分别为X和U中的第i行和第j行;Δi表示{1,2,…,m}的一个子集,{1,2,…,m}为U中xi的k近邻的个数;ψ(a,b)可以表示为

(9)

其中σ是一个名为高斯核带宽(GKB)的自由参数,它决定着式(9)的鲁棒性。

此时,数据X与其锚点之间的锚点图矩阵对应的相似度矩阵W可表示为

W=HHT

(10)

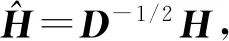
(11)

(12)

因此,与L的p个最小特征向量相对应的W的p个最大特征向量Σp可以按如下公式计算

(13)

式中:Λp是Λ的前p列;Πp是集合(ε1,ε2,…,εp)对应的对角矩阵。

结合第一步得到的粗标签C和本部分基于图约束的聚类方法,可以定义如下聚类公式

(14)

式中:Zp=Rp×c是辅助变量矩阵。

此外,为了处理大量的各种分布的噪声,特别是各种非线性和非高斯的噪声以及实际数据中的离群点,在式(14)中引入相关熵,即可得到FCC的目标函数如下

(15)

当式(15)达到最大值时,ΣpZp和C之间的误差最小。此时,可以直接从ΣpZp获得最终的数据类别。

3 优化与分析

为了求解FCC的目标函数,本节提出了一种新的交互式迭代求解策略。在优化之前,首先需要利用半二次最小化技术将式(15)转化为凸函数如下

(16)

式中:ei是HQ技术的辅助量。由于式(16)是一个凸函数,故可直接优化求解。具体来说,式(16)需要在固定Zp的条件下最大。此时,ei可通过以下公式获得

(17)

式中:σ是影响相关熵鲁棒性的自由参数,表示为

(18)

此时,式(16)可以表示为如下形式

(19)

等价于以下优化问题

(20)

式中:ri=-ei/σ2。在此基础上,式(15)的优化问题转化为只需交互迭代求解R=diag(r1,r2,…,rn)T和Zp,使式(20)最小化。

更新R:R是对角矩阵,对角线元素为Rii=ri,其中ri可表示为

(21)

更新Zp:为了求解Zp,式(20)可以重新写成如下矩阵形式,其中Y=ΣpZp

(22)

根据矩阵迹的性质,如tr(AB)=tr(BA)和tr(AT)=tr(A),式(22)可变换为以下形式

λtr(YTLY)

(23)

对应的拉格朗日函数可定义为

L=tr(YTRY)-2tr)CTRY)+tr(CTRC)+

λtr(YTLY)+tr(φYT)

(24)

式中:Φ=[Φ]ij∈Rn×c是拉格朗日乘数。然后,可以导出拉格朗日函数的偏导数

(25)

转换如下

2(RY)ijYij-2(RTC)ijYij+2λ(LY)ijYij+

ΦijYij=0

(26)

利用KKT条件(如ΦijYij=0),式(26)可转化为

2(RY)ijYij-2(RTC)ijYij+2λ(LY)ijyij=0

(27)

因此,可得到如下更新规则

(28)

由于Y=ΣpZp,Zp可通过下式计算

(29)

此外,Zp可按照以下规则进行归一化

(30)

利用以上更新规则迭代更新R和Zp,直到目标函数收敛,完成聚类的全过程。此时,样本的类别可以直接从Y中得到。详细的FCC算法如下。

算法:基于相关熵的快速聚类算法(FCC)

输入:原始数据X、锚点数量m、前p个引导特征向量、类的数量c和参数λ。

输出:所有样本的聚类类别Y。

1:使用k均值生成m个锚点。

2:利用式(8)构造锚点图。

3:计算度矩阵D和拉普拉斯矩阵L。

4:设Zp∈Rp×c为随机正矩阵,σ由式(18)得到。

5:while不收敛do

6:通过解式(21)更新R。

7:通过解式(28)、式(29)和式(30)更新Zp。

8:end while

9:由Y直接获取样本类别。

FCC的计算复杂度主要由生成锚点、构造锚点图和迭代优化几个部分组成。这些部分的复杂性分别如下。

(1)利用k均值从n个样本中生成m个锚点,需要O(nmdt1)的复杂度,其中d是样本的特征维数,t1是k均值的迭代次数。

(2)利用式(8)在n个样本和m个锚点之间构建锚点图时,需要O(nmd)的复杂度。

(3)优化时需要的复杂度为O((nc2+npc)t2)。准确地说,求解R需要O(nc2)的复杂度,更新Zp需要O(npc)的复杂度,t2是目标函数收敛时的迭代次数。

因此,FCC的总体计算复杂度为O(nmd(t1+1)+(nc2+npc)t2)。由于在处理大规模数据时m、d、p、c、t1和t2比n小得多,因此FCC的复杂度可以近似为O(n)。特别是当数据的维数较高时,FCC在求解目标函数时与数据维数无关,因而仍能保持较低的计算复杂度。

4 实 验

4.1 数据集

本文使用WebKB[35]、TDT2[12]、Mnist[36]和Cora[37]4个常用的真实数据集测试了FCC和其他典型算法的聚类性能。其中,WebKB是一种广泛应用于聚类算法的真实文本数据集,本文采用随机采样得到827个样本点共7类数据,组成新的WebKB数据集来测试所有算法的性能;TDT2包含了11 201个主题文档,本文删去了少于30个文档的那些类别,组成了新的包含9 394个文档共30类的新的TDT2数据集;Mnist是一个包含60 000个训练样本和10 000个测试样本的手写体数字数据集,本文在训练集中针对每一类随机采样,组成了具有6 996个样本共10类的新的Mnist数据集;Cora数据集为计算机科学领域的研究论文集,类似地,我们利用随机采样得到了包含7 511个样本共10类的新的Cora数据集作为本文中所使用的算法的测试数据。各数据集具体情况见表1。

表1 数据集描述Table 1 Description of all datasets

4.2 对比方法

为了验证FCC的性能,本文选取了几种典型的快速以及鲁棒的聚类算法FNMTF、BKM、LPNMTF、LSSC和KMM作为对比,对比算法的详细情况总结如下。

FNMTF[22]:一种基于矩阵分解的快速聚类算法,它将因子矩阵直接约束为聚类指示矩阵,并提出了一种只包含少量矩阵乘法的优化算法。

BKM[23]:一种快速的双边k均值算法,在约束因子矩阵为聚类指示矩阵的基础上,进一步将吸收因子矩阵限制为对角矩阵。

LPFNMTF[22]:一种新的局部保留正则化的FNMTF方法,该方法通过增加流形正则化来实现对两个分解因子矩阵的几何约束。

LSSC[10]:一种稀疏的鲁棒大规模聚类算法,由于L1范数的稀疏性和鲁棒性,该模型利用了L1范数约束带有图正则的聚类模型。

KMM[13]:一种最新的高精度扩展k均值方法,它将问题形式化为一个优化问题,这些子问题采用交替优化策略分别求解。

4.3 评估指标

(1)聚类精度[38]:衡量簇与类之间的一一对应关系,可以表示为

(31)

式中:xi为第i个样本的真实标签;yi为相应的习得标签;map(yi)为使用Kuhn-Munkres算法[39]从学习标签到真值标签的转换,f(x,y)取值如下

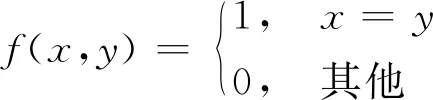
(32)

(2)归一化互信息[40]:通常用于度量聚类结果的相似度,其定义如下

(33)

式中:I(xi,yi)表示互信息;E(·)表示信息熵。归一化互信息也可以表示为

(34)

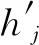
(3)聚类纯度[41]:正确聚类的样本百分比通常用聚类纯度表示,定义为

(35)

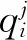
4.4 结果

所有算法均在256 GB的3.50 GHz Intel(R)Xeon(R)CPU E5-1620 v3和Matlab 2019a(64位)平台上运行,聚类结果和计算时间分别如表2和表3所示。其中“—”表示计算时间超过5 h,由于其他算法均能在几千秒甚至几十秒内完成聚类全过程,故此计算时间超过5 h后我们不再关注该算法的性能。结合表2和表3可以看到,与这些算法相比,FCC不仅可以获得更好的聚类性能,而且可以保持最短的计算时间。特别地,由于这些数据集都是真实世界的数据,因此包含了大量不同分布的噪声和离群点。FCC通过引入相关熵可以有效地抑制非线性和非高斯分布的噪声以及离群点对聚类性能的影响,从而可以更快地处理包含大量噪声和离群点的大规模真实世界数据。

表2 所有方法在不同数据集上的聚类结果Table 2 Clustering results comparison of all methods on different datasets

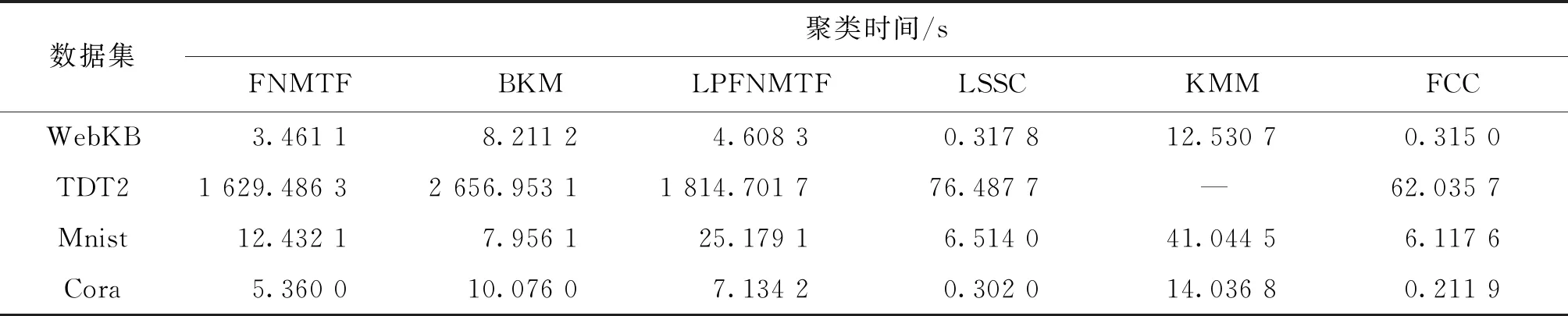
表3 所有方法在不同数据集上的聚类时间Table 3 Computational time comparison of all methods on different datasets

4.5 参数分析

两个参数主要影响FCC的性能和效率,分别是锚点数m和正则项系数λ。本文选取锚点集合为[c+1,c+3,c+5,c+7,c+9,50],图1给出了FCC在不同锚点数的WebKB和Cora上运行的实验结果。可以看出,当锚点数较少时, 随着锚点数的增加,聚类性能逐渐提高。当锚点数增加到一定程度时,聚类性能相对稳定,不再大幅度增加。同时,随着锚点数量的不断增加,计算时间也在不断增加。因此,选择合适数量的锚对聚类性能和效率有很大的影响。

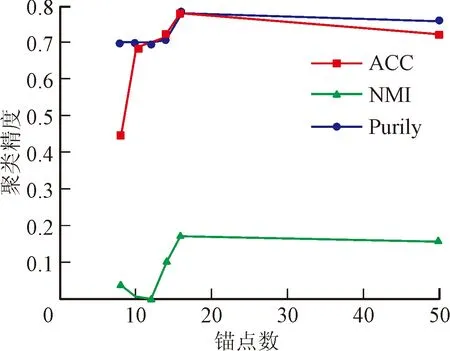
(a)不同锚点数在WebKB上对应的聚类结果

图2展示了具有不同λ的FCC的聚类结果和计算时间,其中λ属于[100,101,102,103,104,105]集合。可以看出,总体来说,当λ变化时,聚类精度和聚类纯度相对稳定,最大互信息波动较大。另外,计算时间随着λ的增加总体保持稳定波动。因此,合适的λ往往会带来较好的聚类性能和短的计算时间。

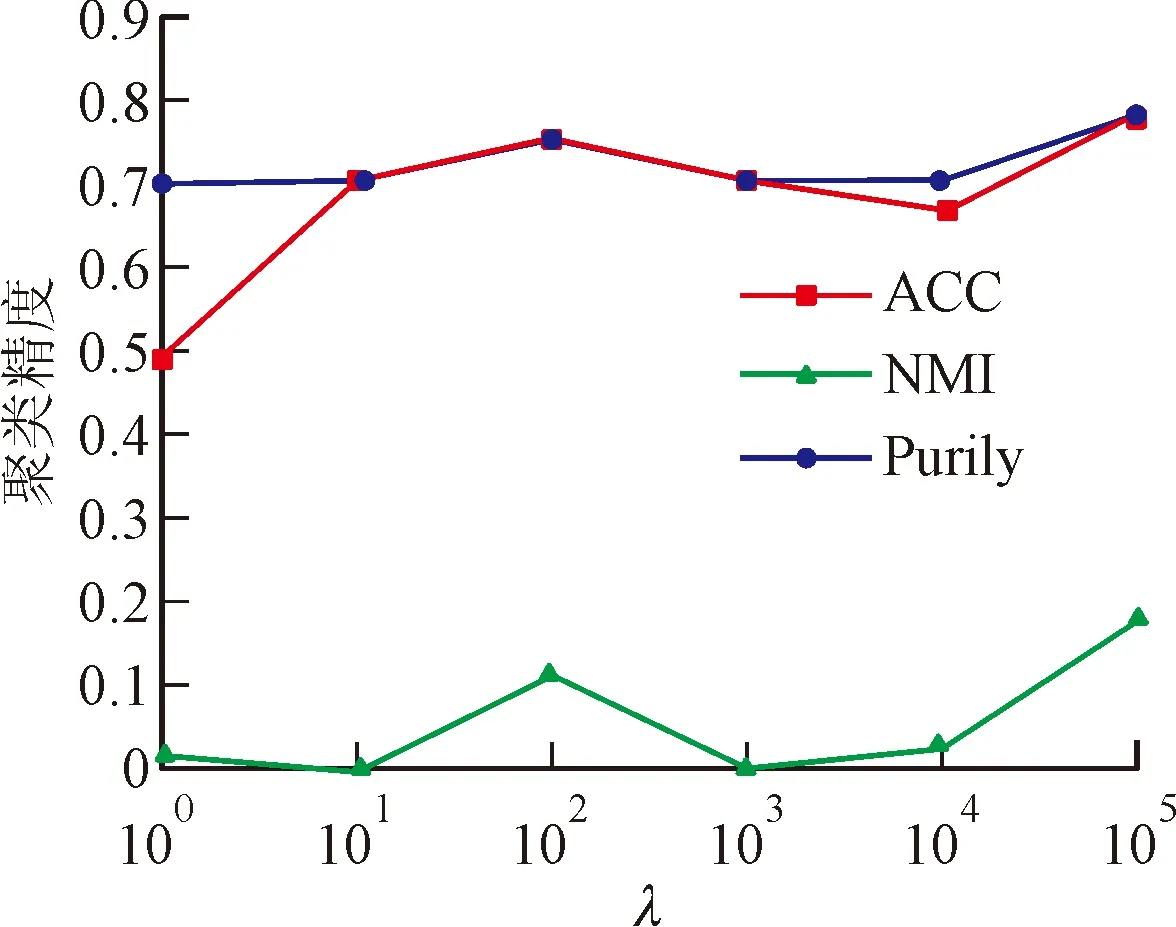
(a)不同λ在WebKB上对应的聚类结果

4.6 鲁棒性分析

为了进一步验证本算法对噪声(特别是非线性和非高斯噪声)的抑制效果,本文以WebKB和Cora数据集为例,对其分别加入10%和20%的随机噪声和泊松噪声,构成含噪数据集作为鲁棒性测试的数据集。图3给出了不同算法在不同噪声条件下的聚类精度对比,从中可以看到,相对于其他对比算法,特别是鲁棒的算法LSSC和KMM,本文方法均可在各种噪声条件下达到优于它们的聚类精度且性能几乎不随噪声程度的增加明显变化,故此本文算法是一种能够高效处理含噪真实数据的鲁棒性算法。

(a)随机噪声腐蚀状态下算法在WebKB上的聚类精度

5 结 论

本文提出了一种基于相关熵的快速聚类算法(FCC),以k均值生成的标签矩阵代替原始数据作为图聚类的输入,以锚点图代替传统图,降低了数据的维数,可以有效处理大规模的真实数据。同时,通过相关熵有效降低了实际数据中的噪声以及离群点对算法性能的影响,极大地提高了聚类算法的性能。在真实世界大规模数据集上的实验表明,相对于那些典型的聚类算法,FCC能够在最短时间内达到良好的聚类性能。