基于楼板组合效应的梁柱子结构抗倒塌性能研究

钟炜辉， 谭 政， 宋晓燕， 孟 宝， 郑玉辉

(1. 西安建筑科技大学 土木工程学院，西安 710055；2. 西安建筑科技大学 结构工程与抗震教育部重点实验室，西安 710055)

建筑结构因撞击、爆炸、地震以及火灾等偶然荷载作用于结构时，会造成结构局部传力构件失效，进而引起其他构件失效或整体结构失稳，甚至导致建筑物大范围倒塌的现象称为连续倒塌。连续倒塌最大的特点就是结构的最终破坏与诱发连续破坏的初始局部破坏不成比例[1]，结构的连续倒塌一旦发生往往会造成很严重的生命财产损失。钢框架中的竖向承重构件(柱)发生破坏后，可首先通过梁机制和压拱机制传递上方框架部分的重力荷载，进入大变形阶段后，悬链线机制依靠梁柱构件的有效拉结以及节点良好的转动能力，逐渐发挥并最终占主导作用。

针对框架结构进行连续倒塌条件下的性能研究常采用备用荷载路径法，即拆除结构的关键柱以模拟连续倒塌工况，国内外学者为此开展了大量研究工作。史艳莉等[2]以圆钢管混凝土柱-H钢梁内隔板式节点双半跨梁柱子结构为研究对象，对影响组合节点抗倒塌承载力的8个关键性参数进行分析，发现增大钢梁强度和减小跨高比可显著的提高节点倒塌抗力。Wang等[3]取双半跨梁单柱型子结构为研究对象，通过静力加载试验研究了节点在中柱失效条件下的破坏模式和抗连续倒塌性能，但是由于双半跨单柱型梁柱子结构模型未考虑子结构在破坏过程中梁反弯点的位置变化，不能很好的反映由于子结构局部破坏导致的后续传力路径变化发展全过程，而采用两跨三柱型子结构可避免此问题；Yang等[4]以腹板双角钢和平齐端板连接组合梁柱子结构(两跨三柱型)为研究对象，通过试验探究了其在倒塌工况下的破坏模式及抗力机制，并且详细阐述了采用双半跨梁柱子结构简化模型取法的不合理性；Ren等[5]以5个单向梁板子结构和2个1/3缩尺无楼板连续梁试件为研究对象，分析了试件在中柱移除情况下的破坏过程和破坏机理，并重点研究了梁高、板厚、板宽等重要参数对结构的抗倒塌能力的影响；笔者对于两跨三柱型纯钢框架梁柱子结构的抗连续倒塌性能也开展了一些研究工作[6-9]，发现跨度比、不同节点刚度以及梁柱连接方向(强轴、弱轴)等参数对于结构的抗连续倒塌性能有着较大影响。截止目前，国内外关于钢框架梁柱子结构抗倒塌机制的研究，主要集中在纯钢框架或钢筋混凝土框架梁柱子结构的研究上，楼板与钢梁形成的组合效应多不考虑。

本文基于备用荷载路径法以组合梁柱子结构为研究对象，对试件进行单调静力加载试验，重点研究在连续倒塌工况下组合梁柱子结构的破坏模式和力学机理。同时采用软件Abaqus建立相关模型，并用试验结果加以验证。基于此模型，分析了周边构件的轴向约束对组合梁柱子结构的抗倒塌承载能力的影响。最后详细分析了组合楼板效应对结构抗倒塌性能的影响，可为该类连接形式的组合框架结构抗倒塌分析和设计提供参考。

1 试验概况

1.1 试件设计

参照GB 50017—2017《钢结构设计标准》[10]和JGJ 138—2016《组合结构设计规范》[11]按1∶3缩尺比例设计了两跨三柱型组合梁柱子结构试件。组合梁跨度取为1 500 mm，由于在子结构选取时，边柱的反弯点近似位于其层高中部位置，上下反弯点的距离为层高，故边柱长度Lc取为1 100 mm，钢梁截面规格为150 mm×100 mm×6 mm×9 mm，钢柱截面规格为150 mm×150 mm×8 mm×10 mm。楼板宽度为600 mm，厚度为55 mm，将混凝土板内纵向钢筋的端头焊接在端板上，钢筋采用HPB300热轧钢筋，纵向受力筋为φ10@125，分布筋采用φ6@125，上排纵向钢筋与分布钢筋形成钢筋网，经计算其配筋率为0.95%，满足设计要求。组合楼板与钢梁通过直径为13 mm，长为45 mm的抗剪栓钉连接，栓钉采用双排布置，各个栓钉之间的间距为125 mm，满足完全抗剪连接要求。试件采用YX28-200-600型(开口型)压型钢板，厚度为0.6 mm。梁柱节点为FEMA规范[12]推荐的盖板加强型(cover plate strengthen,CPS)栓焊连接节点，梁腹板与剪切板采用10.9级M16摩擦型高强螺栓连接。试件整体尺寸、节点细部构造及板中配筋间距，如图1所示。

1.2 材性试验

试件各部位钢材(钢梁、钢柱、剪切板、盖板、钢筋、螺栓、压型钢板)均制作3个标准拉伸试件，材性结果平均值如表1所示。混凝土楼板采用强度等级为C20的混凝土，在浇筑混凝土楼板时制作了边长为150 mm的立方体试块，测得混凝土立方体抗压强度平均值为17.9 MPa，150 mm×150 mm×300 mm棱柱体试块测得混凝土弹性模量平均值为2.41×104MPa。

图1 试件几何尺寸(mm)Fig.1 Details and layout of the specimen(mm)

1.3 加载装置与加载制度

试验设计了一套自平衡加载装置，如图2所示。通过在两边柱底部设置连接件与地梁相连以实现铰接约束条件，为观测中柱失效后结构的内力重分布及其传力过程，将子结构失效柱柱顶加载板与100 t的液压伺服作动器相连，并在失效柱下方设置了竖向滑动约束装置，实现竖向的连续加载。在失效柱处地梁南北两侧方向分别安装了侧向约束装置，以防止试件发生平面外失稳。边柱中部和上部位置通过1 000 kN水平拉压传感器与横梁相连。考虑子结构边柱柱顶仍然受到上部结构传递荷载，通过稳压千斤顶施加轴压比为0.3时对应的荷载模拟上部结构对子结构柱顶的荷载作用。试验每级加载按5 mm施加，加载速率不超过5 mm/min，每级加载完成后持荷3～5 min，直至试件发生破坏。

1.门架; 2.作动器; 3.水平梁; 4.千斤顶梁; 5.横梁; 6.拉压传感器; 7.千斤顶; 8.竖向和侧向约束装置; 9.地梁; 10.铰接连接件。图2 试验加载装置Fig.2 Test setup

1.4 测量方案

试验测量内容主要包括试件位移、梁柱构件关键截面的应变、混凝土板、压型钢板及钢筋应变、梁柱节点转角、边柱中部和上部水平荷载、柱顶荷载等。

图3 测点布置Fig.3 Arrangement of measuring point

其中试件位移的测量包括组合梁竖向变形和边柱中部位置的侧移，以获取组合梁柱子结构的竖向变形特征和周边构件提供的轴向刚度。在梁柱构件上选取8处关键截面布置应变片。其中B1(B6)、B3(B4)截面的应变片主要用于获得梁柱节点区域的受力特征；B2(B5)、C1(C2)截面应变片主要用于获得梁柱构件截面的实际内力，为分析结构的力学机理提供依据；在梁端共布置6个倾角仪I1～I6，用于测量梁端转角；在边柱上端和中部的铰接支座处分别设置了4个1 000 kN水平拉压传感器，用于获取边柱铰支座的水平反力；在边柱顶部设置2个1 000 kN的压力传感器，以监测额定竖向荷载作用。

2 试验结果及分析

2.1 试验曲线与破坏过程

试件在试验加载初期，处于弹性工作阶段，无明显现象。当加载位移达到20 mm时，两跨的混凝土板边柱翼缘位置同时出现首条受拉裂缝，随着位移增加至35 mm时，两跨跨中开始相继出现斜向裂缝(纵向对称)，板中部出现一条纵向受拉裂缝。混凝土板裂缝随着加载位移的增加不断发展并加宽。当加载位移达到95 mm时，西侧钢梁下翼缘(靠近节点J2)发生屈曲，压型钢板开始撕裂。同时在东侧钢梁上翼缘(靠近节点J3)发生屈曲，压型钢板出现鼓起，与边柱Z1相连的西侧钢梁下翼缘出现了受压局部屈曲，由于试件的对称性，东侧组合梁试验现象与西侧组合梁的试验现象基本一致，如图5(a)、图5(b)所示。当位移增加至120 mm时，失效柱板顶混凝土开始脱落。当位移增加至195 mm时，失效柱梁柱节点处西侧钢梁紧靠盖板末端的受拉翼缘出现裂缝，当位移发展至201 mm时，随着一声脆响，钢梁受拉翼缘发生断裂，如图5(c)所示，对应荷载为327 kN(图4曲线关键点F1)。随着失效位移的不断增大，西侧钢梁下翼缘裂缝逐步沿着弧线向上发展，在此期间可以明显听到钢筋断裂的声响。由于左右两跨组合梁之间的协同作用可使得结构的荷载逐步回升并超过第一峰值荷载达到396 kN，裂缝贯穿腹板上部螺栓孔并最终导致钢梁腹板断裂，此时对应加载位移为333 mm(图4曲线关键点F2)，如图5(d)所示，试件破坏加载终止。可以看到，失效柱处混凝土被压溃，边柱处混凝土严重开裂，压型钢板被撕裂，如图5(e)、图5(f)所示。混凝土板的最终裂缝分布如图5(g)、图5(h)所示，可以看到，边柱节点附近形成了多条宽度较大的主裂缝，跨中形成多条对称的斜向受拉裂缝，混凝土板中部还形成了有一条纵向贯穿裂缝。可见在竖向荷载作用下，边柱节点受到负弯矩作用，导致混凝土板板顶受拉开裂，且裂缝宽度随着失效位移不断加宽，钢梁下翼缘受压，导致发生受压屈曲；而失效柱节点处受到正弯矩作用，上部混凝土板受压，导致板顶混凝土被压溃。

图4 荷载-位移曲线Fig.4 Load-displacement curve

2.2 边柱水平荷载分析

试件边柱顶部、中部及底部的水平荷载,如图6所示。试验加载前期主要由边柱上下端提供的约束反力组成弯矩来形成梁机制，表现为边柱底部和上部的水平反力为异号。当失效柱达到一定的竖向位移时，边柱中部拉压传感器开始有拉力产生，此时组合梁柱子结构由抗弯梁机制开始向悬链线机制转换，随着变形的不断增大，组合梁的内力将由弯矩为主转变成以弯矩和轴力为主，进入过渡阶段，悬链线机制逐步形成。随着变形的增大，悬链线机制的作用将越来越显著，组合梁呈现二力杆受拉状态。

图5 破坏现象Fig.5 Failure phenomena

图6 边柱水平荷载分布Fig.6 Horizontal reaction distribution of the side columns

2.3 组合梁柱子结构抗力分析

两跨三柱组合梁柱子结构简化模型对应的受力模型,如图7所示。可以看出，梁抗力机制PF由双跨梁截面剪力(V2,V3)的竖向分量之和组成，悬链线机制提供的抗力PC则由双跨梁的轴力(N2,N3)的竖向分量之和组成。根据受力模型，可按照下列公式计算两种抗力机制的抗力水平。

NW=N1=N2，NE=N3=N4

(1)

PC=PW+PE=NWsinθW+NEsinθE

(2)

PF=PV-PC

(3)

式中：NW，NE分别为西侧和东侧组合梁轴力；θ1～θ4分别为西、东侧组合梁的梁端转角。

图7 组合梁柱子结构分析模型Fig.7 Analysis diagram of composite beam-column assembly

基于上述计算模型，图8给出了梁机制及悬链线机制提供的抗力随失效柱竖向位移的发展曲线。可以看出:①在试件加载初期，试件总抗力P几乎完全由梁抗弯机制PF提供，随着加载位移的增大，悬链线机制提供的抗力开始显现；②当试件首次出现局部断裂时，梁端有效截面突然减小，导致抗弯机制提供的抗力迅速下降，而悬链线机制提供的抗力PC此时迅速增大，此过程为梁机制向悬链线机制迅速转变；③随着加载位移至283 mm，悬链线机制提供的抗力PC超过梁抗弯机制的抗力PF并对结构抵抗荷载起到主要作用。

图8 抗力机制发展Fig.8 Development of the resistant mechanism

3 有限元分析

3.1 有限元分析模型的建立

采用Abaqus/Explicit动力显示积分算法对组合梁柱子结构进行非线性有限元分析，根据试验相同的边界条件和试件几何尺寸建立了对应的数值模型，如图9所示。试件主要部件包括钢梁、钢柱、混凝土板、钢筋、螺栓、压型钢板、节点剪切板以及盖板等，采用三维桁架单元T3D2模拟楼板中的钢筋，壳单元对压型钢板进行模拟，对于其余部件均采用C3D8R实体单元进行建模，并在节点应力集中区域划分较密的网格单元。钢材本构曲线采用多点折线模型本构；钢筋采用双折线强化本构；混凝土采用GB 50010—2010《混凝土结构设计规范》[13]附录C给出的受压和受拉应力-应变关系。为模拟试件的断裂过程，采用Abaqus中的延性金属失效准则和单元删除法模拟钢材的断裂，该准则是通过在材料属性中定义材料的断裂应变、三轴应力、应变率等参数，使金属材料达到断裂应变值[14-15]后发生断裂，如式(4)所示

(4)

式中：C1为钢材平板纯剪切下的等效塑性损伤应变；C2为钢材开口圆棒单轴拉伸时的等效塑性损伤应变，可根据轴对称拉伸试件断裂后的截面缩小面积确定

C2=-ln(1-AR)

(5)

同时C1和C2可通过式(6)、式(7)进行换算

(6)

σ=K(ε)n

(7)

式中,K,n为钢材的硬化参数，可由钢材的真实应力-应变曲线反算得出。

图9 有限元分析模型Fig.9 Finite element analysis model

3.2 有限元分析结果

试件数值模型分析结果与试验结果曲线对比,如图10所示。可以看出，由于数值模型未考虑试件材料的各种缺陷，两者存在一定的差异。但整体来说，数值模型得到的荷载-位移曲线与试验结果十分接近，说明动力显示积分算法可以比较准确的模拟试件断裂位置及断裂后发展路径。通过图11可以看出，模型的破坏模式与其对应的试验破坏模式基本一致，证明数值模拟结果具有足够的精度，可以较好的反映组合梁梁柱子结构在大变形下的主要受力特征，满足工程计算要求。

图10 有限元与试验荷载-位移曲线对比Fig.10 Comparison of load-displacement curves between finite element and tests

图11 有限元模拟的试件破坏过程Fig.11 Failure process of the specimen in the finite element simulation

3.3 周边构件提供的轴向约束的影响

实际上，梁端轴向约束对于组合梁柱子结构中悬链线的发展具有较大的影响，组合梁梁端轴向约束刚度由以下三部分组成：①组合梁自身变形对梁端提供的约束刚度Kac；②边柱对梁端提供的轴向约束刚度Kas；③周边构件对梁端提供的轴向约束刚度KR。为了研究周边构件提供的轴向约束对组合梁柱子结构承载力的影响，引入弹簧约束系数n，表示周边构件约束弹簧轴向刚度KR与构件本身对梁端提供的轴向弹簧刚度K的比值，并分别取0(外伸梁处完全无约束作用)，0.025(近似门架给试件提供的实际轴向约束)，0.1，1.0，∞。

(8)

系数k为梁柱线刚度比，可按式(9)计算

(9)

式中，各参数表达式可详见GB 50017—2017《钢结构设计标准》。

图12给出了数值模型周边构件提供的不同轴向约束对于栓焊连接试件抗倒塌承载力的影响对比。可以看到，在组合梁柱线刚度比k=0.88为情形下，随着轴向约束刚度KR的增大，组合梁柱子结构的荷载-位移曲线在加载初期基本没有影响，但是随着位移的不断增大，第一峰值点对应的荷载不断增大。结果表明:当n=0时，构件本身对梁端提供的轴向弹簧刚度K不足以充分发挥悬链线效应，无法提高结构的后期承载力；当n=0.025时，试件后期承载力明显有较大的提升，说明此时试件的悬链线效应得到了有效发挥；当n>0.1时，数值模型的承载力基本不再继续增加，说明此时周边构件提供的轴向刚度已足够保证悬链线机制的完全发挥，继续增加轴向刚度对于结构的承载能力的提高作用有限。即周边约束若能提供大于0.1K的轴向刚度时，则可保证组合梁柱子结构的悬链线效应完全发挥。

图12 周边构件轴向约束对试件抗倒塌承载力影响Fig.12 The influence of the peripheral components′ constraints on anti-collapse performance of specimens

4 楼板组合作用

4.1 模型的建立

选取尺寸为4 500 mm×7 500 mm×3 300 mm的原型结构设计了子结构(带楼板和不带楼板)的足尺模型，梁柱截面尺寸分别为450 mm×300 mm×11 mm×18 mm、400 mm×400 mm×13 mm×21 mm。钢梁通过剪切板与柱腹板通过10.9级M22的高强螺栓连接，其中剪切板为L110 mm×12 mm，节点的细部构造如图13所示。混凝土强度等级为C25，有效宽度为1 500 mm，楼板厚度为100 mm，保护层厚度为20 mm，楼板的有效宽度为1 500 mm，纵向钢筋为φ14@150，分布钢筋设计为φ8@200，受力钢筋与分布钢筋形成钢筋网，楼板内设置两层钢筋，具体布置如图13所示。钢梁和组合楼板之间选用φ19的栓钉连接，并设置为双排，间距为210 mm，排距为150 mm。组合梁柱子结构模型与本文试验模型一致，同样为两跨三柱型梁柱子结构，并假定周边构件对组合梁子结构有足够的拉结作用。

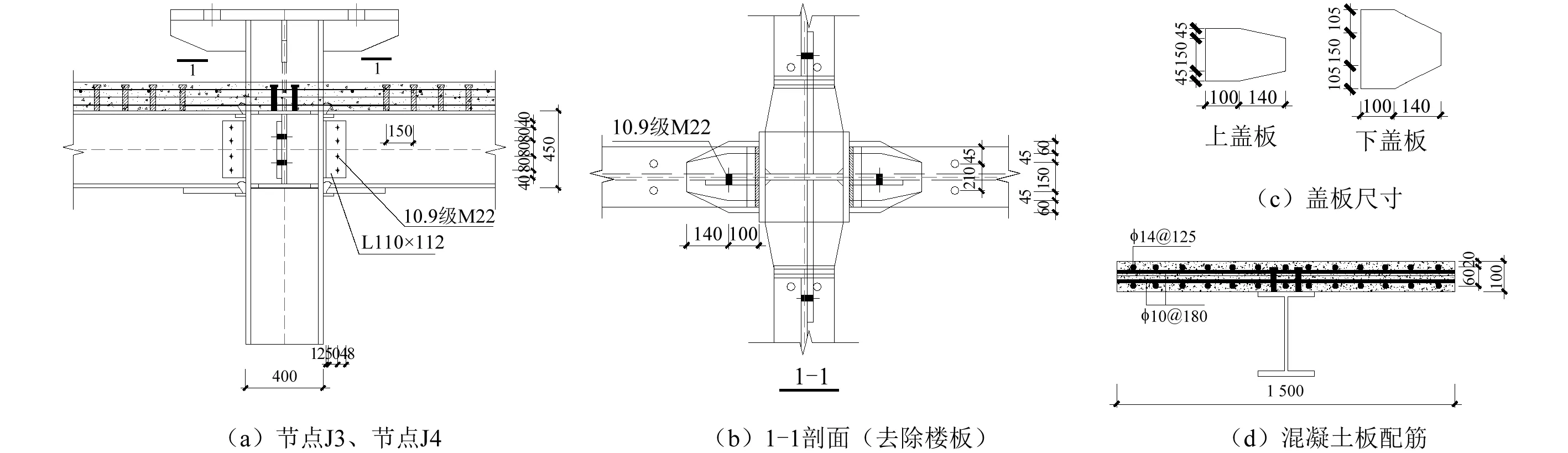
图13 梁柱节点细部构造以及楼板配筋(mm)Fig.13 Details of connections and distribution of reinforcement(mm)

4.2 荷载-位移曲线对比

考虑楼板作用与否对子结构的荷载-位移曲线的影响对比，如图14所示，两个试件模型均存在两次主要断裂破坏点，对应破坏模式类似。首次断裂对应破坏模式为靠近失效柱钢梁下翼缘紧靠盖板末端处母材断裂，纯钢梁柱子结构(WUFG)此时荷载为1 170 kN，对应位移447 mm，组合梁柱子结构(WUFG-CS)荷载为1 656 kN，对应位移478 mm，带楼板模型的首次断裂荷载较无楼板模型提高了41.5%。二次断裂对应破坏模式为靠近边柱的钢梁上翼缘紧靠盖板末端处母材断裂，纯钢梁柱子结构荷载为1 118 kN，对应位移1 137 mm，组合梁柱子结构的荷载为1 519 kN，对应位移1 220 mm，带楼板模型的二次断裂荷载较无楼板模型提高了35.9%。可见，楼板与钢梁之间的组合作用可以有效的提高结构的初始刚度和整个过程的承载能力。

表2 试件荷载-位移曲线断裂点Tab.2 Fracture point of load-displacement curves

4.3 内力发展曲线对比

图15给出了组合梁柱子结构和纯钢梁柱子结构的内力发展过程对比。对比可知：①两者的失效模式均为靠近失效柱处钢梁受拉下翼缘首先发生断裂，进而靠近边柱受拉上翼缘断裂。两者的内力发展趋势也基本一致当达到首次断裂位置时，B3/B4弯矩迅速下降并逐渐转变为负值，对应轴力也发生下降但影响不大，此时截面的中性轴相对原始截面形心轴位置向上翼缘移动，产生偏心弯矩。随着位移的进一步增大，靠近边柱受拉上翼缘断裂，B1/B6弯矩迅速下降并逐渐转变为正值。②楼板的存在可以较为明显的提升结构的压拱效应，进而提高结构的塑性承载能力。楼板内钢筋在小变形阶段由于压拱效应其轴力为负值，试件首次发生断裂时钢筋轴力达到830 kN，占总轴力38%。当发生第二次断裂时，钢筋轴力为860 kN，占总轴力30%。可见，钢筋对试件轴力的发展起到重要作用。③通过截面弯矩对比可以看出，组合梁柱子结构失效柱处B3/B4截面较纯钢梁柱子结构的弯矩更大，且组合梁柱子结构较纯钢梁柱子结构可以推迟结构局部断裂的发生，可为结构位移发展提供有利条件。

图15 内力发展曲线对比Fig.15 Comparison of internal force development

4.4 抗力发展曲线对比

为了定量分析各机制在不同阶段的贡献程度，引入梁机制贡献系数α、悬链线机制贡献系数β，分别按式(10)计算

α=PF/P,β=PC/P

(10)

式中：P为试件的总抗力；PF为梁机制提供抗力；PC为悬链线机制提供抗力。

图16为组合梁柱子结构和纯钢梁柱子结构的抗力发展过程的对比，表3为模型的断裂点对应抗力对比。可知：①两个试件的抗力发展趋势是一致的，均经历梁机制阶段、梁机制和悬链线机制混合阶段以及悬链线阶段，两个试件在首次断裂前，试件总抗力几乎完全由抗弯机制提供，之后有所下降，随后悬链线机制提供抗力迅速增大。当两个试件相继发生第二次断裂后，梁端有效截面面积减小，抗弯机制提供抗力减小为零甚至出现负值，这是因为此时梁截面轴力产生偏心弯矩阻碍结构抵抗外载，最终结构完全由悬链线机制提供抗力。②首次断裂时纯钢梁的抗弯梁机制提供抗力为939 kN，悬链线机制提供抗力231 kN，对于抗弯梁机制贡献系数为0.803，悬链线机制贡献系数为0.197；组合梁柱子结构抗弯梁机制提供抗力1 218 kN，悬链线机制提供抗力438 kN，对应抗弯梁机制贡献系数为0.736，悬链线影响系数为0.264。这是由于组合梁柱子结构较纯钢梁柱子结构的初始抗弯刚度大，导致试件WUFG-CS的梁机制抗力高于试件WUFG，并且钢筋在首次断裂时轴力已较为明显，导致两者的悬链线机制提供抗力也存在一定差距。说明首次断裂时两者承载能力的差值原因主要体现在子结构梁机制和悬链线机制两个方面。③二次断裂时纯钢梁的抗弯梁机制提供抗力为69 kN，悬链线机制提供抗力1 049 kN，对应抗弯梁机制贡献系数为0.062，悬链线机制贡献系数为0.938；组合梁柱子结构抗弯梁机制提供抗力-34 kN，悬链线机制提供抗力1 553 kN，对应抗弯梁机制贡献系数为-0.022，悬链线机制贡献系数为1.022。由于试件WUFG-CS的楼板内钢筋在大变形阶段发挥了重要作用，所以导致大变形阶段两者承载能力的差值原因主要体现在子结构悬链线机制方面。可见楼板与钢梁的组合作用对结构整个过程的承载能力提高起到了关键作用。

表3 断裂点对应抗力对比Tab.3 Comparison of the resistance at fracture points

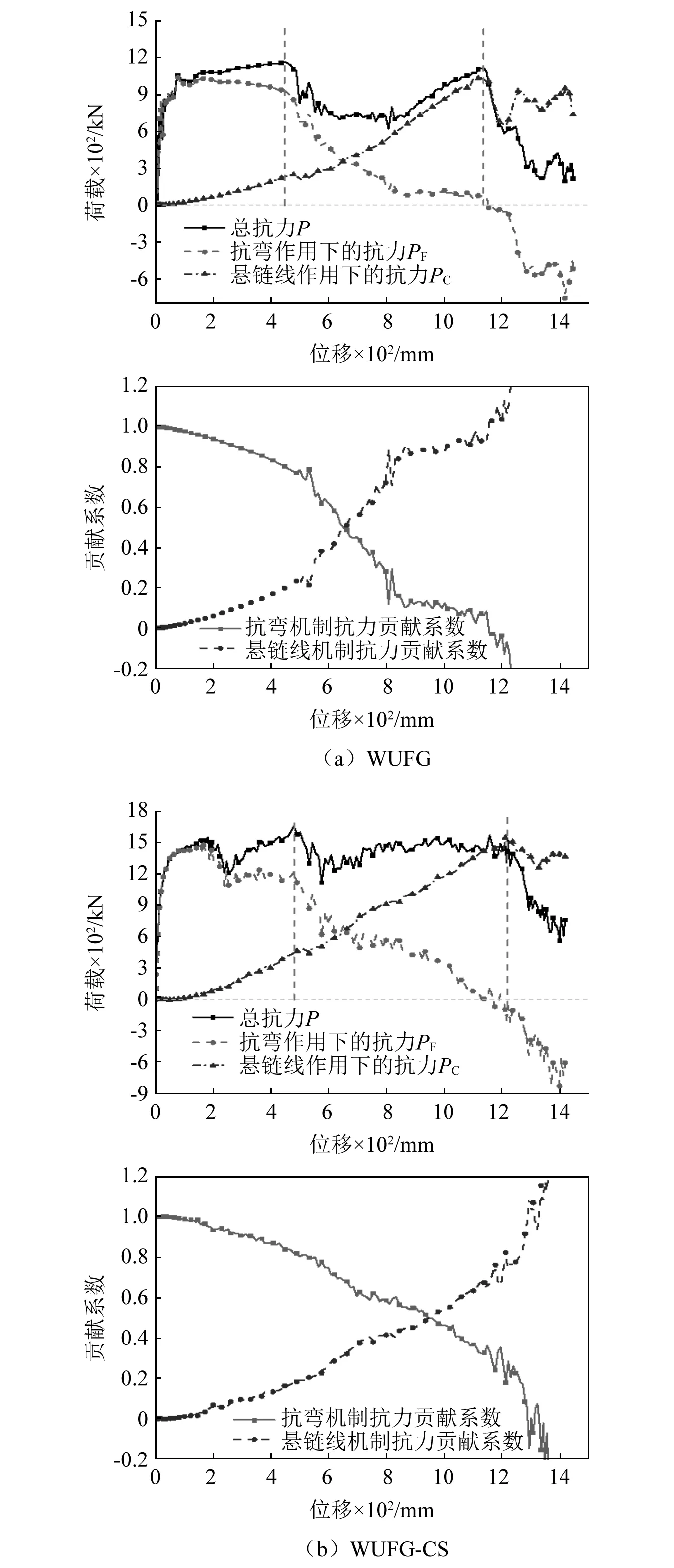
图16 不同机制抗力发展曲线及贡献系数Fig.16 Development curves of the different resistances mechanism and contribution coefficients

4.5 组合梁柱子结构的动力响应

上述试验与有限元模型都是近似静力加载方式进行分析，但是在实际工况中，非偶然因素造成柱失效是瞬间发生的，类似于动力加载过程。为此可根据Izzuddin等[16]不考虑阻尼有利作用的能量评估模型，通过结构静力加载条件下的结果近似得到结构在突加竖向荷载下的动力响应。其原理为动力荷载所做的外力功全部转变为结构的内能，根据图17所示的能量平衡原理可近似得到结构的非线性动力响应曲线。

图17 能量平衡原理Fig.17 Principle of energy balance

图18为2个试件的动力响应曲线。可以看出，纯钢梁柱子结构的动力响应曲线在首次断裂时峰值荷载为1 052 kN，而组合梁柱子结构在发生多次断裂后位移达到1 262 mm对应峰值荷载为1 430 kN，试件WUFG-CS较试件WUFG的峰值荷载提升了36%，位移增大了159%。说明在动力荷载作用下，组合梁柱子结构具有更好的承载能力和变形能力。

图18 动力响应曲线Fig.18 Dynamic response curves

5 结 论

(1)组合梁柱子结构的抗力机制发展过程先后为梁机制阶段、梁机制和悬链线机制混合阶段以及悬链线机制阶段，在中柱失效工况下，结构通过内力重分布，使得剩余结构在大变形阶段仍然具有良好的承载能力。

(2)组合梁柱子结构的破坏模式表现为：失效柱梁柱节点处钢梁紧靠盖板末端的受拉翼缘首先断裂，进而内力转由腹板螺栓传递，裂缝不断向上发展，贯穿上排的螺栓孔直至腹板断裂。当钢梁受拉翼缘发生破坏后，左右两跨组合梁之间的协同作用可使得结构在后期阶段可提供高于前期受弯阶段的抗力，表现出较为富余的后期强度储备。

(3)周边构件的轴向约束对梁柱子结构的后期抗倒塌承载能力有着较大影响。当0≤n≤0.1时，周边构件提供的轴向约束可以提高双跨梁的竖向承载力；当n>0.1时，继续增加轴向刚度对于双跨梁的竖向承载能力影响很小。由此可知，组合梁柱子结构的承载能力并不能随着周边构件轴向约束的增大而无限增大。

(4)考虑楼板组合效应，梁机制峰值承载力提高了42.0%，悬链线机制峰值承载力提高了49.9%。说明楼板组合效应显著的提高了结构在梁机制和悬链线机制的承载能力，并且楼板的存在可使结构在动力荷载作用下具有更好的抗倒塌能力。