冲击载荷下分段线性刚度能量阱的优化研究

崔泰毓， 张 雷， 贾学志， 魏 磊

(1. 中国科学院 长春光学精密机械与物理研究所，长春 130032；2. 中国科学院大学,北京 100049； 3. 长光卫星技术有限公司，长春 130031)

在发射阶段，卫星会经历运载火箭发动机点火，火工品爆炸等一系列冲击激励。对于光学遥感载荷而言，这种过度振动可能会使高度轻量化的光学部件产成不良影响甚至永久破坏。在航天器振动抑制领域，非线性能量阱吸振器以其以其振动能量耗散效率高，鲁棒性好和质量小的特点[1-2]，已越来越多的被应用于航天设备振动抑制中[3-6]。非线性能量阱(nonlinear energy sinks,NES)是一种被动减振设备，它附加在主结构(即振动抑制对象)上，通过能量定向传递现象(target energy transfer,TET)对主结构的振动能量进行高效的吸收和耗散。

能量定向转移是指一定条件下，主结构的振动能量可以向NES高效，单向传递的现象。这是NES实现振动抑制的主要原因，故研究NES触发TET的参数条件一直是该领域的研究重点。Vakakis[1]最早发现带有立方刚度的NES受初始冲击载荷大于某个临界值时，系统中才会发生TET。Gendelman等[7]和Lee等[8]研究了NES和主结构的质量比对系统TET的影响，研究证明NES需要在质量比足够小的情况下才能发生TET。Shiroky等[9]引入了复变平均法，通过系统的慢变方程来研究非线性刚度对NES振动抑制效率的影响，结果说明合理的非线性刚度能提升NES吸振效率。熊怀等[10-11]研究阻尼对NES振动抑制的影响，推导了系统能够实现TET的最小阻尼。

上述研究对象都是具有立方刚度的NES，但在工程应用中，完美的立方刚度难以实现，为了使NES更具有工程应用价值，带有分段线性刚度的NES以其易实现，易调节等特点逐渐被学者们所关注。Lamarque等[12-13]通过半解析半数值的方法研究了分段线性刚度NES，发现系统中两振子能量关系与立方刚度类似，能够实现TET现象。目前，尚未有研究直接针对分段线性刚度NES振动抑制效果进行优化，但参考立方刚度能量阱的研究经验，参数优化会使NES性能有显著提升，故对分段线性刚度NES参数优化研究是有必要的。

本文研究冲击载荷下分段线性刚度能量阱的能量传递特性及参数优化。本文首先通过复变平均法推导了表示系统能量关系的慢变方程；得到了慢不变流形极值点的近似表达式；建立了以NES的能量耗散效率为目标的优化模型；最后搭建了悬臂梁振动实验平台，对上述模型所的参数有有效性进行了实验验证。

1 非线性能量阱系统模型

1.1 耦合非线性能量阱系统的动力学模型

光学载荷上某敏感部件的振动抑制模型可简化为如图1所示的二自由度系统，该系统由一个具有线性刚度的单自由度主结构和分段线性刚度能量阱组成。

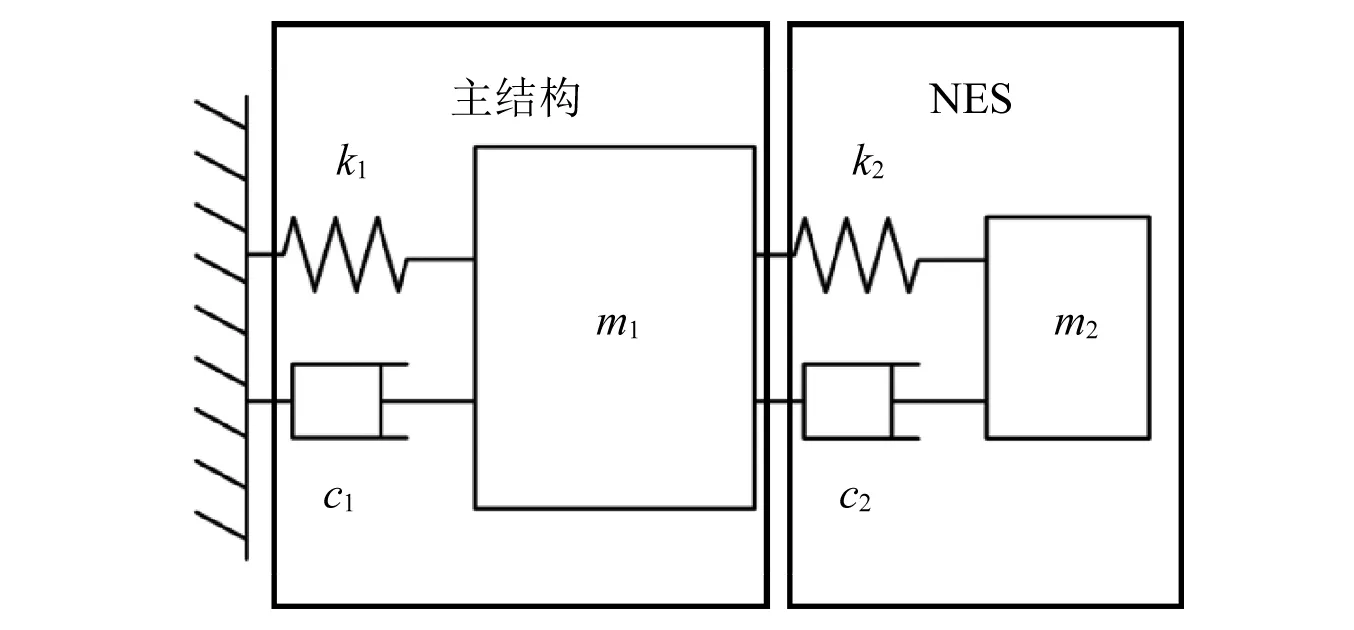
图1 耦合非线性能量阱的系统模型Fig.1 Mechanical model coupled NES

该系统运动微分方程表示为

(1)

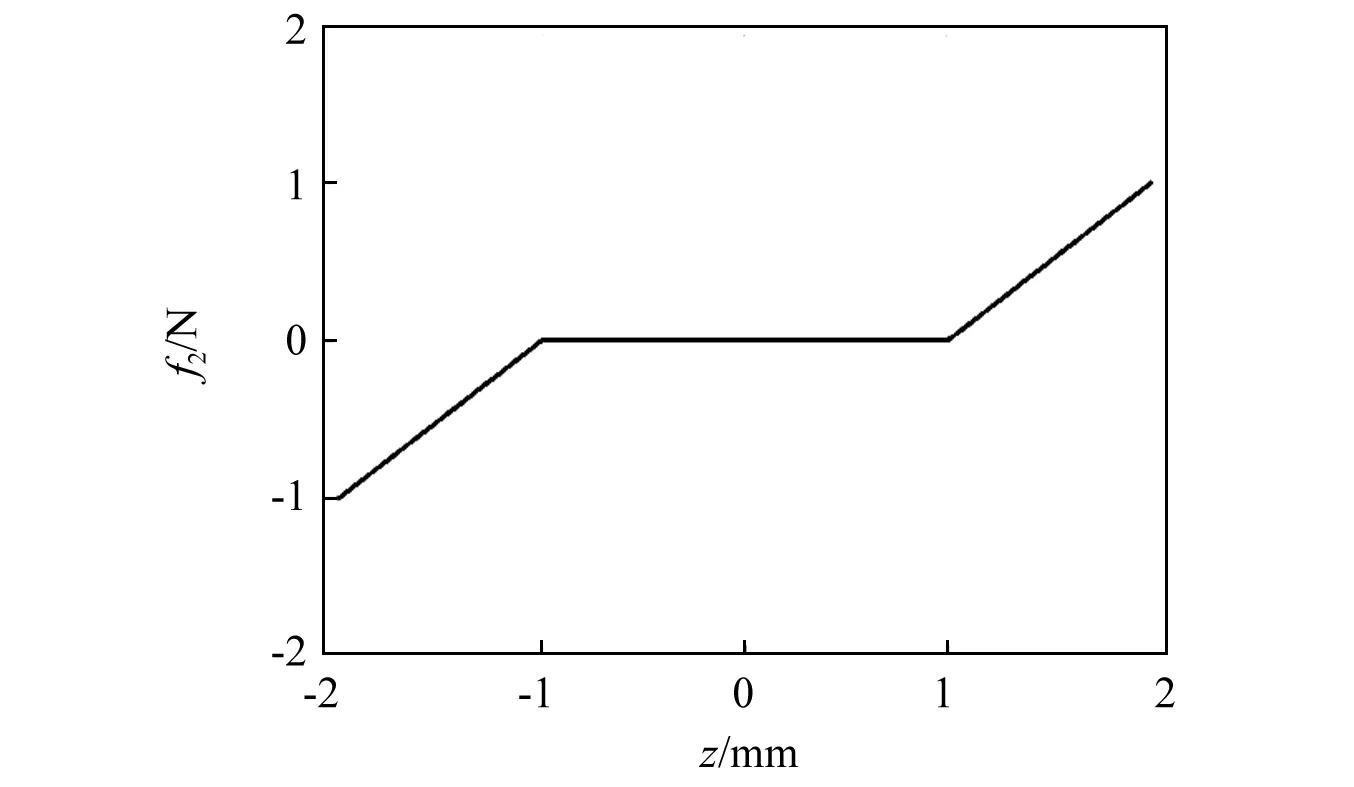
图2 分段线性刚度Fig.2 Piecewise linear stiffness

(2)

式中：z=x1-x2为两振子相对位移；a0为弹簧刚度间隙。

式(1)可简化为

(3)

为计算两振子能量，引入如下变换

(4)

则式(3)化为

(5)

1.2 慢变系统方程

为了分析上述动力学模型中NES触发TET的条件，我们需要分析系统的能量传递特性，但式(5)由于非线性刚度项F2(z)的存在，难以直接求出精确的解析解，这里本文应用复变平均法求解系统能量的近似解析表达式。复变平均法是Gendelman等提出用于求解非线性动力系统的近似计算方法，该方法通过推导原系统的慢变方程得到能量传递关系和能量耗散的近似解。

应用复变平均法首先要引入复变量

(6)

式中:i虚数单位;ω0为系统主结构的固有频率，由于1∶1内共振在能量传递中占据主导地位，本文主要针对1∶1内共振引起的能量传递，故虚部系数为ω0，若要考虑1∶3，1∶5等情况，虚部对应取3ω0，5ω0等。

将式(5)代入式(6)中，并消去久期项得

(7)

(8)

Gendelman[14]曾证明式(8)可化为

(9)

其中，

(10)

将系统的复变量方程式(7)进行如下多尺度展开，取一次近似

(11)

λ1ε(φ10+εφ11)-λ2ε(φ20+εφ21)-

iω0ε(φ20+εφ21)G(|φ21|2)=0

(12)

iεω0(φ10+εφ11)+iεω0(φ20+εφ21)G(|φ21|2)+

ελ2(φ20+εφ21)-iεω0(φ20+εφ21)=0

(13)

系统ε0和ε1系数分别对系统的应快变部分和慢变部分，其中式(12)和式(13)的快变部分为

(14)

iω0φ20=0

(15)

式(12)消去久期项后，慢变部分为

(16)

由复极坐标表示复变量φ10,φ20

(17)

将式(17)代入慢变部分式(16)中，分离实部和虚部后得

(18)

将式(17)代入快变部分式(15)中得

(19)

由上式可得

(20)

其中,

(21)

(22)

式(22)第一式表示慢变系统主结构能量耗散速率，可以看出其仅与两振子能量和阻尼大小有关。

式(22)第二式表示慢变系统中两振子的振动能量传递关系，该式不显含时间，仅与系统结构参数有关，也就是说在冲击载荷下，系统是否能发生TET现象是由主结构与NES结构参数决定的。

2 系统能量传递分析

绘出式(22)的慢不变流形图，如图3所示，图中实线为稳定分支，虚线为不稳定分支，H,L为不稳定点，这与立方刚度非线性能量阱推导得到的形式相同。通过龙格-库塔法得到式(3)数值解如图4所示，当小参数ε足够小时，系统的振动能量会沿着慢不变流形流动。由于存在不稳定分支，系统能量会发生跳跃，也就是产生TET现象。图中参数ε=0.001，ω0=5，k=32，a0=3，λ1=0，λ2=5，下文分析中若无特殊说明均为此参数条件。

不稳定点H,L对应慢不变流形中的两极值点，慢不变流形的不稳定点是否存在对系统是否能够触发TET有重要影响[15]。

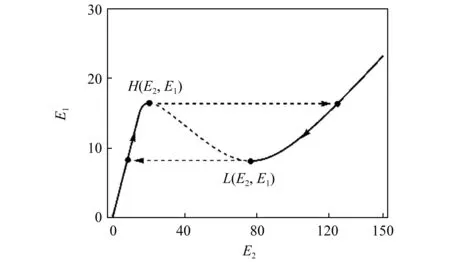
图3 系统慢不变流形Fig.3 Slow invariant manifold of system

图4 慢不变流形与数值解对比Fig.4 Comparison between slow invariant manifold and numerical solutions

2.1 系统触发TET的情况

能够触发TET的慢不变流形如图5所示，在给定的初始条件x1(0)=4情况下，当系统初始能量大于，不稳定点H时，两振子的振动能量会迅速得从初始位置移动到系统慢不变流形的稳定分支2上，并沿着该曲线缓慢移动到不稳定点L，之后振动能量迅速的跳跃到稳定分支1，并沿着该分支缓慢耗散至0。

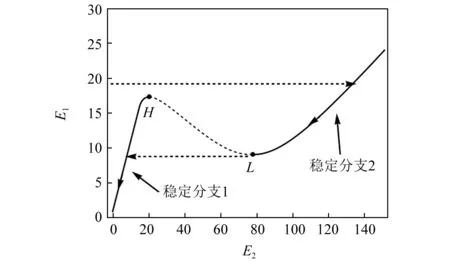
图5 触发TET的慢不变流形Fig.5 Slow invariant manifold of systemthat can trigger TET

2.2 不触发TET的情况

系统不能触发TET分为两种情况：①慢不变流形无不稳定分支；②外激励幅值过小。

当k=24时，慢不变流形无不稳定分支的情况如图6所示。此时，系统无不稳定分支，振动能量会直接移动到稳定流形上，沿着该流形缓慢移动到0，不会发生跳跃，系统不发生TET。

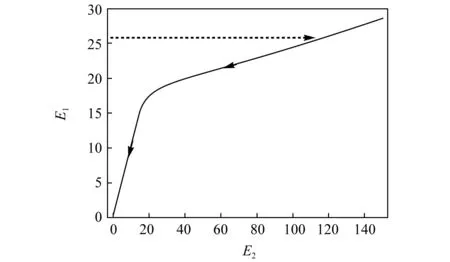
图6 触发TET的慢不变流形Fig.6 Slow invariant manifold of system that can not trigger TET

外激励过小的情况如图7所示，此时系统虽然有不稳定区间，但两振子初始振动能量无法到达稳定流形2，会直接沿着稳定流形1缓慢耗散，不会发生跳跃，此时系统不发生TET。故系统的初始能量需要大于不稳定点L纵坐标E1+，NES才会有吸振效果。

图7 外激励过小无法触发TET的情况Fig.7 The case that the excitation is too small to trigger TET

2.3 不稳定点与能量返还的关系

初始条件x1(0)=4 时，主结构时域响应如图8所示，理想情况下，系统振动能量都应在慢不变流形图的稳定分支2消耗。但我们可以观察到，当不稳定点L的纵坐标E1-不为零时，有部分振动能量从稳定分支1跳跃回稳定分支2，这部分返还的能量无法通过NES的阻尼进行消耗，会对吸振效果产生不利影响。故在设计NES时，应使不稳定点L纵坐标越小越好。

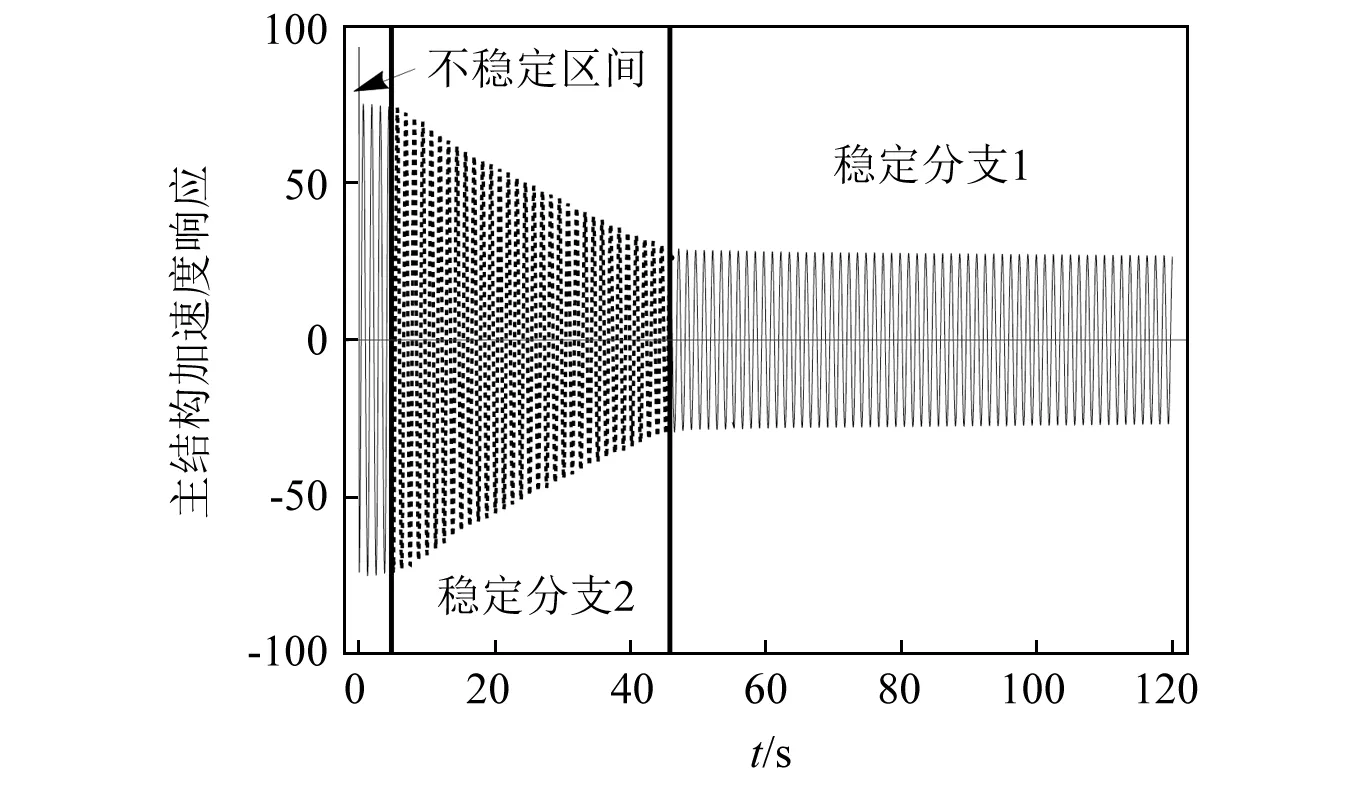
图8 触发TET情况下主结构加速度时域响应Fig.8 Time domain response of acceleration of main structure under the condition of triggering TET

2.4 不稳定点与能量耗散的关系

由图8可知，当系统振动能量处于稳定分支2时的主结构的能量耗散速率最高，远远大于稳定分支1和稳定分支2的能量耗散速度。根据式(22)第一式可知，在主结构阻尼较小的情况下，系统能量耗散速率主要取决于NES的阻尼和E2的大小。增大不定点L的横坐标E2+会使系统在稳定分支2和不稳定区间的能量耗散效率随之增大。不同E2所对应系统能量耗散率随时间的变化曲线,如图9所示。可见不稳定点L横坐标E2+越大，系统能量耗散效率越高。

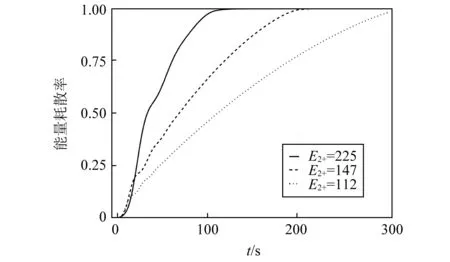
图9 系统能量耗散率与E2+的关系Fig.9 The relationship between the energy dissipation rate of the system and E2+

3 NES参数优化

3.1 不稳定点近似解

系统慢不变流形的极值点对系统是否能够触发TET有着重要影响，故求解极值点坐标是有助于NES的参数优化设计，本文通过多项式近似替换的方法，推导极值点坐标的近似表达式。

(23)

则式(20)第二式化为

(24)

式(24)对Y的一阶导数为

式(25)第一式仅在a0=0时其值为0，故非线性振子振幅小于刚度间隙时，不可能出现TET现象。

令式(25)第二式右端为0得

4k2arccos2(Y)=0

(26)

当式(26)有两个解时，式(24)存在两个极值点，满足系统能够发生TET的必要条件，令h=arccos(Y)，上式进一步化简为

(28)

式中,z为与主结构参数有关的常量，则式(24)存在两个极值点的条件为

(29)

满足上式条件时，两极值点位置对应横坐标表达式E2-,E2+如式(30)所示

(30)

将上式代入式(24)中可得到两极值点纵坐标E1-，E1+，两极值点坐标。

式(22)通过数值方法易于得到极值点坐标E2N±，与近似表达式(30)的相对误差为

(31)

如图10所示，z取0.09时统计得到表达式相对误差均值不超过5%，说明上述表达式的精度能满足工程应用的需要。

图10 极值点近似表达式的误差Fig.10 The error of the approximate expression of extreme point

3.2 优化目标

NES的能量和阻尼系数对系统能量耗散其主要作用，由式(22)第一式可知，NES能量越大，能量耗散速率越高，这可以描述为极小值点L横坐标E2+越大，系统能量耗散效率越高，如图6所示，其函数表达式为

min -E2+(a0,k,λ2)=

(32)

3.3 约束条件

3.2节的能量传递和耗散分析结果可知，为减少NES返还给主结构的能量，E1-应尽量降低。但由式(24)可知，只有当NES阻尼为0时E1-才可能为0，这种情况下振动能量会在两振子间完全的相互传递，无法耗散。本文优化目标以提高能量的耗散效率为主，为了同时兼顾能量传回的情况，将E1-作为优化模型的边界条件，设计时需要确定一个允许的能量回传的值即的E1-上限Ef，以放宽边界条件对NES阻尼λ2的限制。式(30)代入式(24)中得到函数E1-约束条件的表达式为

(33)

式中：hE2+为极小值点处的h值;Ef为可以接受的NES返还主结构的能量。

式(22)第二式存在两个极值点的约束条件

p>0

(34)

由于E1+与E2+相互耦合，触发TET的阀值E1+设计过小可能会导致系统耗散速率降低，在设计时首先需要估计NES工作时受外激励的范围，然后根据外激励的下限El进行设计，确保NES在外激励的范围内都能够有效工作

(35)

一般情况下ω0和λ1由主结构给定，其余约束条件有

(36)

3.4 优化模型

综上所述，该优化模型为

minf(a0,k,λ2)=-E2+(a0,k,λ2)

s.t.p>0

E1-

E1+

(37)

3.5 优化结果及数值仿真

通过质量感应法测得某空间光学载荷次镜处的等效单自由度主结构参数,如表1所示。

表1 主结构结构参数Tab.1 Main structure parameter

为对上述优化模型进行求解，本文选用随机搜索法对模型进行优化，随机搜索算法的工作方式是先产生一族随机初始点，然后从每个初始点用一个局部优化方法收敛到一个局部极小值，最佳局部极小值被选为问题的解。

根据空间光学载荷振动抑制的实际要求取Ef=0.03，El=0.5，z=0.082，通过数值非线性最优化对模型进行优化。表2给出了优化变量的取值范围和和优化值。

表2 变量取值与优化结果Tab.2 Optimal and original parameter values

通过龙格-库塔数值方法计算参数优化前后主结构加速度响应,如图11所示，系统能量耗散效率明显增大。结果表明本文所用的优化变量，目标，方法基本可行，优化效果比较明显。

图11 优化前后主结构加速度响应Fig.11 Acceleration response of main structure before and after optimization

4 实验验证

为验证分段线性刚度能量阱对空间光学相机的振动抑制效果，本文为根据上述优化结果，设计了分段线性刚度能量阱原理样机，如图12所示。将其安装于空间光学遥感载荷，并在冲击激励工况下对分段性刚度能量阱的振动抑制效果进行试验验证。

本文通过力锤锤击的方法对空间相机施加冲击载荷，以空间相机次镜处加速度响应衰减至90%所用时间作为判断指标，对分段线性刚度能量阱振动抑制效果进行试验，NES实际结构参数如表3所示。由于加工条件限制，刚度间隙a0取0.4 mm为最优值，并设置a0取0.2 mm进行对比。

图12 分段线性刚度能量阱机械结构图Fig.12 Mechanical structure of nonlinear energy sinks with piecewise linear stiffness

表3 分段线性刚度NES参数Tab.3 Parameter of piecewise linear stiffness NES

搭建实验平台如图13所示，分段线性刚度能量阱安装于空间相机次镜背板处，空间相机连接振动工装安装于基座上。冲击传感器安装锤击点附近，方向与激励方向相同。冲击传感器信号由模态仪采集，力锤施加冲击载荷峰值为450 N，冲击激励输入如图14所示。

图13 冲击激励工况振动试验Fig.13 Impact excitation test of NES

图14 冲击激励输入条件Fig.14 Impact excitation condition

图15 冲击载荷下测试点加速度响应Fig.15 Acceleration response of test point under impact load

次镜处加速度响应衰减至90%时所用时间，如表4所示。实验表明，安装分段线性刚度能量阱后，测试点的振动能量耗散速率有所提高，而当NES参数为优化值时，较未安装NES时主结构加速度响应衰减至90%时所用时间减少33.2%，较非最优化参数减少了26.9%。

表4 冲击实验结果Tab.4 The results of the impact test

实验结果表明，根据本文优化方法所选择的NES参数有效，NES结构参数优化后，系统能量耗散效率较未优化有明显提升。实现了通过安装分段线性刚度能量阱提升系统振动能量耗散效率的目的。

5 结 论

本文通过复变平均法推导了分段线性刚度能量阱的慢变方程，研究得到系统慢不变流形极值点坐标的近似表达式，以此建立了分段线性刚度能量阱吸振效率的优化模型，并针对某空间光学载荷进行了分段线性刚度NES的振动抑制实验，研究结果表明：

(1)冲击激励下，分段刚度能量阱慢不变流形和立方刚度能量阱类似，不稳定分支是否存在对系统能否触发TET有重要影响。

(2)通过多项式近似替代可以得到极值点的近似表达式，经过与数值方法对比，该表达式进度较高，能够满足工程应用的需要。

(3)根据极值点的近似表达式构建了NES吸振效率的优化模型，并对某空间刚光学载荷的分段线性刚度NES进行了优化设计，优化后系统达到90%能量耗散率所用时间降低了35.5%，较非最优化参数降低了26.9%。，NES结构参数优化后，系统能量耗散效率较未优化有明显提升，证明了本文所建立的优化模型是合理的。

由于机械制造等限制，本文实验结果未能完全达到参数的最优值，将会继续改进分段线性刚度能量阱机械结构的进行研究和改进。