Rayleigh波作用下饱和海床土中管桩竖向动力特性研究

牛晓波， 章 敏,2,3， 赵仓龙

(1. 太原理工大学 土木工程学院,太原 030024; 2. 华东交通大学 铁路环境振动与噪声工程研究中心,南昌 330013; 3. 浙江大学 建筑工程学院,杭州 310058)

在大部分浅源地震中，Rayleigh波(以下简称为R波)往往携带着绝大部分地震能量，引起土层竖向和水平运动，是造成建筑物破坏的主要波型。在全球范围内发生的地震中，如唐山、汶川、智利和海地大地震等，许多结构存在竖向地震破坏的迹象。在高烈度区，尤其是震中区，竖向地震力的作用非常明显。当前，我国正大力发展海洋能源的开发利用，其中相当一部分近海海洋工程建设在地震活跃的环太平洋地震带上，其安全性易受到地震威胁。对于海上桩承结构，如海上风机和钻井平台等，自振周期相对较长，加之桩顶作用较大的集中质量，强烈的竖向地震通过高幅值的拉压作用可能造成桩基础的竖向承载力和刚度快速退化，进而引发结构破坏。《建筑结构抗震设计规范》规定8度、9度区大跨度和长悬臂结构及9度区的高层建筑，应考虑竖向地震作用。

Tan[1]采用有限元法对流体-饱和半空间中R波的传播特性进行了研究。Sharma等[2]研究了流体层-饱和多孔介质中R波的频散特性，探讨了海水深度对相速度的影响。Kumar等[3-4]针对饱和土存在上覆均质和非均质双流体层时R波的频散问题进行了研究。Albers[5]基于简单混合物理论，发现土-水分界面在不同渗透性下存在漏Rayleigh波，漏Stoneley波和真Rayleigh波三类面波。Pal等[6]针对流体层-砂层-饱和半空间土地基中R波的频散特性进行了分析。Paul等[7]研究了非均质流体-砂土-饱和土-弹性土四层海洋地层模型中R波的传播特性。夏唐代等[8]基于耦合的解析法和有限元法，讨论了流体-固体介质中R波的传播规律，并与Stoneley波进行了对比。最近，仇浩淼等[9]基于Biot波动理论和等效流体模型，研究了流体-准饱和多孔介质界面Scholte波的传播特性。

对于弹性波作用下桩的竖向振动问题，Makris[10]发现R波作用下垂直运动的桩土位移差远大于水平运动。Kaynia等[11]基于Green函数，对桩-土-桩相互作用进行了分析，讨论了地震作用下桩的运动和惯性效应对桩基受力的影响。Lu等[12]基于虚拟桩法，研究了R波作用下桩顶集中质量的重力和惯性效应对单桩动力响应的影响。王海东等[13-14]和柯瀚等[15]基于 Novak 薄层法，讨论了R波作用下桩底支承条件和地基成层性对桩土竖向共同作用的影响。总的说来，目前有关R波作用下单桩竖向动力响应的研究主要局限于陆地情况，而对海洋环境中的此类问题，尚不够深入。

鉴于以上背景，本文基于流体-饱和两相介质地层模型，研究了R波作用下饱和海床土中管桩竖向动力响应，并就流体层厚度以及管桩尺寸等参数的影响进行了讨论。

1 计算模型与基本假定

图1为R波作用下饱和海床土中管桩竖向振动计算模型。其中上覆流体层厚度为Hw，管桩为摩擦桩，内外半径分别为r2和r1，壁厚t=r1-r2，桩长为L，将上部结构简化为桩顶集中质量m。坐标系原点取海床面钢管桩的圆心，z轴向下取正。

图1 计算模型Fig.1 The computing model

以下分析中引入如下假定：①海床土为均质、各向同性的饱和两相弹性介质；②海水为不可压缩、无黏性的理想流体，表面为自由边界，海床面为完全透水边界；③桩土振动为小变形，桩土接触面始终保持接触，不发生滑移和脱离，即桩土接触面的位移、应力连续，桩土接触面不透水； ④管桩简化为弹性、圆形均质空心杆，按一维杆件处理。

2 边界条件

2.1 管桩边界条件

(1)桩顶边界条件：将上部结构简化成质量为m的桩顶集中荷载，即

(1)

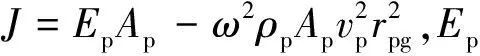
(2)桩端边界条件：考虑到R波有效传播深度大概为波长的1.5～2.5倍左右，且海上结构的钢管桩一般较长，很难接触到基岩，及钢管桩自身的横截面积小，桩端土作用力可以忽略不计，故此处将桩端假定为轴力为0的自由端，即

(2)

2.2 海水层边界及连续性条件

海水表面的动水压力为零，海床面处法向有效应力、切应力为零，且孔隙水压力、位移连续性，即

Pw(z=-Hw)=0

(3a)

τxz(z=0)=0

(3b)

Pf(z=0)=Pw(z=0)

(3c)

σz(z=0)=0

(3d)

uwz=uz+wz

(3e)

式中:Pw为海水动水压力;τxz为土层切应力;σz为土层有效应力;Hw为海水层厚度;uwz为海水竖向位移;uz为土骨架的竖向位移;wz为孔隙水的相对竖向位移。

3 方程的建立及求解

3.1 流体控制方程的求解

将海水视为不可压缩的无黏性理想流体，其运动状态可由以下Laplace方程描述

(4a)

(4b)

式中：uw为海水的矢量位移;α=1 500 m/s为水中声波波速。

(5)

Pw=[Qexp(kβz)+Pexp(-kβz)]exp(ikx-iωt)

(6)

对于以下简谐振动，推导中均略去时间因子eiωt。将式(6)代入式(4b)，同时引入流体势函数φ0，可求得海水的竖向位移uwz为

(7)

式中，φ0=(Qexp(kβz)+Pexp(-kβz))exp(-ikx)。

3.2 R波作用下自由场动力响应

将海床地基视为饱和两相弹性介质，采用Biot波动方程描述其动力特性；参照文献[16]的推导方法，引入固相以及流相势函数，对方程两边分别进行散度和旋度计算，可得

(8b)

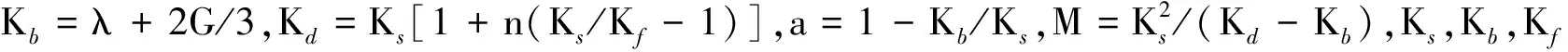
非零解，则系数行列式为0，则可得4个压缩波波数kp的解。由于R波沿深度和传播方向存在衰减，须满足imag(kp)<0。据此，可筛选出满足条件的2个压缩波波数；即可获得同一压缩波下φs与φf满足的关系

φf=E1φs

(9a)

φf=E2φs

(9b)

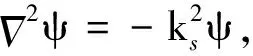
存在非零解，则系数行列式为0，即得到的1个剪切波波数ks，仅imag(kp)<0满足条件R波沿深度的衰减性；即可获得ψs与ψf满足的关系

ψf=F1ψs

(10)

即Rayleigh波势函数可表示为

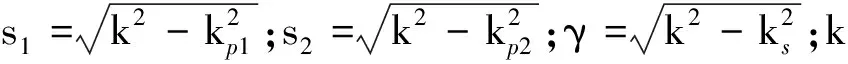
uz=-s1A1exp(-s1z-ikx)-s2A2exp(-s2z-ikx)-

ikC1exp(-γz-ikx)

(12a)

wz=-s1A1E1exp(-s1z-ikx)-s2A2E2exp(-s2z-ikx)-

ikC1F1exp(-γz-ikx)

(12b)

对于轴对称问题，饱和土中的物理方程为

(13a)

(13b)

pf=-αMe-Mζ

(13c)

将式(12)分别代入式(13a)～式(13c)，可得正应力、剪应力以及孔隙水压力分别为

(14a)

(14b)

(14c)

将以上三式代入边界条件式(3a)～式(3e)，可得

(15)

为使上述奇次方程存在非零解，系数矩阵的行列式应为0，可求得饱和土中R波波数k。由于R波的衰减特性，要求imag(k)<0，real(s)>0，real(γ)>0，据此可筛选出满足条件的R波波数。

3.3 管桩竖向振动响应

参照王海东等的推导方法，可得桩周土和桩芯土的竖向动阻抗Cs1,Cs2分别为

Cs1=2πr1GhK1(hr1)/K0(hr1)

(16a)

Cs2=2πr2GhI1(hr2)/I0(hr2)

(16b)

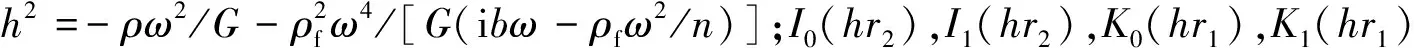
根据式(12)，桩周(芯)土的竖向平均位移us为

us|x=r1/r2=(1-n)uz+nWz=uz+n(Wz-uz)=

uz+wz

(17)

式中:wz为孔隙水相对于土骨架的竖向位移;uz,Wz分别为土骨架以及孔隙水的竖向绝对位移。饱和土作为两相混合介质，其竖向平均位移实际为土骨架和孔隙水两者竖向位移的体积平均。

对于大直径钢管桩，考虑其竖向振动下的横向惯性效应，则桩的竖向振动微分方程为

Cs2(us2-up)=0

(18)

式中，us1,us2分别为桩周土和桩芯土竖向平均位移。

上述方程可整理得

(19)

上述方程的通解为

(20)

式中，A,B为由边界条件确定的待定系数。

令其特解为

(21)

将式(21)代入式(19)，可得

(22a)

(22b)

(22c)

故式(19)的解

up=Aexp(Λz)+Bexp(-Λz)+Cexp(-s1z)+

Dexp(-s2z)+Sexp(-γz)

(23)

根据边界条件式(1)和式(2)，可得

(ΛJ+mω2)A+(mω2-ΛJ)B=(s1J-mω2)C+

(s2J-mω2)D+(γJ-mω2)S

(24a)

AΛexp(ΛL)-BΛexp(-ΛL)=Cs1exp(-s1L)+

Ds2exp(-s2L)+Sγexp(-γL)

(24b)

联立以上两式，可求得系数A,B的值，则管桩竖向位移可最终表示为

up=Aexp(Λz)+Bexp(-Λz)+Cexp(-s1z)+

Dexp(-s2z)+Sexp(-γz)

(25)

4 算例分析

4.1 解的退化验证

为验证上述理论推导的正确性，将本文结果与Tan的结果进行对比；同时令上覆海水厚度Hw=0.01 m，r2=0.01 m，将流体-半空间模型退化到半空间土中实心桩的情况，将本文结果与Lu等的结果进行对比。其中，Tan研究中的地基土参数：土层参数为ρs=1 000 kg/m3，ρw=1 000 kg/m3，Ks=36 GPa，Kf=2.1 GPa，n=0.3，μ=0.25，G0=10 MPa，kd=10-4m/s；海水深度Hw=375 m；频率f=1 Hz，m=0.01 kg。图2为R波作用下上覆流体层以及土体水平、竖向位移随深度的分布曲线。Lu等研究中的地基土参数：土层参数为ρs=2 700 kg/m3，Ks=36 GPa，Kf=2.1 GPa，n=0.3，l=0.05，G0=10 MPa，kd=10-4m/s；实心桩参数为r1=0.5 m，L=40 m ；其他参数为f=5 Hz，Ff=1 000 kN，其中Ff为桩顶集中力。图3为桩身轴力随深度的分布，并与Lu等的结果进行对比。

从对比结果来看，图2的差异可能来自于地基土模型，原文为流体-单相土模型，海床面孔压不连续，而本文采用流体-饱和土模型，能反映土-水分界面处水压与孔压的连续性，结果更为合理。图3桩身最大轴力与对比文献存在一定差异，但规律基本一致。图3的差异可能来自于计算方法的不同，原文基于三维Green函数，而本文基于Winkler 地基梁模型。总的说来，以上对比基本验证了本文理论推导的正确性。

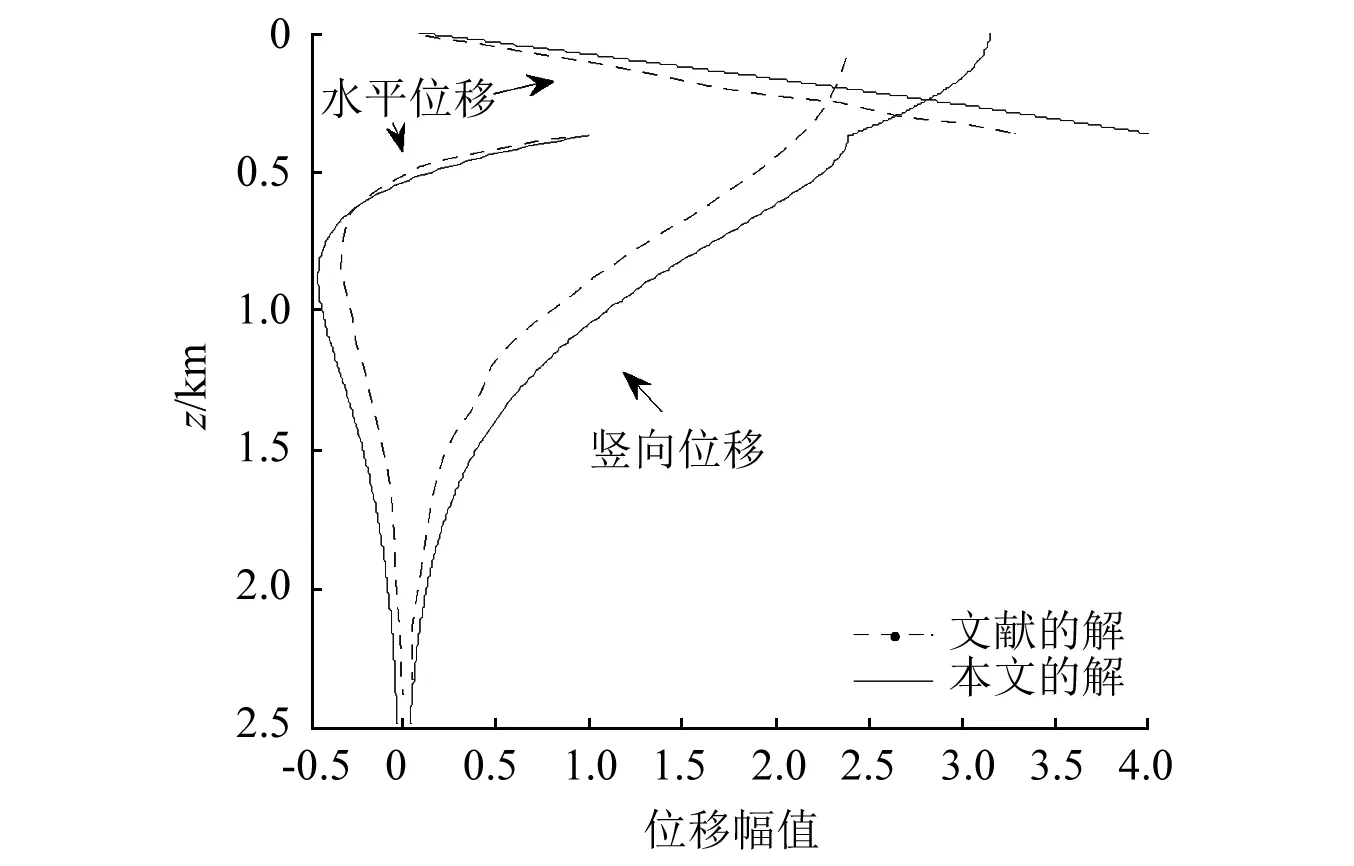
图2 流体-半空间土水平及竖向位移的对比Fig.2 The comparison of horizontal and vertical displacement of fluid fluid half space

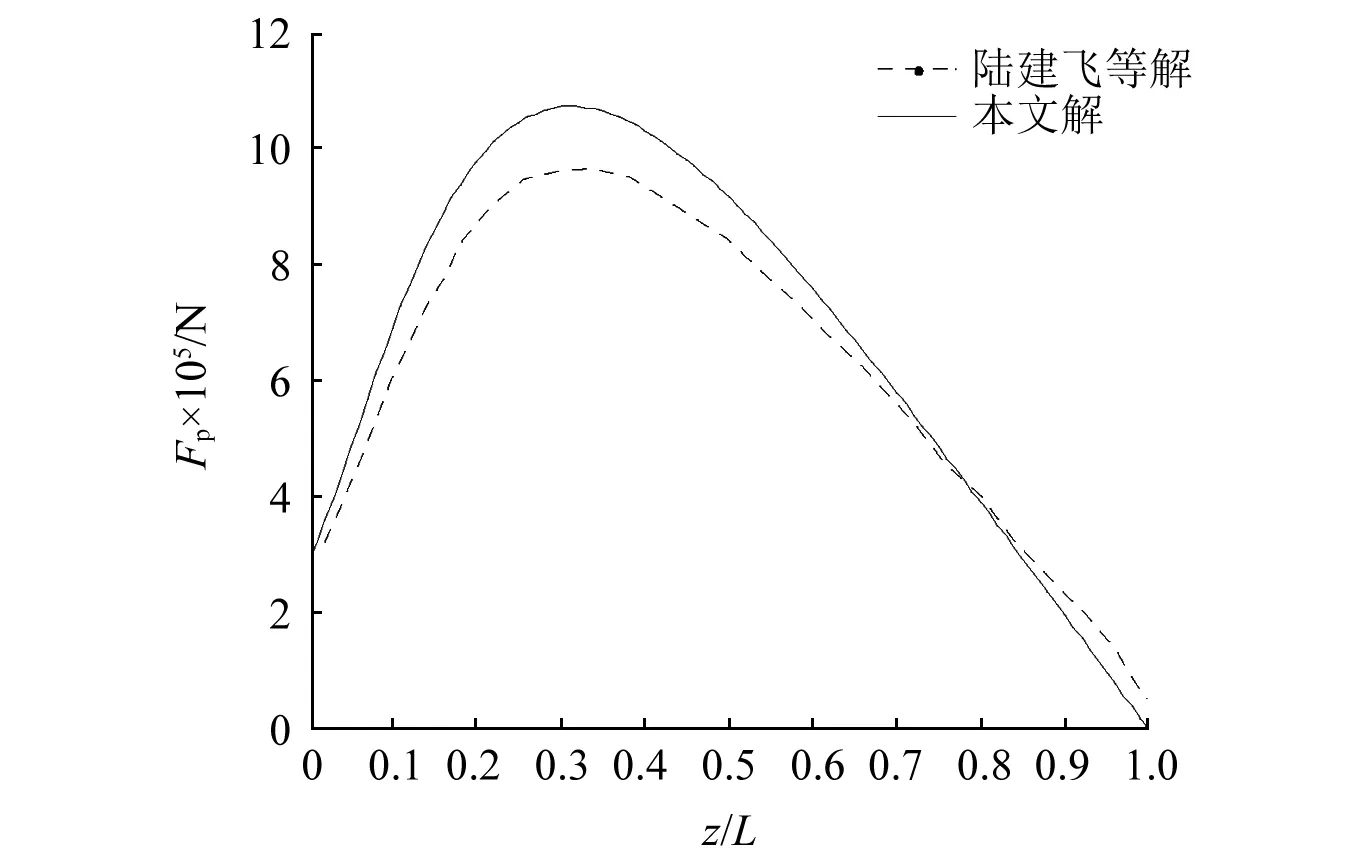
图3 桩身轴力的对比Fig.3 The comparison of the axial force of the pile

4.2 参数分析

以下就不同参数对管桩竖向动力响应的影响进行讨论。其中，桩周土与桩芯土的参数一致，且考虑到海洋工程大多属于高耸结构，一阶共振频率往往较小，高阶振动衰减较快，以下分析中取频率f=2 Hz。若无特殊说明，计算参数如下：海水层参数为Hw=10 m，ρw=1 000 kg/m3，Kf=2.1 GPa；海床土参数为n=0.3，μ=0.25，Ks=36 GPa，ρs=2 000 kg/m3，l=0.05，G0=10 MPa，kd=10-4m/s；钢管桩参数为r1=2 m，r2=1.96 m，L=30 m，ρp=7 900 kg/m3，Ep=210 GPa；其他参数为f=2 Hz，m=150 t。

图4为不同海水厚度下海水-海床土竖向位移沿深度的分布。图中z=0为海床面，横轴为竖向位移Up/A1，其中A1为固相的旋转势函数幅值(见式(19))。从图中可以看出，在同一流体厚度下，随着深度的增加，流体层竖向位移实部及虚部均逐渐增大，土层竖向位移实部在海床面附近达到峰值，并沿着土层深度最终趋于0，而虚部则沿深度持续减小，其大小远小于实部。值得说明的是，流体层位移分布规律受饱和土密度的影响较大。如图2所示，当土骨架密度为1 000 kg/m3时(Tan研究中的参数)，流体层竖向位移随着深度的增加逐渐减小，曲线斜率在海床面处存在不连续，而对于本算例(土骨架密度为2 000 kg/m3)，流体层竖向位移随着深度的增加而增大，曲线则光滑连续。其随着流体层厚度的增加，流体层和土层的位移均呈现出减小的趋势，流体层表面竖向位移则逐渐趋近于0，海床面附近的土体位移峰值的位置略有上移。图4(a)中的附图进一步给出了海床表面竖向位移随流体层厚度的变化。从图中可看出， 随着流体层厚度Hw的增加，海床表面竖向位移逐渐减小，当Hw超过10 m时，则基本保持不变。这主要是由于R波在传播过程中部分能量将向海水中耗散，从而导致海底竖向地震响应减小。

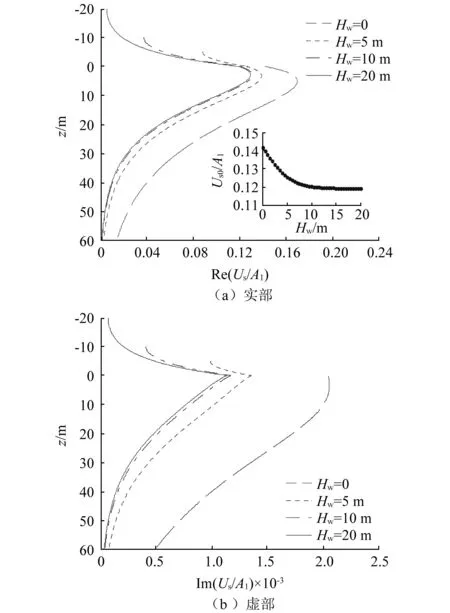
图4 海水厚度对海水-海床土竖向位移的影响Fig.4 The effect of seawater thickness on vertical displacement of fluid-soil

图5为不同海水厚度下动水压力及孔隙水压随深度的分布。由图可知，在同一流体厚度下，流体动水压力朝海水面方向逐渐降低，而流体厚度的变化对土层孔隙水压力的影响很小。局部放大图可进一步得知，土体孔隙水压力在海床表面以下0.4 m处达到峰值，朝海床面方向，则急剧减小至海水动压力，沿土体深度方向则逐渐减低，大致在海床面以下30 m处降至0。图6为不同水深处动水压力随频率的变化。由图可知，随着频率的增加，动水压力先增大至峰值，后逐渐减小至0；且随着与海床面距离的减小，其峰值及衰减至0时的频率均随之增大。

图5 海水厚度对动水压力及孔隙水压的影响Fig.5 The effect of seawater thickness on hydrodynamic pressure and pore water pressure

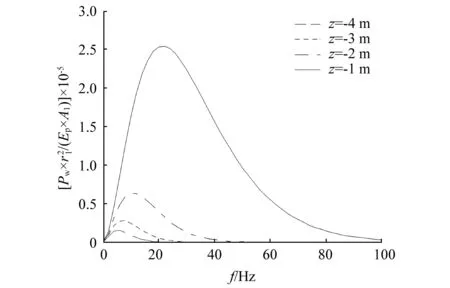
图6 不同水深处动水压力随频率的变化Fig.6 The variation of hydrodynamic pressure with frequency at different water depths

图7为不同桩长下桩顶竖向位移随海水厚度的变化。可知，随着海水厚度和桩长的增加，桩顶位移逐渐减小，当海水层厚度超过10 m时，位移不再变化。由于钢管桩刚度较大，桩身位移主要由桩端土压缩引起，本身的压缩变形很小，即桩顶与桩底的位移相差很小。图8为桩顶位移随桩径的变化，其中管桩壁厚t=40 mm。由图可知，随着桩径的增加，桩顶位移逐渐减小，尤其是桩顶集中质量m较大时，降幅尤为明显。但随着管径的进一步增大，桩顶质量的影响逐渐减弱，不同m下的位移最终趋于同一数值。

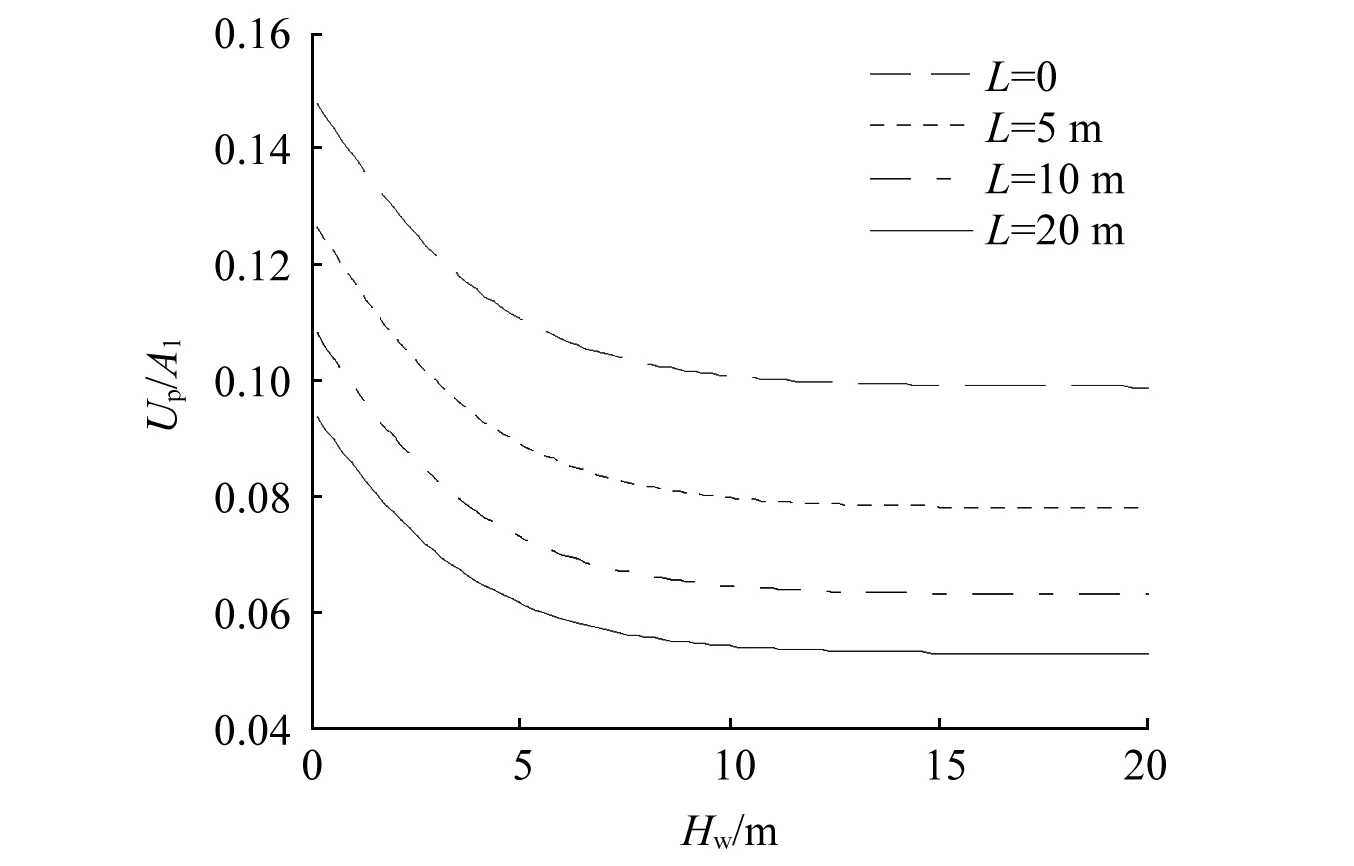
图7 海水厚度对桩顶竖向位移的影响Fig.7 The effect of seawater thickness on vertical displacement of pile top

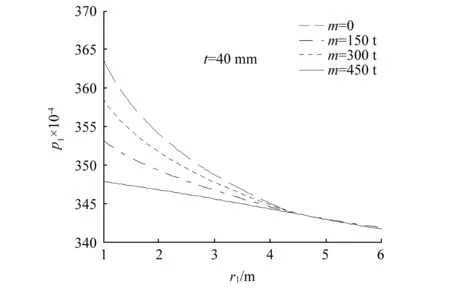
图8 桩顶竖向位移随管桩桩径的变化Fig.8 The variation of vertical displacement of pile top with the diameter of pipe pile

图9(a)和图9(b)分别为不同桩长及土体剪切模量对桩侧摩阻力的影响。由图9(a)可知，在海床面附近，桩侧摩阻力存在一峰值，且桩长越长，数值越小。此后，随着深度的增加，桩侧摩阻力逐渐减小。试算发现，管桩内壁摩阻力仅为外侧的1/10，基本可忽略不计。由图9(b)可知，在海床面以下2.5倍波长范围内(从图18(a)中得知波长为12 m左右)，桩侧摩阻力随土体剪切模量的增大而减小；当深度超过2.5倍波长时，土体剪切模量的影响很小，摩阻力分布曲线基本重合。图10为不同海水层厚度下桩土竖向位移差随深度的分布。可如，随着海水层厚度的增加，位移差整体减小，但影响逐渐减弱。

图11和图12分别为不同管桩壁厚下桩身轴力和竖向位移随深度的分布。由图11可知，随着深度的增加，管桩轴力呈现出先增大后减小的趋势。管桩壁厚对桩身轴力的影响很小，仅在轴力峰值处，随着壁厚的增加而有所增加。当增加桩顶集中质量时，桩身中上部轴力相应增加。由图12可知，管壁越薄，即管桩的轴向刚度越小，桩顶与桩底的位移差越大。此外，桩顶集中质量的存在，使桩身位移整体增大。图13进一步给出了桩顶位移随管桩壁厚的变化，其中管桩外径r1为2 m。由图可知，随着壁厚的增加，桩顶位移逐渐减小，超过50 mm后则基本保持不变，且桩顶集中质量越大，壁厚对桩顶位移的影响相对越明显。

图14(a)和图14(b)分别为不同桩径和桩长条件下桩身轴力随深度的分布。由图14(a)可知，随着桩径的增加，同一深度处管桩轴力逐渐增大。图14(b)可以发现，桩长越长，管桩轴力越大，轴力峰值位置逐渐下移，而不同桩径对应的峰值位置则基本相同。

图9 桩侧摩阻力随深度的分布Fig.9 The distribution of pile side friction with depth

图10 海水厚度对桩土位移差的影响Fig.10 The effect of seawater thickness on displacement difference between seabed soil and pile

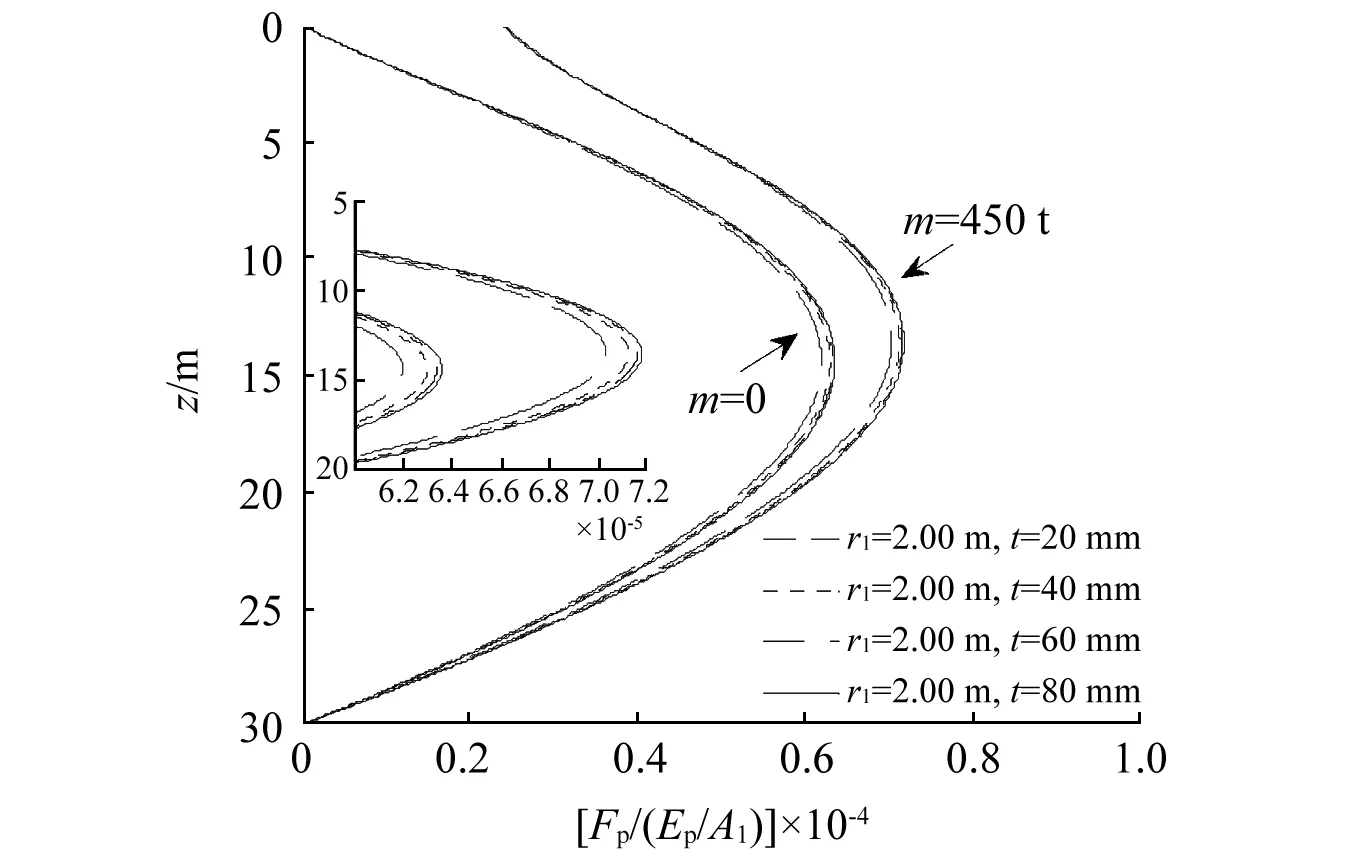
图11 管桩壁厚对桩身轴力的影响Fig.11 The effect of pipe pile wall thickness on axial force of pile body

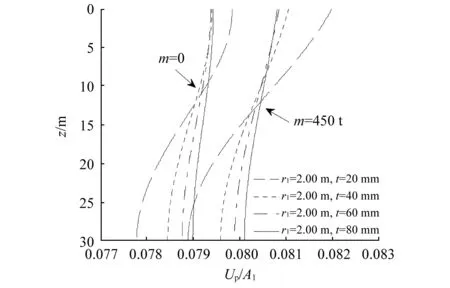
图12 管桩壁厚对桩身竖向位移的影响Fig.12 The effect of pipe pile wall thickness on vertical displacement of pile body

图14 桩身轴力随深度的分布Fig.14 The distribution of axial force of pile shaft with depth

图15(a)和图15(b)分别为横向惯性效应(主要体现在桩的泊松比上)对混凝土实心桩和钢管桩桩顶竖向位移的影响。其中图15(a)的计算参数为：半径r=1 m，桩长L=15 m，密度ρp=2 500 kg/m3，弹性模量Ep=1 000Es。由图可知，频率f<400 Hz时，不同泊松比所对应的曲线基本重合，即泊松比对桩顶位移基本不产生影响；当频率f>400 Hz时，泊松比的影响开始显现，表现为泊松比越大，桩顶位移越大，但随着频率的进一步增大，其差异又逐渐减小。而对于钢管桩(见图15(b))，在整个频率范围内，不同泊松比所对应的曲线几乎完全重合。这主要是因为钢管桩的弹性模量远大于混凝土，泊松比的影响比重很小。

图16不同深度处海床土竖向位移随频率的变化规律，其中图16(a)右纵轴中λ为R波波长。由图可知，随着频率的增加，土体竖向位移的实部和虚部均先增大后减小，并最终趋于0；且深度越大，衰减速率也越快。这反映了R波作为面波在深度方向的衰减性。同时图16(a)还给出了R波波长随频率的变化曲线。可知，波长随频率的增加逐渐降低，超过75 Hz后基本衰减为0。此外，图中也可看出，对于某一深度，如z=5 m，土体位移衰减至0所对应的频率约为30 Hz，该频率所对应的波长为2 m左右，即R波的有效传播深度约为2.5倍波长，高于单相弹性介质中1.5倍波长，其他3个位置的比例系数也大致在2.5左右。这表明饱和两相地基中R波的影响深度明显高于单相弹性地基。

图15 桩顶位移随频率的变化Fig.15 The variation of pile top displacement with frequency

图16 海床土竖向位移随频率的变化Fig.16 The variation of vertical displacement of saturated soil with frequency at different positions

图17为不同土体孔隙率下海床面竖向位移随渗透系数的变化。由图可知，位移实部在kd小于一定值时保持不变，当大于其值时，则随着kd的增加逐渐减小并趋于稳定；而虚部在整个渗透系数范围内出现了一次上下波动，并趋于稳定。孔隙率在频率较高时(f=10 Hz)对位移的影响较大，表现为，随着孔隙率的增加，位移实部逐渐减小，而位移虚部的影响主要体现在曲线的波动峰值区域。

图17 海床面竖向位移随渗透系数的变化Fig.17 The effect of Darcy′s permeability coefficient on vertical displacement of seabed surface

5 结 论

本文围绕Rayleigh波作用下饱和海床中管桩的竖向动力响应进行研究，通过算例分析，得到了如下结论：

(1)随流体层厚度的增加，海床及管桩竖向位移均逐渐减小，当流体层厚度超过10 m，则基本保持不变。

(2)动水压力和海床竖向位移均随频率的增加表现为先增大后逐渐降至0的趋势；且随着水深位置的增加，动水压力峰值及衰减至0时的频率均随之增大。

(3)随着桩径的增大，不同桩顶质量下的管桩竖向位移逐渐减小，最终趋于同一数值。

(4)横向惯性效应对于大直径混凝土桩的高频振动存在一定影响，而对于钢管桩则基本可以忽略。