基于自适应混合结构的快速收敛函数链接人工神经网络算法研究

李欢欢

(牡丹江师范学院 图书馆，黑龙江 牡丹江 157011)

随着生活水平的不断提高，人们更加期望舒适、安静的环境。但是如今的噪声污染问题使得这一任务变得更加艰巨。强烈的噪声会对人们的听力系统、神经系统和消化系统等造成一定的损伤。我军平战时的数据表明：高炮兵、装甲兵的声损伤发病率约为23.5%～48.3%，因声损伤致残约占评残总数一半[1]。为有效降低噪声的影响，最初的解决方案是利用声音与声学材料或声学结构相互作用进行噪声控制，称为被动噪声控制技术。在被动噪声控制中，吸声材料的体积与噪声波长成正比。所以对于低频噪声，被动噪声控制装置的体积就会变的极其庞大，增加了设备成本。此外，被动噪声控制技术的降噪频带比较窄，各频率的吸声系数固定，不具有自适应特性，无法有效降低时变噪声。为适应更加复杂噪声环境，提高降噪效果，主动噪声控制(active noise control, ANC)技术应用而生。

ANC系统是基于声波相消干涉原理的电声学装置，主要包含参考传声器、次级扬声器、误差传声器和自适应控制器[2-3]。参考传声器用来测量待处理的噪声信号，次级扬声器产生一个与待处理噪声幅度相同、相位相反的声音信号，误差传声器采集声音叠加后的残余误差信号，自适应控制器用来控制次级扬声器产生合适的次级噪声。随着高速信号处理技术的不断发展， ANC技术的应用更加多样化，各式各样的ANC控制算法脱颖而出，其中基于线性有限脉冲响应(finite impulse response, FIR)结构的滤波-X最小均方误差(filtered-X least mean square, FXLMS)算法就是最流行的算法之一[4-5]。但是在实际ANC系统应用中，信号的传输路径可能具有非线性特性[6]，如电子器件老化、扬声器饱和、较强声压声音在管道中传播等。此时，这种线性控制算法的降噪效果就会变差，甚至失效。因为FIR滤波器不具备描述非线性模型的能力。

为了解决ANC的非线性问题，许多优秀的非线性控制方法被提了出来[7-8]，主要分为两类：人工神经网络和多项式滤波器，分别以函数链接人工神经网络(functional link artificial neural network, FLANN)[9-12]和基于沃尔泰拉(Volterra)滤波器的FXLMS(VFXLMS)算法为代表[13-14]。FLANN利用三角函数展开拟合非线性模型。这种拟合具有广泛的适用性，但不具有明确针对性，限制了FLANN的收敛速度，需经过较长时间进行精确拟合。Volterra滤波器为常见的非线性模型，可以完整表征多数非线性系统，因此VFXLMS收敛速度较快。但是Volterra滤波器的拓展阶数需要先验知识进行设定，而实际的非线性系统模型阶数往往是未知的，因此容易产生偏差，限制VFXLMS的降噪效果。此外，VFXLMS计算量偏大，很难满足实际应用需求。为了缓解VFXLMS中的缺陷，研究学者提出了基于双线性(Bilinear)滤波器的FXLMS(BFXLMS)[15-17]。BFXLMS采用非线性递归结构，继承了VFXLMS的收敛优势，但是不受拓展阶数的限制，且计算量少。与FLANN算法相比，BFXLMS收敛速度快，但是降噪性能较差。

基于上述原因，本文对BFXLMS和FLANN进行有效结合，提出了一种新的ANC算法——CBFLANN(combined bilinear FLANN)。在相同参数条件下，该算法同时继承了BFXLMS收敛速度快和FLANN降噪量大的优势。

1 FLANN算法降噪原理介绍

基于FLANN算法的非线性ANC系统，如图1所示。从图中可以看出，在FLANN算法中，首先将输入信号以正弦方式进行非线性拓展。然后将拓展的结果利用线性滤波器组进行处理，每组滤波器处理后的结果为yi(n)，表示为

yi(n)=Hi(n)Vi(n)T，i=1,2,…,2P+1

(1)

式中，P为函数拓展的阶数，其中

Hi(n)=[hi,0(n),hi,1(n),…,hi,N(n)]

(2)

图1 基于FLANN算法的非线性ANC系统Fig. 1 Nonlinear ANC system based on FLANN algorithm

V1(n)=[x(n),x(n-1),…,x(n-N)]

⋮

V2P(n)=[sin(Pπx(n)),…,sin(Pπx(n-N))]

V2P+1(n)=[cos(Pπx(n)),…,cos(Pπx(n-N))]

(3)

式中，N为滤波器存储阶数。次级输出表示为

(4)

在FLANN算法中，线性滤波器组的权重更新为

(5)

(6)

e(n)=p(n)-d(n)

(7)

(8)

将式(1)～式(3)代入式(4)得

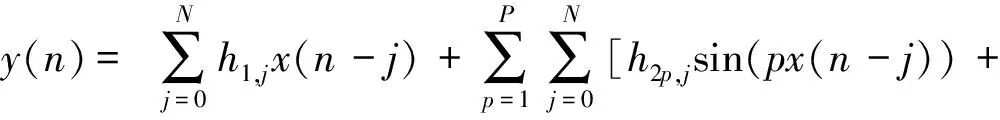
(9)

从式(9)可以看出，等式右边第一项为线性控制，第二项为非线性控制。由三角函数的麦克劳林展开得

(10)

(11)

此时，式(9)非线性控制部分可进一步写成

(12)

将式(9)式(12)代入式(8)，此时次级噪声可以表示为

(13)

在ANC系统中，初级路径一般都是连续的函数，因此总是可以通过Volterra模型表示为

(14)

式中：T(T>1)为非线性声学路径的阶数；hr(k1,…,kr)和K+1分别为第r个非线性多项式的系数和采样长度。对比观察式(13)和式(14)可知，FLANN算法是利用三角函数的非线性展开拟合非线性初级噪声。这种拟合具有广泛的适用性，但不具有明确针对性，限制了FLANN的收敛速度，需经过较长时间进行精确拟合。

2 CBFLANN算法设计与分析

由上述分析可知，在非线性ANC系统中，FLANN具有良好的降噪量，只是收敛速度欠佳。BFXLMS采用非线性多项式滤波器作为控制器，对初级噪声中各非线性部分具有明确针对性，因此收敛速度较快。为了提高FLANN的收敛速度，利用自适应混合参数将FLANN和BFXLMS进行并行凸组合，提出了CBFLANN算法，如图2所示。通过混合参数的调节，使CBFLANN在收敛过程中降噪性能主要依赖于BFXLMS，而在接近稳态时，降噪性能主要依赖于FLANN。因此与FLANN相比，CBFLANN采用了BFXLMS的收敛速度，加快了收敛过程。提出的CBFLANN具体设计过程如下。

图2 提出的CBFLANN算法Fig.2 Diagram of the proposed CBFLANN algorithm

在提出的CBFLANN中，次级输出表示为

y(n)=λ(n)yb(n)+(1-λ(n))yf(n)

(15)

式中：yf(n)为FLANN的输出；yb(n)为BFXLMS的输出；λ(n)为[0,1]区间内的自适应参数，其表达式为

(16)

FLANN的输出yf(n)如式(1)～式(4)所示。Bilinear拓展表示为

G1(n)=[x(n),x(n-1),…,x(x-N)]

G2(n)=[y(n-1),y(n-2),…,y(n-N)]

(17)

其输出为

yb(n)=A(n)G1(n)T+B(n)G2(n)T+C(n)G3(n)T

(18)

其中，

(19)

定义

H(n)=[H1(n),H2(n),…,H2P+1(n)]T

(20)

为FLANN权重向量

W(n)=[A(n)B(n)C(n)]T

(21)

为BFXLMS权重向量。

在CBFLANN算法中，权重向量H(n)和W(n)分别进行独立更新。定义

(22)

(23)

式中，E[·]为获取信号的期望值。

(24)

为FLANN独立作用时产生的估计误差噪声

(25)

(26)

其中，

(27)

xf(n)=[V1(n),…,V2P,V2P+1(n)]T

(28)

W(n)更新表达式为

(29)

其中，

(30)

xb(n)=[G1(n)G2(n)G3(n)]T

(31)

自适应混合参数λ(n)通过调整α(n)进行实时控制，以获得更佳消噪效果。α(n)同样通过LMS算法进行更新。定义

ξ(n)=E[e2(n)]

(32)

式中，误差信号e(n)表达如式(7)所示，不同的是此时次级输出y(n)不再是单一的FLANN输出，而是FLANN与BFXLMS的有效结合。α(n)通过式(33)更新

(33)

其中，

(34)

为FLANN与BFXLMS的次级路径估计滤波差分输出。

观察式(15)、式(16)以及式(33)可知，混合参数λ(n)是一个实时变化的量，其取值决定于CBFLANN的总体误差e(n)以及BFXLMS和FLANN的输出差值yb(n)-yf(n)，类似于一个软开关，通过改变BFXLMS和FLANN输出的作用强度，得到最后输出。这意味着CBFLANN的输出通过混合参数在同一时刻趋向于选取BFXLMS和FLANN的最优值，有望实现BFXLMS收敛性能和FLANN降噪量的有效结合。

3 仿 真

以上分析表明，通过自适应混合参数的调节，提出的CBFLANN有望实现BFXLMS和FLANN的优势互补，同时具有BFXLMS的收敛速度和FLANN的降噪量。为进一步验证，在不同初级路径与不同信噪比的参考噪声环境下，将提出的CBFLANN与FXLMS，BFXLMS以及FLANN进行比较，其中FLANN采用一阶拓展，即P=1。比较结果采用归一化均方误差(NMSE)

(35)

S(z)=z-2+1.5z-3-z-4

(36)

次级路径估计通过离线训练的方式获得，训练的信号为高斯白噪声，最终取其稳态时3 000个点的均值作为次级路径估计的系数。次级路径估计时的参数设置如表1所示。

表1 次级路径估计参数设置

3.1 仿真一

在该仿真中，参考信号x(n)为200 Hz正弦信号，信噪比为20 dB。初级路径为

p(n)=x(n)+0.8x(n-1)+0.3x(n-2)+

0.4x(n-1)x(n-3)-

0.8x(n)x(n-1)+0.9x(n)x(n-2)+

0.7x(n)x(n-1)x(n-3)

(37)

各算法的降噪效果如图3～图5所示。其中：图3为稳态时的频域结果；图4为NMSE结果；图5为各算法的误差信号和参数λ(n)的控制曲线。观察图3可知，参考噪声经过初级路径后可以产生200 Hz，400 Hz和600 Hz三种频率。FXLMS只对200 Hz噪声成分具有明显消噪效果，对400 Hz和600 Hz噪声成分没有消噪作用。BFXLMS对200 Hz和400 Hz噪声成分都具有明显消噪效果，但是对600 Hz噪声成分的降噪效果较弱。FLANN和CBFLANN对三个频率成分都有明显的降噪效果，且降噪量基本一致。这说明提出的CBFLANN继承了FLANN降噪量大的优势。这一结论在图4和图5中的稳态结果中均有体现。观察图4和图5中各算法的收敛特性，可知提出的CBFLANN具有与BFXLMS相同的初始收敛速度，比FLANN的收敛速度快。这说明CBFLANN也继承了BFXLMS收敛速度快的优势，优于FLANN。基于以上所述，FXLMS，BFXLMS，FLANN以及CBFLANN的降噪效果对比结果如表2所示。提出的CBFLANN既收敛速度快，又稳态误差小。

图3 20 dB各算法频域降噪结果Fig.3 De-noising performance of each algorithm for 20 dB in frequency-domain

图4 20 dB各算法NMSE收敛曲线Fig.4 NMSE learning curve of each algorithm for 20 dB

表2 降噪效果比较

产生上述效果的原因可以通过观察图5中λ(n)的控制曲线得知。初始状态时，λ(n)的值趋近于1，观察式(15)可知此时CBFLANN的降噪效果主要取决于BFXLMS。之后λ(n)的值逐渐接近于0，此时CBFLANN的降噪效果主要取决于FLANN。整个过程是根据误差信号调节的自适应过程，通过式(16)和(33)计算得到。同时由此可知，参数λ(n)的变化趋势直接影响CBFLANN的收敛速度和最终的稳态误差。

图5 20 dB各算法误差信号及混合参数λ(n)的变化曲线Fig.5 Error noise of each algorithm and the learning curve of mixing parameter λ(n) in 20 dB

3.2 仿真二

在该仿真中，参考信号频率及初级路径与仿真一设置相同，信噪比变为40 dB。此时，各算法的降噪效果如图6、图7和图8所示，与仿真一结果类似。FLANN和CBFLANN拥有相同的稳态误差，优于BFXLMS和FXLMS。但是CBFLANN的收敛速度却明显快于FLANN。在信噪比40 dB时，与20 dB的降噪效果相比，各算法的降噪量都有极大提高。这说明，在非线性ANC系统中，窄带参考噪声比宽带参考噪声更加容易实现噪声消除。

观察图6可知，BFXLMS、FLANN以及CBFLANN的稳态误差频谱中包含了目标频率成分以外的频率，如800 Hz，1 000 Hz，1 200 Hz，1 400 Hz等。这是因为BFXLMS中的乘积项x(n-i)y(n-j)和FLANN中的三角函数项{sin(pπx(n)),cos(pπx(n))}都可展开成无限个非线性多项式。这种现象在一定程度上会影响非线性ANC系统的降噪效果。改变步长参数，该问题会得到缓解，但却无法根本消除。而且在不同信噪比参考噪声中，该影响也不相同，如20 dB中BFXLMS和FLANN的降噪结果中这种高阶非线性噪声就明显较少。

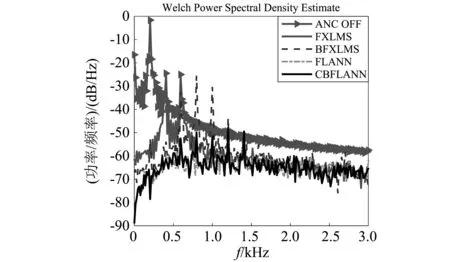
图6 40 dB各算法频域降噪结果Fig. 6 De-noising performance of each algorithm for 40 dB in frequency-domain

图7 40 dB各算法NMSE收敛曲线Fig.7 NMSE learning curve of each algorithm for 40 dB

3.3 仿真三

在该仿真中，参考信号为200 Hz正弦信号，信噪比为40 dB。初级路径的传递函数变为一个三阶多项式模型

p(n)=u(n-2)+0.08u2(n-2)-0.04u3(n-2)

(38)

式中：u(n)为参考信号x(n)与函数f(n)的卷积结果，f(n)为传递函数F(z)的脉冲响应，F(z)的表达式为

F(z)=z-3-0.3z-4+0.2z-5

(39)

图8 40 dB各算法误差信号及混合参数λ(n)的变化曲线Fig.8 Error noise of each algorithm and the learning curve of mixing parameter λ(n) in 40 dB

各算法仿真结果如9图所示，其中图9为NMSE结果，图10为参数λ(n)的变化曲线。观察图9可知，在该仿真环境下，FXLMS收敛速度最快，但是降噪效果最差；BFXLMS收敛速度次之，降噪效果与FXLMS几乎相同；FLANN收敛速度最慢，降噪效果最好；CBFLANN同时拥有BFXLMS的收敛速度和FLANN的降噪量。

通过以上三个仿真结果讨论，可知提出的CBFLANN同时继承了BFXLMS收敛速度快和FLANN降噪量大的优势，解决了传统算法快速收敛与低稳态误差二者不可兼得的问题。

图9 NMSE学习曲线Fig.9 NMSE learning curves

图10 混合参数λ(n)的变化曲线Fig.10 Learning curve of mixing parameter λ(n)

4 结 论

本文介绍了FLANN在非线性ANC系统中的降噪原理，并分析了其收敛速度慢的原因。为有效提升FLANN的收敛性能，本文利用自适应混合参数将BFXLMS和FLANN进行并行凸组合，提出了CBFLANN算法。利用混合参数实时调节BFXLMS和FLANN的作用强度，使CBFLANN同时继承了BFXLMS收敛速度快和FLANN稳态误差小的优势。不同参考信号和声学路径的仿真实验也充分验证了提出CBFLANN在非线性ANC系统中的降噪优势。CBFLANN的研究也为解决同一个ANC系统不能同时兼顾收敛速度和稳态误差的问题提供了新思路。因为CBFLANN是两个独立系统的并行组合，在实际应用中可以采用双核控制器进行实现，不会降低原有独立系统的降噪效率。