遗传算法的火电厂负荷优化

山西鲁能河曲发电有限公司 岳巨恒

为了优化火电厂的负荷分配，以便提高机组的安全性、可靠性。本文提出了以供电煤耗作为目标函数，并考虑到包含功率平衡和响应速度等约束条件，煤耗特性的拟合则利用了最小二乘法，最后求得了准确的发电机组负荷和煤耗关系。采用无回放余数随机选择操作策略的遗传算法作为本课题的求解方法，并且采用随机生成的方式生成初始种群，接着采用适用度比例法生成遗传算子，最后使本课题得解。

当实行厂网分开后，各个发电企业就必须根据厂内每个机组的特性，综合机组的安全性和经济性等各方面的因素，科学合理的安排机组间的组合和负荷分配。所以，研究火电厂的负荷优化分配十分必要。本文主要针对目前电网负荷运行状态下，各火电厂如何根据电网分配下来的负荷指令对厂内各机组的负荷安排，通过对机组煤耗特性曲线的拟合，通过与等微增率法的对比，采用无回放余数随机选择操作策略的遗传算法来使问题得到解决。

1 煤耗特性曲线的确定

1.1 机组负荷优化分配模型的确定

我们以单元机组作为研究对象，分析电力机组的煤耗量和发电量的关系并绘制其关系曲线，以便为机组的负荷优化奠定基础。选取供电煤耗作为火力电厂负荷优化分配的所建数学模型的目标函数，机组负荷优化问题可以用非线性混合整数的优化来表示。

目标函数为：

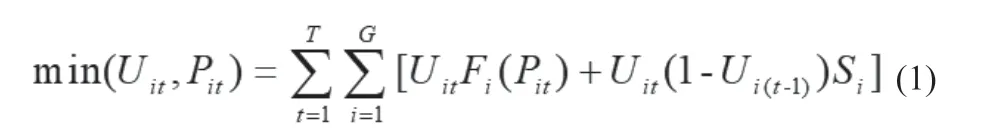
式(1)中：G为组合数，T为调度周期内的时段数；Uit=0时机组停机，Uit=1时机组运行；Pit为机组在t时段的功率变量，Fi(Pit)为发电机组在此时刻的煤耗，Si为机组启机要消耗的煤量。

部分约束条件如下：

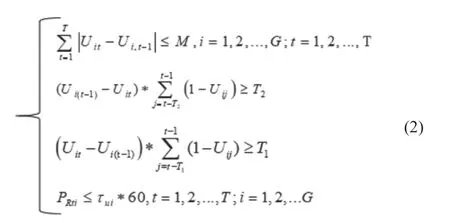
式(2)中：G为机组台数，T为调度周期内的时段数，M是机组在一个调度周期内保证机组正常运行的启停次数上限，T1为周期内每台机组的连续停运时间下限、T2为调度周期内每台机组的连续运行时间，PRti为每台机组的旋转备用容量。

1.2 煤耗特性曲线的确定

要实现火电厂机组优化分配必须绘制出准确的电力机组的煤耗特性曲线。因此，只有实际地采集电力机组工作时的各种数据才能实时绘制出准确的煤耗特性曲线，由此计算出机组的煤耗量和供电量。为了保证机组负荷在优化后的分配结果是正确可靠的，首先要根据机组负荷与煤消耗量之间的关系来确定煤耗特性曲线。工程上常用的煤耗特性曲线的绘制方法是选择几个恰当的工况点，然后对这些点进行曲线拟合，采用不同的拟合方法得出的曲线也不尽相同。这里采用最小二乘法来拟合煤耗特性曲线。当采用二项式拟合时，由于高阶导数对余项的影响较大导致误差很大。因此，本文采用二次多项式来对煤耗特性曲线进行拟合。

以下为监测某电厂的三台328.5 MW机组得出的实际运行数据，如表1所示。

表1 机组负荷能耗表

根据最小二乘法，对表1数据进行拟合，得到下列煤耗特性方程及曲线图（分别如图1、图2所示）。

1#机组煤耗特性方程为：

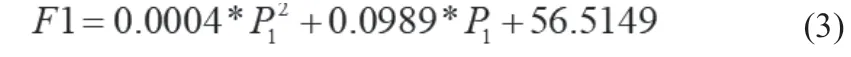
2#机组煤耗特性方程为：

2 等微增率法的应用

2.1 负荷优化算法数学模型

要想实现厂级负荷优化算法的设计，就要在符合电网中调给定要求的情况下让系统的煤炭消耗量达到理想中的最低值。本文选用供电煤耗作为目标函数的参数。

2.2 等微增率法

等微增率法和协调方程式法是以古典变微分原理为基础，对纯火电机组负荷分配及其最优化的经济运行有重要的作用。

已知某时段机组的组合固定，根据等微增率法的具体解法进行机组组合的可行性检查，它主要包含：火电机组开始频率、火电机组负荷承载时启停次数及其每次时间的长短、影响火电机组的速度因素、火电机组旋转时功率大小的影响因素等，通过以上内容对火电机组进行负荷分配应该是最优的，这样的话应用等位增率法只能对某一特定的火电级机组的负荷优化分配。

机组通过设置约束条件进行相应的可行性检查，在存在机组越限情况下，通过等微增率法的逐次逼近可以得到最优解。相应煤炭的消耗量变化是由负荷的微小变动来实现的，而这一微小变动可通过任一微增率来反映。通过微增率的相对大小的变换，来调整负荷使目标函数值趋近于最小值。

图1 1#机组煤耗特性曲线

图2 2#机组煤耗特性曲线

图3 负荷分配遗传算法的收敛曲线

2.3 等微增率法的特点

在古典变分原理的基础上形成的等微增率法是简单方便、清晰明了的。但该算法也有一定的缺点，其没有办法保证火电机机组的煤耗量为最小，有的工厂为了获得更多的利益不择手段，没能精确地记录各台电机的具体煤耗量，导致拟合的曲线存在误差。只有准确无误的数据，才能保证曲线的正确性，才能凸显出等微增量法是最经济的方法。若未将等微增率特性考虑在内，结果并不一定实惠。在实际生产应用中，一定要根据实际数据来求解。在现实生活生产中难免会出现多项式拟合的曲线，它的多项式系数为负数的情况，在处理现实生产的数据过程中，煤耗特性曲线可利用双曲线函数来拟合。

3 遗传算法的应用

3.1 遗传算法

1962年，美国Michigan大学的John Holland提出了监控程序的定义,也就是说利用群体进化理论来模拟适应性的系统的思想。1967年,Holland的学生J.D.Bagley第一次在他的博士论文中提出“遗传算法(GA)”这个词语，逐渐演变成复制、变异、交叉、倒位、显性等遗传算子，双倍体的编码方法也应用在个体编码。

本课题中要求的限制条件不多，遗传算法对初始种群的产生也没有具体的要求，因此可以采用最简单的随机生成的方式生成随机的初始种群。初始种群中个体的数目为M，表示为种群中机组的组数。初始种群中个体的数目直接决定了遗传算法的准确性和效率，当初始种群的个体数目过少时，虽费时较少但容易出现过早成熟的问题，不具有一定的准确性，而当初始种群的个体数目过多时，我们可以经过多次的遗传算法运算来得到一个准确的结果，但需要大量耗时来运算，不具有效率性。从整体的执行效果和时间来分析，将M的初值设定为35较为合适，可以达到理想的效果。采用适用度比例法（轮盘赌法），种群中每一个个体被选择的概率与其适应度成比例关系，适应度强则被选择的概率越大，不强则易被淘汰，从而实现遗传算法。

3.2 算例

遗传算法是把概率作为一种工具来引导其朝着搜索空间的更优化的解区域移动的过程。所以在算法中遗传过程的一些参数，例如：遗传代数、遗传概率、子串长度等都会影响到程序的结果。即使所有的参数相同，由于遗传算法不是采用确定性规则，而是采用概率的变迁规则来指导它的搜索方向，所以每次得到的结果会有一定的误差。

在本算例中，参与优化组合分配的系统为10机系统，如果组合给定，假如组合为 0000011111，系统负荷为2000 MW，用本遗传算法计算可得到分配结果如表2，总煤耗量为4245t/h。

表2 分配结果

随着迭代次数的增加，系统的煤耗量逐渐接近于最优值，其算法的收敛曲线如图3所示。

结论：本文分析了国内外负荷优化理论的研究状况，结合火电厂实际运行情况，考虑机组的启停次数及造成的损失，并且以供电煤耗为目标函数对煤耗特性曲线进行拟合，采用无回放余数随机选择操作策略的遗传算法对特定时间段的某些机组进行负荷分配，以获取最好的经济效益。本文对火力发电厂的机组负荷分配进行了初步的讨论研究，文中提及的算法在实际运用中还需完善。而对于负荷分配，如何与实时系统相连接，从而得到完整的实时负荷分配系统是今后进一步研究的方向。