并列双圆柱绕流的动力学模态分解

袁 猛，张新玉，柳贡民，张文平

（哈尔滨工程大学动力与能源工程学院，哈尔滨150001）

0 引 言

计算机性能的提高和快速算法的研发使得流场的研究和分析变得更加简便快捷，将复杂的流场结构分解为模态结构的分析方法越来越多地用在流场分析和稳定性判断等问题中。在获取流场模态信息方面，基于流场数据的算法比基于控制方程的算法具有更高的效率[1]。传统的本征正交分解方法可以用于获取流动结构，但是对于求解可压缩流动的模态信息有一定困难。在2009年美国物理学会会议上Schmid[2]首次提出了DMD方法，并以氦气射流为例进行了验证，在之后的研究中又进一步说明了该方法在处理仿真和试验数据中的作用。DMD方法在一定程度上弥补了本征正交分解方法的不足。

DMD 方法自从被提出后的十年时间里，已经被广泛地应用于多个领域的分析研究中，例如金融[3-4]、能源[5-6]、人工智能[7]、医疗[8]等。在流体力学的研究方面，Zhu等[9]利用DMD 方法提取了涡轮增压器蜗壳在设计工况和温和喘振条件下的主导的流动结构和对应的频率，动态展示了冲击条件下蜗壳内的流动发展过程。Sarkar 等[10]研究了纳米流体通过方柱时混合对流的稳定性，发现铜-水纳米流体的高频模态比氧化铝-水纳米流体具有更加小的尺度结构。Muld 等[11]利用动模态分解提取了高速列车周围的流结构。DMD方法具有数据量大、噪声和误差影响精度的问题。在优化和改善DMD方法的相关研究方面，Brunton 等[12]对DMD 方法进行了改进来消除潜在的动力学和驱动之间的影响，以便得到更加准确的输入和输出数据之间的关系。Duke等[13]进行了DMD 方法的误差分析，提出了减小误差的方法。国内也有一些学者对DMD进行了应用研究[14-15]，但总体来讲，关于动力学模态分解研究的文献资料还比较少。

本文首先对并列双圆柱绕流卡门涡街的形成和发展过程进行非稳态数值仿真；然后使用DMD 方法对仿真所得的涡量数据进行稳定性分析，得到各阶模态以及对应模态的频率和振幅；再利用模态数据还原了涡量场并预测快照之外时刻的流场，验证动态模态分解方法在预测流场方面的作用；最后对比不同奇异值截断阶数下的预测效果。

1 动力学模态分解方法

获取动力学降阶模型可以采取两种方法，分别是伴随矩阵法和近似矩阵法，而后者比前者具有更好的鲁棒性[16]。关于DMD 的原理推导，可以参见文献[17]。本文的分析采用近似矩阵法，在此简要叙述该方法的计算过程。

设在初始时刻系统的观测值或者实验值为一个列向量x1，其为初始时刻的快照，列向量的元素中包含了系统不同空间位置的同一个物理量的值，之后每隔相等的时间步长Δt进行一次数据采样，直到第k × Δt时刻停止，得到共计k组数据（即k组快照）构成数据集合，记为

假设当k增大到一定值时，上述数据集合构成的矩阵的秩不再变化，即第k + 1个观测值可以由前面的k个观测值线性表示，则可以用矩阵A将两个相邻的快照联系起来：

对于试验或仿真过程中的所有k组采样数据，有如下关系：

式中，W 为A'的特征向量构成的矩阵，Λ 为对角矩阵，其对角线元素由A'的特征值构成。使用A'的特征值和特征向量可以得到DMD模态：

式（8）中Φ 的列向量φi即为DMD 模态，模态对应的特征值就是Λ 的对角线上的元素λi，ln(λi)/Δt的实部是模态的衰减率（放大率），虚部表示模态出现的频率。利用DMD 模态，由式（9）重构或预测t + Δt时刻的数据快照[17]：

式中，bi为第i 个模态的振幅，b 为由元素bi构成的仅包含一列元素的矩阵，b 可以根据Φb = x1得到。也就是对于第k个数据快照，用n阶模态可以表示为

式中，φi为由式（8）得到的矩阵Φ的第i个列向量，λi为由式（7）计算得到的Λ的对角线上的元素。

2 双圆柱绕流流场数值仿真

建立双圆柱模型并使用流体动力学计算软件Fluent进行仿真。计算域模型网格如图1所示，模型总高为20 m，总宽度为50 m。两圆柱直径均为1 m，圆心纵向间距为2.2 m，圆柱模型的圆心距离左侧入口边界为20 m。

模型入口边界条件为速度入口，流速为4 m/s。出口设置为压力出口，工作流体为空气，对应的物性参数均按照0 ℃、一个大气压力下选取。监测量为出口压力和圆柱面上的升力和阻力。非稳态计算时间步长为0.01 s，计算5 000 个时间步后的升力和阻力随计算时间的变化，如图2 所示，达到稳定时的涡量分布如图3 所示。从图3 可以看出，在当前圆柱间距和参数设置下圆柱下游产生的涡街方向一致，属于同步同相模式，与文献[18]中所述吻合，说明了仿真结果的正确性。

图1 数值仿真二维模型图Fig.1 Numerical simulation of two-dimensional model diagram

图2 圆柱受到的升力阻力随迭代次数的变化（红：上方圆柱；蓝：下方圆柱）Fig.2 The change of lift and drag force of the two cylinders with the number of iteration (Red:upper cylinder;Blue:lower one)

从图2 中可以看出：两圆柱的升力、阻力变化周期保持一致，约为1.25 s；曲线波动规律较为相似，均在19 s 左右突然产生了明显波动；在流动的初始阶段，两个圆柱受到的升力作用相差半个周期，而在19 s 之后，两个圆柱受到升力作用的时刻保持同步，阻力作用的变化规律与之相反。根据升阻力曲线的变化规律，将双圆柱绕流的流动过程分为不稳定周期阶段和稳定周期阶段（图2（b）中绘制了阶段分界线），分阶段描述有助于更加清楚地分析圆柱绕流的演化。

图3 50 s时涡量分布图Fig.3 Vorticity distribution map in 50 s

3 DMD计算分析

3.1 动态模态分析

在不稳定的周期阶段取初始的0～5 s 时间跨度作为DMD 分析的快照数据，共计500 个快照，如图2（a）中快照空间所示。图4（a）为特征值的实部和虚部在单位圆的分布，位于特征圆外的点共有17个（绿色标识），分别对应8对共轭模态和一个主导模态，其均为不稳定模态。其余特征值均位于单位元内部或圆上，属于稳定模态和周期性模态。值得注意的是，由于计算机舍入误差的影响，严格意义上，到圆心距离完全等于半径的点并不存在，此问题在稳定的周期阶段的分析中也会遇到，因此特征圆的方法分析仅为定性分析判断模态稳定性的判据。图4（b）中是在稳定的周期阶段时间跨度20～25 s 下同样取500 个快照作为分析数据得到的特征值圆，从图中可以看出几乎所有的特征值都落在圆内和圆上，而与原点的距离小于1.001的特征值个数为0，即除去舍入误差的影响以后没有特征值落在单位圆外部，此时几乎所有模态都属于稳定模态或周期性模态。图4（b）与图4（a）相比，稳定性模态较少，而周期性模态较多，几乎所有特征值都落在单位圆上，属于稳定的极限环阶段。

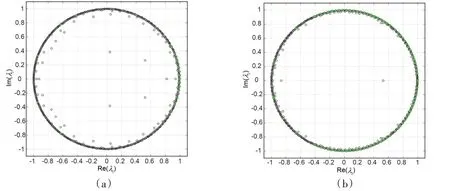
图4 两个流动阶段的特征值圆Fig.4 The distribution of real and imaginary parts of eigenvalues in the unit element

根据Xk-11矩阵奇异值的变化，使用硬阈值方法作为判据截断奇异值[17]。在不稳定的周期阶段的计算中丢弃21阶之后的奇异值，按照振幅从大到小对前五阶模态从A-E进行编号，模态参数如表1所示，振幅和放大率的关系如图5所示。

表1 不稳定周期阶段按振幅排列的前5个模态参数Tab.1 Mode parameters of the first five modes arranged by amplitude in unstable period

图5 不稳定的周期阶段放大率与振幅的关系Fig.5 Magnification in relation to amplitude in unstable period

由图5 可以看到，A 点的振幅远大于其他模态的振幅，即A 点对应的流场能量相对于其他模态较高，但是其对应的模态衰减率也最大，因此该模态是逐渐衰减的模态，模态能量也会逐渐降低，其频率为0，说明其还属于发展阶段的不稳定模态，该模态对各个不同时刻的流场结构贡献相同。B 点对应的模态能量强度较大，且放大率为-1.27，其频率为0，其能量强度呈现逐渐减小的趋势，也属于发展中的模态。从频率上看，C 和D 两个点对应的模态对各个流场的作用是有差异的，D 点对应的模态对不同时刻的流场影响大于C 点对应的模态。另外，就模态本身而言，两个模态能量相差不大，但是D 点对应的模态变化要快于C 点。E 点的振幅相对于其他模态较大，其衰减率最小且频率为0，因此可以判断E 点对应的是平均流场状态，即静态模态，如图6 所示。对稳定的周期阶段进行DMD 分析，前五阶模态参数如表2所示。

图6 E点对应的模态云图Fig.6 The modal cloud diagram corresponding to Point E

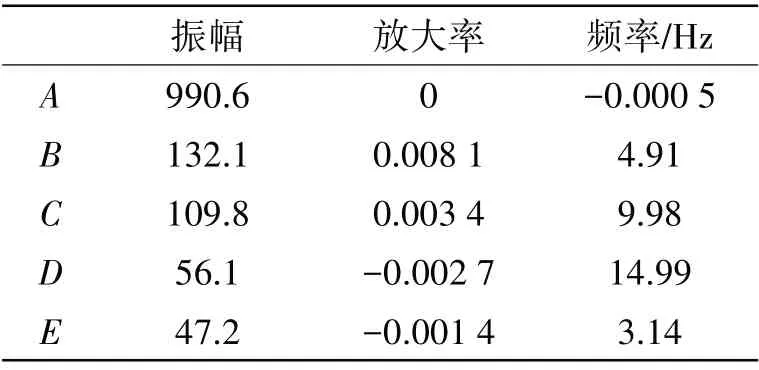
表2 稳定周期阶段按振幅排列的前5个模态参数Tab.2 Mode parameter of the first five modes arranged by amplitude in stable period

振幅和放大率的关系如图7 所示。从图中可以看出，A 点对应的模态系数幅值最大，且其放大率为0，频率极小，模态系数幅值基本不变且对各时刻流场的作用基本相同，其对应的是流场的平均状态，对应的模态云图如图8所示。B点和C点对应的模态放大率为正值，幅值较大，且其模态系数幅值还有继续增大的趋势，属于发散的模态。D点和E点对应的模态放大率不大，模态幅值较大，其反应了流场随时间的变化特征。对比表1和表2处于两个阶段的模态放大率，可以看出稳定的周期阶段放大率比不稳定的周期阶段小一个数量级以上，说明不稳定的周期阶段流场稳定性较差。下文将利用本节提取的模态信息对原始的涡量场进行重构和预测，以验证DMD 方法提取流场特征的效果，研究所提取的模态用于预测涡量场发展的作用。

图7 稳定的周期阶段放大率与振幅的关系Fig.7 Magnification in relation to amplitude in stable period

图8 A点对应的模态云图Fig.8 The modal cloud diagram corresponding to Point A

3.2 流场重构与预测

对图2（b）中三角标示对应的流场时刻，即4s、8s 和16 s 处进行涡量场的还原及预测，其中8 s 和16 s 时刻的涡量数据没有包含在快照中，故属于涡量场的预测过程。涡量场云图还原及预测结果如图9所示。由图中可以看出，对于快照空间时刻内的涡量场，使用动模态分解方法已经能够捕捉关键的流场特征并进行流场还原，原始流场与还原流场高度吻合。对于“未来时刻”的流场，从图9（e）中可以看出，用模态信息进行预测得到的涡量场还是按照原来的发展规律向后方不断变化，但是对于实际涡量已由原来的涡街对称的形式变化为同步形式，这说明对于流型转换时的流场特征，前面的500个快照显然没有捕捉到关键的流场变化特征，这是由数据快照提供的流场特征不足导致的。图2（b）中矩形标示的时刻对应的流场处于稳定的周期阶段，对该三个时刻的涡量场进行还原及预测，结果如图10所示。从图中可以看出，尽管只选取了7个奇异值对原始数据矩阵进行近似，但是其对快照内流场的还原效果以及对流场发展的预测效果良好，丢失的流场特征较少。

图9 不稳定的周期阶段模态预测涡量场与真实涡量场对比Fig.9 Comparison between the prediction vorticity field and the real field in unstable period

图10 稳定的周期阶段模态预测涡量场与真实涡量场对比Fig.10 Comparison between the prediction vorticity field and the real vorticity field in stable period

3.3 奇异值截断阶数对流场还原效果的影响

奇异值的选择个数会影响流场还原和预测的精度，对不稳定的周期阶段，奇异值的截断个数分别为7、21、50、130 时的涡量值变化进行对比，图11 为位于上方的圆柱下游方向，距离圆柱圆心1.5 m 处的采样点的涡量值变化的真实值与还原值对比。

图11 采样点在不同奇异值截断阶数的涡量还原值与真实值对比（红线对应真实值，蓝线对应还原值）Fig.11 Prediction vorticity and the real vorticity at Point M under different truncation orders (Red line: real values,Blue line:prediction data)

从图11可以看出，截断个数为7，即取前7个主要的奇异值时，还原的值与原始值差距较大，DMD方法的还原结果与采样点涡量真实值的变化周期一致，但是同步性较差。截断个数取21 阶时，虽然在数值准确性上稍差，但是两曲线的变化完全同步，此时通过DMD 方法的还原结果可以预测快照外的近似值以及变化规律。当截断个数为50时，虽然奇异值取的较多，用于还原流场的模态个数增加，但是可能是引入了不必要的干扰模态，导致预测值周期性虽然与原始流场一致，但预测值的变化幅值整体呈发散趋势。当取130个奇异值时，预测值与原始值在1 600个快照时刻以内都高度吻合。对比图11 的四个图可以看出，在第1 600 个快照时刻，涡量还原值与真实值两条曲线的周期始终不能一致，其与奇异值截断大小无关。真实的涡量值在第1 600 个快照时刻发生了剧烈变化，此时为并列双圆柱绕流流型的转换阶段，由于该阶段没有在快照空间内，因此单纯增加奇异值截断参数也未能捕捉到此时刻的流场特征，导致对该时刻的涡量场还原效果较差。

4 结 论

本文利用DMD 方法对仿真得到的双圆柱绕流流场的涡量数据进行了分析，研究了不同流动阶段的绕流流场的稳定性和奇异值截断阶数对于DMD预测效果的影响，得出以下主要结论：

（1）DMD方法可以准确提取双圆柱绕流流动过程中的流场特征和各主导模态。

（2）对于圆柱绕流稳定的周期阶段，流场分布较为规律，流场还原所需模态较少；对于不稳定的周期阶段，判断稳定性需要更多的模态，即对于发展中的流场，重构和预测流场所需模态更多，而且效果较差。

（3）增加奇异值的截断阶数并不能始终对预测效果起到积极作用，需要合理判断来避免使用对流场特征的贡献呈现消极作用的模态进行数据还原和预测。